Compact Representations of Separable Graphs From a paper

Compact Representations of Separable Graphs From a paper of the same title submitted to SODA by: Dan Blandford and Guy Blelloch and Ian Kash

Standard Graph Representations • Standard Adjacency List - |V| + 2|E| words = O(|E|lg|V|) bits - |V| + |E| words if stored as an array • For arbitrary graphs, lower bound is O(|E| lg (|V|2/|E|)) bits, which adjacency list meets for sparse graphs, i. e. |E| = O(|V|)

Representations for Planar Graphs that use O(|V|) bits • No Query Support - Turan [1984], First to come up with an O(|V|) bit compression scheme - Keeler and Westbrook [1995], Improved constants - Deo and Litow [1998], First use of separators - He, Kao and Lu [2000], Optimal high order term • Query Support - Jacobson [1989], O( lg |V|) adjacency queries - Munro and Raman [1997], O(1) adjacency queries - Based on page embeddings and balanced parentheses, so not generally applicable

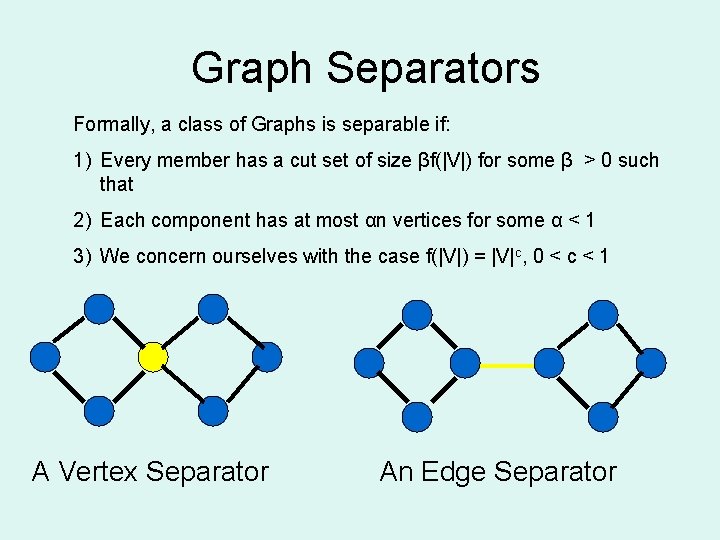
Graph Separators Formally, a class of Graphs is separable if: 1) Every member has a cut set of size βf(|V|) for some β > 0 such that 2) Each component has at most αn vertices for some α < 1 3) We concern ourselves with the case f(|V|) = |V|c, 0 < c < 1 A Vertex Separator An Edge Separator

Classes of Graphs With Small Separators Many Interesting and Useful Classes - Planar (and all bounded genus) - Telephone / Power / Road networks - 3 D Meshes (Miller et al. [1997]) - Link Structure of Web

Results Theory for both edge and vertex separators • Compress Graphs to O(|V|) bits • Meets Lower Bound for Query Times - Degree Queries – O(1) - Adjacency Queries – O(1) - Neighbor Queries – O(D), D = Degree Implementation for edge separators

Main Ideas 1) Build separator tree 2) Order based on tree 3) Compress using difference encoded adjacency table 4) Use root find tree* * Vertex separators only

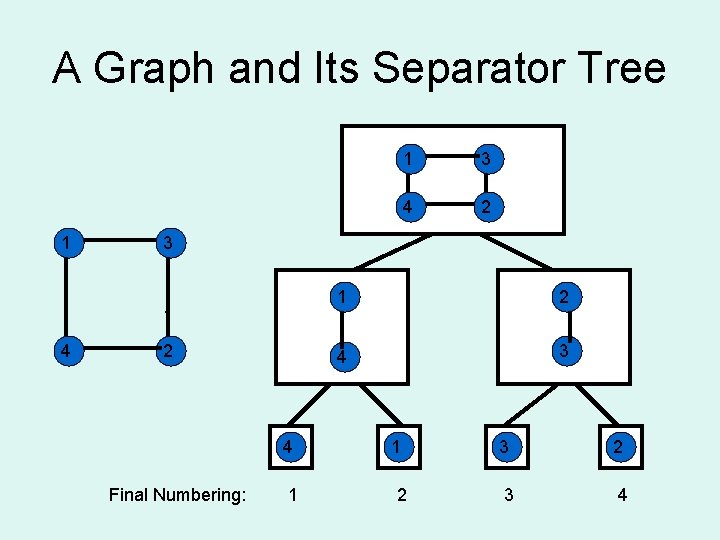
A Graph and Its Separator Tree 1 3 4 2 3 1 4 1 2 4 Final Numbering: 1 11 2 4 3 1 2 3 4

Difference Coded Adjacency Table • Instead of storing absolute numbers, store offsets • i. e. : 1, 1, 3, 2, 1 instead of 1, 2, 5, 7, 8 • Makes numbers stored smaller • By itself, it offers no advantage

Gamma Code • Variable length encoding with 2 parts • 1 st Part: Unary code of length of 2 nd part • 2 nd Part: Number in binary • Encoding n takes 2└lg(n+1)┘=O(lg(n)) bits • There are other codes with similar properties (Ex: Delta Code) Number 1 2 3 4 5 6 7 8 9 Encoding 00 01 1000 1001 1010 1011 110000 110001 110010

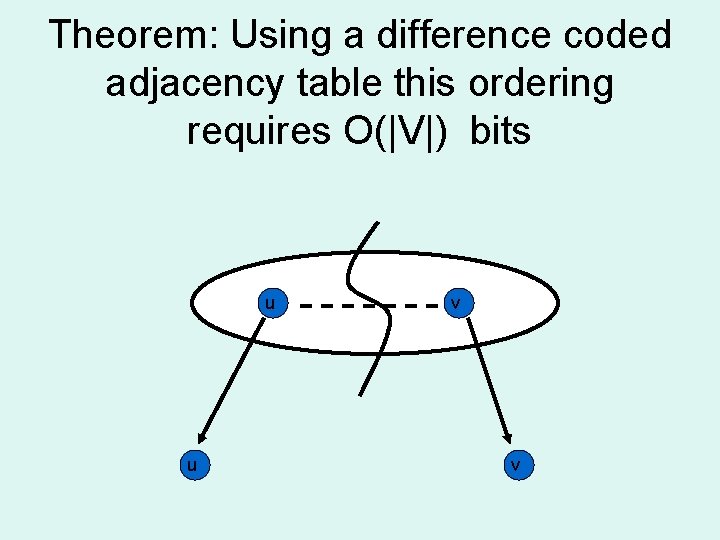
Theorem: Using a difference coded adjacency table this ordering requires O(|V|) bits u u v v

Sketch of Proof • The maximum distance between the numbers of u and v is the number of vertices in their Least Common Ancestor in the separator tree (n) • With Gamma Code this takes O(lg(n)) bits • Recurrence: S(n) ≤ 2 S(. 5 n) + O(nc lg(n)) • As a geometrically decreasing recurrence, this solves to S(|V|) = O(|V|)

Decoding Vertex i in O(1) time Pointer to Vertex i-1 Degree Edge 1 Edge 2 Edge 3 Vertex i+1 • We can decode lg(|V|) bits at a time through table lookup • An Edge Takes O(lg(|V|)) bits, and the degree of a vertex for a graph with good edge separators is constant • We decode the entire vertex using a constant number of table lookups

Problem! • This assumes we have a pointer to vertex i • Requires |V| pointers of lg |V| bits each = O(|V| lg|V|), but the graph uses only O(|V|) • Can afford a pointer to a BLOCK of lg |V| vertices O(lg |V| * |V| / lg |V|) = O(|V|) • Can afford a pointer to a SUBBLOCK of at least k lg |V| bits • Can afford extra 2 lg |V| bits per block

Getting a Pointer to Vertex i in O(1) Pointer to Block (calculate as i / lg (|V|) Previous Block 100110 Pointer to Block Pointer to Offsets Next Block Flags to determine subblocks. A 1 is the start of a subblock Prev. Subblocks Offset for 2 nd Subblock Offset for 3 rd Subblock The Process: 1) Calculate block number 2) Identify subblock number 3) Get subblock offset 4) Add offset to pointer 5) Decode any Previous vertices (at most k lg |V| bits) Next Subblocks

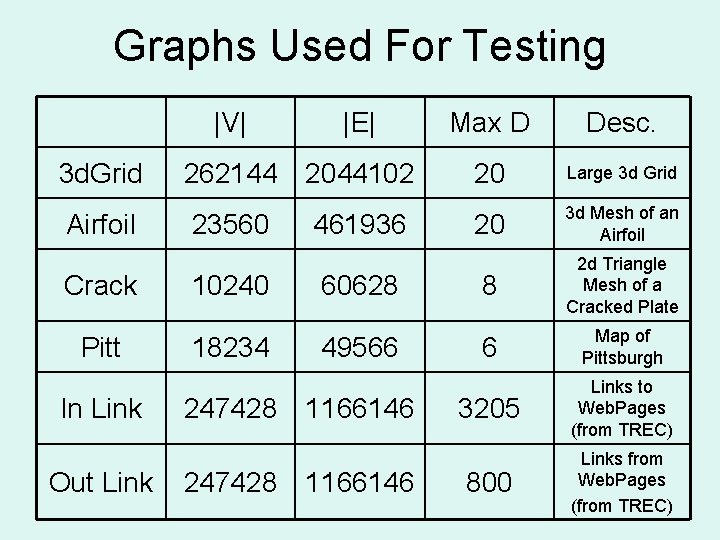
Graphs Used For Testing 3 d. Grid Airfoil Crack Pitt In Link Out Link |V| |E| Max D Desc. 262144 2044102 20 Large 3 d Grid 20 3 d Mesh of an Airfoil 8 2 d Triangle Mesh of a Cracked Plate 6 Map of Pittsburgh 3205 Links to Web. Pages (from TREC) 800 Links from Web. Pages (from TREC) 23560 10240 18234 247428 461936 60628 49566 1166146

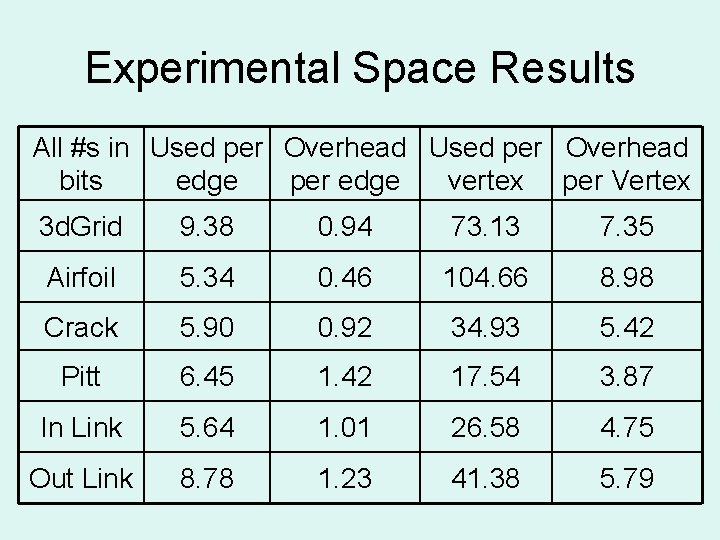
Experimental Space Results All #s in Used per Overhead bits edge per edge vertex per Vertex 3 d. Grid 9. 38 0. 94 73. 13 7. 35 Airfoil 5. 34 0. 46 104. 66 8. 98 Crack 5. 90 0. 92 34. 93 5. 42 Pitt 6. 45 1. 42 17. 54 3. 87 In Link 5. 64 1. 01 26. 58 4. 75 Out Link 8. 78 1. 23 41. 38 5. 79

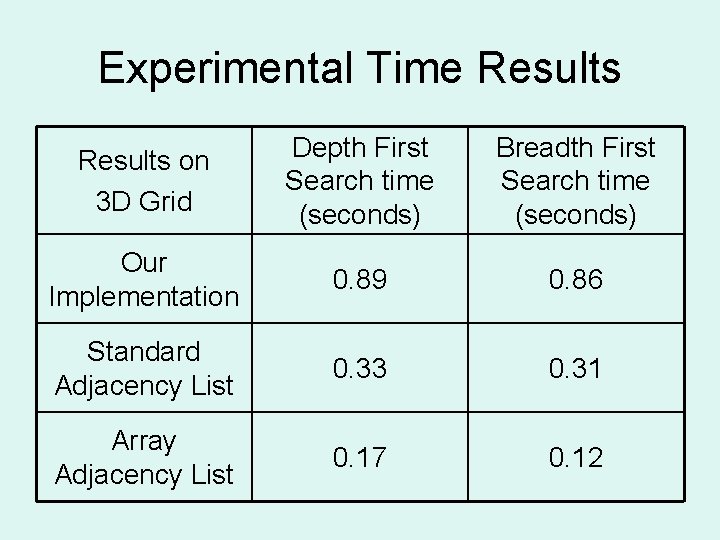
Experimental Time Results on 3 D Grid Depth First Search time (seconds) Breadth First Search time (seconds) Our Implementation 0. 89 0. 86 Standard Adjacency List 0. 33 0. 31 Array Adjacency List 0. 17 0. 12

Conclusions • Our Method uses O(|V|) bits to compress a graph with good separators • On test graphs with good separators, it used less than 12 bits per edge, including overhead • It meets the lower bounds for queries • With unoptimized table lookup it takes 3 times as long to search as a standard adjacency list representation and 6 times as long as an array based adjacency list

Future Work • • • Test decoding speed on more graphs Optimize decoding Allow addition / deletion of edges More Efficient Separator Generator Implement Vertex Separators

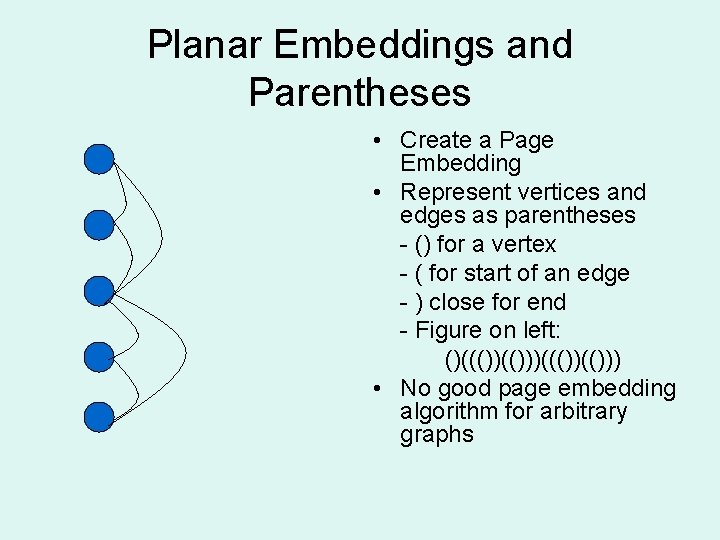
Planar Embeddings and Parentheses • Create a Page Embedding • Represent vertices and edges as parentheses - () for a vertex - ( for start of an edge - ) close for end - Figure on left: ()((())(())) • No good page embedding algorithm for arbitrary graphs