Compact Data Structures and Applications Gil Einziger and

Compact Data Structures and Applications Gil Einziger and Roy Friedman Technion, Haifa

Approximate Set Membership • The problem: – Maintain enough state to approximately answer set membership queries. (add/query). • Things to consider: – False positive probability. – No false negatives! – A tradeoff between space and the false positive probability. Bloom filters are the classical example.

Application Example: Black List • • Client: Server: Mission: Challenge: Web browser Let’s say Google’s data center. Check if each accessed URL is part of the black list. The black list is too big to fit in memory. Trivial Solution: access data center for each URL Approximate Set: Access data center only in case of a positive answer. (must access it as the answer may be wrong) Your Computer But… there are no false negatives! Therefore every site that tests negative is not on the list and we do not have to contact the datacenter. Data Center

Bloom Filters • An array BF of m bits and k hash functions {h 1, …, hk} over the domain [0, …, m-1] • Adding an object obj to the Bloom filter is done by computing h 1(obj), …, hk(obj) and setting the corresponding bits in the Bloom filter. • Checking for set membership for an object cand is done by computing h 1(cand), …, hk(cand) and verifying that all corresponding bits are set BF= 1 √ h 1(o 1)=0, h 2(o 1)=7, h 3(o 1)=5 × h 1(o 2)=0, h 2(o 2)=7, h 3(o 2)=4 1 m=11, k=3, 1

Approximate Counting • Multiset: Instead of a query – ‘estimate’ operation “How many times the item was added before? ” • Things to consider: – False positives – No false negatives • we only get over approximation! – A tradeoff between space and accuracy Typically solved with Bloom filter extensions – like Spectral Bloom filter, Count Min Sketch, Multi Stage Filters and many more.

Counting with Bloom Filter • A vector of counters (instead of bits) • A counting Bloom filter supports the operations: – Increment • Increment by 1 all entries that correspond to the results of the k hash functions – Decrement • Decrement by 1 all entries that correspond to the results of the k hash functions – Estimate (instead of get) • Return the minimal value of all corresponding entries CBF= 43 k=3, h 1(o 1)=0, h 2(o 1)=7, h 3(o 1)=5 89 m=11 67 Estimate(o 1)=4

Some Applications • • • Google Chrome Google Big. Table Apache Hadoop Facebook’s (Apache) Casandra Venti (archive system) Cache Admission Policy – And many more…

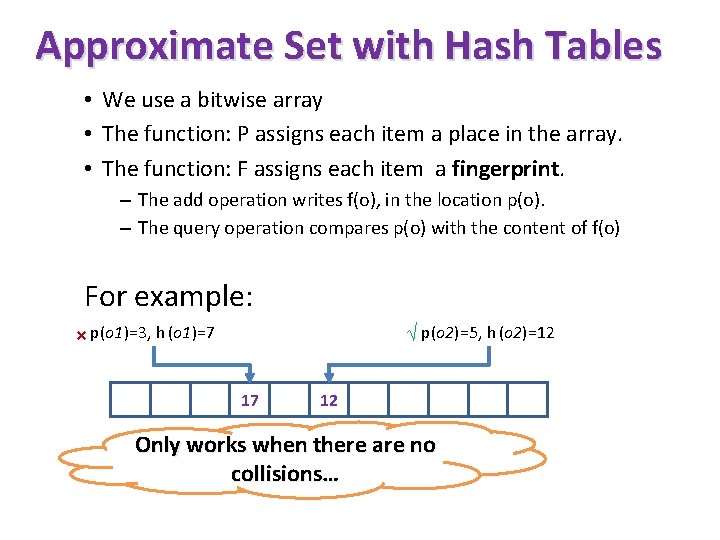
Approximate Set with Hash Tables • We use a bitwise array • The function: P assigns each item a place in the array. • The function: F assigns each item a fingerprint. – The add operation writes f(o), in the location p(o). – The query operation compares p(o) with the content of f(o) For example: √ p(o 2)=5, h (o 2)=12 × p(o 1)=3, h (o 1)=7 17 12 Only works when there are no collisions…

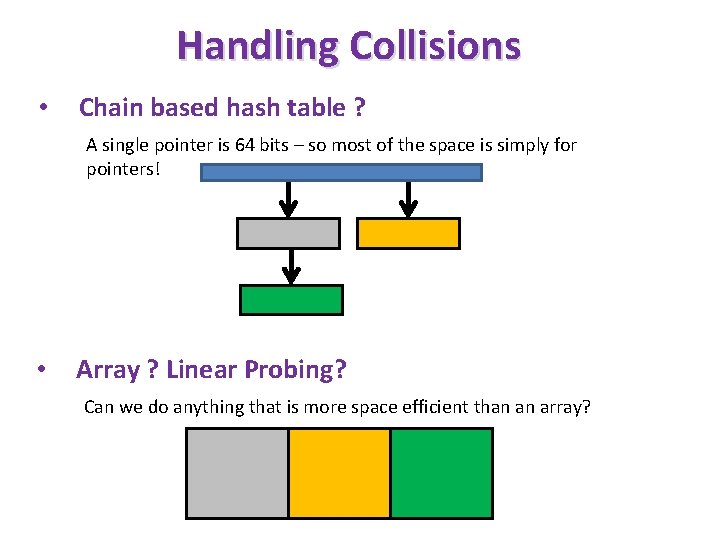
Handling Collisions • Chain based hash table ? A single pointer is 64 bits – so most of the space is simply for pointers! • Array ? Linear Probing? Can we do anything that is more space efficient than an array?

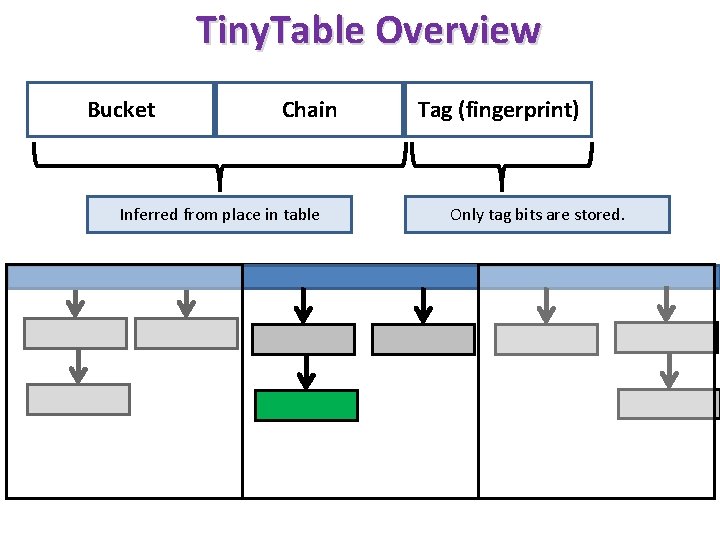
Tiny. Table Overview Bucket Chain Inferred from place in table Tag (fingerprint) Only tag bits are stored.

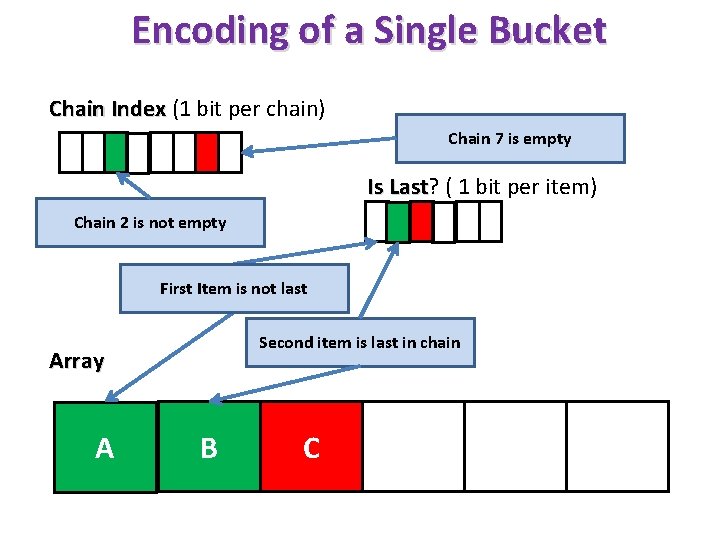
Encoding of a Single Bucket Chain Index (1 bit per chain) Chain 7 is empty Is Last? Last ( 1 bit per item) Chain 2 is not empty First Item is not last Second item is last in chain Array A B C

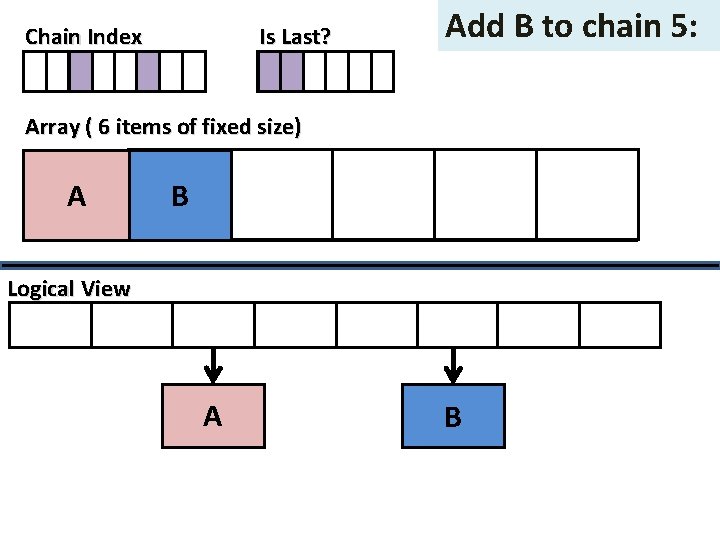
Is Last? Chain Index Add B to chain 5: Array ( 6 items of fixed size) A B Logical View A B

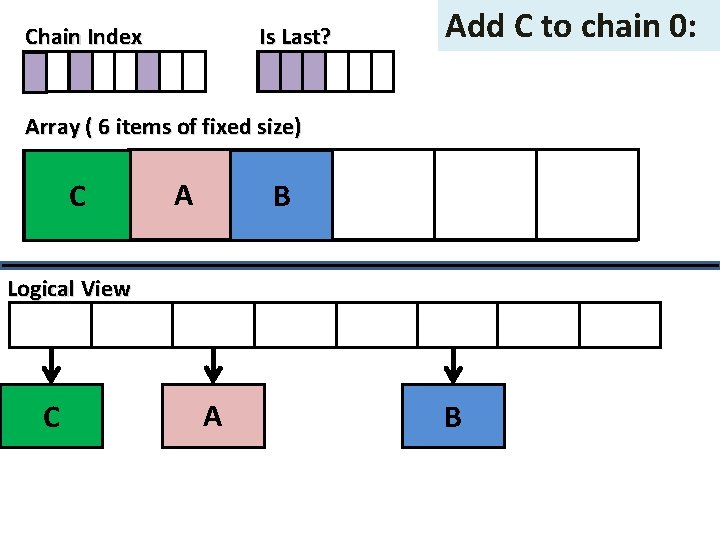
Is Last? Chain Index Add C to chain 0: Array ( 6 items of fixed size) C A BA B Logical View C A B

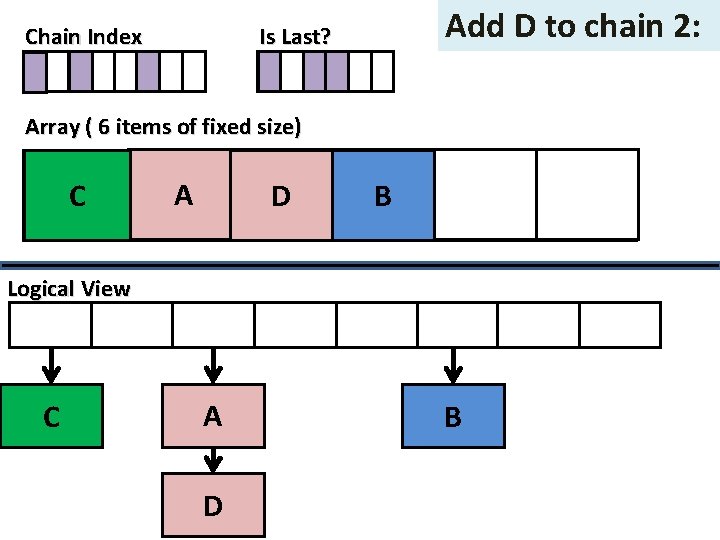
Add D to chain 2: Is Last? Chain Index Array ( 6 items of fixed size) C A BA D B B Logical View C A D B

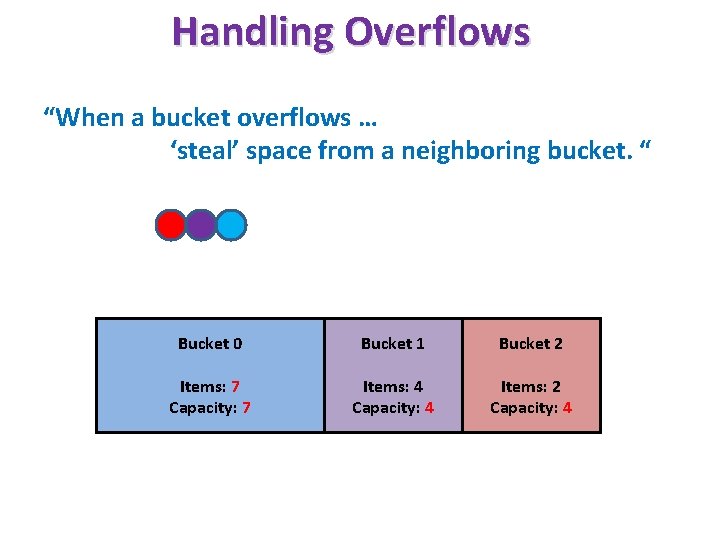
Handling Overflows “When a bucket overflows … ‘steal’ space from a neighboring bucket. “ Bucket 000 Bucket 11 1 Bucket 22 Items: 4 567 Capacity: 567 Items: 44 4 Capacity: 54 4 Items: 22 Capacity: 54

Performance Tradeoff •

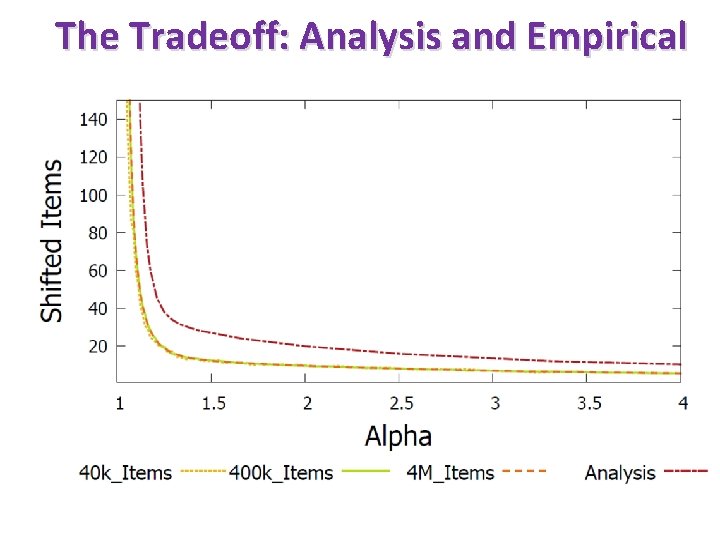
The Tradeoff: Analysis and Empirical

Time for 1 million operations (seconds) Alpha = 1. 2 Alpha = 1. 1 Alpha = 1. 025 Query is over 10 times faster than in Bloom filter, regardless of alpha. Update Speed depends on alpha – and can be similar to that of Bloom filters.

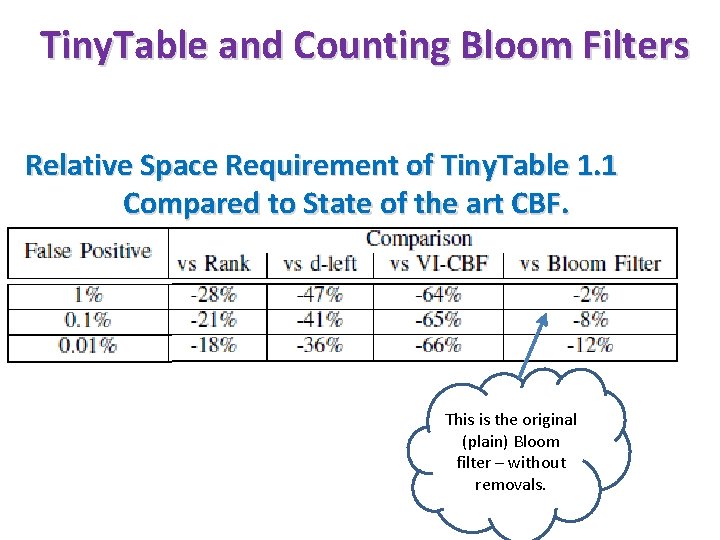
Tiny. Table and Counting Bloom Filters Relative Space Requirement of Tiny. Table 1. 1 Compared to State of the art CBF. This is the original (plain) Bloom filter – without removals.

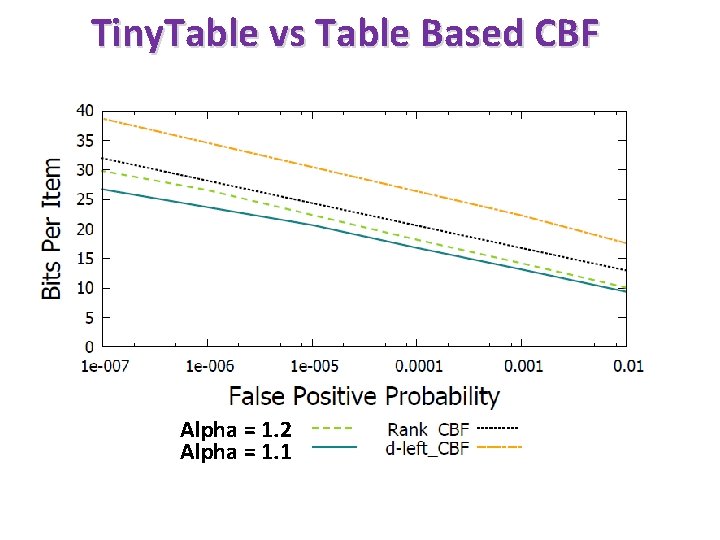
Tiny. Table vs Table Based CBF Alpha = 1. 2 Alpha = 1. 1

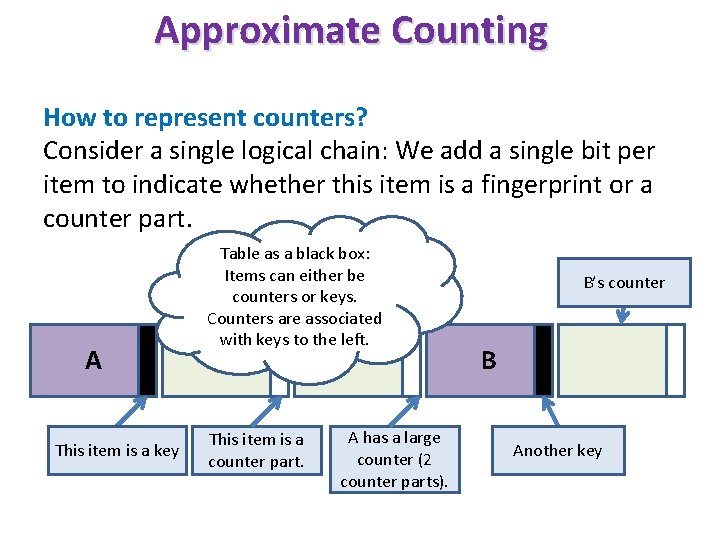
Approximate Counting How to represent counters? Consider a single logical chain: We add a single bit per item to indicate whether this item is a fingerprint or a counter part. A This item is a key Table as a black box: Items can either be counters or keys. Counters are associated with keys to the left. This item is a counter part. A has a large counter (2 counter parts). B’s counter B Another key

Summery: Tiny. Table • Query is always very fast It is based on efficient bitwise operations and very memory local. • Update time depends on memory density, density denser table = slower update. • Full support of additions, removals and counting. • Many attractive configurations! Can be made smaller than Bloom filters with reasonable (better) performance.

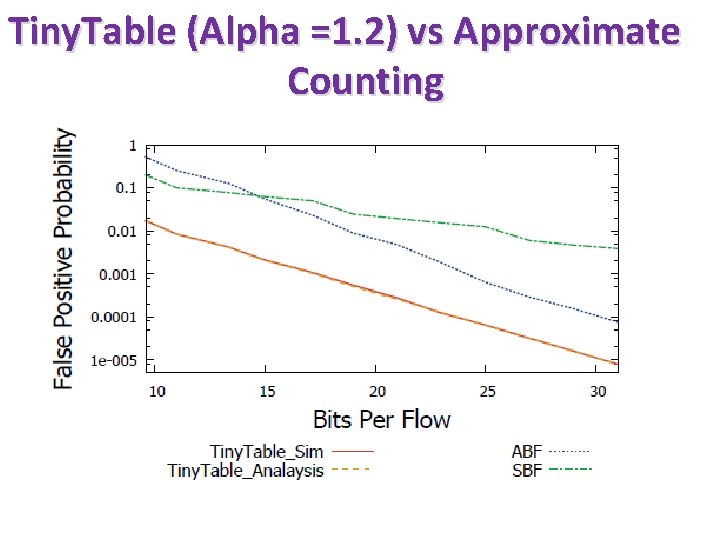
Tiny. Table (Alpha =1. 2) vs Approximate Counting

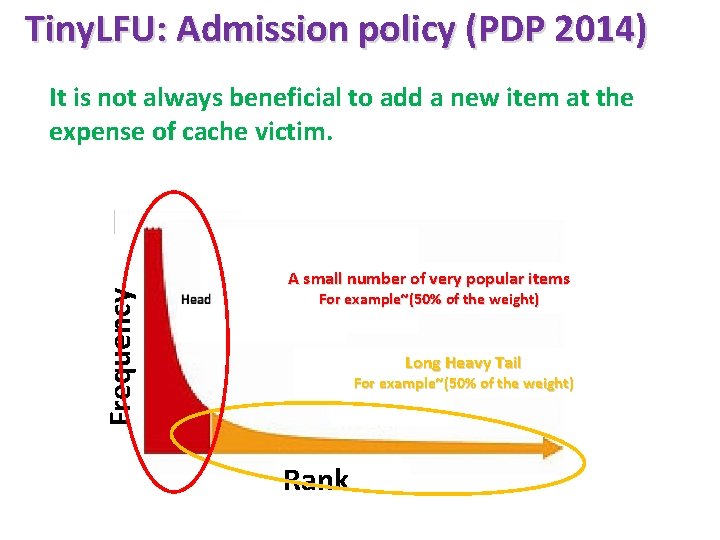
Tiny. LFU: Admission policy (PDP 2014) Frequency It is not always beneficial to add a new item at the expense of cache victim. A small number of very popular items For example~(50% of the weight) Long Heavy Tail For example~(50% of the weight) Rank

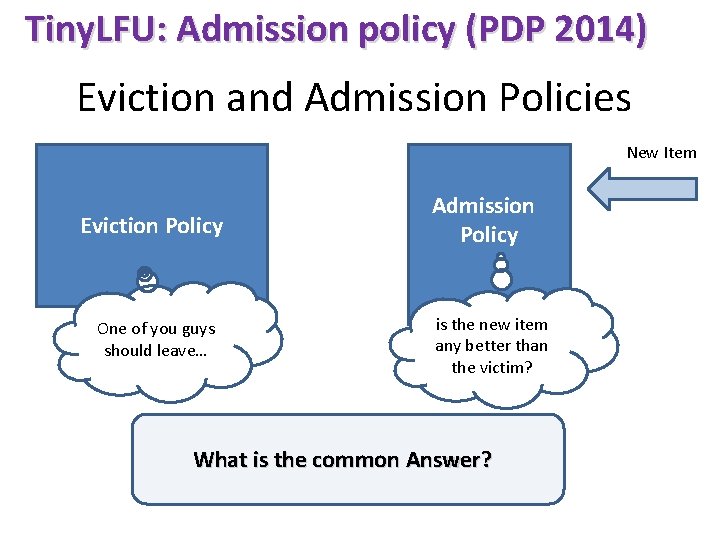
Tiny. LFU: Admission policy (PDP 2014) Eviction and Admission Policies Cache Victim Eviction Policy One of you guys should leave… New Item Admission Policy Winner is the new item any better than the victim? What is the common Answer?

Tiny. LFU: (PDP 2014) Use a sample of recent events to manage cache. (alternative implementation) Tiny. Table

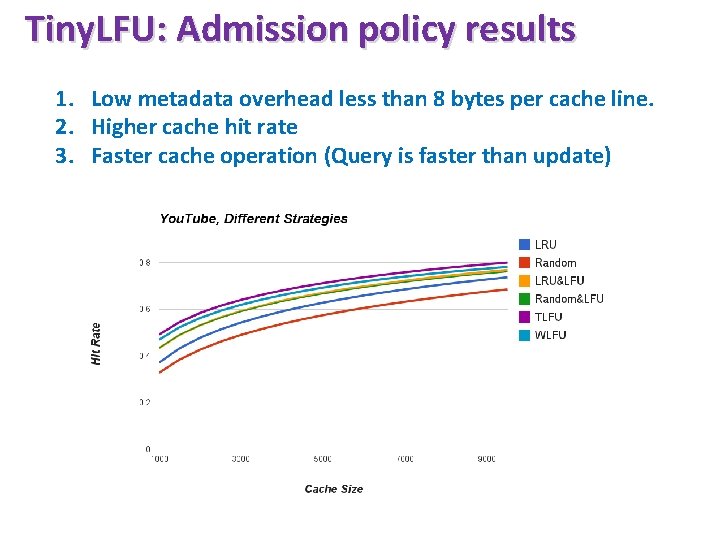
Tiny. LFU: Admission policy results 1. Low metadata overhead less than 8 bytes per cache line. 2. Higher cache hit rate 3. Faster cache operation (Query is faster than update)

Tiny. Table is soon to be released as an open source project. Tiny. LFU was released as the Shades open source project. I believe there are many other applications! Thank you for your Time! (and use my hash table – it is awesome)