Comp Sci 201 Data Representation Huffman Coding Owen

Comp. Sci 201 Data Representation & Huffman Coding Owen Astrachan Jeff Forbes November 29, 2017 11/29/17 Comp. Sci 201, Fall 2017, Data Rep 1

X is for … • XOR • (A || B) && !(A && B) • XML • Extensible Markup Language • Xerox PARC • GUIs, laser printers, OOP, ubicomp • Xavier • Winning 11/29/17 Compsci 201, Fall 2017, Data Rep 2

Getting Help on Piazza • Help us help you! • Where does your code hurt? • What have you tested on your own? How do you know your code is correct? • Issues • Referring to the writeup & previous questions • Common problems • Not a remote diagnostic service • Public vs. private questions 11/29/17 Compsci 201, Fall 2017, Data Rep 3

What’s left? • Huffman Coding • Data Representation • Huffman Coding • Compression • Decompression • Graphs • Upcoming • APT Quiz 3

Data and its Implications 11/29/17 Compsci 201, Fall 2017, Data Rep 5

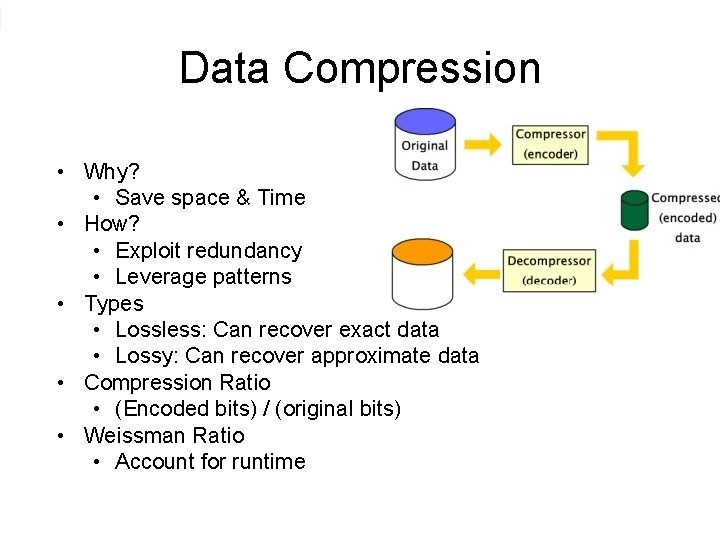
Data Compression • Why? • Save space & Time • How? • Exploit redundancy • Leverage patterns • Types • Lossless: Can recover exact data • Lossy: Can recover approximate data • Compression Ratio • (Encoded bits) / (original bits) • Weissman Ratio • Account for runtime

Compression! • From Silicon Valley • From Fall 2007: Huff that Code! • Jasdeep Garcha, Vyshak Chandra, Jonathan Wall, and Matt Mc. Kenna

Solving the problem • Steps to developing a usable algorithm. • Identify and model the problem. • Find an algorithm to solve it. • Fast enough? Fits in memory? • If not, figure out why. • Find a way to address the problem. • Iterate until satisfied. • The scientific method. • Mathematical analysis.

Data Representation • Ultimately everything is stored as either a 0 or 1 • Bit is binary digit a byte is a binary term (8 bits) • We should be thankful we can deal with Strings rather than sequences of 0's and 1's. • We should be thankful we can deal with an int rather than the 32 bits that comprise an int • Program using abstractions and high level concepts • Do we need to understand 32 -bit twos-complement storage to understand x =x+1? • Do we need to understand how arrays map to contiguous memory to use Array. Lists? • Top-down vs. bottom-up?

Primitive types • Some applications require attention to memory-use • Differences: one-million bytes, chars, and int • First requires a megabyte, last requires four megabytes • When do we care about these differences? • int values are stored as two's complement numbers with 32 bits, for 64 bits use the type long, a char is 16 bits • Java byte, int, long are signed values, char unsigned • Java signed byte: -128. . 127, # bits? • What if we only want 0 -255? (Huff, pixels, …) • Convert negative values or use char, trade-offs? • Java char unsigned: 0. . 65, 536 # bits? • Why is char unsigned?

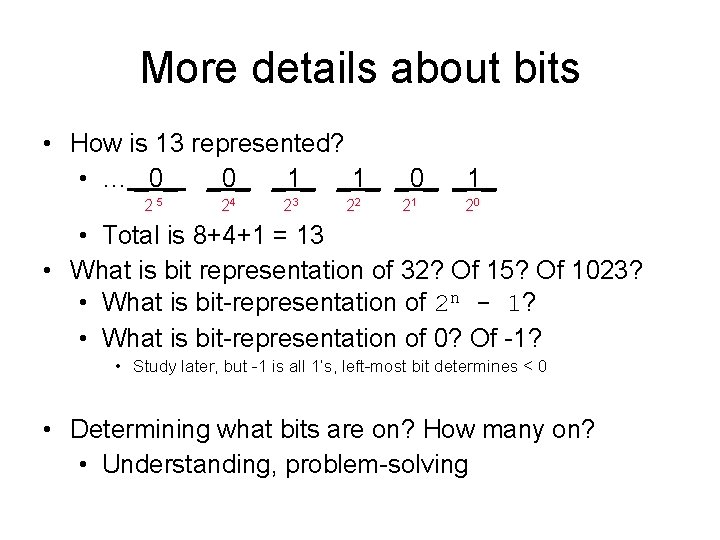
More details about bits • How is 13 represented? • … _0_ _1_ _0_ _1_ 2 5 24 23 22 21 20 • Total is 8+4+1 = 13 • What is bit representation of 32? Of 15? Of 1023? • What is bit-representation of 2 n - 1? • What is bit-representation of 0? Of -1? • Study later, but -1 is all 1’s, left-most bit determines < 0 • Determining what bits are on? How many on? • Understanding, problem-solving

Text Compression: Examples “abcde” in the different formats ASCII: 011000010110001001101100100… Fixed: 000001010011100 1 Encodings ASCII: 8 bits/character Unicode: 16 or 32 bits/character Symbol a ASCII 01100001 Fixed length 000 0 0 Var. length 000 b 01100010 001 11 c 01100011 010 01 d 01100100 011 001 e 01100101 100 10 0 a Variable: 000110100110 1 1 b 0 0 1 c d 0 0 e 1 0 0 0 a 1 1 d c 0 e 1 b

Huffman Coding • • D. A Huffman in early 1950’s Before compressing data, analyze the input stream Represent data using variable length codes Variable length codes though Prefix codes • Each letter is assigned an encoding • Encoding is for a given letter is produced by traversing the Huffman tree • Property: No encoding produced is the prefix of another • Letters appearing frequently have short encoding, while those that appear rarely have longer ones • Huffman coding is optimal per-character coding method

Building a Huffman tree • Begin with a forest of single-node trees (leaves) • Each node/tree/leaf is weighted with character count • Node stores two values: character and count • There are n nodes in forest, n is size of alphabet? • Repeat until there is only one node left: root of tree • Remove two minimally weighted trees from forest Greedy! • Create new tree with minimal trees as children, • New tree root's weight: sum of children (character ignored) • Does this process terminate? How do we get minimal trees? • Remove minimal trees, need to order based on what?

Creating a Huffman Tree/Trie? • Insert weighted values into priority queue • What are initial weights? Why? • Remove minimal nodes, weight by sums, re-insert • Total number of nodes? Priority. Queue<Huff. Node> forest = new Priority. Queue<>(); for (int i = 0; i < 256; i++) if (frequencies[i] > 0) // computed elsewhere forest. add(new Huff. Node(i, frequencies[i])); while (forest. size() > 1) { Huff. Node left = forest. remove(); Huff. Node right = forest. remove(); forest. add(new Huff. Node(-1, left. weight()+right. weight(), left, right)); } Huff. Node root = forest. remove();

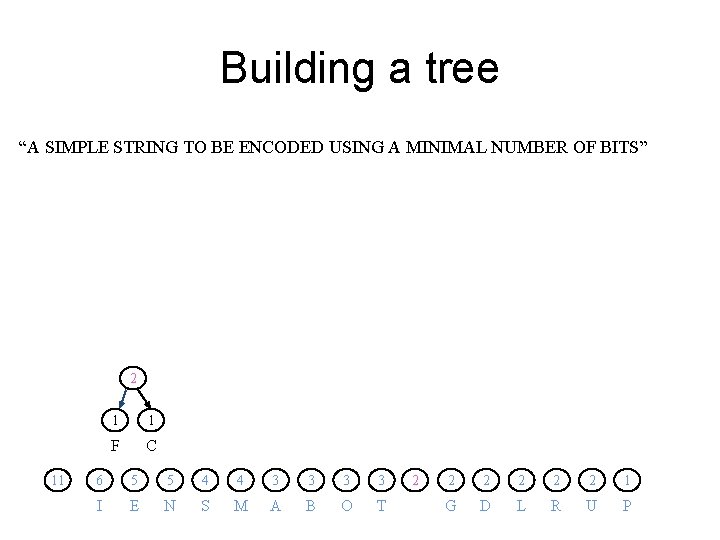
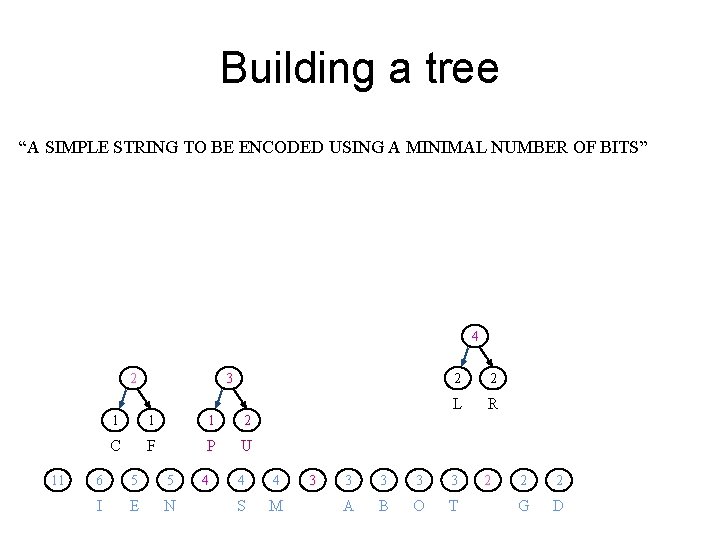
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 11 6 5 5 4 4 3 3 2 2 2 1 1 1 I E N S M A B O T G D L R U P F C

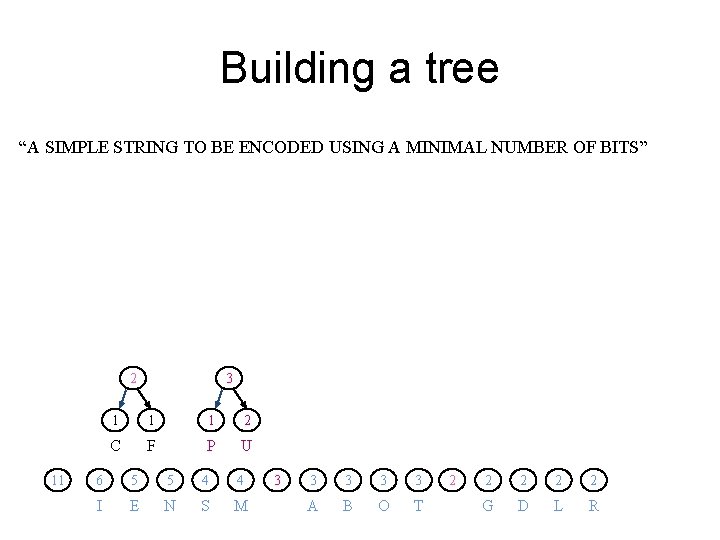
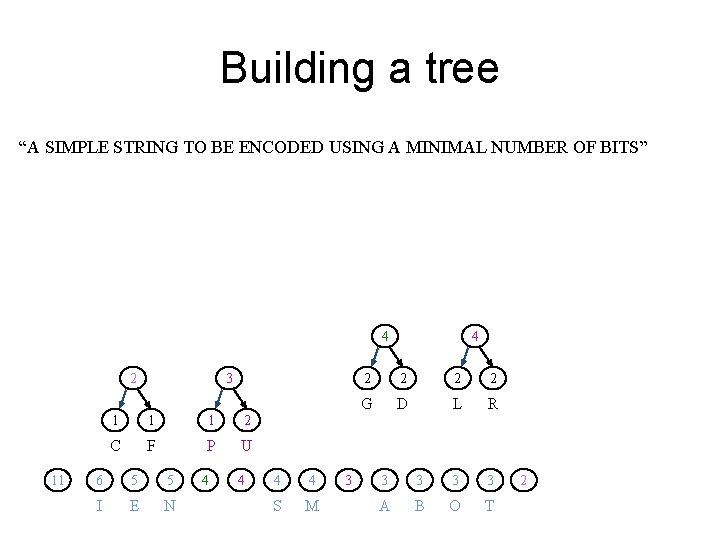
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 2 11 1 1 F C 6 5 5 4 4 3 3 I E N S M A B O T 2 2 2 1 G D L R U P

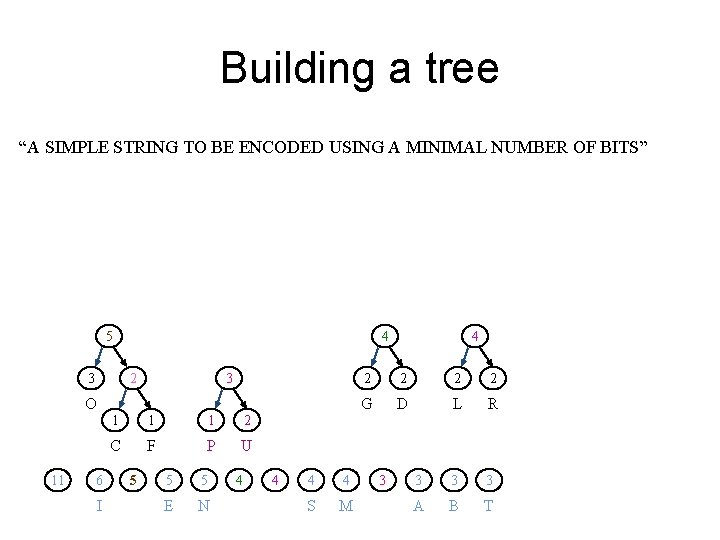
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 2 11 3 1 1 1 2 C F P U 6 5 5 4 4 I E N S M 3 3 3 A B O T 2 2 2 G D L R

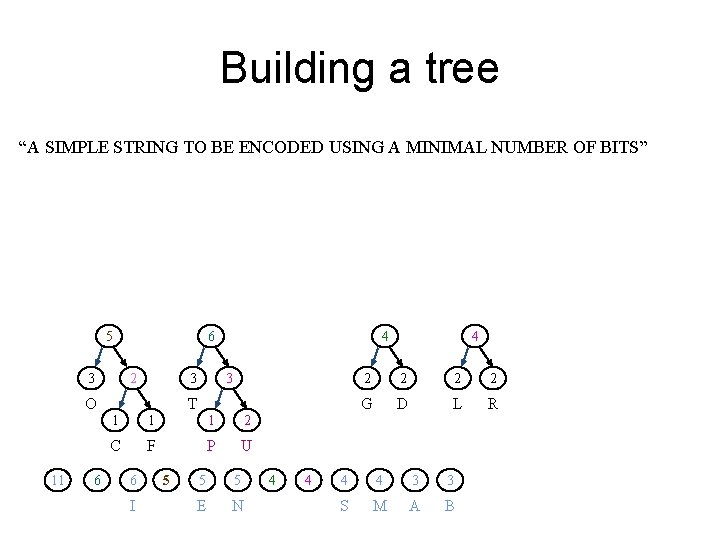
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 4 2 11 3 1 1 1 2 C F P U 6 5 5 I E N 4 4 4 S M 3 2 2 L R 2 3 3 A B O T 2 2 G D

Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 4 2 11 3 1 1 1 2 C F P U 6 5 5 I E N 4 4 S M 3 4 2 2 G D L R 3 3 A B O T 2

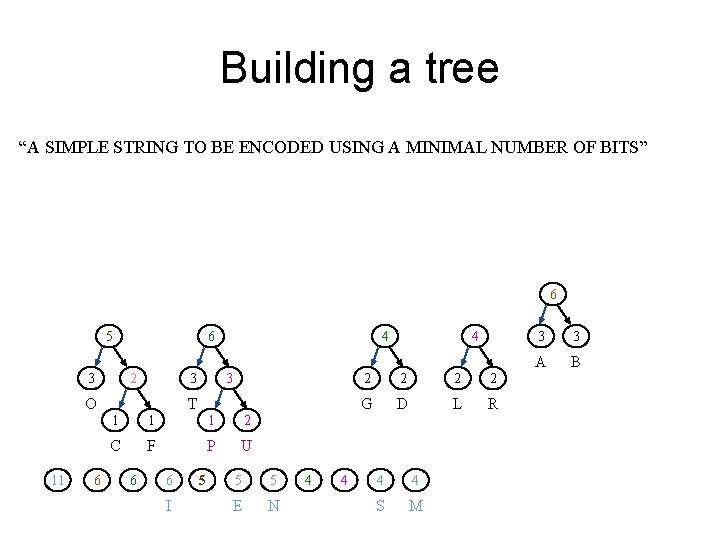
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 5 4 2 3 3 O 11 6 I 1 1 1 2 C F P U 5 5 5 E N 4 4 S M 4 2 2 G D L R 3 3 3 A B T 3

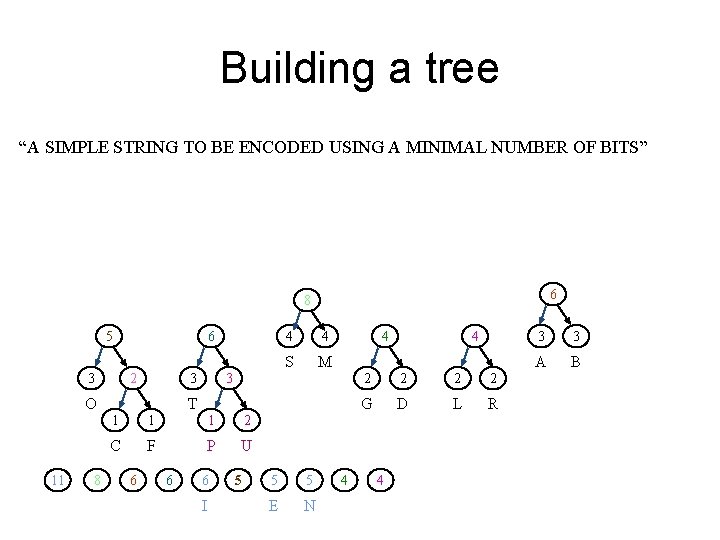
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 5 6 2 3 11 6 3 3 O 4 T 1 1 1 2 C F P U 6 I 5 5 5 E N 4 4 4 2 2 G D L R 4 4 3 3 S M A B

Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 6 5 6 2 3 11 6 3 3 O 4 T 1 1 1 2 C F P U 6 6 I 5 5 5 E N 4 4 4 2 2 G D L R 4 4 S M 3 3 A B

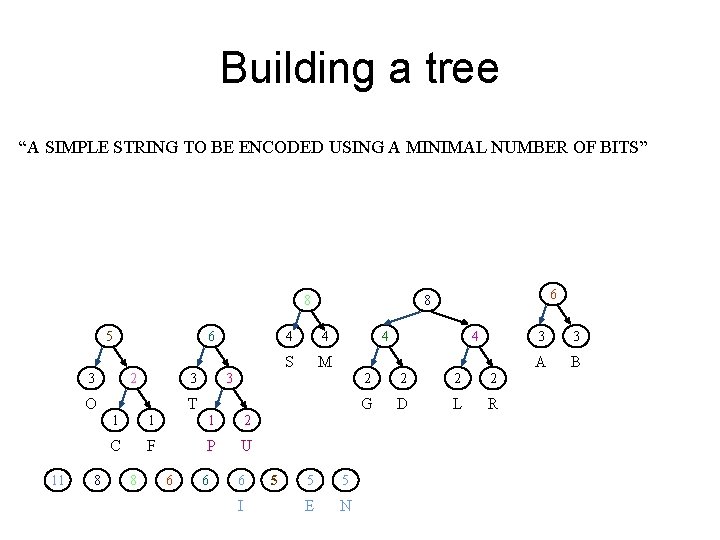
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 6 8 5 6 2 3 11 8 4 S M 4 3 3 O 4 T 1 1 1 2 C F P U 6 6 6 I 5 5 5 E N 4 4 2 2 G D L R 4 3 3 A B

Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 8 5 6 2 3 O 11 8 4 4 S M 4 3 3 T 1 1 1 2 C F P U 8 6 6 6 I 5 6 8 5 5 E N 4 2 2 G D L R 3 3 A B

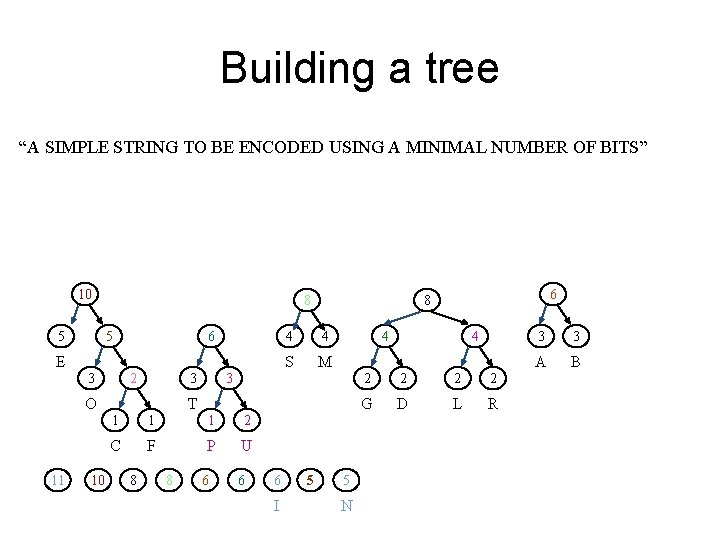
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 10 8 5 5 6 E 2 3 O 11 10 4 4 S M 4 3 3 T 1 1 1 2 C F P U 8 8 6 6 6 I 5 6 8 5 N 4 2 2 G D L R 3 3 A B

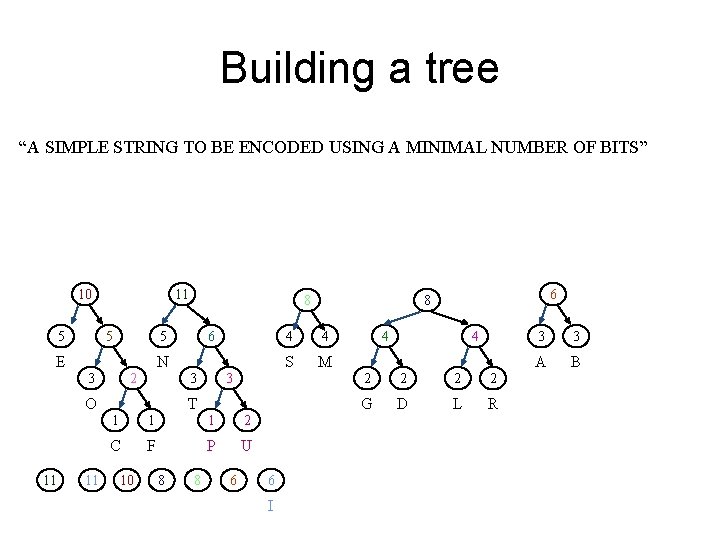
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 10 11 5 5 6 5 E N 2 3 11 3 3 O 11 8 T 1 1 1 2 C F P U 10 8 8 6 6 I 6 8 4 4 S M 4 4 2 2 G D L R 3 3 A B

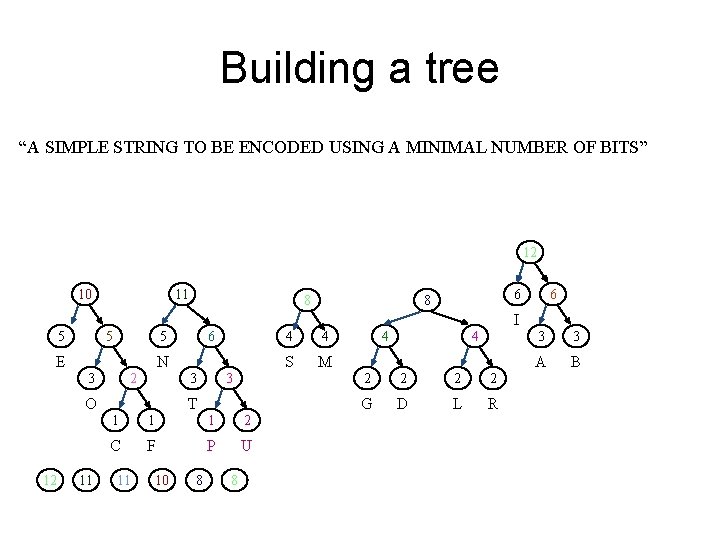
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 12 10 11 8 6 6 8 I 5 5 E N 2 3 11 3 3 O 12 6 5 T 1 1 1 2 C F P U 11 10 8 8 4 4 S M 4 4 2 2 G D L R 3 3 A B

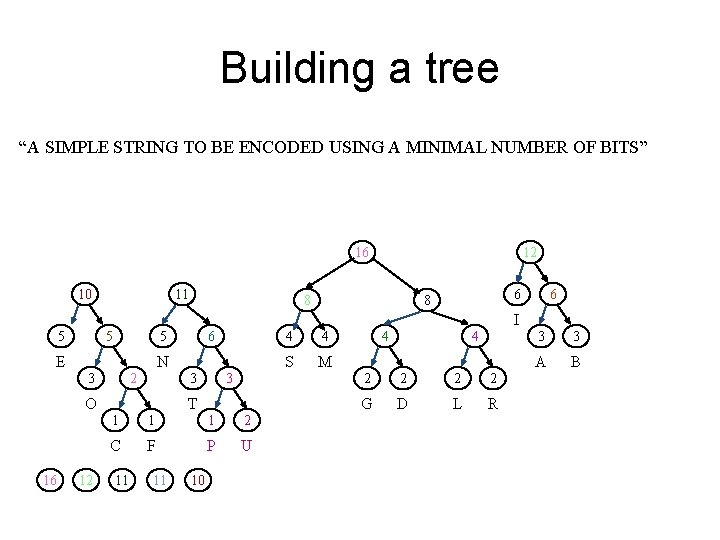
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 16 10 11 12 8 6 6 8 I 5 5 E N 2 3 12 3 3 O 16 6 5 T 1 1 1 2 C F P U 11 11 10 4 4 S M 4 4 2 2 G D L R 3 3 A B

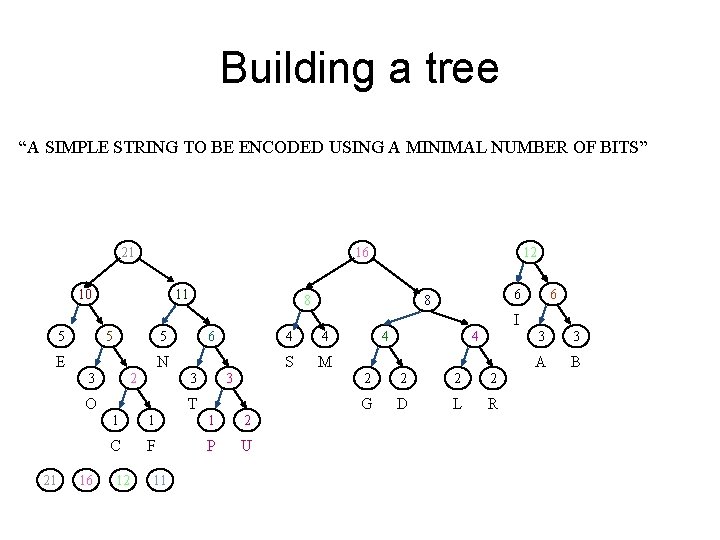
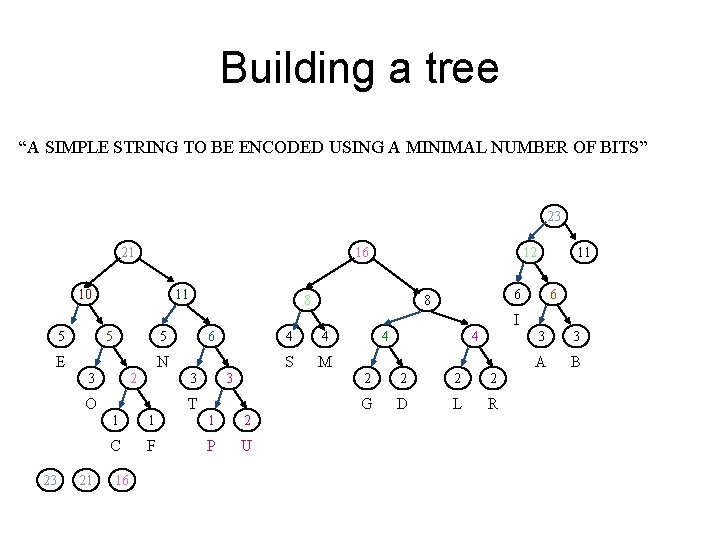
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 21 16 10 11 12 8 6 6 8 I 5 5 E N 2 3 16 3 3 O 21 6 5 T 1 1 1 2 C F P U 12 11 4 4 S M 4 4 2 2 G D L R 3 3 A B

Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 23 21 16 10 11 12 8 11 6 6 8 I 5 5 E N 2 3 21 3 3 O 23 6 5 T 1 1 1 2 C F P U 16 4 4 S M 4 4 2 2 G D L R 3 3 A B

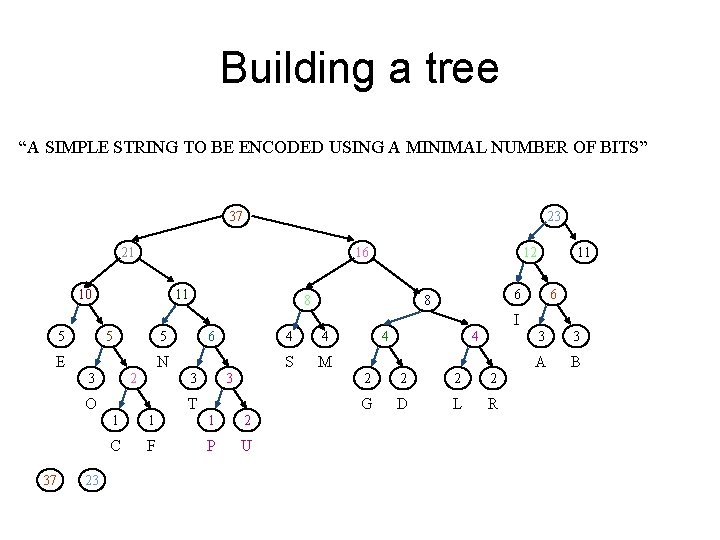
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 E N 2 3 23 3 3 O 37 6 5 T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R 3 3 A B

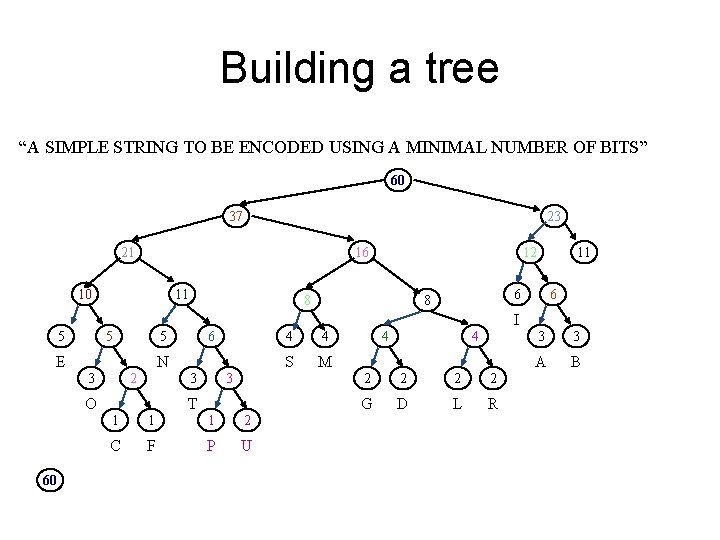
Building a tree “A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS” 60 37 23 21 16 10 11 12 8 11 6 8 6 I 5 5 5 E N 2 3 3 3 O 60 6 T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R 3 3 A B

Creating a Huffman Tree/Trie? • Insert weighted values into priority queue • What are initial weights? Why? • Remove minimal nodes, weight by sums, re-insert • Total number of nodes? Priority. Queue<Huff. Node> forest = new Priority. Queue<>(); for (int i = 0; i < 256; i++) if (frequencies[i] > 0) // computed elsewhere forest. add(new Huff. Node(i, frequencies[i])); while (forest. size() > 1) { Huff. Node left = forest. remove(); Huff. Node right = forest. remove(); forest. add(new Huff. Node(-1, left. weight()+right. weight(), left, right)); } Huff. Node root = forest. remove();

What’s a Huff. Node • Similar to: • Encodes String via links like a Trie • Two children like a Tree. Node public class Huff. Node implements Comparable<Huff. Node> { // Data private int my. Value, my. Weight; private Huff. Node my. Left, my. Right; // Constructors public Huff. Node(int value, int weight) public Huff. Node(int value, int weight, Huff. Node left, Huff. Node right) } 11/17/17 Compsci 201, Fall 2017, Tries+Greedy 35

Encoding • Given a file with: • n characters • an alphabet of k distinct characters, • r is the compression rate (bits/character) 1. Count occurrence of all occurring characters O( 2. Build priority queue n ) O( k lg k ) O( k ) 5. Write Huffman tree and coded data to file O( n ) 3. Build Huffman tree 4. Create Table of encodings from tree http: //bit. ly/201 -f 17 -1129 -1

Properties of Huffman coding • Want to minimize weighted path length L(T)of tree T • • wi is the weight or count of each encoding i • di is the leaf corresponding to encoding i • How do we calculate character (encoding) frequencies? • Huffman coding creates pretty full bushy trees? • When would it produce a “bad” tree? • How do we produce coded compressed data from input efficiently?

Writing code out to file • How do we go from characters to encodings? • Build Huffman tree • Root-to-leaf path generates encoding • Recall Leaf. Trails APT • Need way of writing bits out to file • Platform dependent? • Complicated to write bits and read in same ordering • See Bit. Input. Stream and Bit. Output. Stream classes • How do we know bits come from compressed file? • Store a magic number

Creating compressed file • Once we have new encodings, read every character • Write encoding, not the character, to compressed file • Why does this save bits? • What other information needed in compressed file? • How do we uncompress? • How do we know foo. hf represents compressed file? • Is suffix sufficient? Alternatives? • Why is Huffman coding a two-pass method? • Alternatives?

Uncompression with Huffman • We need the trie to uncompress • 00010011001101111 • As we read a bit, what do we do? • Go left on 0, go right on 1 • When do we stop? What to do? • How do we get the trie? • How did we get it originally? Store 256 int/counts • How do we read counts? • How do we store a trie? Traversal order? • Reading a trie? Leaf indicator? Node values? http: //bit. ly/201 -f 17 -1129 -2

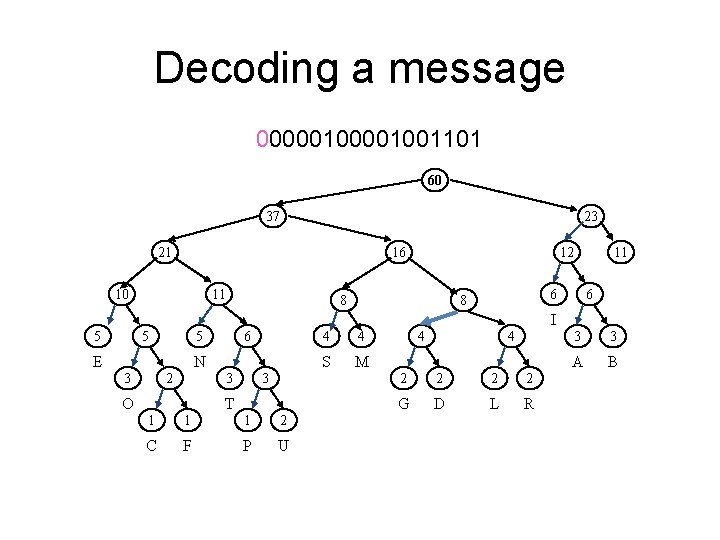
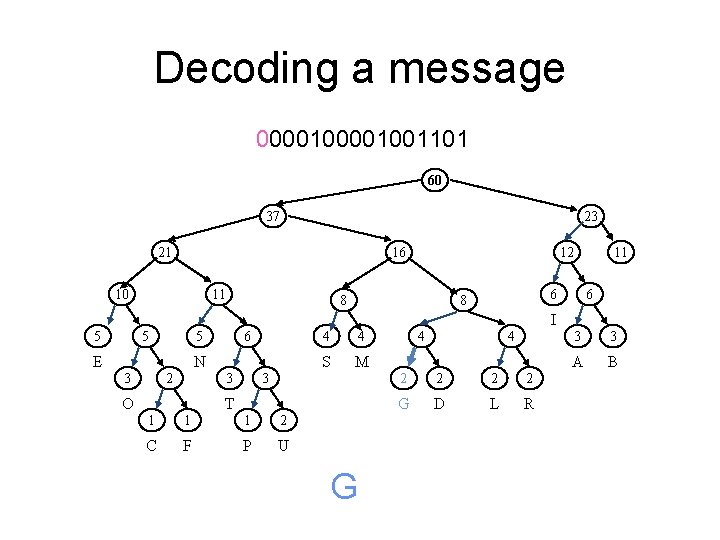
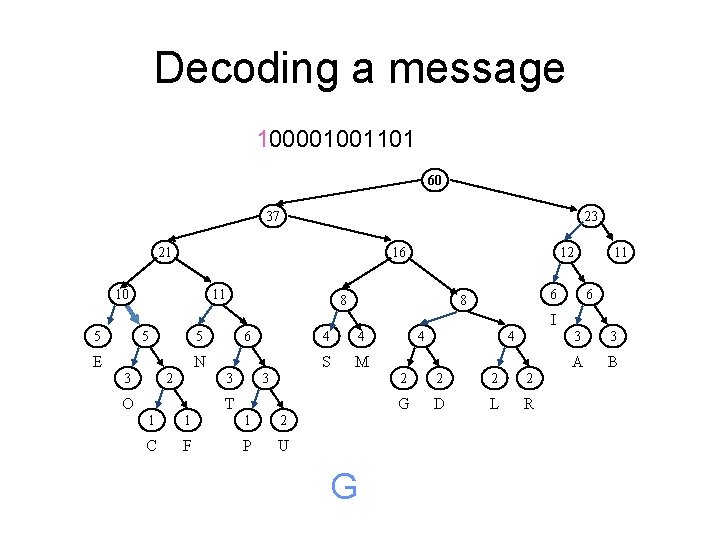
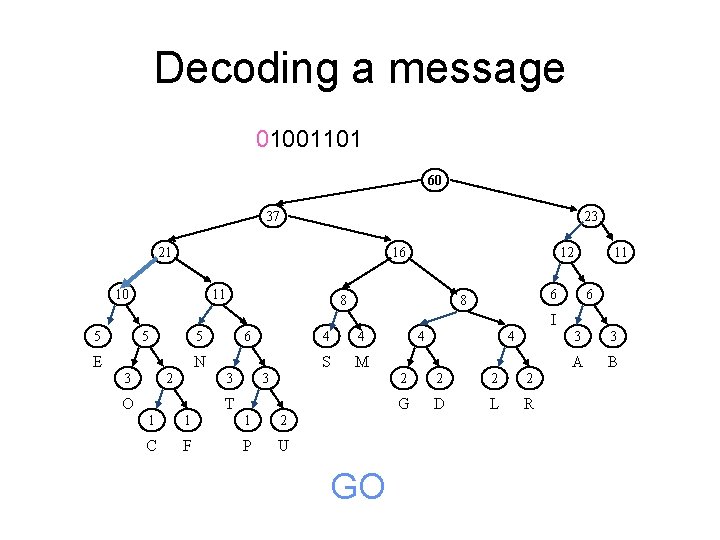
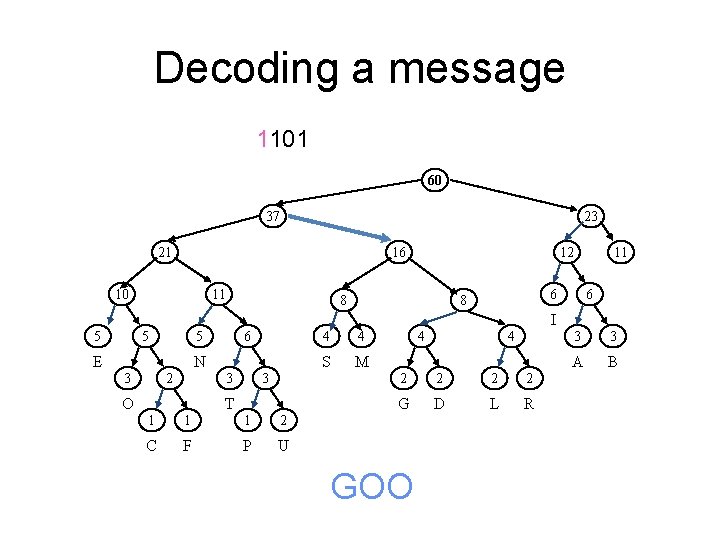
Decoding a message 000001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R 3 3 A B

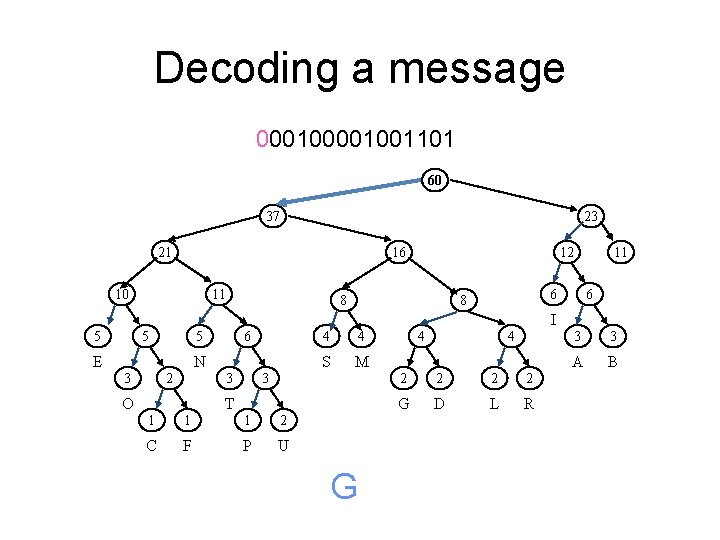
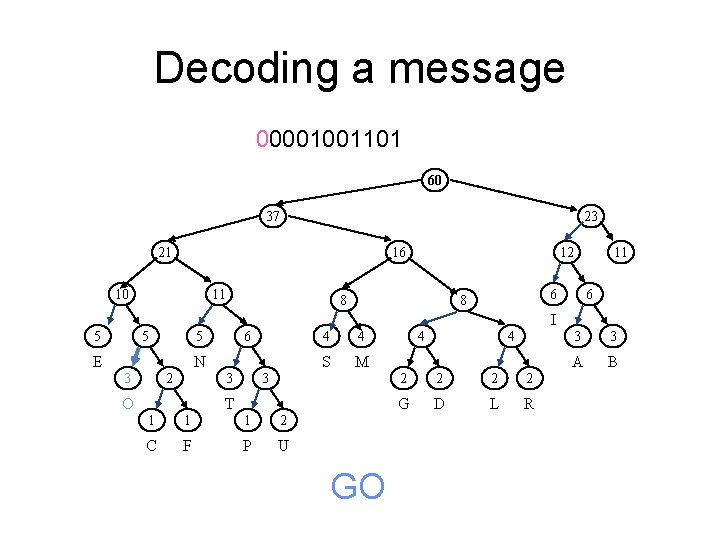
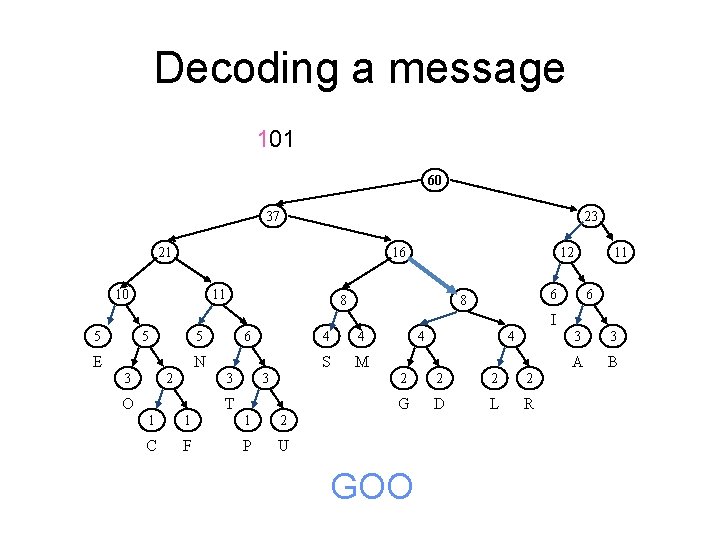
Decoding a message 00001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U G 4 4 2 2 G D L R 3 3 A B

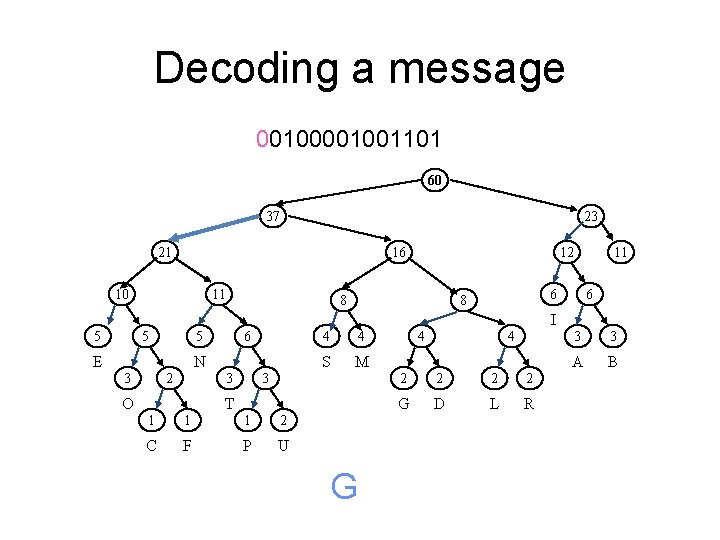
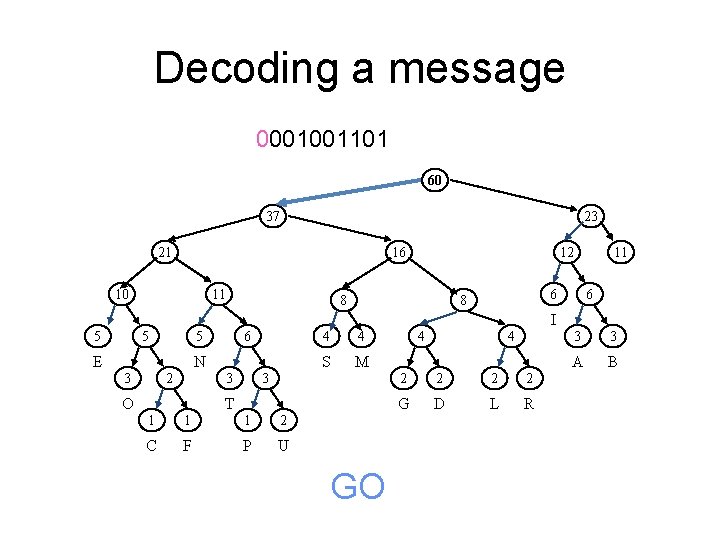
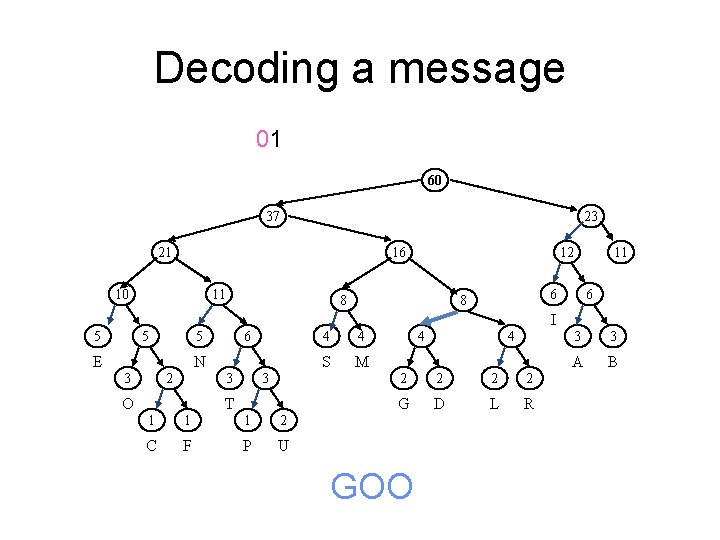
Decoding a message 0001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U G 4 4 2 2 G D L R 3 3 A B

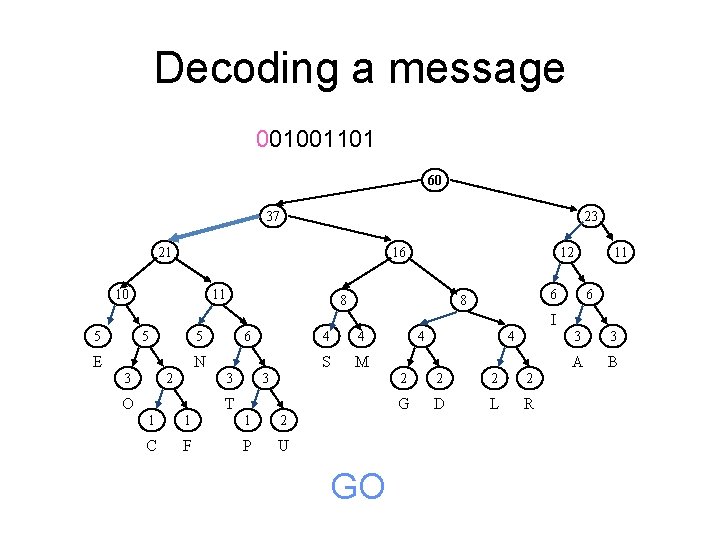
Decoding a message 001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U G 4 4 2 2 G D L R 3 3 A B

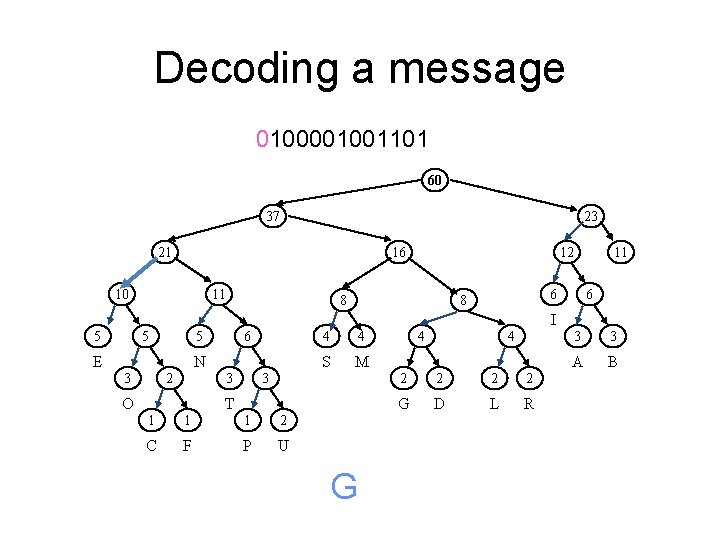
Decoding a message 0100001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U G 4 4 2 2 G D L R 3 3 A B

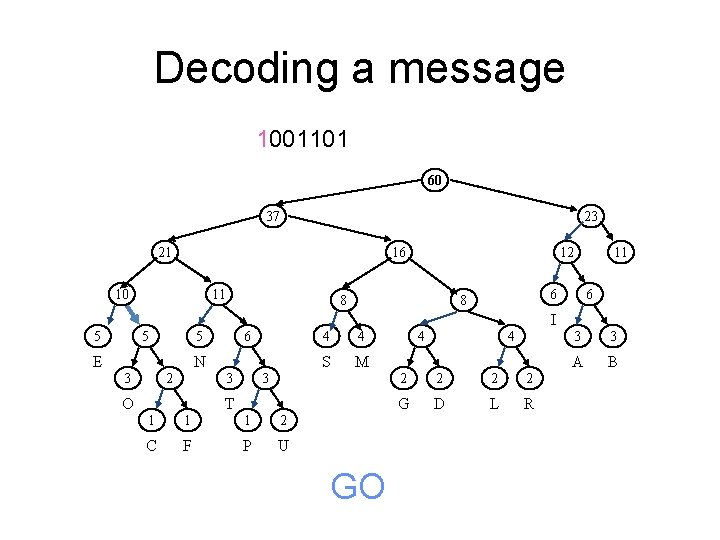
Decoding a message 100001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U G 4 4 2 2 G D L R 3 3 A B

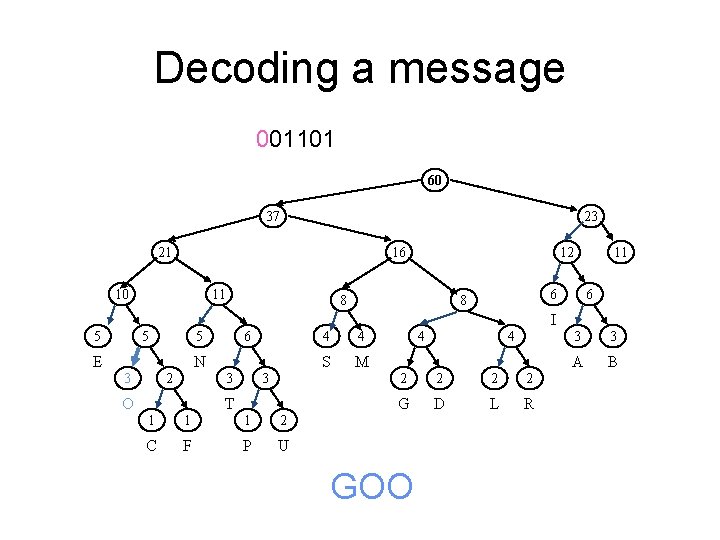
Decoding a message 00001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U GO 4 4 2 2 G D L R 3 3 A B

Decoding a message 0001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U GO 4 4 2 2 G D L R 3 3 A B

Decoding a message 001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U GO 4 4 2 2 G D L R 3 3 A B

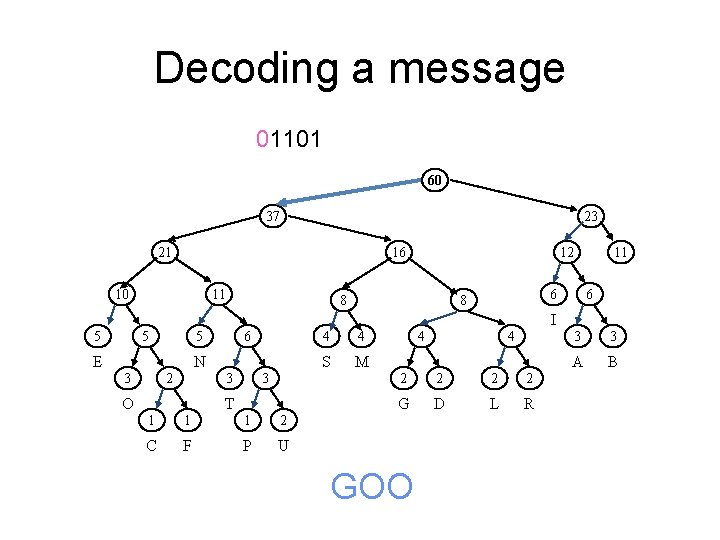
Decoding a message 01001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U GO 4 4 2 2 G D L R 3 3 A B

Decoding a message 1001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 4 S M 3 3 O 4 T 1 1 1 2 C F P U GO 4 4 2 2 G D L R 3 3 A B

Decoding a message 001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOO 3 3 A B

Decoding a message 01101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOO 3 3 A B

Decoding a message 1101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOO 3 3 A B

Decoding a message 101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOO 3 3 A B

Decoding a message 01 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOO 3 3 A B

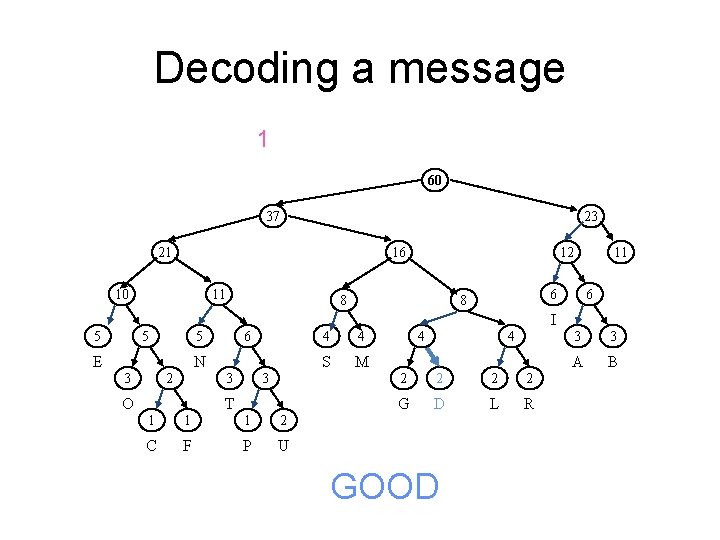
Decoding a message 1 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOOD 3 3 A B

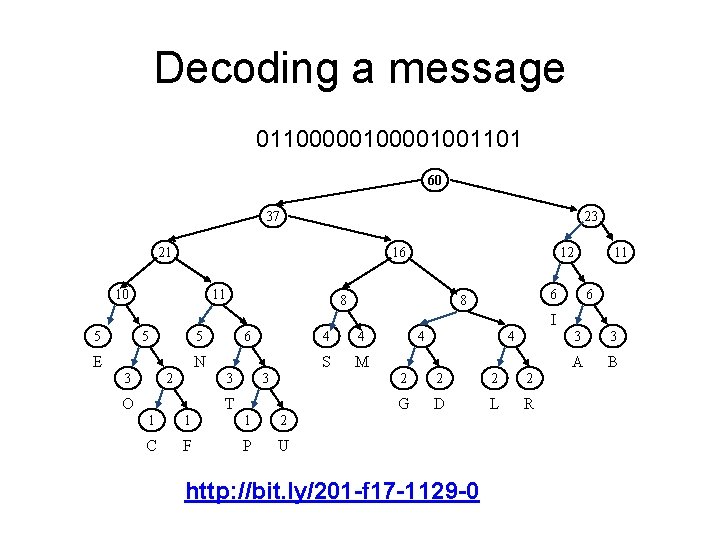
Decoding a message 011000001001101 60 37 23 21 16 10 11 12 8 11 6 6 8 I 5 5 6 5 E N 2 3 3 3 O T 1 1 1 2 C F P U 4 4 S M 4 4 2 2 G D L R GOOD http: //bit. ly/201 -f 17 -1129 -0 3 3 A B

Decoding • Given a file with: • n characters • an alphabet of k distinct characters, • r is the compression rate (bits/character) 1. Read in tree data 2. Decode bit string with tree O( O( k nr ) )

Data Compression Year Scheme Bit/Char 1967 ASCII 7. 00 1950 Huffman 4. 70 1977 Lempel-Ziv (LZ 77) 3. 94 1984 Lempel-Ziv-Welch (LZW) – Unix compress 3. 32 1987 (LZH) used by zip and unzip 3. 30 1987 Move-to-front 3. 24 1987 gzip 2. 71 1995 Burrows-Wheeler 2. 29 1997 BOA (statistical data compression) 1. 99 • Why is data compression important? • How well can you compress files losslessly? • Is there a limit? • How to compare? • How do you measure how much information?