Comp Sci 105 SS 2006 Principles of Computer

Comp. Sci 105 SS 2006 Principles of Computer Science Lecture 21: Binary Search Tree 1

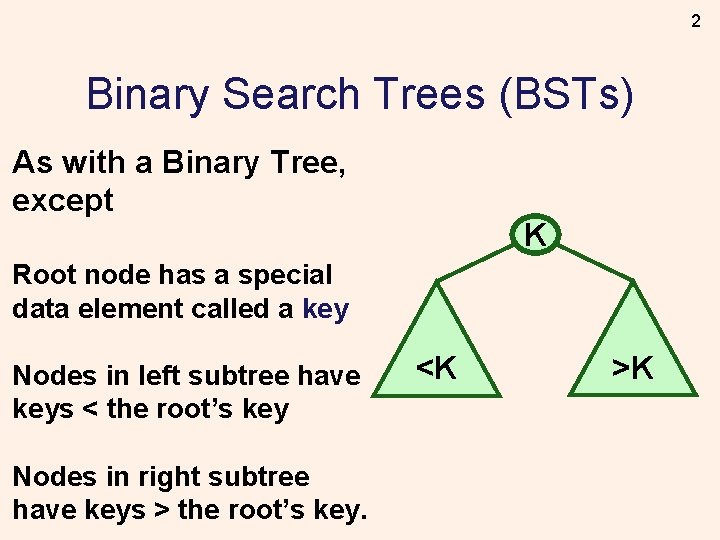
2 Binary Search Trees (BSTs) As with a Binary Tree, except K Root node has a special data element called a key Nodes in left subtree have keys < the root’s key Nodes in right subtree have keys > the root’s key. <K >K

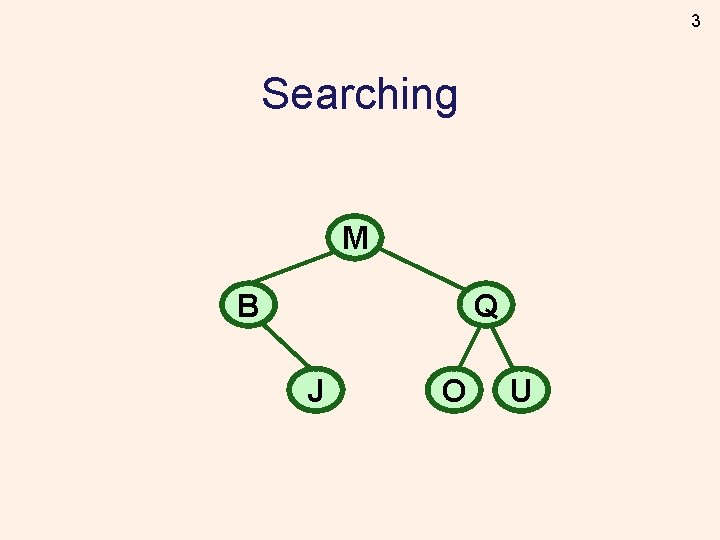
3 Searching M B Q J O U

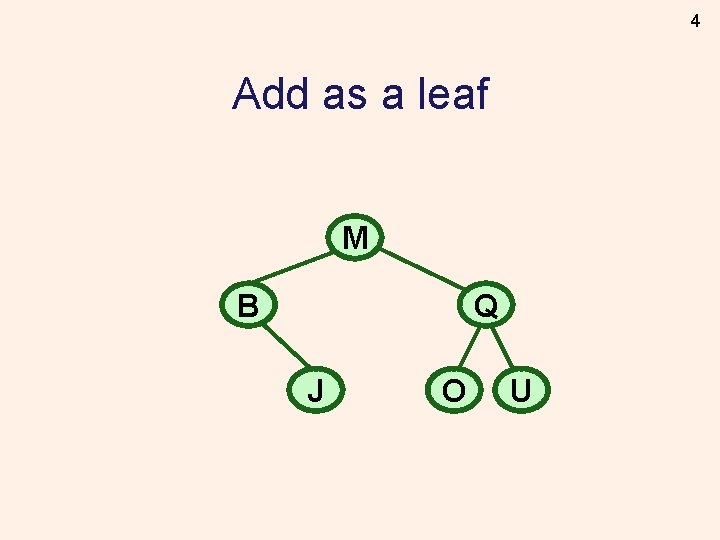
4 Add as a leaf M B Q J O U

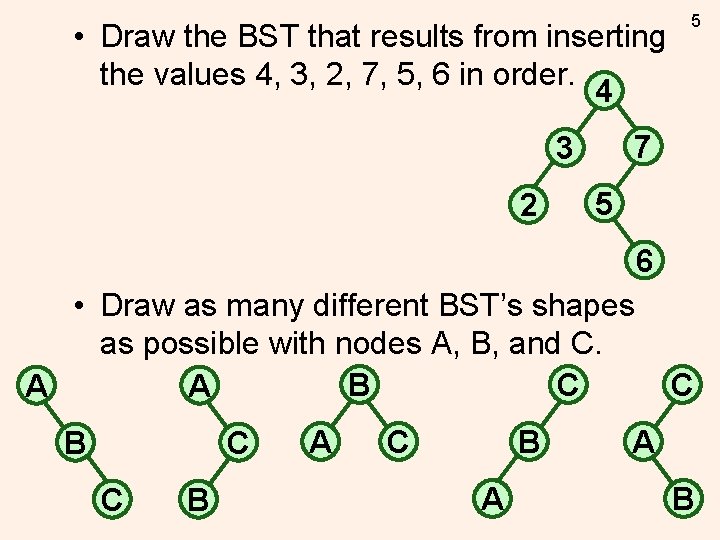
• Draw the BST that results from inserting the values 4, 3, 2, 7, 5, 6 in order. 4 7 3 2 5 5 6 • Draw as many different BST’s shapes as possible with nodes A, B, and C. B C A A B C C B A C A B

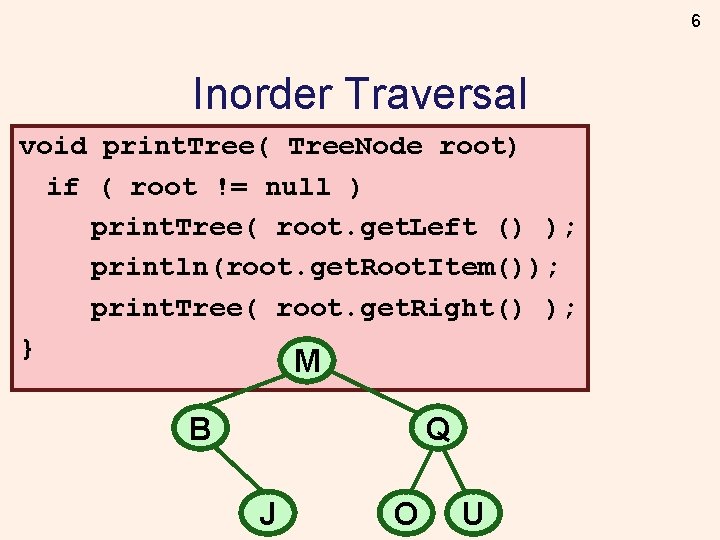
6 Inorder Traversal void print. Tree( Tree. Node root) if ( root != null ) print. Tree( root. get. Left () ); println(root. get. Root. Item()); print. Tree( root. get. Right() ); } M B Q J O U

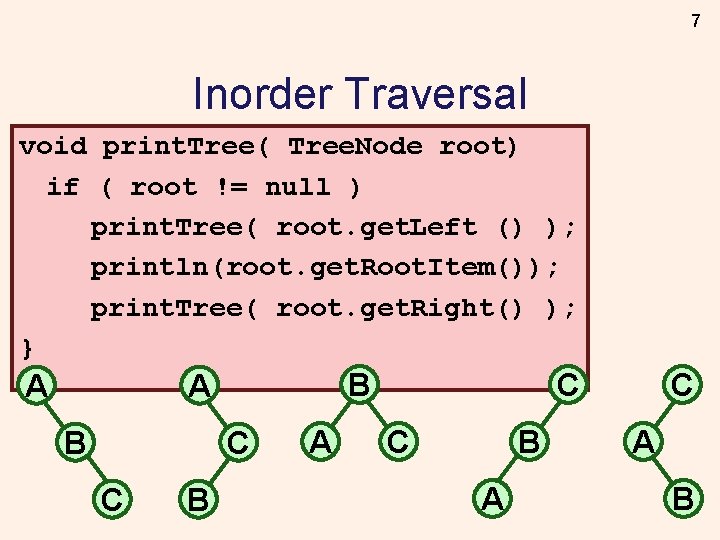
7 Inorder Traversal void print. Tree( Tree. Node root) if ( root != null ) print. Tree( root. get. Left () ); println(root. get. Root. Item()); print. Tree( root. get. Right() ); } A B C C B A C A B

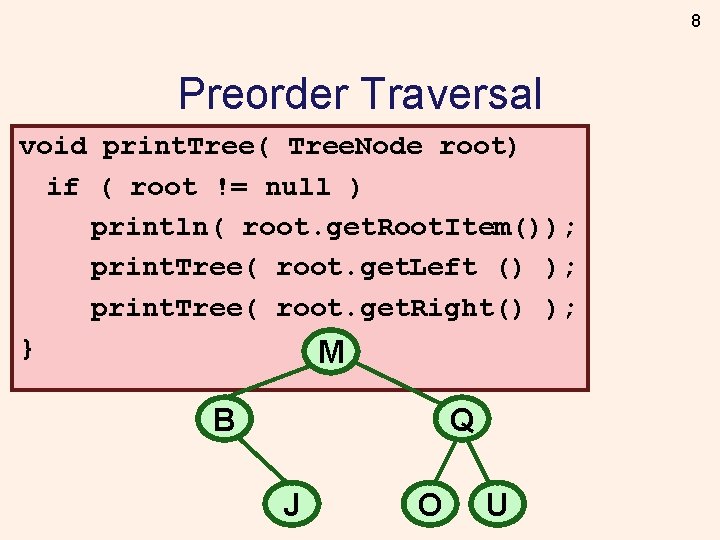
8 Preorder Traversal void print. Tree( Tree. Node root) if ( root != null ) println( root. get. Root. Item()); print. Tree( root. get. Left () ); print. Tree( root. get. Right() ); } M B Q J O U

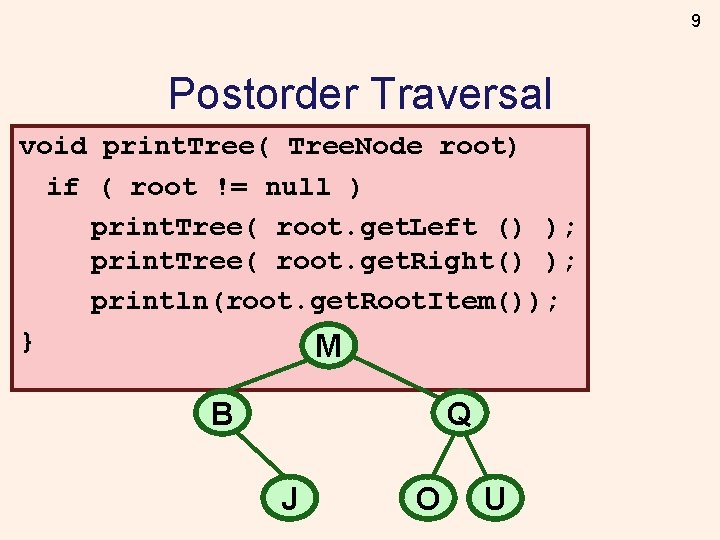
9 Postorder Traversal void print. Tree( Tree. Node root) if ( root != null ) print. Tree( root. get. Left () ); print. Tree( root. get. Right() ); println(root. get. Root. Item()); } M B Q J O U

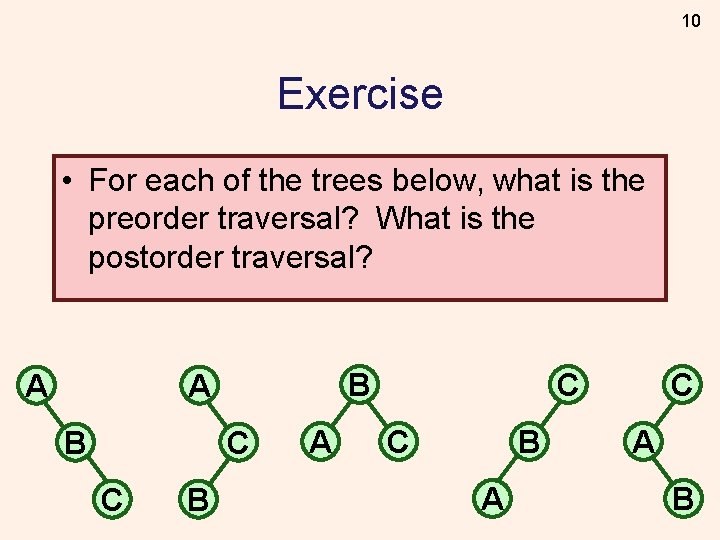
10 Exercise • For each of the trees below, what is the preorder traversal? What is the postorder traversal? A B C C B A C A B

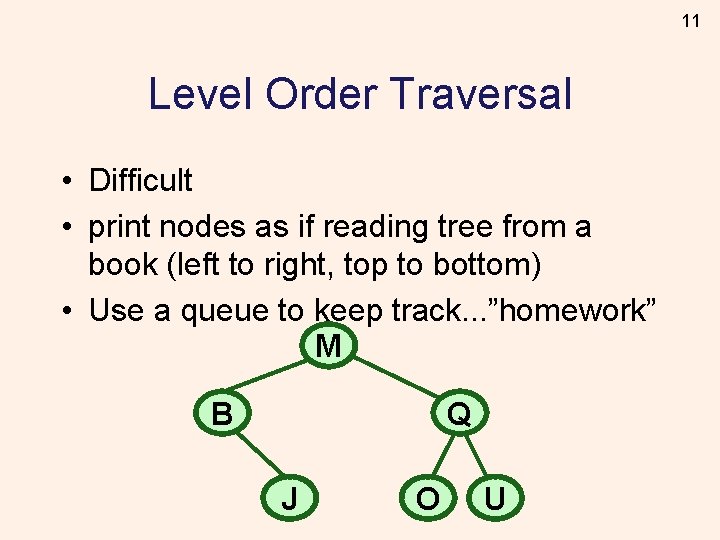
11 Level Order Traversal • Difficult • print nodes as if reading tree from a book (left to right, top to bottom) • Use a queue to keep track. . . ”homework” M B Q J O U

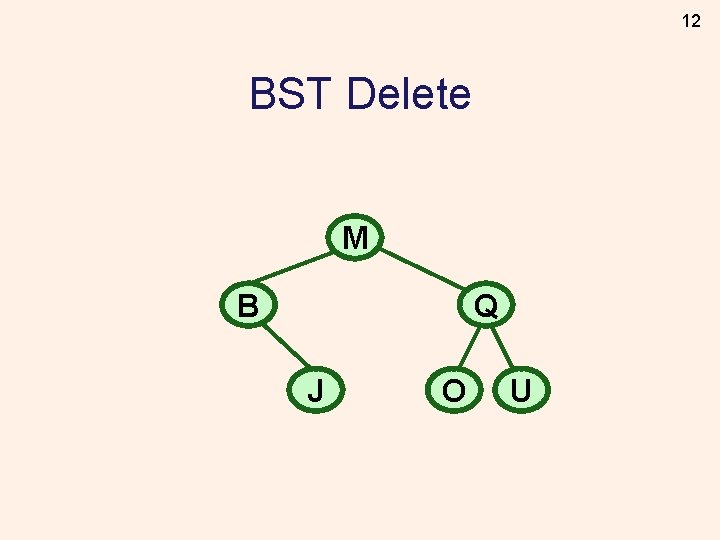
12 BST Delete M B Q J O U

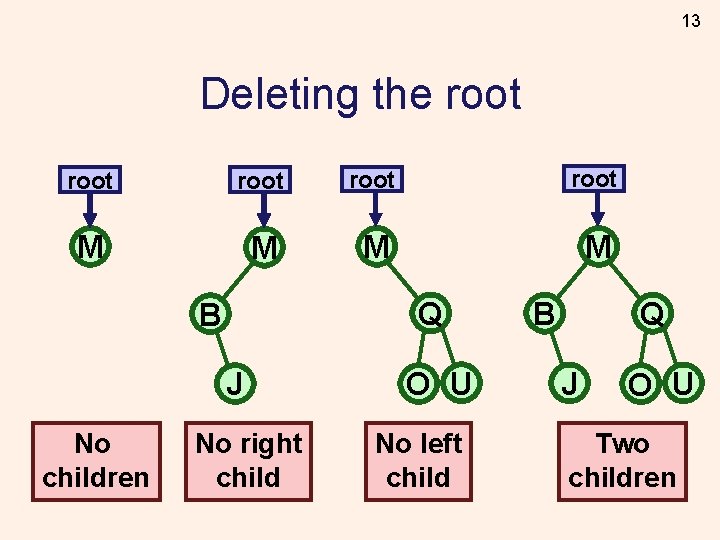
13 Deleting the root root M M Q B J No children No right child O U No left child B Q J O U Two children

14 Exercise • Draw the BST that results from inserting the values D, C, G, B, E, F in order. Now draw the result of deleting the root.

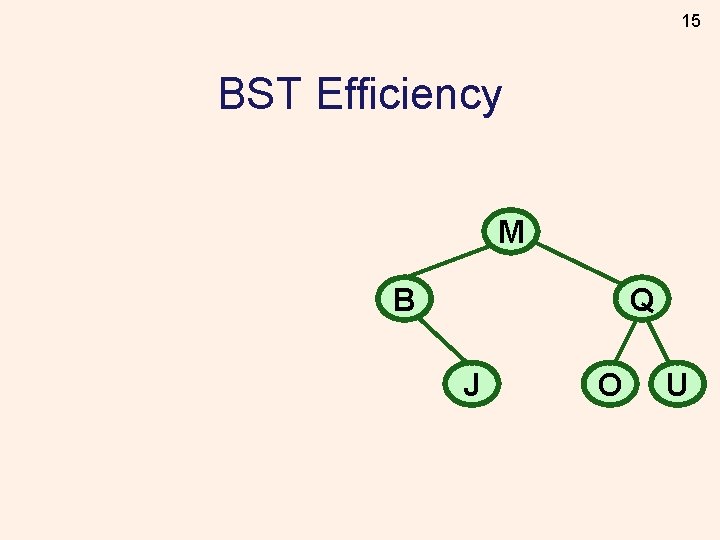
15 BST Efficiency M B Q J O U

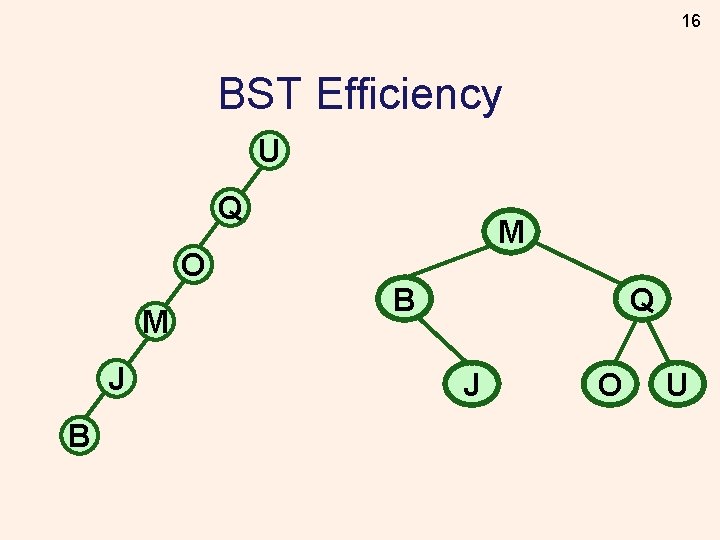
16 BST Efficiency U Q O M J B M B Q J O U

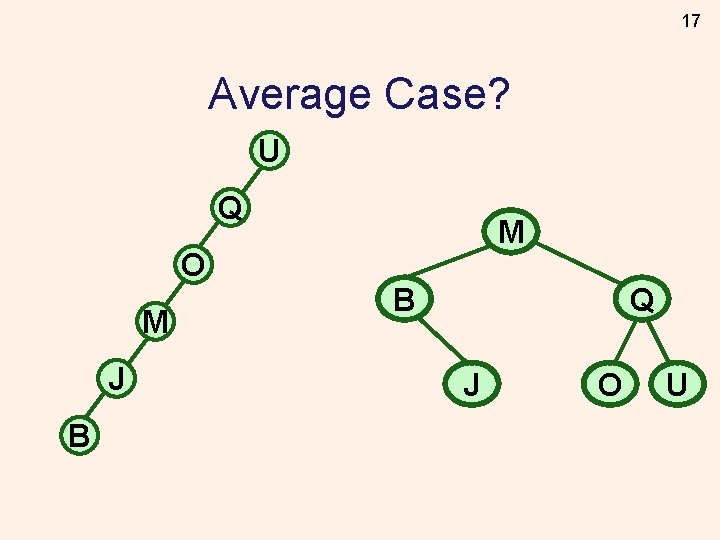
17 Average Case? U Q O M J B M B Q J O U

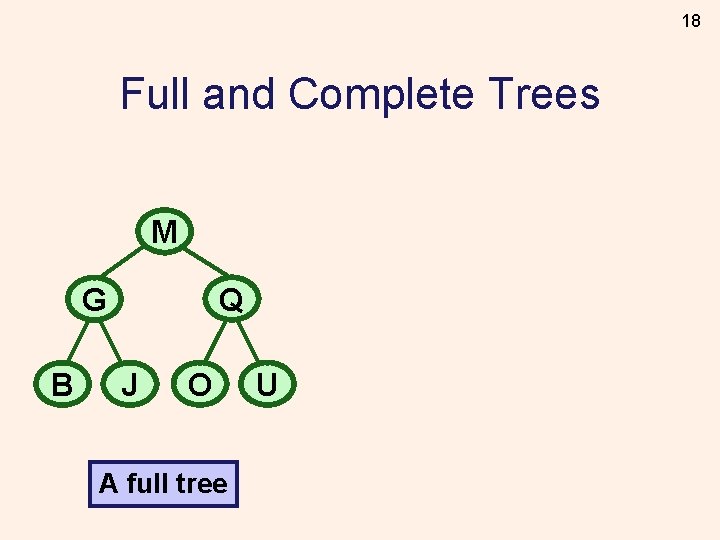
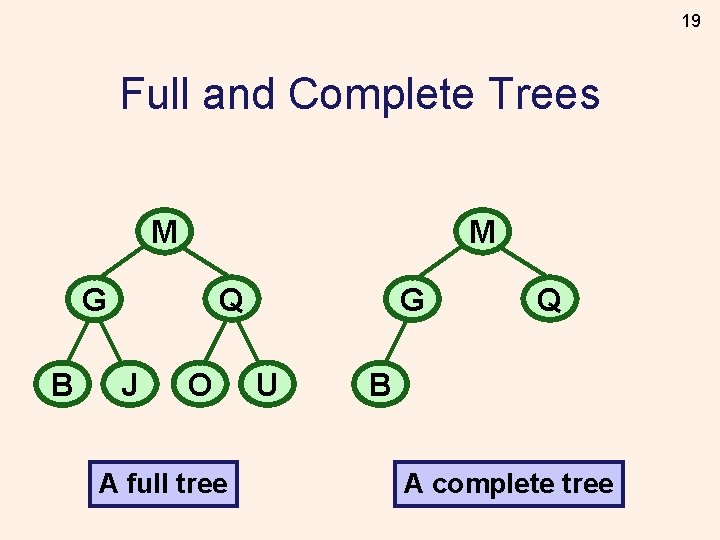
18 Full and Complete Trees M Q G B J O A full tree U

19 Full and Complete Trees M M Q G B J O A full tree G U Q B A complete tree

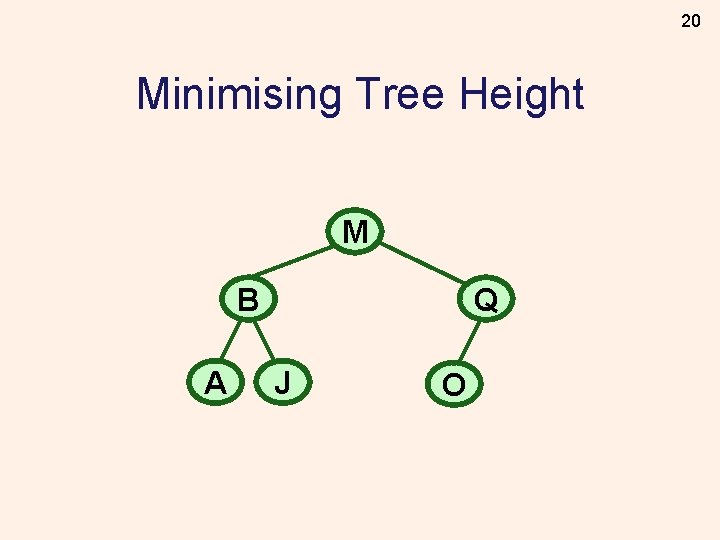
20 Minimising Tree Height M B A Q J O

21 Priority Queue Operations void create () boolean is. Empty() void insert( item) item delete() To do: 1. Study for 105 Exam 2. Play 3. Eat 4. 4. Sleep Textbook, p. 518

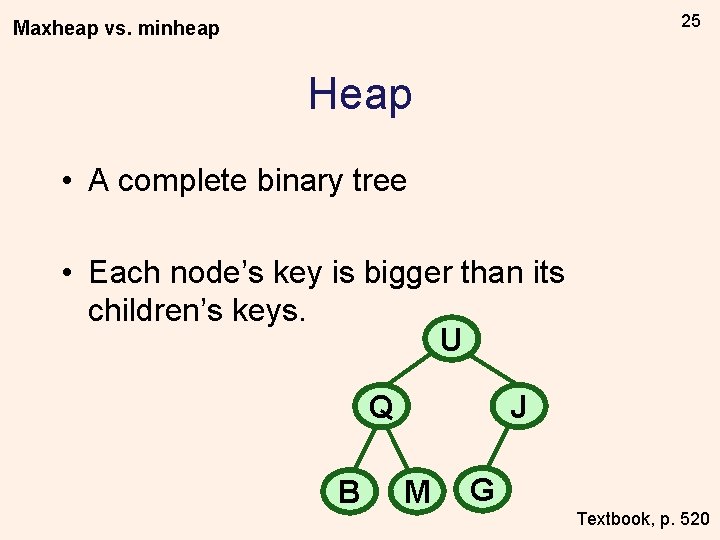
22 Heap Like a binary search tree, but • Always keep it a complete tree • Don’t completely sort data … just make sure that each node’s key is bigger than its children’s keys. Textbook, p. 520

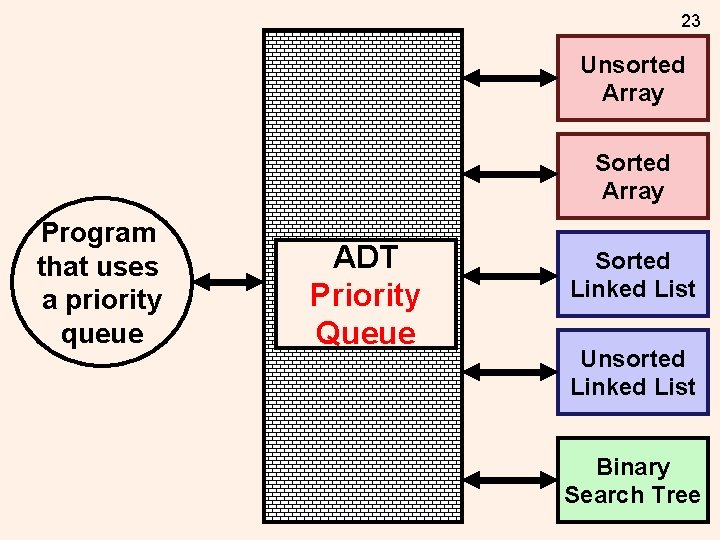
23 Unsorted Array Sorted Array Program that uses a priority queue ADT Table Priority Queue Sorted Linked List Unsorted Linked List Binary Search Tree

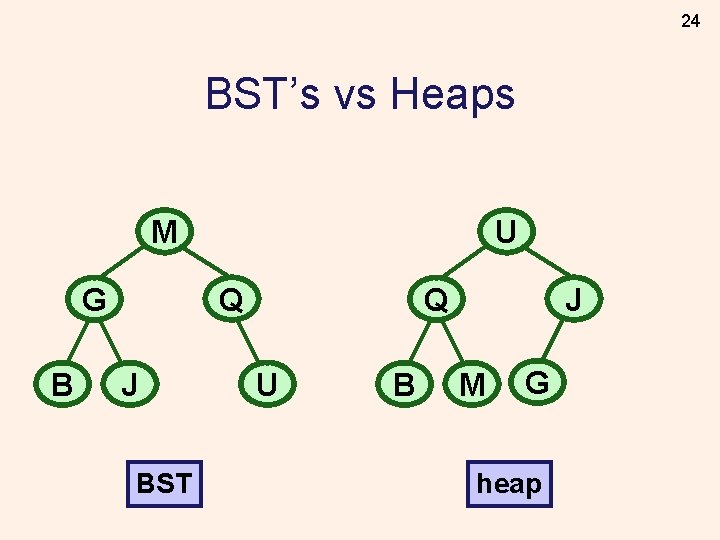
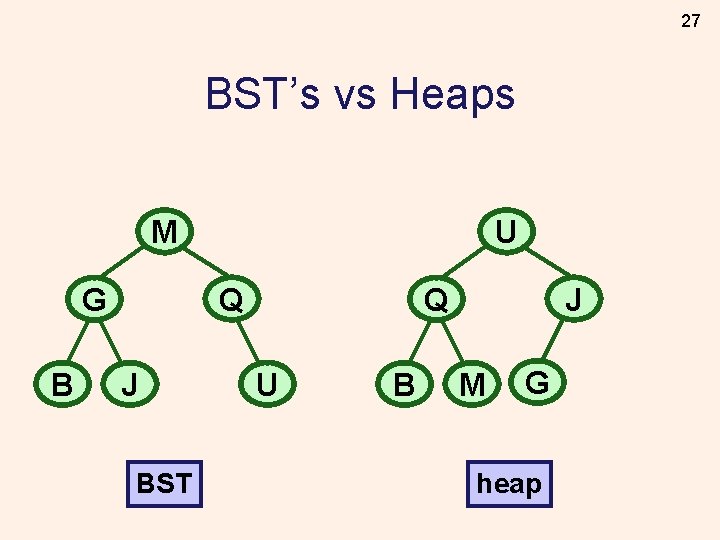
24 BST’s vs Heaps M Q G B U J BST J Q U B M G heap

25 Maxheap vs. minheap Heap • A complete binary tree • Each node’s key is bigger than its children’s keys. U J Q B M G Textbook, p. 520

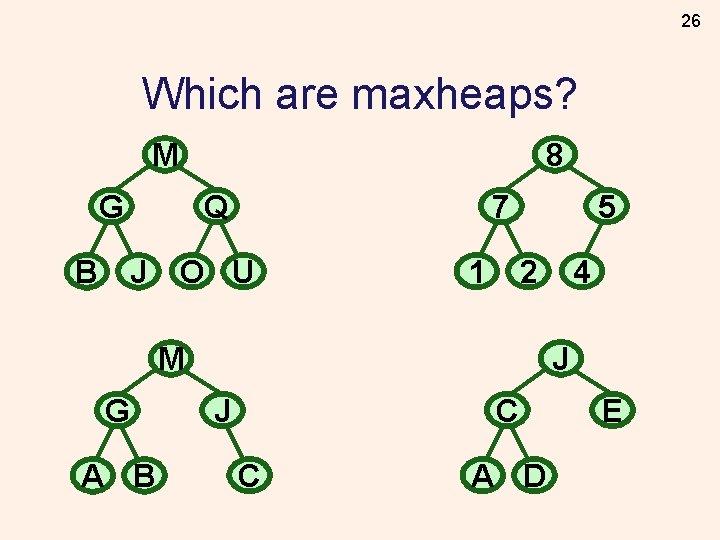
26 Which are maxheaps? 8 M 5 7 G Q B J O U 1 J M G A B 4 2 C J C A D E

27 BST’s vs Heaps M Q G B U J BST J Q U B M G heap