COMP 175 COMPUTER GRAPHICS Lecture 10 Illumination COMP

COMP 175 | COMPUTER GRAPHICS Lecture 10: Illumination COMP 175: Computer Graphics March 25, 2020 Remco Chang 10 – Lighting and Illumination 1/70

COMP 175 | COMPUTER GRAPHICS Summary: � Pseudocode for a non-recursive ray tracer: P = eye. Point for each pixel d = Compute Ray in World Coordinate for each object intersect P+td with object, record t and object Select object with smallest non-negative t value Find intersection point in Object Coordinate Compute normal of the point in Object Coordinate Transform normal to World Coordinate Solve lighting equation in World Coordinate Set Pixel Color Remco Chang 10 – Lighting and Illumination 2/70

COMP 175 | COMPUTER GRAPHICS Note about Ray � An important point about transforming Ray from World space to Object space: � Normalize the Ray after it’s created in World space. � However, do NOT normalize Ray after the transform into Object Space!! � Reason: � � If you normalize, then the value t you find will be in the object space. When there are many objects, it’s hard to figure out how to compare all the different t values across different object spaces If you do not normalize, then the value t will apply in the world space. That means that you can compare the t values derived from the different objects in the same coordinate. � Think about it a little bit… This is the only time in this class where you should not normalize a vector. Remco Chang 10 – Lighting and Illumination 3/70

COMP 175 | COMPUTER GRAPHICS Overview of Lighting � Different types of lighting (diffuse, specular, ambient, etc. ) � In almost all cases, we need to know about how light bounces off of a surface � This means knowing about the normal at the intersection point Remco Chang 10 – Lighting and Illumination 4/70

COMP 175 | COMPUTER GRAPHICS Normal Vectors at the Intersection Points �We discussed all three steps of Ray Casting �The key to Ray Casting is to do geometric computation in object coordinate space, but covert the results to world coordinate space. �One mathematical issue involves transforming the normal of a surface point from object coordinate space to world coordinate space… Remco Chang 10 – Lighting and Illumination 5/70

COMP 175 | COMPUTER GRAPHICS Computing Surface Normal (in Object Coordinate) � Remco Chang 10 – Lighting and Illumination 6/70

COMP 175 | COMPUTER GRAPHICS Normal Vector Transformed �We have a normal vector in object coordinate �We need a world-coordinate normal vector to compute the illumination model �How do we transform a point or a vector from the object coordinate to the world coordinate? � We apply the object’s transformation matrix M �Can we treat the normal the same way? � Answer: no… Remco Chang 10 – Lighting and Illumination 7/70

COMP 175 | COMPUTER GRAPHICS Normal Vector Transformed � Wrong! Mnobject Normal must be perpendicular nobject Remco Chang 10 – Lighting and Illumination 8/70

COMP 175 | COMPUTER GRAPHICS What Happened? � Why doesn’t this work? � Well, actually it does work for translation, rotation, and uniform scaling � nobject Let’s test it out… � Non-uniform scale causes a problem: � � The normal is distorted in exactly the opposite of what we want. Example below: Scale by 2 in x, 1 in y � Right Image: green line is what happens, but blue line is what the normal should be <0. 5, 0. 5> <0. 25, 0. 5> <1. 0, 0. 5> Remco Chang 10 – Lighting and Illumination 9/70

COMP 175 | COMPUTER GRAPHICS So How Do I Do This? � Remco Chang 10 – Lighting and Illumination 10/70

COMP 175 | COMPUTER GRAPHICS A More Rigorous Proof � Remco Chang 10 – Lighting and Illumination 11/70

COMP 175 | COMPUTER GRAPHICS A More Rigorous Proof � Remco Chang 10 – Lighting and Illumination 12/70

COMP 175 | COMPUTER GRAPHICS A More Rigorous Proof � Remco Chang 10 – Lighting and Illumination 13/70

COMP 175 | COMPUTER GRAPHICS Questions? Remco Chang 10 – Lighting and Illumination 14/70

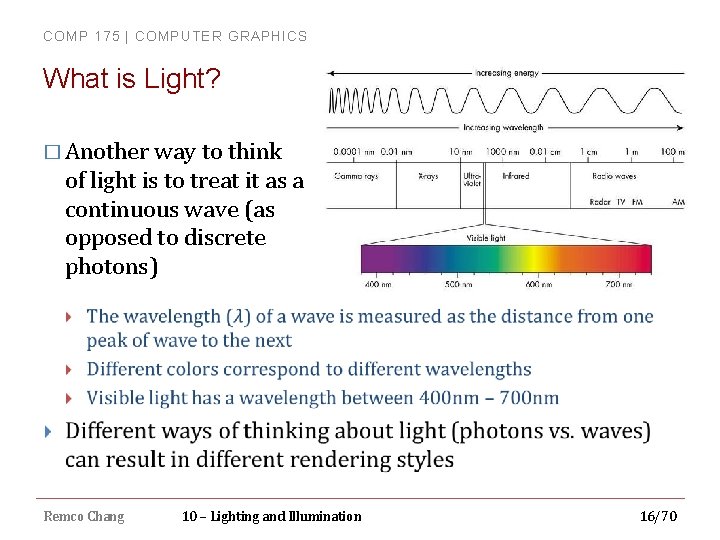
COMP 175 | COMPUTER GRAPHICS What is Light? � Can be thought of as small packets of photons When an electron drops from a higher level orbit to a lower orbit, energy is emitted as photons � Different energy levels of electrons allow for different wavelengths of light to be reflected � Metals have “loose” electrons, which can move relatively freely and occupy many different levels, which is why they are more reflective � Insulators have more constrained electrons which cannot change energy levels as easily, so they convert more absorbed light into heat instead of reflecting it � Remco Chang 10 – Lighting and Illumination 15/70

COMP 175 | COMPUTER GRAPHICS What is Light? � Another way to think of light is to treat it as a continuous wave (as opposed to discrete photons) Remco Chang 10 – Lighting and Illumination 16/70

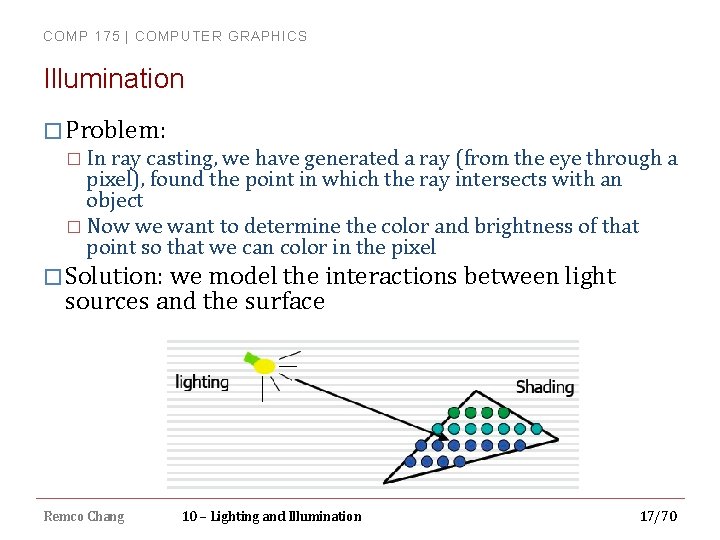
COMP 175 | COMPUTER GRAPHICS Illumination � Problem: � In ray casting, we have generated a ray (from the eye through a pixel), found the point in which the ray intersects with an object � Now we want to determine the color and brightness of that point so that we can color in the pixel � Solution: we model the interactions between light sources and the surface Remco Chang 10 – Lighting and Illumination 17/70

COMP 175 | COMPUTER GRAPHICS Illumination Models �An “illumination model” describes inputs, assumptions, and outputs used to calculate illumination (color / brightness) of surface elements � Usually includes � Light attributes (intensity, color, position, direction, shape) � Object surface properties (color, reflectivity, transparency, etc. ) � Interaction between lights and objects Remco Chang 10 – Lighting and Illumination 18/70

COMP 175 | COMPUTER GRAPHICS Illumination Models �Physically-based Illumination Models � Some models of illumination are based on real physics � Require accurate input data and make few assumptions � Rarely have enough information to specify all inputs � Takes a long time to compute �Non-Physically-Based Illumination Models � Just need a model that looks good enough for a specific application � Emphasis on speed and efficiency (use of resources like memory, CPU, etc. ) Remco Chang 10 – Lighting and Illumination 19/70

COMP 175 | COMPUTER GRAPHICS Light Attenuation: Inverse Square Law � The amount that a light illuminates an object decreases with the square of the distance between them. This is known as Light Attenuation. � Inverse square law: for a given 3 D angle (solid angle), the area it covers grows with the square of the distance � � Intensity of light per unit area falls off with the inverse square Conversely, for a fixed area, the angle it covers decreases with the square of the distance Remco Chang 10 – Lighting and Illumination 20/70

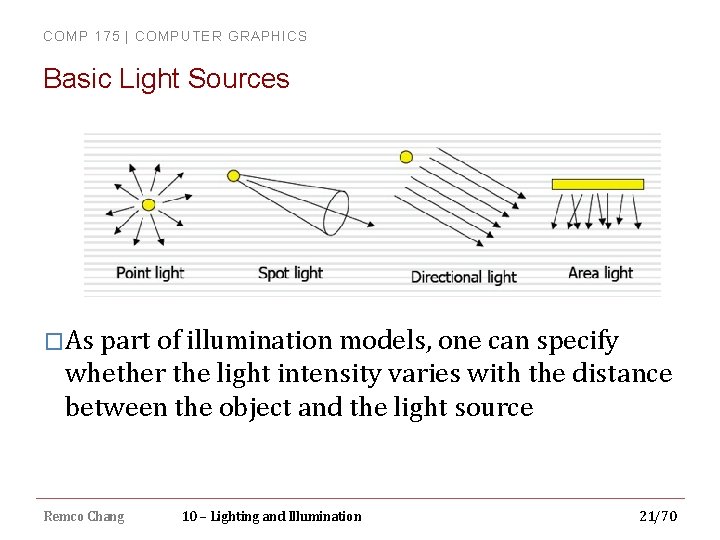
COMP 175 | COMPUTER GRAPHICS Basic Light Sources �As part of illumination models, one can specify whether the light intensity varies with the distance between the object and the light source Remco Chang 10 – Lighting and Illumination 21/70

COMP 175 | COMPUTER GRAPHICS Illumination Models � Local Illumination � Takes only direct lighting information � Is an approximation of global illumination � Usually involves the use of an “ambient” term to simulate indirect lighting � Global Illumination � Most light striking a surface element comes directly from a light emitting source (direct illumination) � Sometimes light from a source is blocked by another object, resulting in shadows � However, objects in the shadow can still receive light from light bouncing off other objects (indirect illumination) Remco Chang 10 – Lighting and Illumination 22/70

COMP 175 | COMPUTER GRAPHICS Example 1: Local Illumination �Only considers the light, the observer position, and the object’s material properties �Open. GL does this. Remco Chang 10 – Lighting and Illumination 23/70

COMP 175 | COMPUTER GRAPHICS Example 2: Global Illumination �Takes into account of the interaction of light from all the surfaces in the scene �Recursive ray tracing is an example. It models light rays bouncing between objects Remco Chang 10 – Lighting and Illumination 24/70

COMP 175 | COMPUTER GRAPHICS Example 3: Global Illumination, Radiosity �Models energy moving from emitters (light sources) into the scene as patches �Is view independent Remco Chang 10 – Lighting and Illumination 25/70

COMP 175 | COMPUTER GRAPHICS Examples of Global Illumination Direct illumination + specular reflection Ray trace Remco Chang + soft shadows and caustics Ray trace + caustic photon map 10 – Lighting and Illumination + diffuse reflection (color bleeding) Ray trace + caustic and diffuse photon maps 26/70

COMP 175 | COMPUTER GRAPHICS Questions? Remco Chang 10 – Lighting and Illumination 27/70

COMP 175 | COMPUTER GRAPHICS Simple Local Illumination (Phong) � Remco Chang 10 – Lighting and Illumination 28/70

COMP 175 | COMPUTER GRAPHICS Ambient Light Contribution �Ambient light = background light � As noted before, it is used to simulate indirect lighting �Ambient component � Independent of � Object’s position � Viewer’s position � Light source’s position � Dependent of � A constant factor (in each of the R, G, B channels) Remco Chang 10 – Lighting and Illumination 29/70

COMP 175 | COMPUTER GRAPHICS Diffuse Light Contribution �Diffuse light = illumination that a surface receives from a light source that reflects equally in all directions � Independent of: � Viewer’s position � Dependent of: � Light’s position � Surface property (normal, reflectance property) Remco Chang 10 – Lighting and Illumination 30/70

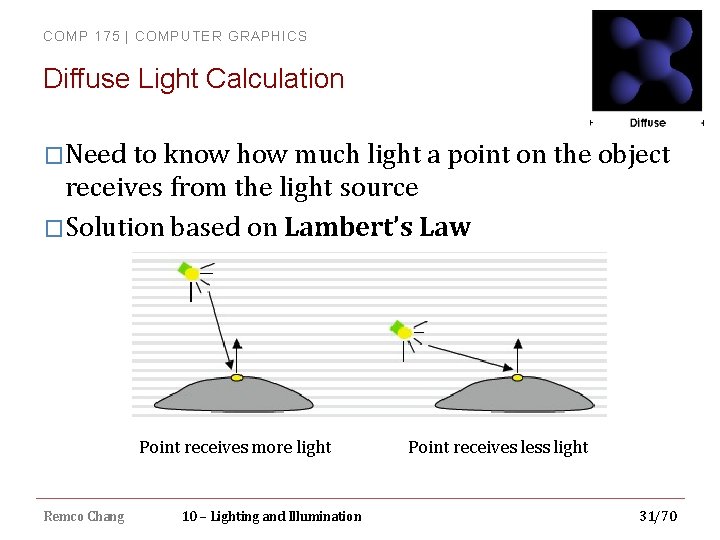
COMP 175 | COMPUTER GRAPHICS Diffuse Light Calculation �Need to know how much light a point on the object receives from the light source �Solution based on Lambert’s Law Point receives more light Remco Chang 10 – Lighting and Illumination Point receives less light 31/70

COMP 175 | COMPUTER GRAPHICS Diffuse Light Calculation � As the angle between the light and the normal increases, the light’s energy spreads across a larger area Remco Chang 10 – Lighting and Illumination The hemisphere represents equal magnitude of the reflected intensity for any outgoing vector. 32/70

COMP 175 | COMPUTER GRAPHICS Diffuse Light Examples � Remco Chang 10 – Lighting and Illumination 33/70

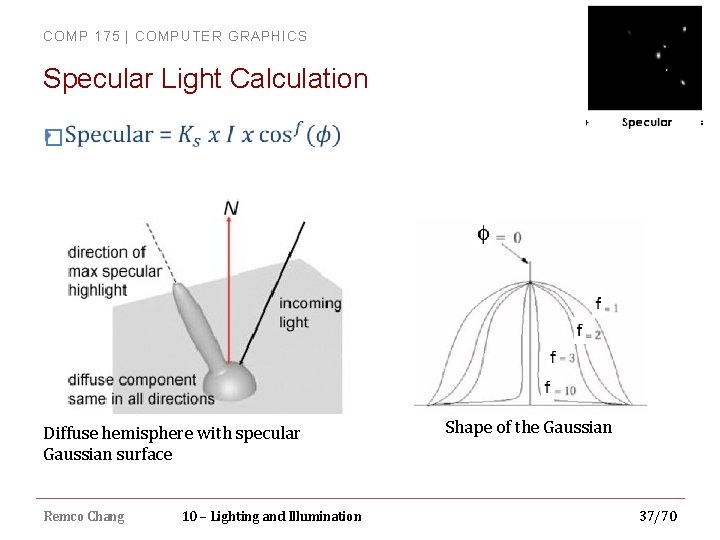
COMP 175 | COMPUTER GRAPHICS Specular Light Contribution � Specular light = light reflection from shiny surfaces � Color depends on material and how it scatters light � Shiny surfaces (metal, mirror, etc. ) reflect more light � Specular light depends on both light source position and view position Remco Chang 10 – Lighting and Illumination 34/70

COMP 175 | COMPUTER GRAPHICS Specular Light Calculation � Remco Chang 10 – Lighting and Illumination 35/70

COMP 175 | COMPUTER GRAPHICS Specular Light Calculation � Remco Chang 10 – Lighting and Illumination 36/70

COMP 175 | COMPUTER GRAPHICS Specular Light Calculation � Diffuse hemisphere with specular Gaussian surface Remco Chang 10 – Lighting and Illumination Shape of the Gaussian 37/70

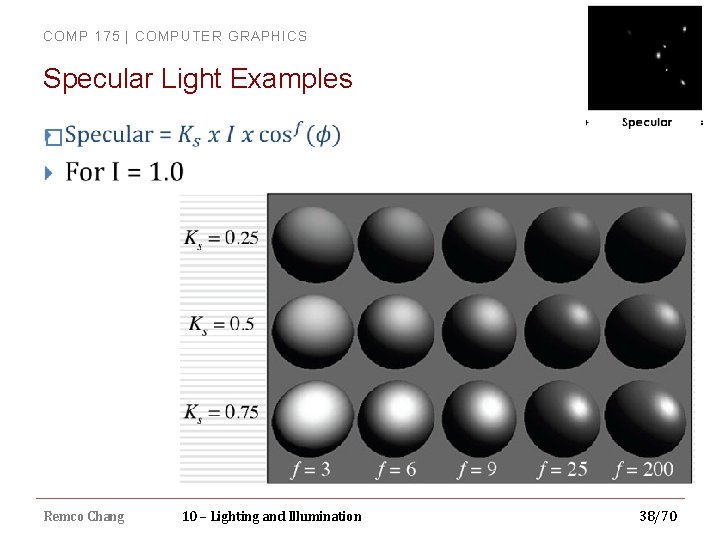
COMP 175 | COMPUTER GRAPHICS Specular Light Examples � Remco Chang 10 – Lighting and Illumination 38/70

COMP 175 | COMPUTER GRAPHICS Variation in Diffuse and Specular �Putting Diffuse and Specular together in our local illumination model Remco Chang 10 – Lighting and Illumination 39/70

COMP 175 | COMPUTER GRAPHICS Lighting Equation � Remco Chang 10 – Lighting and Illumination 40/70

COMP 175 | COMPUTER GRAPHICS Finding the Reflective Ray � Remco Chang 10 – Lighting and Illumination 41/70

COMP 175 | COMPUTER GRAPHICS Adding in Object Color � Remco Chang 10 – Lighting and Illumination 42/70

COMP 175 | COMPUTER GRAPHICS Debug Lighting Issues �Make sure that you normalize your normals!! � Since all calculations are based on surface normals (e. g. dot product with normals), if your normals are bad, you’re stuck. Remco Chang 10 – Lighting and Illumination 43/70

COMP 175 | COMPUTER GRAPHICS Summary: � Pseudocode for a non-recursive ray tracer: P = eye. Point for each pixel d = Compute Ray in World Coordinate for each object intersect P+td with object, record t and object Select object with smallest non-negative t value Find intersection point in Object Coordinate Compute normal of the point in Object Coordinate Transform normal to World Coordinate for each light Solve lighting equation in World Coordinate Set Pixel Color Remco Chang 10 – Lighting and Illumination 44/70

COMP 175 | COMPUTER GRAPHICS Questions? Remco Chang 10 – Lighting and Illumination 45/70

COMP 175 | COMPUTER GRAPHICS Shading vs. Lighting � How is Shading different from Lighting? � Lighting evaluates the lighting equation at each point on the surface of an object � Shading is kind of a “hack” that computes only lighting equations on the vertices, and interpolates the pixels in between Remco Chang 10 – Lighting and Illumination 46/70

COMP 175 | COMPUTER GRAPHICS Shading Models – Flat/Constant � We define a normal at each polygon (not at each vertex) � Lighting: Evaluate the lighting equation at the center of each polygon using the associated normal � Shading: Each sample point on the polygon is given the interpolated lighting value at the vertices (i. e. a total hack) Remco Chang 10 – Lighting and Illumination 47/70

COMP 175 | COMPUTER GRAPHICS Shading Models – Gouraud � We define a normal vector at each vertex � Lighting: Evaluate the lighting equation at each vertex using the associated normal vector � Shading: Each sample point’s color on the polygon is interpolated from the color values at the polygon’s vertices which were found in the lighting step Remco Chang 10 – Lighting and Illumination 48/70

COMP 175 | COMPUTER GRAPHICS Shading Models – Phong � Each vertex has an associated normal vector � Lighting: Evaluate the lighting equation at each vertex using the associated normal vector � Shading: For every sample point on the polygon we interpolate the normals at vertices of the polygon and compute the color using the lighting equation with the interpolated normal at each interior pixel Remco Chang 10 – Lighting and Illumination 49/70

COMP 175 | COMPUTER GRAPHICS Shading Models Compared Constant shading: no interpolation, pick a single representative intensity and propagate it over entire object. Loses almost all depth cues. Pixar “Shutterbug” images from: www. siggraph. org/education/materials/Hyper. Graph /scanline/shade_models/shading. htm Remco Chang 10 – Lighting and Illumination 50/70

COMP 175 | COMPUTER GRAPHICS Shading Models Compared Flat or Faceted Shading: constant intensity over each face Constant Shading Remco Chang 10 – Lighting and Illumination 51/70

COMP 175 | COMPUTER GRAPHICS Shading Models Compared Gouraud Shading: Linear Interpolation of intensity across triangles to eliminate edge discontinuity Flat Shading Remco Chang 10 – Lighting and Illumination 52/70

COMP 175 | COMPUTER GRAPHICS Shading Models Compared Phong Shading: Interpolation of vertex surface normals Note: specular highlights but no shadows. Still a pure local illumination model Gouraud Shading Remco Chang 10 – Lighting and Illumination 53/70

COMP 175 | COMPUTER GRAPHICS Shading Models Compared Global Illumination: Objects enhanced using shadow, texture, bump, and reflection mapping (see S 20) Phong Shading Remco Chang 10 – Lighting and Illumination 54/70

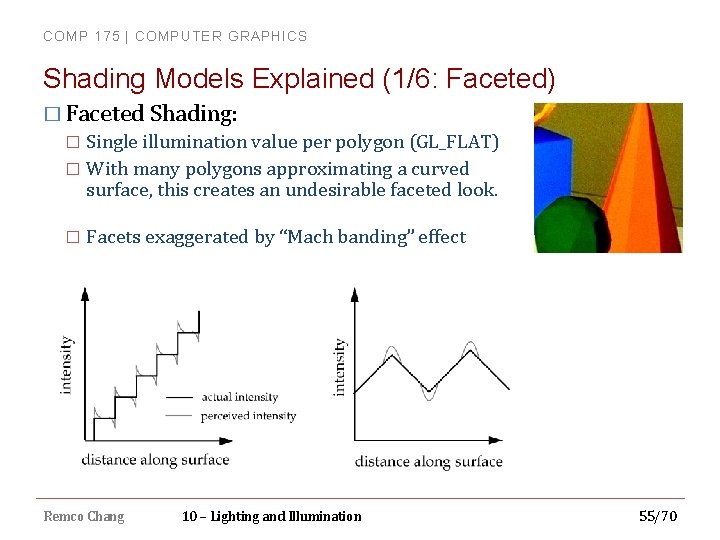
COMP 175 | COMPUTER GRAPHICS Shading Models Explained (1/6: Faceted) � Faceted Shading: Single illumination value per polygon (GL_FLAT) � With many polygons approximating a curved surface, this creates an undesirable faceted look. � � Facets exaggerated by “Mach banding” effect Remco Chang 10 – Lighting and Illumination 55/70

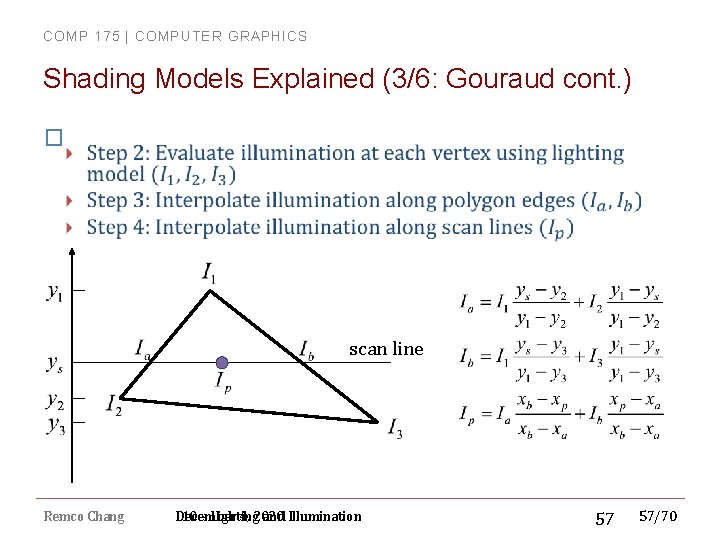
COMP 175 | COMPUTER GRAPHICS Shading Models Explained (2/6: Gouraud) � Illumination intensity interpolation (GL_SMOOTH) � � Illumination values are computed at vertices, linearly interpolated across the pixels of the polygon Eliminates intensity discontinuities at polygon edges; still have gradient discontinuities, Mach banding is largely ameliorated, not eliminated Must differentiate desired creases from tesselation artifacts (edges of cube vs. edges on tesselated sphere) Step 1: Compute vertex normals by averaging surrounding polygon normals Remco Chang 10 – Lighting and Illumination 56/70

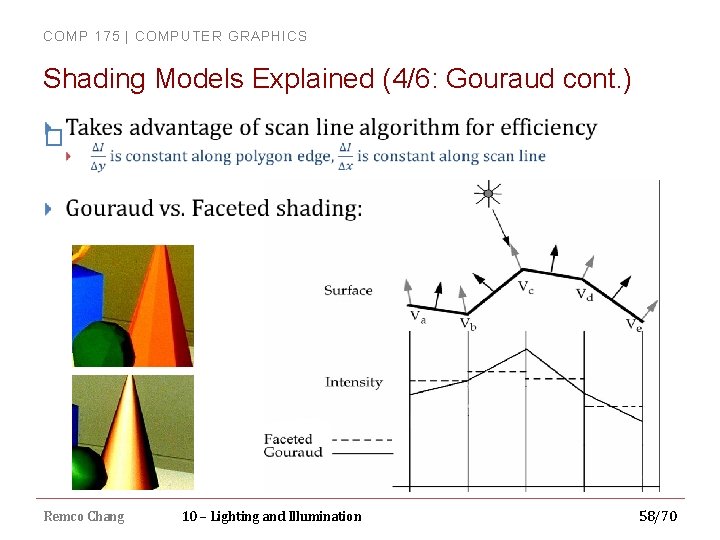
COMP 175 | COMPUTER GRAPHICS Shading Models Explained (3/6: Gouraud cont. ) � scan line Remco Chang December 4, 2020 10 – Lighting and Illumination 57 57/70

COMP 175 | COMPUTER GRAPHICS Shading Models Explained (4/6: Gouraud cont. ) � Remco Chang 10 – Lighting and Illumination 58/70

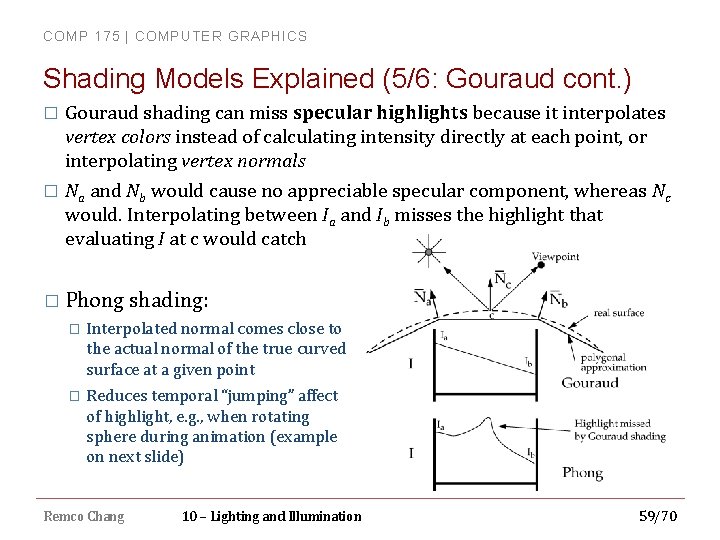
COMP 175 | COMPUTER GRAPHICS Shading Models Explained (5/6: Gouraud cont. ) Gouraud shading can miss specular highlights because it interpolates vertex colors instead of calculating intensity directly at each point, or interpolating vertex normals � Na and Nb would cause no appreciable specular component, whereas Nc would. Interpolating between Ia and Ib misses the highlight that evaluating I at c would catch � � Phong shading: � Interpolated normal comes close to the actual normal of the true curved surface at a given point � Reduces temporal “jumping” affect of highlight, e. g. , when rotating sphere during animation (example on next slide) Remco Chang 10 – Lighting and Illumination 59/70

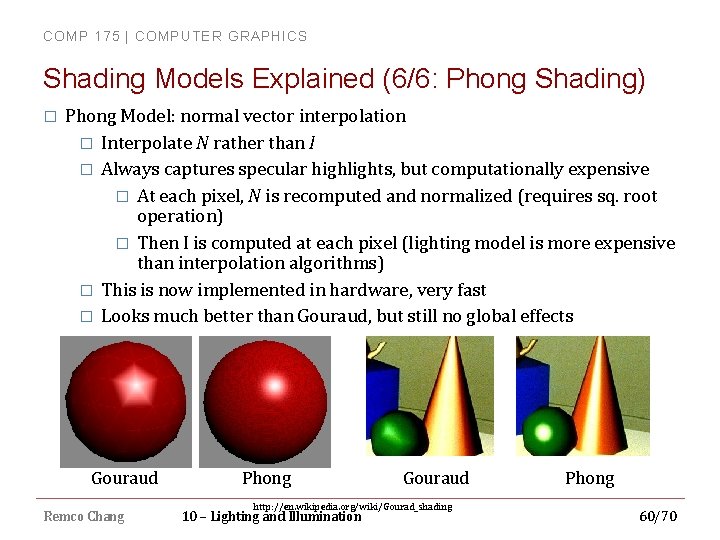
COMP 175 | COMPUTER GRAPHICS Shading Models Explained (6/6: Phong Shading) � Phong Model: normal vector interpolation � Interpolate N rather than I � Always captures specular highlights, but computationally expensive � At each pixel, N is recomputed and normalized (requires sq. root operation) � Then I is computed at each pixel (lighting model is more expensive than interpolation algorithms) � This is now implemented in hardware, very fast � Looks much better than Gouraud, but still no global effects Gouraud Remco Chang Phong Gouraud http: //en. wikipedia. org/wiki/Gourad_shading 10 – Lighting and Illumination Phong 60/70

COMP 175 | COMPUTER GRAPHICS Gouraud vs. Phong Shading Remco Chang 10 – Lighting and Illumination 61/70

COMP 175 | COMPUTER GRAPHICS Additional Material Remco Chang 10 – Lighting and Illumination 62/70

COMP 175 | COMPUTER GRAPHICS Using Halfway Vector for Speed (Blinn-Phong) n n � Remco Chang 10 – Lighting and Illumination 63/70

COMP 175 | COMPUTER GRAPHICS Lighting Equation Using Halfway Vector � Remco Chang 10 – Lighting and Illumination 64/70

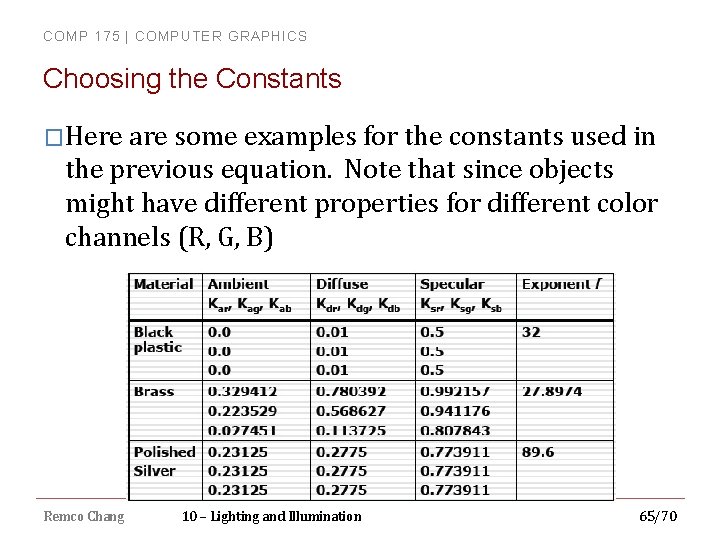
COMP 175 | COMPUTER GRAPHICS Choosing the Constants �Here are some examples for the constants used in the previous equation. Note that since objects might have different properties for different color channels (R, G, B) Remco Chang 10 – Lighting and Illumination 65/70

COMP 175 | COMPUTER GRAPHICS Lights in Open. GL �This would have been useful for your Scene. View assignment… �Defining lights: Remco Chang 10 – Lighting and Illumination 66/70

COMP 175 | COMPUTER GRAPHICS Lights in Open. GL �Setting the light position as (0, 0, 1, 1) means that the light is a point light. Setting the light position as (0, 0, 1, 0) means that the light is a directional light (infinite light) �Enable lighting, you need to do both: � gl. Enable (GL_LIGHTING); � gl. Enable (GL_LIGHT 0); // for light 0. Light 1 for light 1, etc. Remco Chang 10 – Lighting and Illumination 67/70

COMP 175 | COMPUTER GRAPHICS Materials in Open. GL �Material Example: Remco Chang 10 – Lighting and Illumination 68/70

COMP 175 | COMPUTER GRAPHICS Birectional Reflectance Distribution Function (BRDF) � specular reflection (big) in nt de ci diffuse reflections ht lig am be surface Remco Chang 10 – Lighting and Illumination reflected scatter distribution BRDF Image credit: © Ben Herila, 2010 69/70

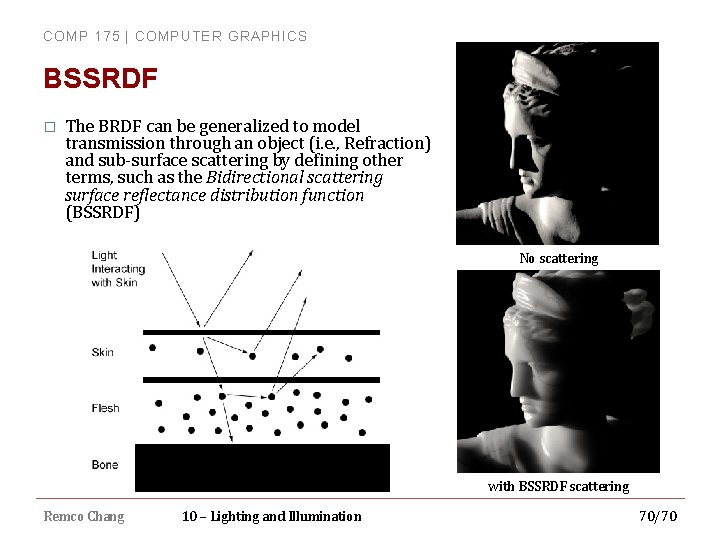
COMP 175 | COMPUTER GRAPHICS BSSRDF � The BRDF can be generalized to model transmission through an object (i. e. , Refraction) and sub-surface scattering by defining other terms, such as the Bidirectional scattering surface reflectance distribution function (BSSRDF) No scattering with BSSRDF scattering Remco Chang 10 – Lighting and Illumination 70/70

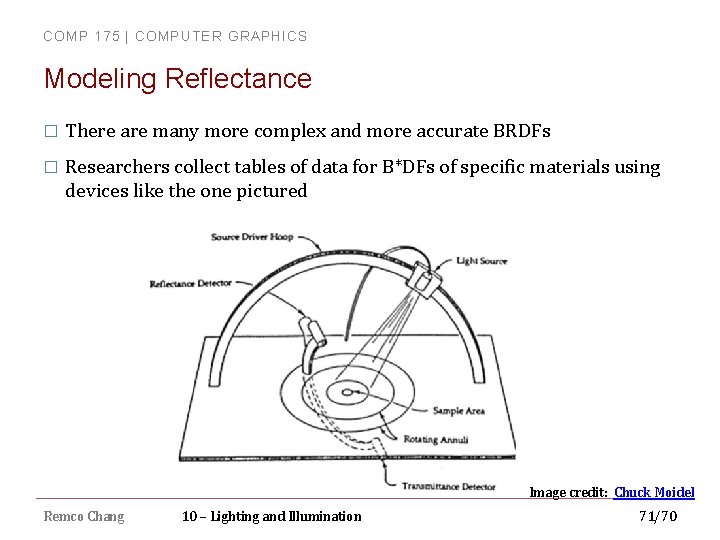
COMP 175 | COMPUTER GRAPHICS Modeling Reflectance � There are many more complex and more accurate BRDFs � Researchers collect tables of data for B*DFs of specific materials using devices like the one pictured Image credit: Chuck Moidel Remco Chang 10 – Lighting and Illumination 71/70

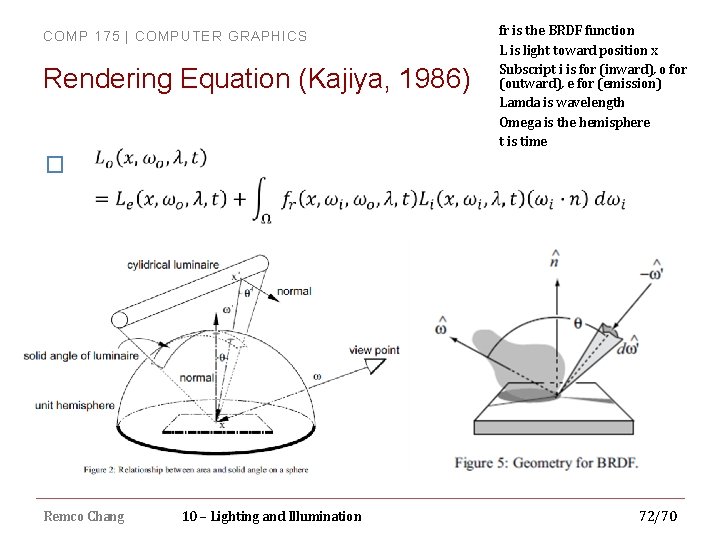
COMP 175 | COMPUTER GRAPHICS Rendering Equation (Kajiya, 1986) � Remco Chang 10 – Lighting and Illumination fr is the BRDF function L is light toward position x Subscript i is for (inward), o for (outward), e for (emission) Lamda is wavelength Omega is the hemisphere t is time 72/70

COMP 175 | COMPUTER GRAPHICS Rendering Equation (Kajiya, 1986) � Remco Chang 10 – Lighting and Illumination 73/70

COMP 175 | COMPUTER GRAPHICS Questions? Remco Chang 10 – Lighting and Illumination 74/70