COMP 1321 Digital Infrastructure Richard Henson University of

COMP 1321 Digital Infrastructure Richard Henson University of Worcester October 2012

Week 4: Motherboards n Learning Objectives: ØExplain main purpose of the motherboard ØExplain how a CPU can handle input & output from slow & fast devices ØExplain how motherboard architecture has changed in response to miniaturisation, energy-saving, and consumerisation demands

Why a Motherboard? n CPU far too fragile to exist independently Ø i. e. needs a “mother” n motherboard delivers power and control to CPU via Ø control bus Ø timing chips Ø ROM and RAM n harnesses power of CPU effectively so it can interact effectively with i/o devices

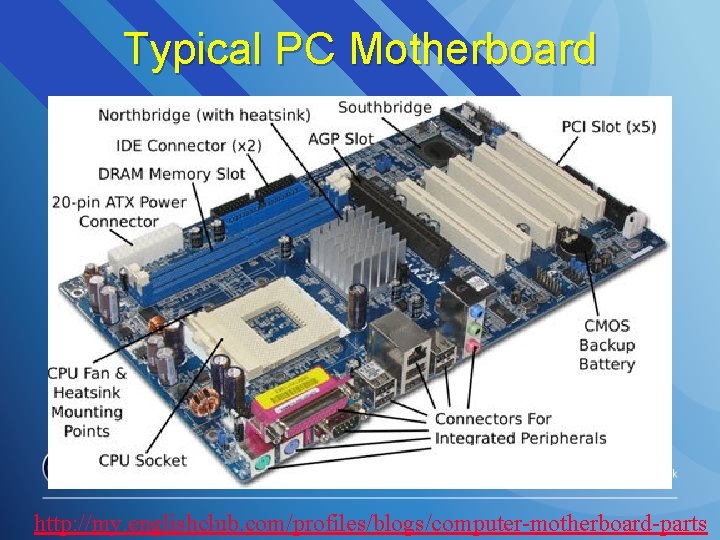
Typical PC Motherboard http: //my. englishclub. com/profiles/blogs/computer-motherboard-parts

I/O devices sorted by data transfer times Joystick Keyboard Mouse CD Rom TV Camera Audio IDE HDD Scanner VDU 10 B/s 100 B/s 1 k. B/s 100 k. B/s 1 MB/s 100 MB/s

Typical Slow devices Keyboard n Mouse n Joystick n Audio n

Fast devices (connect straight into motherboard) VDU n Hard drive n CD-ROM n Scanner n

Even faster devices. . CPU n Memory (static/dynamic RAM & ROM) n Graphics processors (GPU) n

i/o Connectors n Slow (off motherboard via ports) Ø Serial Ø Parallel Ø Firewire Ø PS/2 mouse & keyboard (legacy) Ø VGA Ø RJ-45: Network connection Ø USB: getting faster & becoming the standard

Motherboard connectors from http: //www. techiwarehouse. com/cms/articles. php? cat=13

North Bridge & South Bridge n North: control chipset for fastest onboard devices Ø ROM & static RAM n South: control chipset for slower onboard devices Ø SATA & IDE connectors » hard disk & CD-ROM/DVD Ø RAM connectors » many types, differing no. of pins

Layout of component connections Extremely fast components talking directly to each other “North Bridge” chipset Connection Fast components talking directly to each other “South Bridge” chipset Connection Slow components talking directly to each other

Buffers Areas of memory/storage where data is stored before forwarding n Message from slow device received and stored in buffer n Øthen sent quickly to fast device n Message from fast devices stored Øthen sent slowly to slow device

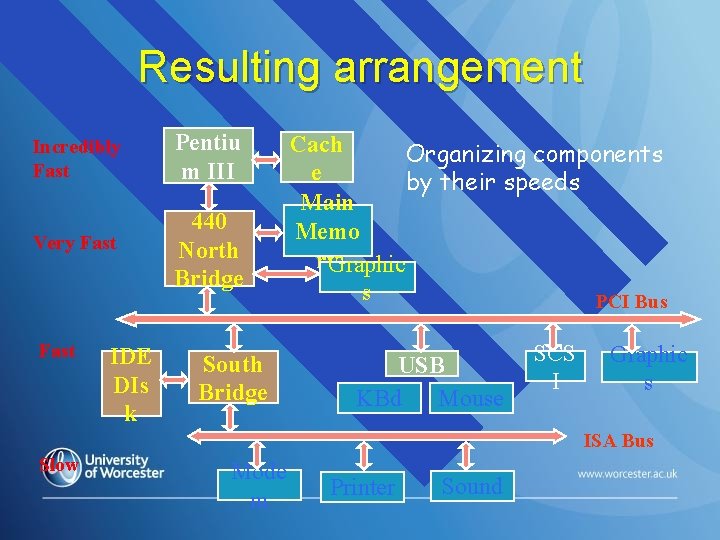
Resulting arrangement Incredibly Fast Pentiu m III Very Fast 440 North Bridge Fast IDE DIs k South Bridge Cach Organizing components e by their speeds Main Memo ry. Graphic s PCI Bus USB KBd Mouse SCS I Graphic s ISA Bus Slow Mode m Printer Sound

Buses and on-board communications Bus - physical link between computer components that electrical impulses (ie data as 0 s and 1 s) can travel through n Only one device can send a message at any one time n Øother devices have to wait until the line is clear before sending

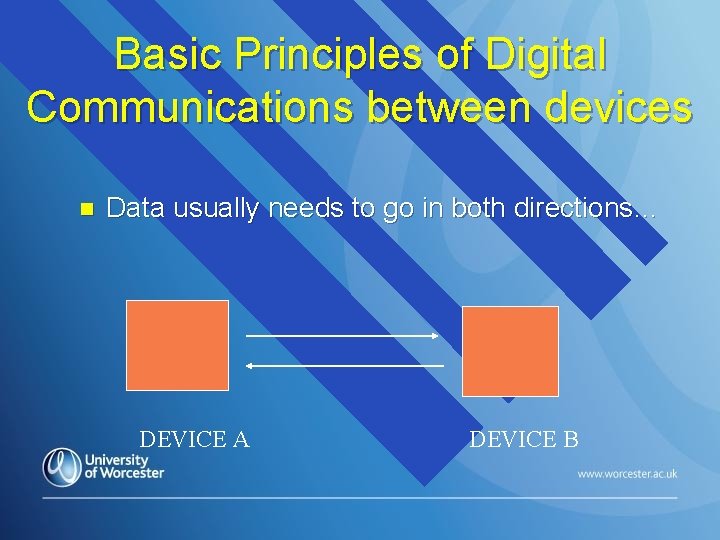
Basic Principles of Digital Communications between devices n Data usually needs to go in both directions… DEVICE A DEVICE B

The Three Data Communication Alternatives n Simplex Ø or one direction only n Example: Ø Broadcast data from a radio or TV mast

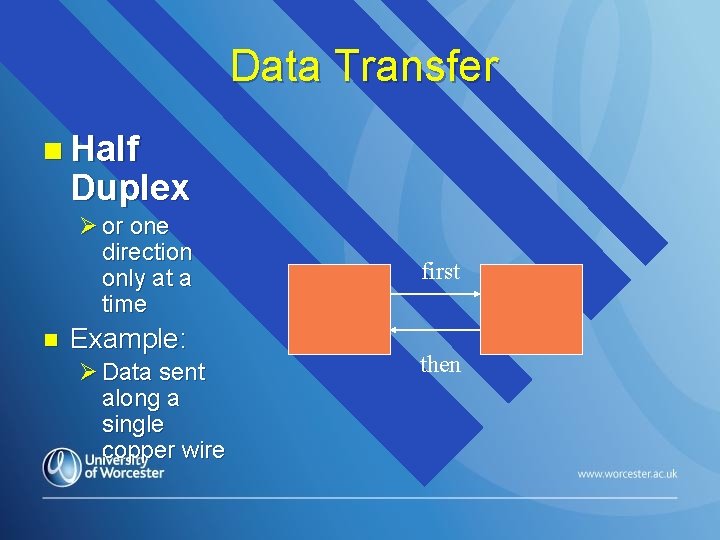
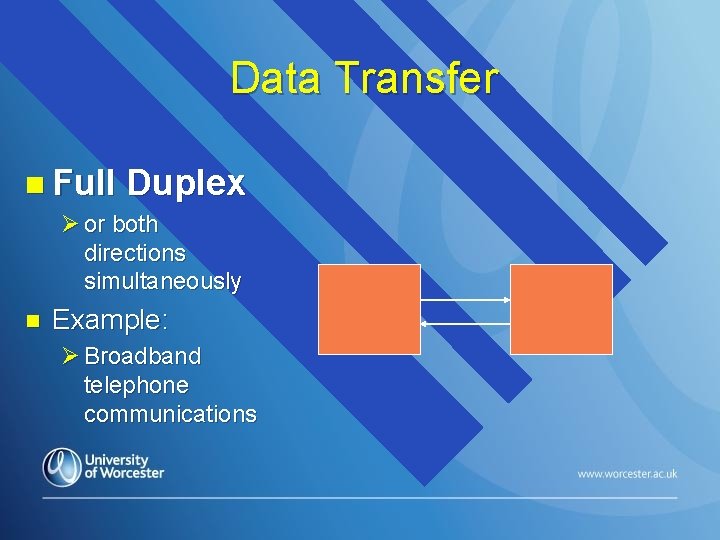
Data Transfer n Half Duplex Ø or one direction only at a time n Example: Ø Data sent along a single copper wire first then

Data Transfer n Full Duplex Ø or both directions simultaneously n Example: Ø Broadband telephone communications

i/o connections with the motherboard n Normally connect digital i/o devices to the motherboard via: ØDirect connections through “ports” ØClick in expansion or “daughter” cards with their own ports

i/o Buses used with older expansion Cards n ISA = Industry Standard Association Ø early (1981 -1984) communications standard between PC components Ø speed: up to 16 MB s-1 Ø 8 or 16 -bit parallel connections n PCI = Peripheral Component Interconnect Ø later (1990 -1993) communications standard between computer components Ø speed: up to 133 MB s-1 Ø 32 -bit parallel connection Ø ‘Plug and play’ – no set-up software needed, (depending on the operating system used…)

Older Motherboard: PCI & ISA slots from http: //www. ibase-i. com. tw/mb 700 pixel 600. jpg PCI slot ISA slot

Peripheral Connectors on the Motherboard n On-board IDE slot Øconnects up to TWO hard disk drives, floppy disk drives, CD-ROM drives, DVD-ROM drives directly to the motherboard n On-board SCSI slot Øconnects a much larger number of devices as above to the motherboard

More modern arrangement n Idea copied from “star” arrangement for networking computers together: (see later) Øa “hub” connects components of similar speed » hub at centre; components at ends of ‘spokes’ Øthe several hubs communicate directly with each other

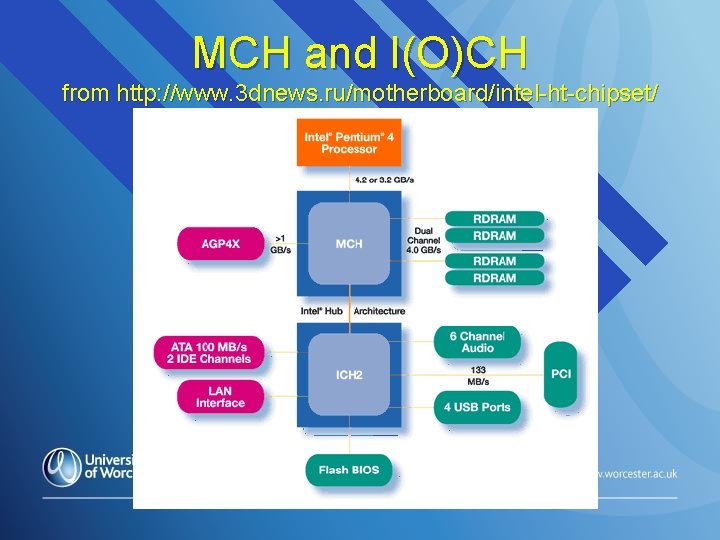
Motherboard Hubs n MCH = Memory Control Hub Øconnects very fast devices together in a ‘star’ configuration n I(O)CH = Input-output Control Hub Øconnects together slower devices, also in a star configuration n MCH communicates directly with I(O)CH

MCH and I(O)CH from http: //www. 3 dnews. ru/motherboard/intel-ht-chipset/

Motherboard with MCH and ICH from http: //www. tomshardware. com/motherboard/20040712/i 865 -i 875 -mobos 21. html MCH ICH

Why are motherboard components arranged this way? n Longer wires… Ømore time to send messages (good) Ødegradation of message at high speed (bad) n Therefore… Øimportant for fast components to be close together Øslower components can be further apart

Motherboard with MCH and ICH from http: //www. tomshardware. com/motherboard/20040712/i 865 -i 875 -mobos 21. html AGP slot Socket for processor MCH ICH Slots for RAM cards

Another PC Motherboard… from http: //www. techiwarehouse. com/cms/articles. php? cat=13

Motherboard & expansion board from http: //www. answers. com/topic/motherboard

Smaller Motherboards n So far… Øconsidered Intel 8086 series CPU Ølarge instruction set & power requirements n Other CPUs use much less power, smaller instruction set Øtherefore motherboard requirements miniaturised » e. g. Intel Atom: Netbook & Tablet PCs » ARM: Smartphones & Tablets

Motherboard-on-a-chip Started with Smartphones n Spread to Tablet PCs… n

Architecture of Motherboard chip n With further miniaturisation… Ø“motherboard” self-contained » mounted on a board to provide i/o connectors

Arduino Board (i/o) n Microcontroller… not “motherboard on a chip” Ø therefore not expensive. . n Based on i/o control, not apps Ø used for “physical” computing (real devices) » http: //www. atmel. com/Images/doc 8161. pdf Ø EPROM for embedded programming (“C”) Ø USB-computer for power (a few m. A) Ø USB provides scope to use i/o for many purposes http: //www. ladyada. net/learn/arduino/lesson 3. html

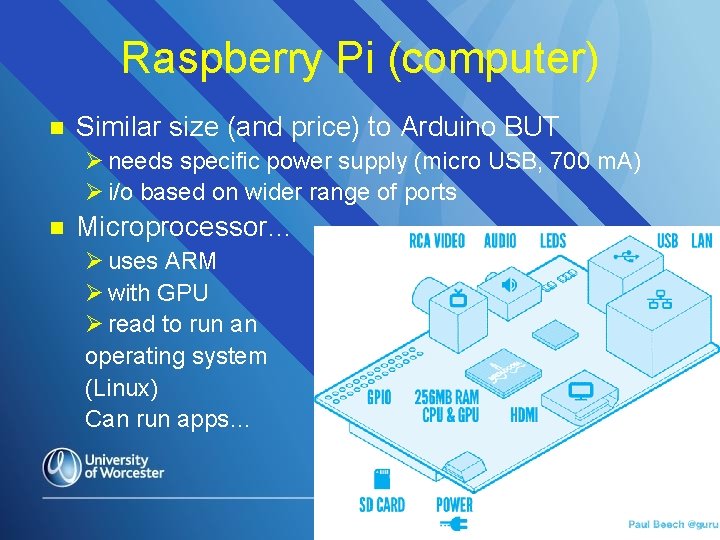
Raspberry Pi (computer) n Similar size (and price) to Arduino BUT Ø needs specific power supply (micro USB, 700 m. A) Ø i/o based on wider range of ports n Microprocessor… Ø uses ARM Ø with GPU Ø read to run an operating system (Linux) Can run apps…