COMP 103 FASTER SORTING using RECURSION QUICKSORT 2

COMP 103 FASTER SORTING using RECURSION : QUICKSORT

2 RECAP-TODAY Merge. Sort analysis (How do you analyse recursive algorithms? ) Quick. Sort The Mid-term Test on Monday 30 th of April at 11 am (during normal lecture slot) THE ROOMS ARE ANNOUNCED ON THE WEB SITE!!! please bring Student ID card, sit in alternate rows & alternate seats practice on previous tests (via “previous tests & exams” on sidebar) any material up to this point (end of today) could be tested GOOD LUCK!

3 Divide and Conquer Sorts To Sort: Array Split Sort each part (recursive) Combine Where does the work happen? Sub. Array Split Sort Sub. Array Sort Sorted. Sub. Array Combine Sorted. Sub. Array split is trivial combine does all the work Quick. Sort: Sub. Array Split Merge. Sort: Split split does all the work combine is trivial Combine Sorted Array

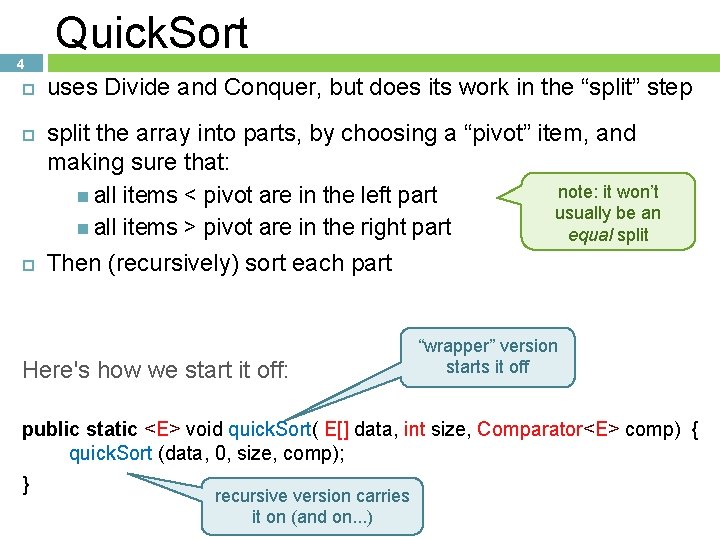
4 Quick. Sort uses Divide and Conquer, but does its work in the “split” step split the array into parts, by choosing a “pivot” item, and making sure that: note: it won’t all items < pivot are in the left part usually be an all items > pivot are in the right part equal split Then (recursively) sort each part Here's how we start it off: “wrapper” version starts it off public static <E> void quick. Sort( E[] data, int size, Comparator<E> comp) { quick. Sort (data, 0, size, comp); } recursive version carries it on (and on. . . )

Quick. Sort – the recursion 5 public static <E> void quick. Sort(E[ ] data, int low, int high, Comparator<E> comp){ if (high-low < 2) // only one item to sort. return; if (high - low < 4) // only two or three items to sort 3(data, low, high, comp); else { // split into two parts, mid = index of boundary int mid = partition(data, low, high, comp); quick. Sort(data, low, mid, comp); quick. Sort(data, mid, high, comp); } } 0 1 2 3 4 5 6 7 8 9 10 11

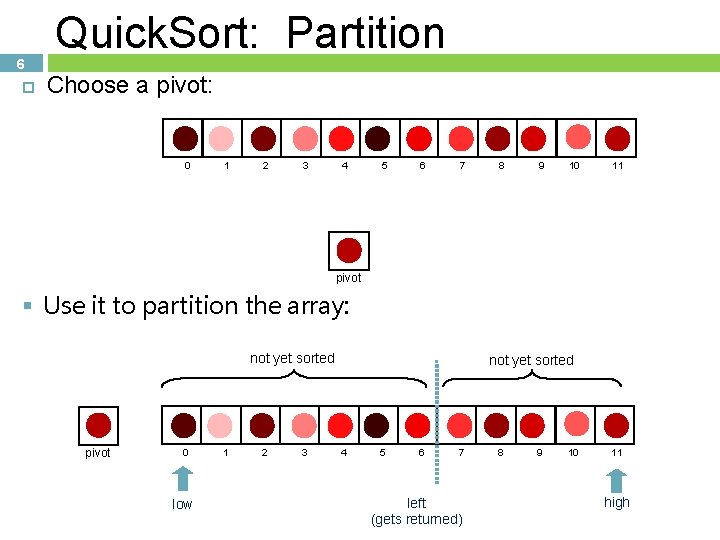
6 Quick. Sort: Partition Choose a pivot: 0 1 2 3 4 5 6 7 8 9 10 11 pivot § Use it to partition the array: not yet sorted pivot 0 low 1 2 3 not yet sorted 4 5 6 7 left (gets returned) 8 9 10 11 high

7 Quick. Sort: Partition /** Partition into small items (low. . mid-1) and large items (mid. . high-1) private static <E> int partition(E[] data, int low, int high, Comparator<E> comp){ data[low]; //data[high-1], simple but poor choice! median(data[low], data[(low+high)/2], comp); E pivot = int left = low-1; int right = high; while( left <= right ){ do { left++; // just skip over items on the left < pivot } while (left<high &&compare(data[left], pivot)< 0); do { right--; // just skip over items on the right > pivot } while (right>=low && compare(data[right], pivot)> 0); if (left < right) swap(data, left, right); } return left; } 0 1 2 3 4 5 6 7 8 9 10 11

8 Quick. Sort data array : [p indexes : [0 a 1 r 1 2 f 3 e 4 q 2 w 5 6 q 1 t 7 8 z 2 x c v b z 1 a 2 ] 9 10 11 12 13 14 15 ] do 0. . 16 part@p ->6 do 0. . 6 part@c ->4 do 0. . 4 part@b ->3 do 0. . 3 done 0. . 3 do 3. . 4 done 0. . 4 do 4. . 6 done 0. . 6 do 6. . 16 part@q 2 ->8 do 6. . 8 done 6. . 8 a 1 a 1 f f f c c c e e q 2 w c f q 1 t z 2 x c v q 2 v b r e e e f f f q 1 t q 2 q 2 z 2 x q 2 v q 1 v r r : : : : : [p [a 2 [a 2 [ [ [a 2 [ [ r b b b b a 1 b c c c w p p p z 1 a 2 ] z 1 p ] ] ] z 1 p ] z 1 w ] ] ]

9 Quick Sort do 6. . 16 : part@q 2 ->8 : do 6. . 8 : done 6. . 8 : do 8. . 16 : part@v ->12: do 8. . 12 : part@t ->10: do 8. . 10 : done 8. . 10 : do 10. . 12: done 8. . 12 : do 12. . 16: part@x ->13: do 12. . 13: do 13. . 16: done 12. . 16: done 8. . 16 : done 6. . 16 : done 0. . 16 : [ [ [ [ [ [a 2 a 1 b w p p p q 1 t q 2 q 2 t t t q 1 q 1 z 2 x q 2 v q 1 v r r z 2 r r r x v v v q 1 x q 1 t r z 1 w z 2 z 1 w v t t t v v q 1 r x w w c e f p p q 1 r q 2 q 1 r t t t v v v w w z 1 p z 1 w z 2 z 1 x z 2 x x x z 1 z 2 z 2 z 2 x z 1 z 1 z 1 ] ] ] ] ] ]

10 Quick. Sort public static <E> void quick. Sort (E[ ] data, int low, int high, Comparator<E> comp) { if (high > low +2) { int mid = partition(data, low, high, comp); quick. Sort(data, low, mid, comp); quick. Sort(data, mid, high, comp); } } Cost of Quick Sort: three steps: partition: has to compare (high-low) pairs first recursive call second recursive call

11 Quick. Sort Cost: If Quicksort divides the array exactly in half, then: C(n) = n + 2 C(n/2) n log(n) comparisons = O(n log(n)) (best case) If Quicksort divides the array into 1 and n-1: C(n) = n + (n-1) + (n-2) + (n-3) + … + 2 + 1 = n(n-1)/2 comparisons = O(n 2) (worst case) Average case? very hard to analyse. still O(n log(n)), and very good. Quicksort is “in place”, Merge. Sort is not

12 Stable or Unstable? Faster if almostsorted? Merge. Sort: Stable: doesn’t jump any item over an unsorted region ⇒ two equal items preserve their order Same cost on all input “natural merge” variant doesn’t sort already sorted regions ⇒ will be very fast: O(n) on almost sorted lists Quick. Sort: Unstable: Partition “jumps” items to the other end ⇒ two equal items likely to reverse their order Cost depends on choice of pivot. simplest choice is very slow: O(n 2) even on almost sorted lists better choice (median of three) ⇒ O(n log(n)) on almost sorted lists

13 Some Big-O costs revisited Implementing Collections: Array. List: O(n) to add/remove, except at end Stack: O(1) Array. Set: O(n) Sorted. Array. Set O( log(n) ) to search O(n) to add/remove (cost of searching) (with binary search) (cost of moving up/down) O( n 2 ) to add n items O( n log(n) ) to initialise with n items. (with fast sorting)

14 Quick Review of Topics (for Test) Using Collections (List, Set, Map, Bag, Stack, Queue…. ) Interfaces, Abstracts. Classes, Classes (extends and implements) Iterator, Iterable, Comparator, Comparable Implementing Collections (Array. List, Sorted. Array. Bag, Array. Set…) Recursion Sorting (Selection, Insertion, Merge. Sort, Quick. Sort…. ) Cost analysis (“Big-O” notation and calculation…