COMMUTATORS ROBUSTNESS and STABILITY of SWITCHED LINEAR SYSTEMS

COMMUTATORS, ROBUSTNESS, and STABILITY of SWITCHED LINEAR SYSTEMS Daniel Liberzon Univ. of Illinois at Urbana-Champaign, U. S. A. Joint work with Yuliy Baryshnikov SIAM Conference on Control & its Applications, Paris, July 2015 1 of 12

SWITCHED SYSTEMS Switched system: • • is a family of systems is a switching signal Switching can be: • State-dependent or time-dependent • Autonomous or controlled Details of discrete behavior are “abstracted away” Discrete dynamics classes of switching signals Properties of the continuous state : stability 2 of 12

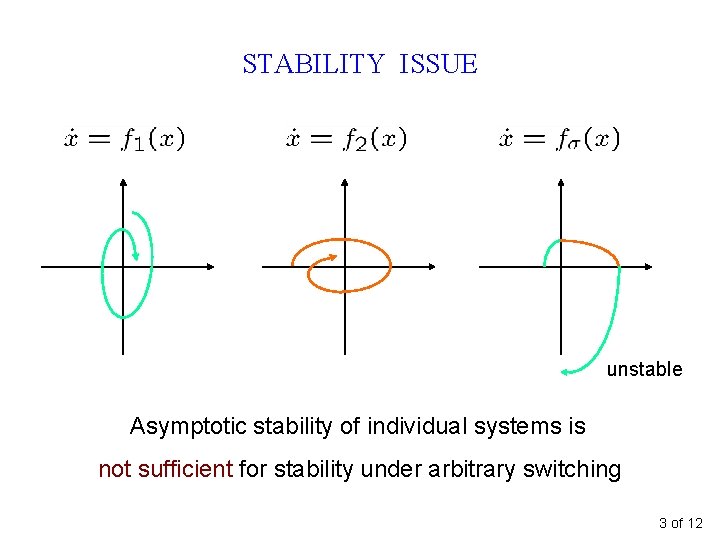
STABILITY ISSUE unstable Asymptotic stability of individual systems is not sufficient for stability under arbitrary switching 3 of 12

COMMUTING STABLE MATRICES => GUES Switched linear system: (commuting Hurwitz matrices) For matrices – similarly 4 of 12

COMMUTING STABLE MATRICES => GUES Alternative proof: quadratic common Lyapunov function [Narendra–Balakrishnan ’ 94] . . . is a common Lyapunov function 5 of 12

SUMMARY of KNOWN RESULTS Lie algebra w. r. t. Stability is preserved under arbitrary switching for: • commuting matrices: • nilpotent Lie algebras (suff. high-order Lie brackets are 0) e. g. • solvable Lie algebras (triangular up to coord. transf. ) • solvable + compact (purely imaginary eigenvalues) Quadratic common Lyapunov function exists in all these cases No further extension based on Lie algebra only [Narendra–Balakrishnan, Gurvits, Kutepov, L–Hespanha–Morse, Agrachev–L] 6 of 12

REMARKS on LIE-ALGEBRAIC CRITERIA • Checkable conditions • In terms of the original data • Independent of representation • Not robust to small perturbations In any neighborhood of any pair of matrices there exists a pair of matrices generating the entire Lie algebra How to capture closeness to a “nice” Lie algebra? 7 of 12

ALMOST COMMUTING vs. NEAR COMMUTING Halmos’s problem (1976): is a pair of (self-adjoint) matrices which almost commute always close to a pair of commuting matrices? • Pearcy–Shields (1978): positive result, one matrix must be self-adjoint • Exel–Loring (1978): counterexample, uses unitary matrices of growing dimension • Lin (1997): positive result for self-adjoint matrices with bounded norm • Kachkovskiy–Safarov (2014): quantitative bound for Lin’s theorem • Łojasiewicz (1978): general theorem relating the value of a function to the distance to its zero set • Ji–Kollar–Shiffman (1992): more specific Łojasiewicz bounds for polynomials or maxima of finitely many polynomials • Hastings–Loring (2010): Łojasiewicz-type bounds for self-adjoint and unitary matrices with bounded norm 8 of 12

ŁOJASIEWICZ INEQUALITY real analytic function – zero set of Then for every compact, Meaning: if then s. t. When is a maximum of finitely many polynomials, explicit bounds on the exponent can be obtained 9 of 12

ŁOJASIEWICZ APPLIED TO OUR SET – UP – finite set of Hurwitz matrices Suppose where is Frobenius norm Let This is max of coefficients of polynomials of degree 4 in (or can use sum to get a single polynomial) Let be distance from to nearest -tuple of pairwise commuting matrices (Frobenius norm of difference between stacked matrices) Łojasiewicz inequality gives i. e. , with Higher-order commutators (near nilpotent / solvable) – similar 10 of 12

PERTURBATION ANALYSIS commute (or generate nilpotent or solvable Lie algebra) common Lyapunov function For original matrices: which is still negative definite if stability of is ensured if For commuting and solvable cases, specific known constructions of can be used to estimate the right-hand side [Baryshnikov–L, CDC ’ 13] depend on (# of matrices) and on compact set where they live can be explicitly estimated estimating is a bit more difficult [Ji–Kollar–Shiffman] 11 of 12

CONCLUSIONS Results: • Qualitative: switched linear system remains stable if commutation relations are only approximately satisfied • Asymptotic: admissible commutator size goes to 0 at rate of stability margin raised to power • Quantitative: explicit estimates are possible in principle, but checking LMI feasibility is probably more numerically efficient Open questions: • Relation to approach in [Agrachev–Baryshnikov–L, SCL, 2012] • Compact but infinite matrix families (trade-off between and ) • Switched nonlinear systems (e. g. polynomial) 12 of 12