Community Detection in Graphs Networks Communities We often

Community Detection in Graphs

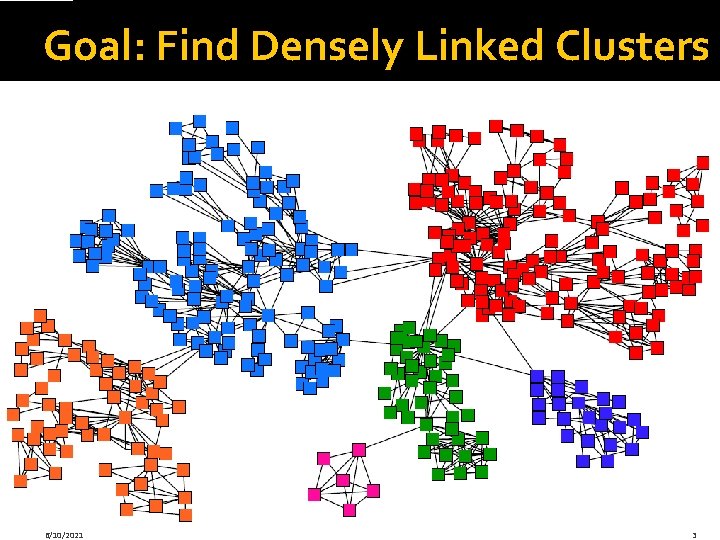
Networks & Communities �We often think of networks being organized into modules, cluster, communities: 6/10/2021 2

Goal: Find Densely Linked Clusters 6/10/2021 3

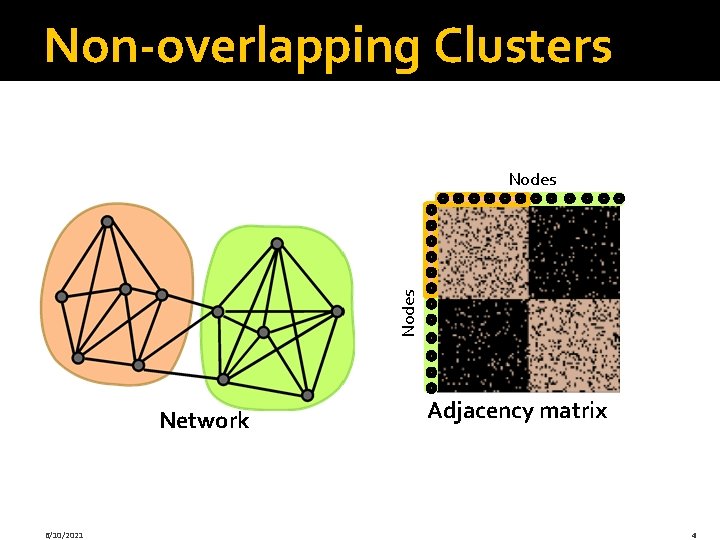
Non-overlapping Clusters Nodes Network 6/10/2021 Adjacency matrix 4

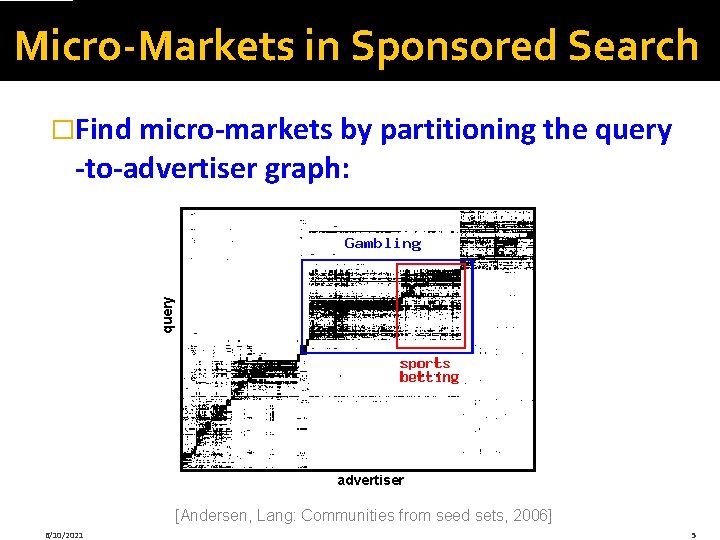
Micro-Markets in Sponsored Search �Find micro-markets by partitioning the query -to-advertiser graph: advertiser [Andersen, Lang: Communities from seed sets, 2006] 6/10/2021 5

Movies and Actors �Clusters in Movies-to-Actors graph: [Andersen, Lang: Communities from seed sets, 2006] 6/10/2021 6

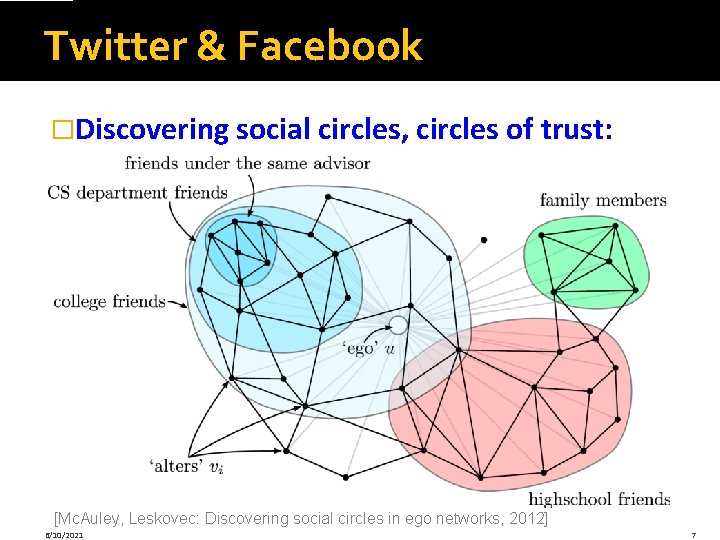
Twitter & Facebook �Discovering social circles, circles of trust: [Mc. Auley, Leskovec: Discovering social circles in ego networks, 2012] 6/10/2021 7

The Setting �Graph is large § Assume the graph fits in main memory § For example, to work with a 200 M node and 2 B edge graph one needs approx. 16 GB RAM § But the graph is too big for running anything more than linear time algorithms �We will cover a Page. Rank based algorithm for finding dense clusters § The runtime of the algorithm will be proportional to the cluster size (not the graph size!) 6/10/2021 8

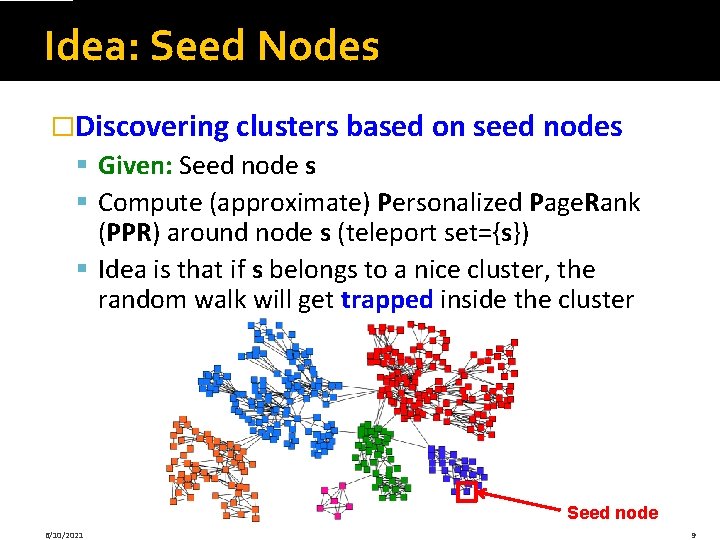
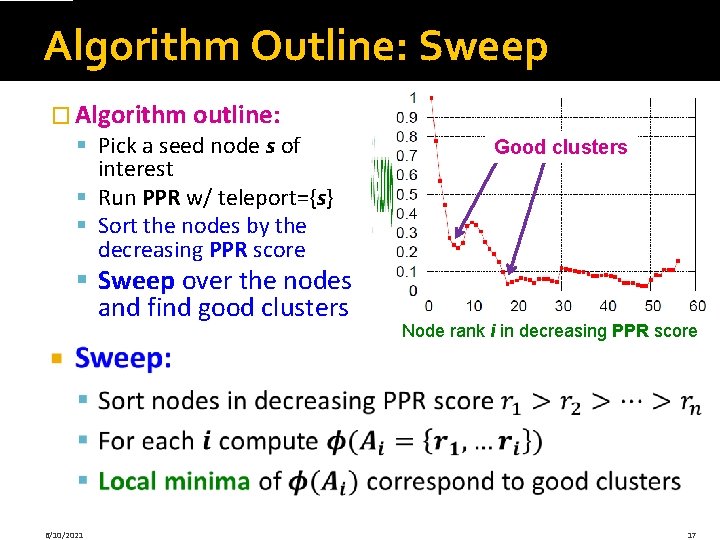
Idea: Seed Nodes �Discovering clusters based on seed nodes § Given: Seed node s § Compute (approximate) Personalized Page. Rank (PPR) around node s (teleport set={s}) § Idea is that if s belongs to a nice cluster, the random walk will get trapped inside the cluster Seed node 6/10/2021 9

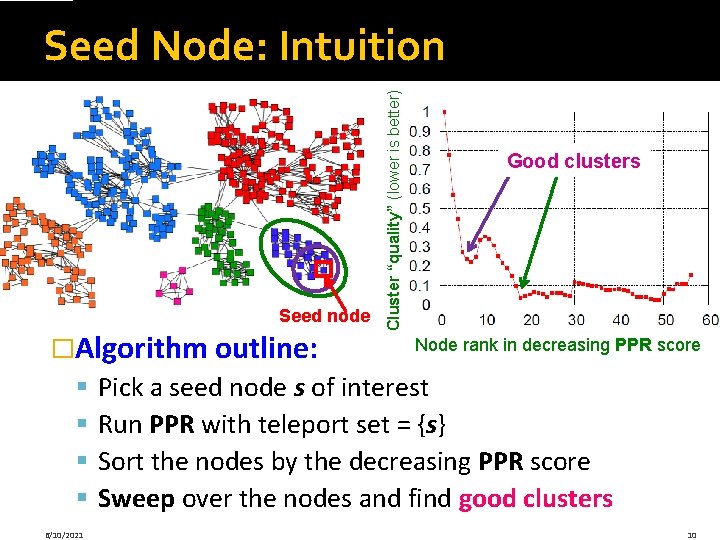
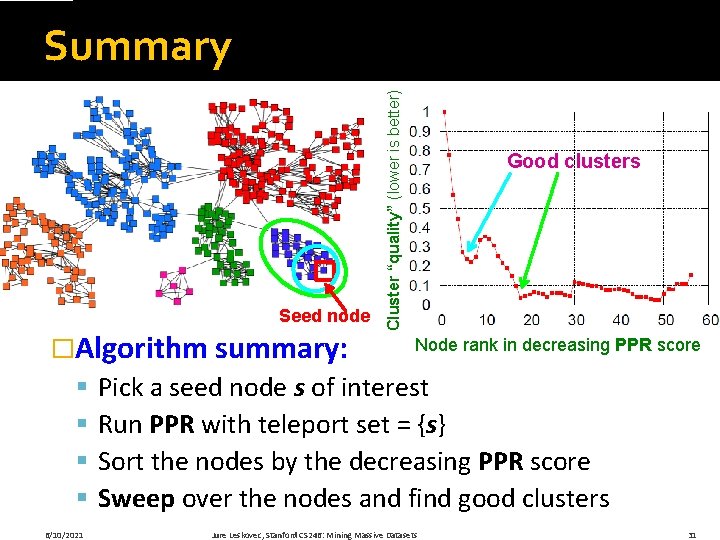
Seed node �Algorithm outline: § § 6/10/2021 Cluster “quality” (lower is better) Seed Node: Intuition Good clusters Node rank in decreasing PPR score Pick a seed node s of interest Run PPR with teleport set = {s} Sort the nodes by the decreasing PPR score Sweep over the nodes and find good clusters 10

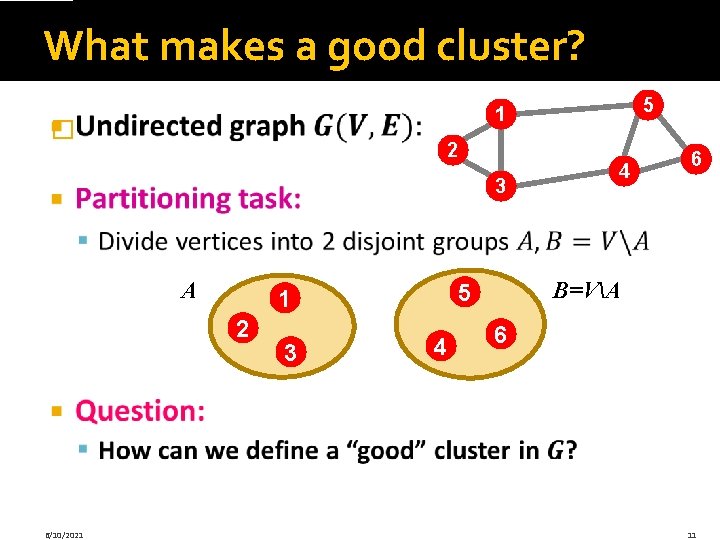
What makes a good cluster? � 2 3 A 3 4 4 6 B=VA 5 1 2 6/10/2021 5 1 6 11

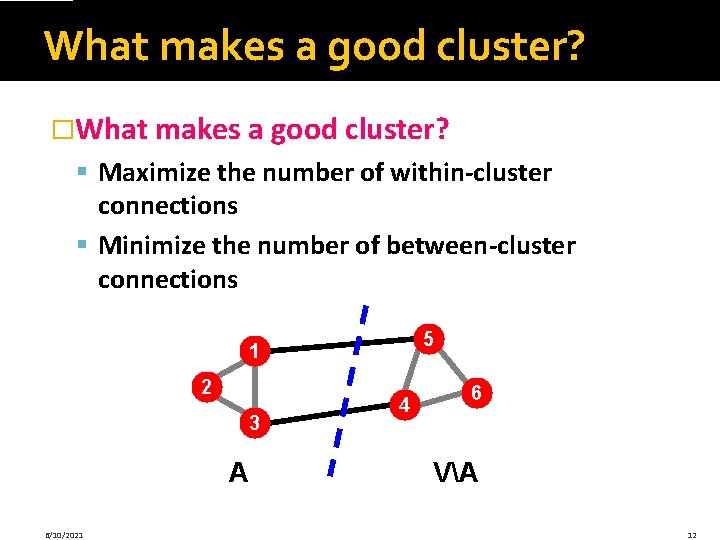
What makes a good cluster? �What makes a good cluster? § Maximize the number of within-cluster connections § Minimize the number of between-cluster connections 5 1 2 3 A 6/10/2021 4 6 VA 12

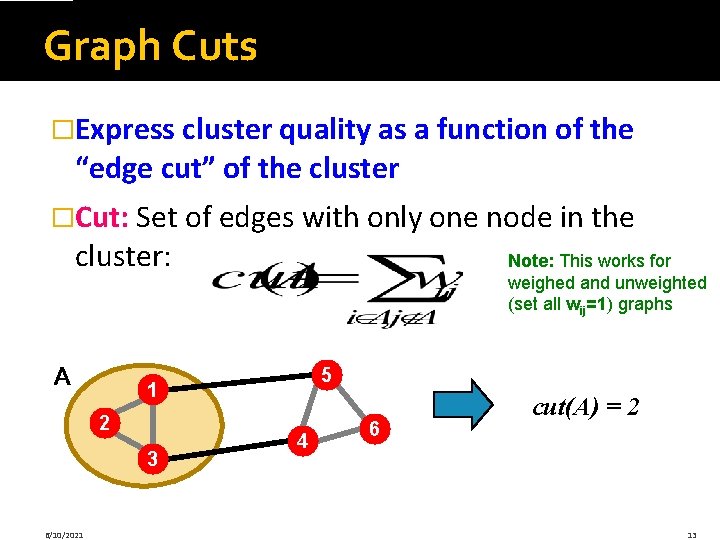
Graph Cuts �Express cluster quality as a function of the “edge cut” of the cluster �Cut: Set of edges with only one node in the cluster: A 5 1 2 3 6/10/2021 Note: This works for weighed and unweighted (set all wij=1) graphs 4 6 cut(A) = 2 13

Cut Score �Partition quality: Cut score § Quality of a cluster is the weight of connections pointing outside the cluster �Degenerate case: “Optimal cut” Minimum cut �Problem: § Only considers external cluster connections § Does not consider internal cluster connectivity 6/10/2021 14

Graph Partitioning Criteria [Shi-Malik] � m… number of edges of the graph di… degree of node i 6/10/2021 15

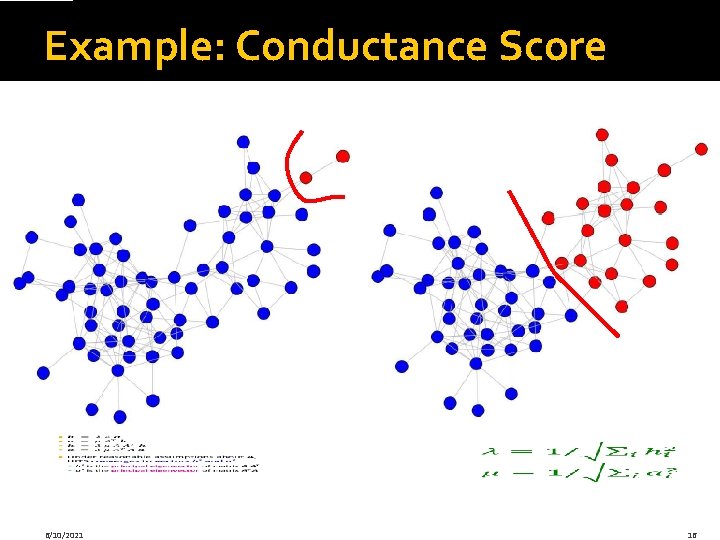
Example: Conductance Score 6/10/2021 16

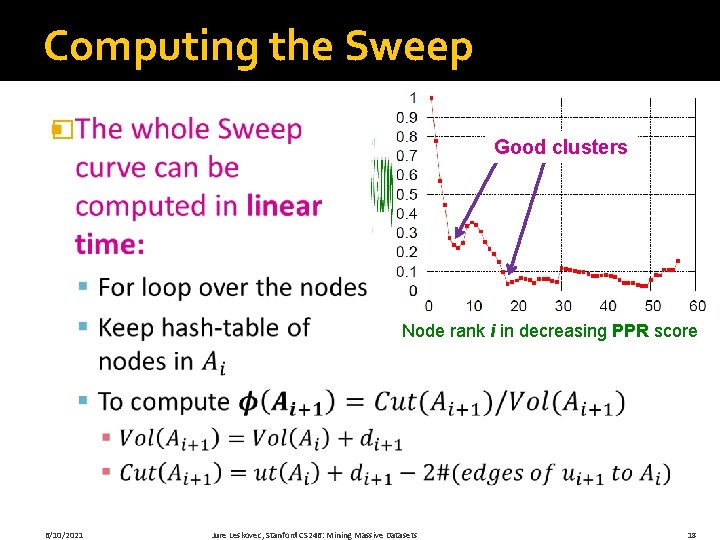
Algorithm Outline: Sweep � Algorithm outline: § Pick a seed node s of interest § Run PPR w/ teleport={s} § Sort the nodes by the decreasing PPR score § Sweep over the nodes and find good clusters 6/10/2021 Good clusters Node rank i in decreasing PPR score 17

Computing the Sweep � Good clusters Node rank i in decreasing PPR score 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 18

Computing PPR � At index S 6/10/2021 19

Approximate PPR: Overview � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 20

Towards approximate PPR � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 21

Towards approximate PPR � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 22

“Push” Operation � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets Update r Do 1 step of a walk: Stay at u with prob. ½ Spread remaining ½ fraction of qu as if a single step of random walk were applied to u 23

Intuition Behind Push Operation � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 24

Approximate PPR � At index S 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets r … PPR vector ru …PPR score of u q …residual PPR vector qu … residual of node u du … degree of u 25

Observations (1) � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 27

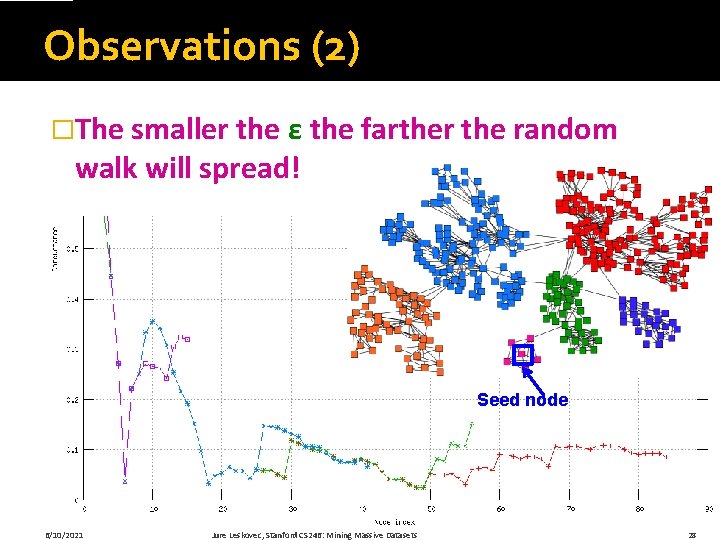
Observations (2) �The smaller the ε the farther the random walk will spread! Seed node 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 28

Observations (3) 6/10/2021 [Andersen, Lang: Communities from seed sets, 2006] Jure Leskovec, Stanford CS 246: Mining Massive Datasets 29

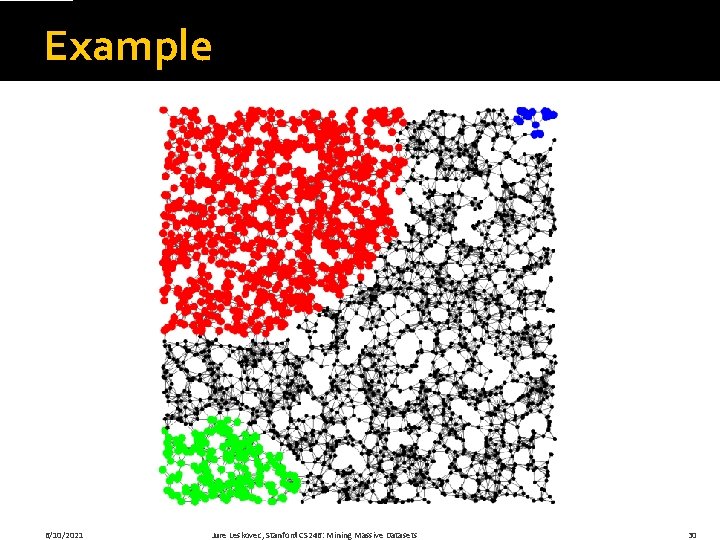
Example 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 30

Seed node �Algorithm summary: § § 6/10/2021 Cluster “quality” (lower is better) Summary Good clusters Node rank in decreasing PPR score Pick a seed node s of interest Run PPR with teleport set = {s} Sort the nodes by the decreasing PPR score Sweep over the nodes and find good clusters Jure Leskovec, Stanford CS 246: Mining Massive Datasets 31

Motif-Based Local Spectral Clustering Jure Leskovec, Stanford CS 246: Mining Massive Datasets

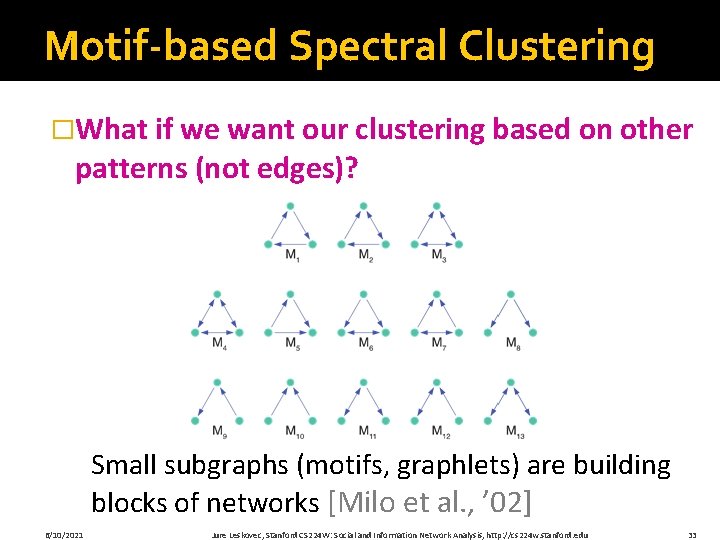
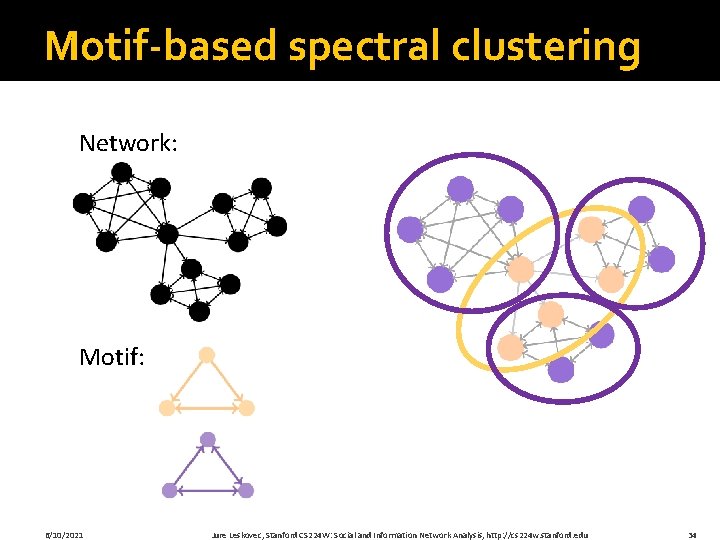
Motif-based Spectral Clustering �What if we want our clustering based on other patterns (not edges)? Small subgraphs (motifs, graphlets) are building blocks of networks [Milo et al. , ’ 02] 6/10/2021 Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 33

Motif-based spectral clustering Network: Motif: 6/10/2021 Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 34

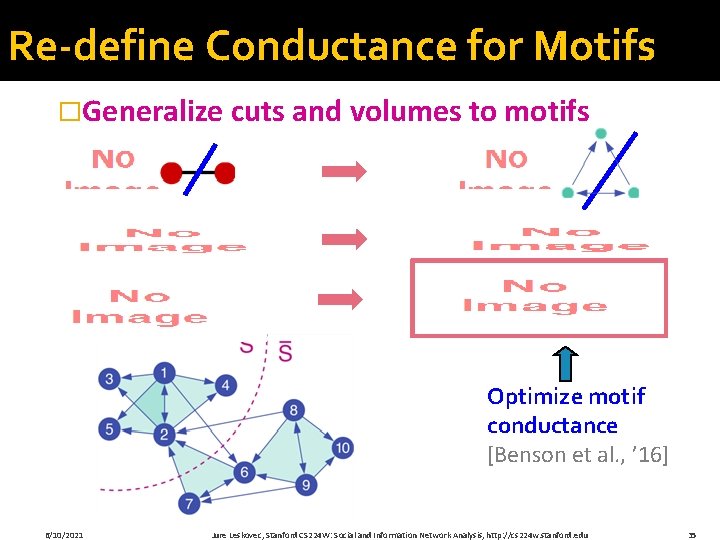
Re-define Conductance for Motifs �Generalize cuts and volumes to motifs Optimize motif conductance [Benson et al. , ’ 16] 6/10/2021 Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 35

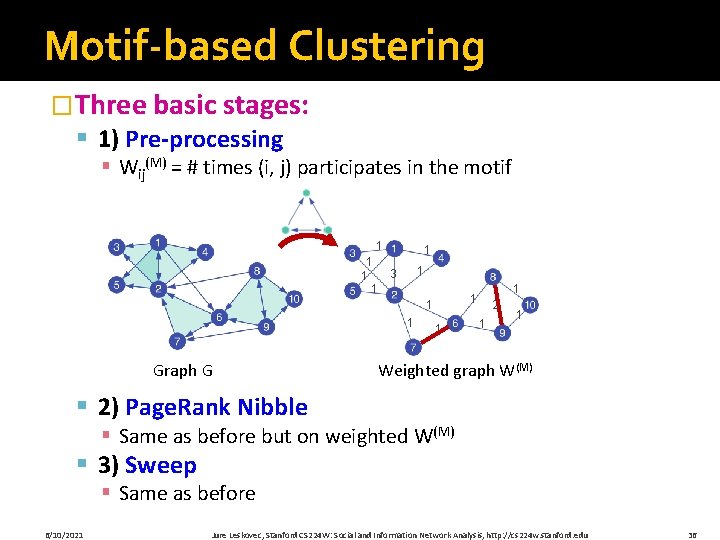
Motif-based Clustering �Three basic stages: § 1) Pre-processing § Wij(M) = # times (i, j) participates in the motif 1 1 1 3 1 1 1 Graph G 1 1 1 2 1 1 Weighted graph W(M) § 2) Page. Rank Nibble § Same as before but on weighted W(M) § 3) Sweep § Same as before 6/10/2021 Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 36

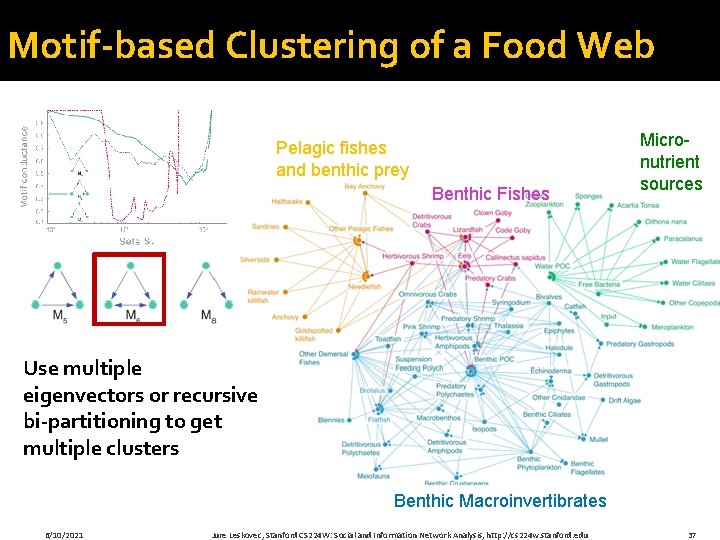
Motif-based Clustering of a Food Web Pelagic fishes and benthic prey Benthic Fishes Micronutrient sources Use multiple eigenvectors or recursive bi-partitioning to get multiple clusters Benthic Macroinvertibrates 6/10/2021 Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 37

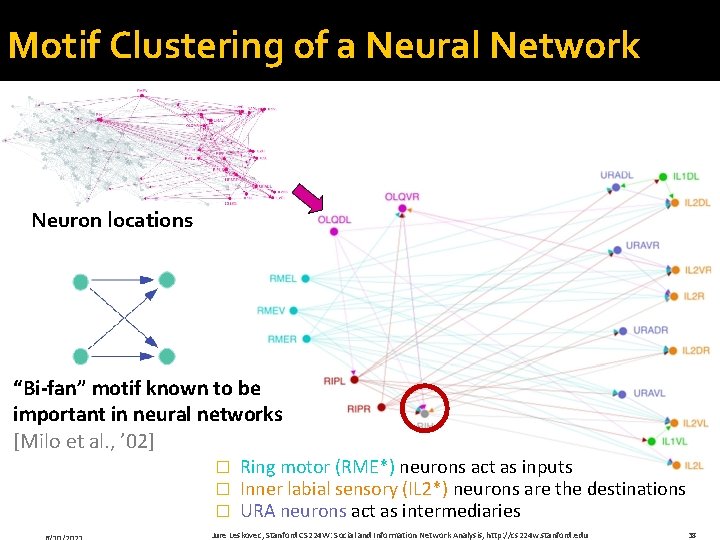
Motif Clustering of a Neural Network Neuron locations “Bi-fan” motif known to be important in neural networks [Milo et al. , ’ 02] � � � Ring motor (RME*) neurons act as inputs Inner labial sensory (IL 2*) neurons are the destinations URA neurons act as intermediaries Jure Leskovec, Stanford CS 224 W: Social and Information Network Analysis, http: //cs 224 w. stanford. edu 38

Analysis of Large Graphs: Trawling

[Kumar et al. ‘ 99] Method: Trawling �Search for small communities in a Web graph �What is the signature of a … … … community/discussion in a Web graph? Use this to define “topics”: What the same people on the left talk about on the right Remember HITS! Dense 2 -layer graph Intuition: Many people all talking about the same things 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 40

Searching for Small Communities � X K 3, 4 Y Fully connected 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 41

[Agrawal-Srikant ‘ 99] Remember: Frequent Itemsets � Products sold in a store 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 42

The Apriori Algorithm [Agrawal-Srikant ‘ 99] � 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 43

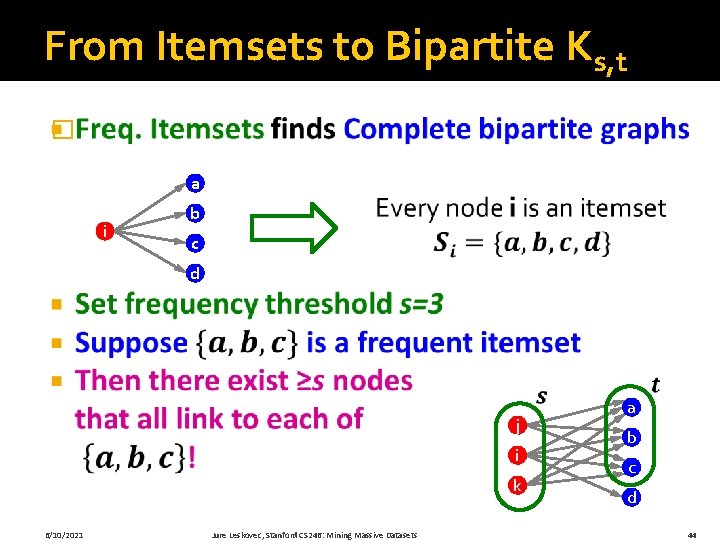
From Itemsets to Bipartite Ks, t � a i b c d j i k 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets a b c d 44

[Kumar et al. ‘ 99] From Itemsets to Bipartite Ks, t � a b i c d j i k X 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets a b c d Y 45

[Kumar et al. ‘ 99] From Itemsets to Bipartite Ks, t Say we find a frequent itemset Y={a, b, c} of supp s So, there are s nodes that link to all of {a, b, c}: View each node i as a set Si of nodes i points to a i b c d x Si={a, b, c, d} Find frequent itemsets: s … minimum support t … itemset size We found Ks, t! Ks, t = a set Y of size t that occurs in s sets Si 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets a a b b c y a z c b c x y X z a b c Y 46

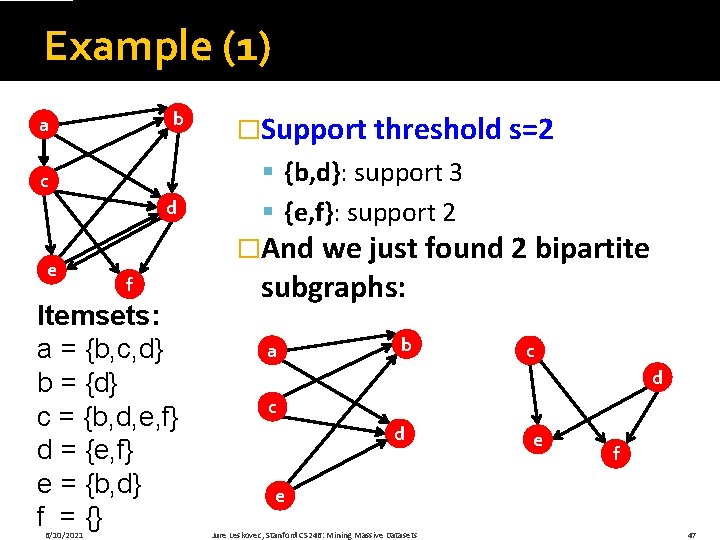
Example (1) b a c d e § {b, d}: support 3 § {e, f}: support 2 �And we just found 2 bipartite f Itemsets: a = {b, c, d} b = {d} c = {b, d, e, f} d = {e, f} e = {b, d} f = {} 6/10/2021 �Support threshold s=2 subgraphs: a b c d e f e Jure Leskovec, Stanford CS 246: Mining Massive Datasets 47

Example (2) �Example of a community from a web graph Nodes on the right Nodes on the left [Kumar, Raghavan, Rajagopalan, Tomkins: Trawling the Web for emerging cyber-communities 1999] 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets 48

[Kumar et al. ‘ 99] Trawling — Summary �Algorithmic result: § Frequent itemset extraction and dynamic programming find graphs Ks, t § Method is very scalable �Further improvements: Given s and t § (Repeatedly) prune out all nodes with out-degree < t and in-degree < s j i k 6/10/2021 Jure Leskovec, Stanford CS 246: Mining Massive Datasets a b c d 49