Communication Networks A Second Course Jean Walrand Department

Communication Networks A Second Course Jean Walrand Department of EECS University of California at Berkeley

Graph Theory • • Routing Coloring Qo. S in Ad Hoc Neworks Percolations Note: Some slides from Abhay Parekh, others from Rajarshi Gupta

Routing • Shortest Path: Principle of Optimality • Algorithms • Trees

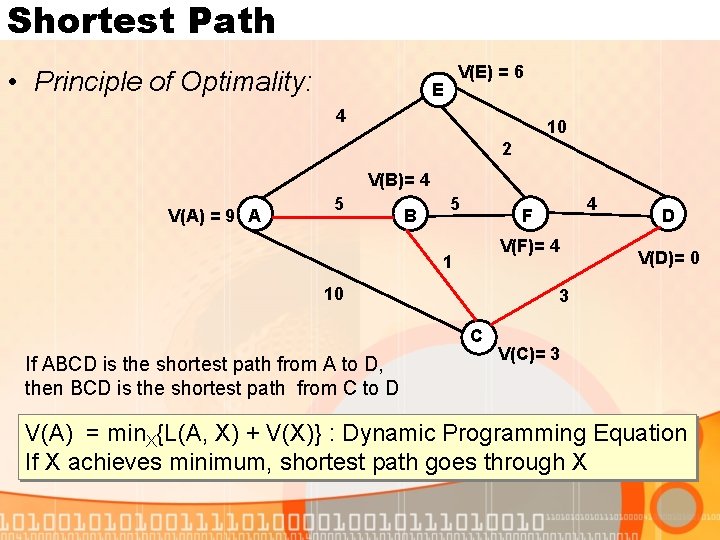
Shortest Path • Principle of Optimality: V(E) = 6 E 4 10 2 V(B)= 4 V(A) = 9 A 5 B 5 V(F)= 4 1 10 D V(D)= 0 3 C If ABCD is the shortest path from A to D, then BCD is the shortest path from C to D 4 F V(C)= 3 V(A) = min. X{L(A, X) + V(X)} : Dynamic Programming Equation If X achieves minimum, shortest path goes through X

Related Idea: Optimal Control • Problem: • Solution:

Related Idea: Optimal Control • Variation: • Solution:

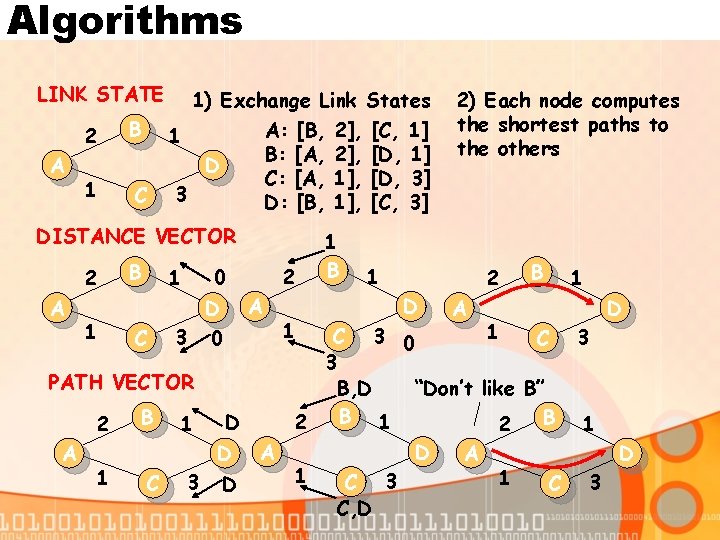
Algorithms LINK STATE A 2 B 1 C 1) Exchange Link States A: [B, 2], [C, 1] 1 B: [A, 2], [D, 1] D C: [A, 1], [D, 3] 3 D: [B, 1], [C, 3] DISTANCE VECTOR 2 A 1 B A D C 2 0 1 3 0 PATH VECTOR 2 A 1 B 1 D D C 3 D A 1 1 B 2) Each node computes the shortest paths to the others 1 2 D A B 1 D 1 C 3 0 C 3 3 B, D “Don’t like B” B 1 2 2 D A D 1 1 C 3 C, D

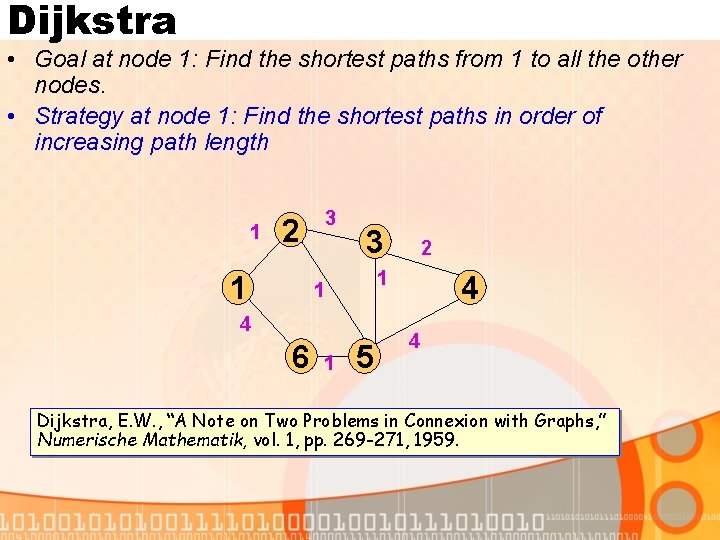
Dijkstra • Goal at node 1: Find the shortest paths from 1 to all the other nodes. • Strategy at node 1: Find the shortest paths in order of increasing path length 1 3 2 1 3 1 1 4 6 1 2 5 4 4 Dijkstra, E. W. , “A Note on Two Problems in Connexion with Graphs, ” Numerische Mathematik, vol. 1, pp. 269 -271, 1959.

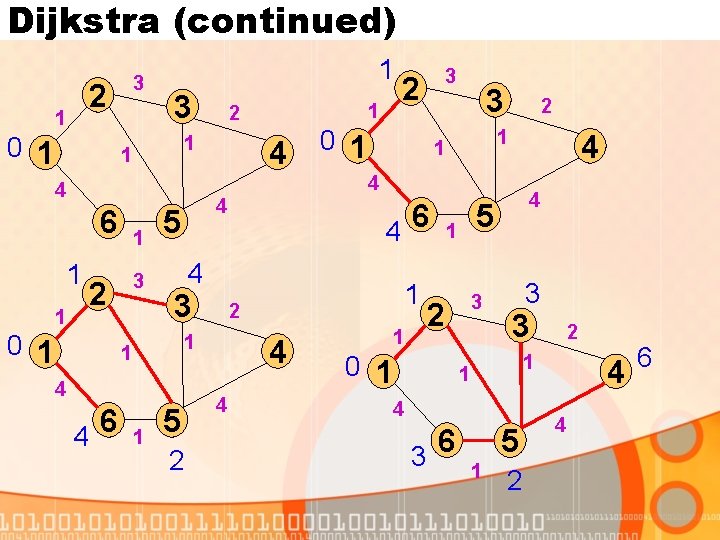
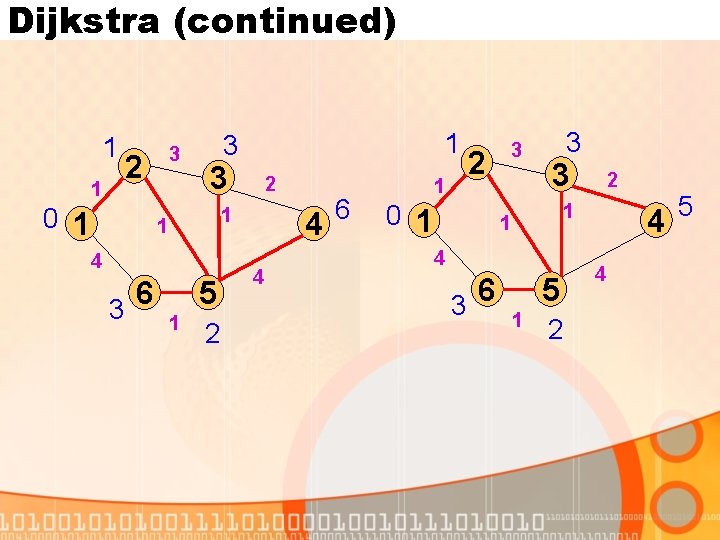
Dijkstra (continued) 3 2 1 0 1 1 3 1 1 4 2 0 1 3 2 1 1 4 4 4 6 1 1 1 2 3 1 3 2 0 1 4 5 4 3 4 1 5 2 1 1 6 4 4 4 1 5 1 3 2 0 1 4 3 3 1 1 4 3 2 6 5 1 2 4 4 6

Dijkstra (continued) 1 1 3 2 0 1 3 2 1 1 4 6 3 1 3 5 1 2 4 4 6 1 3 2 0 1 3 3 1 1 4 3 2 6 5 1 2 4 4 5

Dijkstra: Correctness • Thm: Label v(i) is the shortest path cost to i • Lemma: At one stage, algorithms labels nodes in a set P. It then adds nodes to P. Labels in P are the shortest path involving nodes in P. Then when P = V, theorem holds • Proof of Lemma • Suppose we have a shorter path using node in T • Let p, q in P be two nodes in path, with t in T in between • But if v(p) + d(p, t) + d(t, q) < v(p) + d(p, q), then we would have picked t before q (Contradiction)

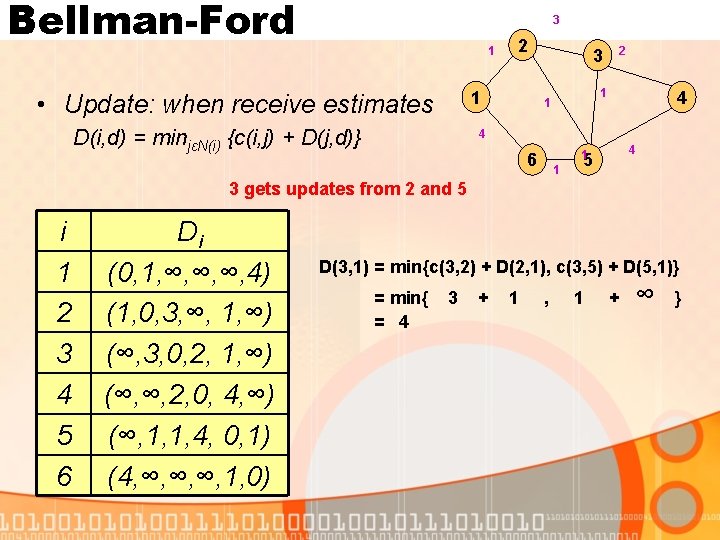
Bellman-Ford 3 1 2 1 • Update: when receive estimates D(i, d) = minjεN(i) {c(i, j) + D(j, d)} 3 2 1 1 4 4 4 1 6 1 5 3 gets updates from 2 and 5 i 1 2 3 4 5 6 Di (0, 1, ∞, ∞, ∞, 4) (1, 0, 3, ∞, 1, ∞) (∞, 3, 0, 2, 1, ∞) (∞, ∞, 2, 0, 4, ∞) (∞, 1, 1, 4, 0, 1) (4, ∞, ∞, ∞, 1, 0) D(3, 1) = min{c(3, 2) + D(2, 1), c(3, 5) + D(5, 1)} = min{ = 4 3 + 1 , 1 + ∞ }

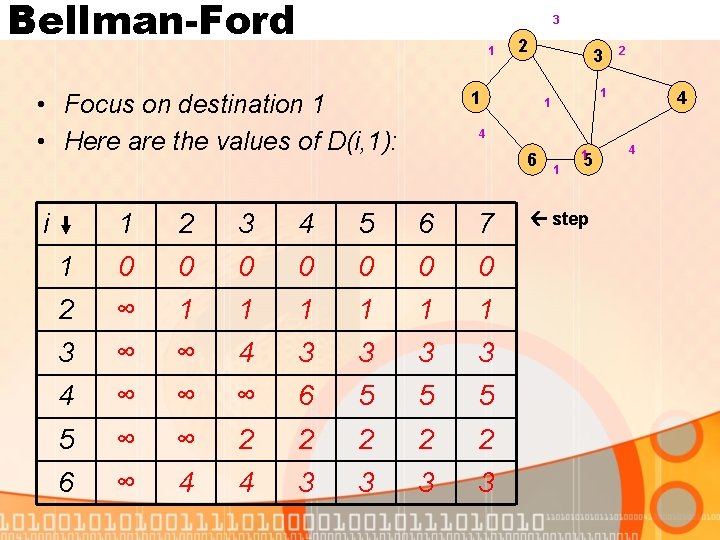
Bellman-Ford 3 1 • Focus on destination 1 • Here are the values of D(i, 1): i 2 2 1 1 4 4 6 1 2 3 4 5 6 7 1 0 0 0 0 2 ∞ 1 1 1 3 ∞ ∞ 4 3 3 4 ∞ ∞ ∞ 6 5 5 ∞ ∞ 2 2 2 6 ∞ 4 4 3 3 1 1 5 step 4

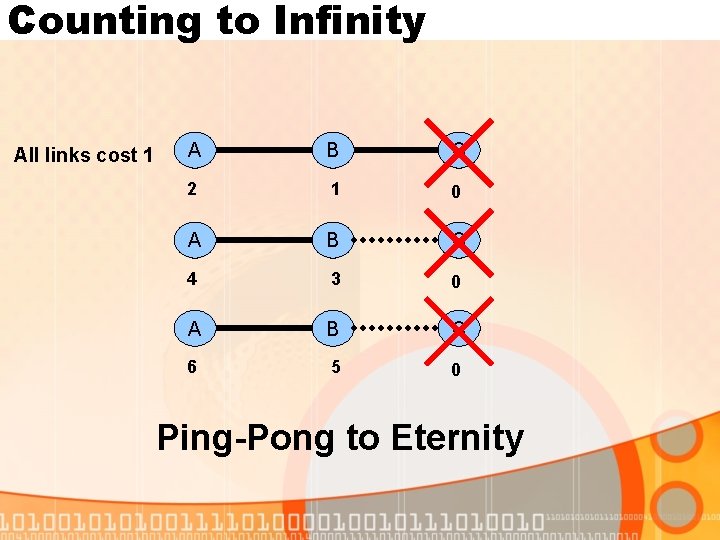
Counting to Infinity All links cost 1 A B C 2 1 0 A B C 4 3 0 A B C 6 5 0 Ping-Pong to Eternity

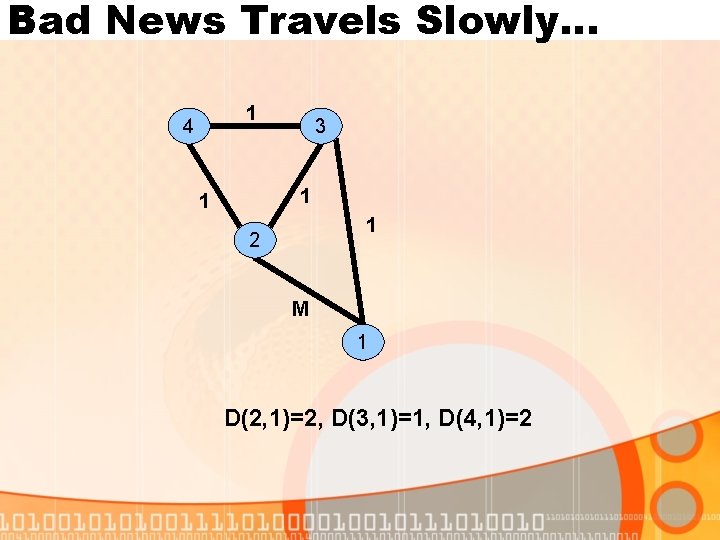
Bad News Travels Slowly… 1 4 3 1 1 1 2 M 1 D(2, 1)=2, D(3, 1)=1, D(4, 1)=2

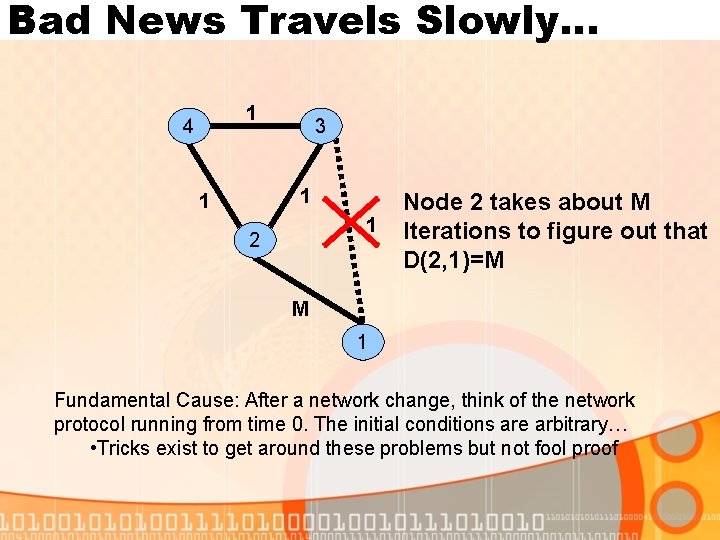
Bad News Travels Slowly… 1 4 3 1 1 1 2 Node 2 takes about M Iterations to figure out that D(2, 1)=M M 1 Fundamental Cause: After a network change, think of the network protocol running from time 0. The initial conditions are arbitrary… • Tricks exist to get around these problems but not fool proof

Asynchronous Bellman Ford • In general, nodes are using different and possibly inconsistent estimates • If no link changes after some time t, the algorithm will eventually converge to the shortest path • No synchronization required at all…

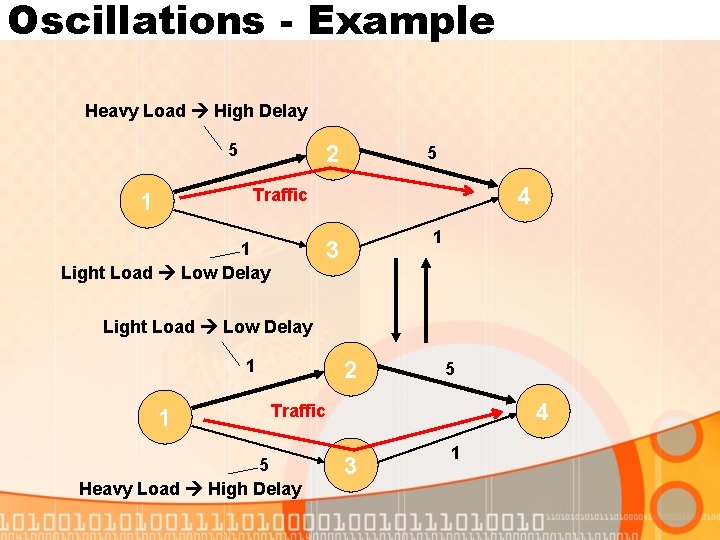
Oscillations • Link costs must reflect link speed AND congestion • Under both LSP and DV routing occurs over a tree • The costs of the links of this tree will increase • The other links will not be congested • Their costs will drop • Routing protocol will shift traffic and create a new tree • This process of shifting and reshifting can be severe • Way out: Change congestion costs slowly (exponential averaging) – Route dampening

Oscillations - Example Heavy Load High Delay 5 2 5 4 Traffic 1 1 3 1 Light Load Low Delay 1 1 2 5 4 Traffic 5 Heavy Load High Delay 3 1

Link State vs. Distance Vector No clear winner • LS is robust since it each node computes its own routes independently • Suffers from the weaknesses of the topology update protocol. Inconsistency etc. • Excellent choice for a well engineered network within one administrative domain • E. g. OSPF • DV works well when the network is large since it requires no synchronization and has a trivial topology update algorithm • • Suffers from convergence delays Very simple to implement at each node Excellent choice for large networks E. g. RIP

Trees Root

Useful Trees Types of Trees • Binary Tree • Each non-leaf node has exactly 2 children • Ternary Tree • Height Balanced Tree • Root chosen s. t. height is minimized • Bipartite Graphs Induced Trees • Formed by choosing a subset of V, E from G • Rooted Tree • Rooted at particular node • Spanning Tree • Covers every node • ‘Subset Spanning Tree’ • Covers every node in a chosen subset

Trees in Networks • Broadcast Tree • Search Trees • BFS • DFS • Spanning Tree Protocol (STP) in Bridged Networks (e. g. Ethernet) • Multicast Tree • And many, many other places …

Trees and Ethernet Tree Feature • Connected • No cycles • Removing any edge makes it disconnected • Adding any edge forms a cycle • Every pair of nodes has unique path • • • Ethernet Behavior Need all LANs to talk Loops cause broadcast storms Any bridge/port failure needs recomputation Need to disable all redundant ports Guarantees path with STP

Concrete Example • Weight balanced Spanning Tree (WBST) • Each edge has cost • e. g. 10/1000 Mbps • Choose spanning tree that has min difference between min and max edge cost • Want to minimize buffering requirements as packets move through the network. Also control jitter. • Complexity

Recall Spanning Tree Algos • Kruskal’s Greedy Algorithm to compute Spanning Tree • • 1. Order the edges in term of weight 2. Add lowest cost edge (provided no loops) 3. Check if all vertices are connected 4. If not, return to step 2 • Any search (BFS/DFS) can check for connectedness • BFS/DFS may be performed in O(m)

WBST : Algorithm • • Sort edges in increasing order of weight c 1<c 2<…<cm Initialize: diff = cm-c 1, low = 1, high = 1 Take Glow, high = G (V, {ci: low i high}) if Glow, high is connected • if diff > (chigh – clow) • diff : = chigh – clow • Remember low, high • low : = low + 1 • repeat • else • high : = high + 1 • repeat

WBST : Correctness • Spanning Tree exists • By checking Glow, high is connected => spanning tree must exist • Do this using DFS. Also finds the WBST • Why balanced • Keep adding low cost edges till graph connected • Then try to discard as many low cost edges • Move both ‘low’ and ‘high’ pointers to consider other ranges • Remember best diff

WBST : Complexity • In each iteration, we either increment low, or increment high • So max number of iterations = 2 m • Each iteration needs to check connectedness: DFS O(m) • So entire algo is O(m 2) • Think: How would we make this algorithm distributed

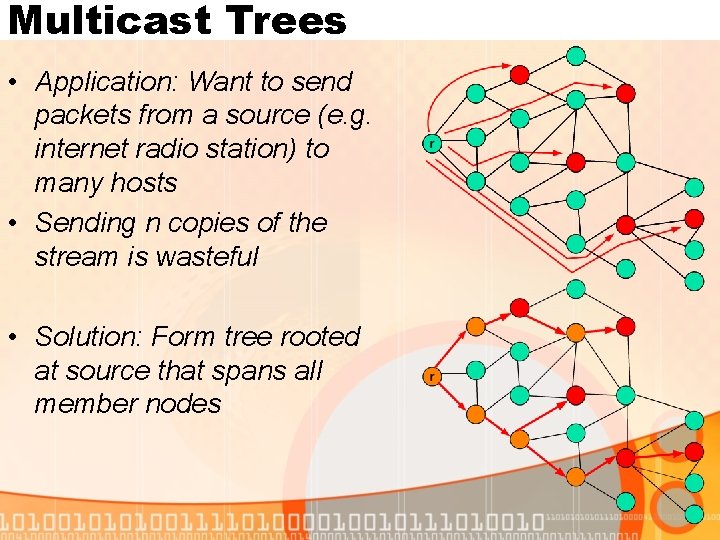
Multicast Trees • Application: Want to send packets from a source (e. g. internet radio station) to many hosts • Sending n copies of the stream is wasteful • Solution: Form tree rooted at source that spans all member nodes

Distributed Algorithm • Need to know address of group • First Join • • First member sends route request Request will be forwarded all the way to source Confirmation flows back to member All routers in path will add entry (mc_addr | port) • Subsequent Join • • New member send route request Request forwarded to router that has mc_addr entry Send confirmation from this point on Augment route entry (mc_addr | port 1, port 2) • Think: Optimal multicast tree

Multicast Algorithm (contd) • Leave/Pruning • Node leaving sends leave message to router • Router removes port from route entry • If last port entry deleted, send prune message to parent • Multi-source multicast tree • Less optimal: packets between two branches travel long distance • But need to minimize state in routers

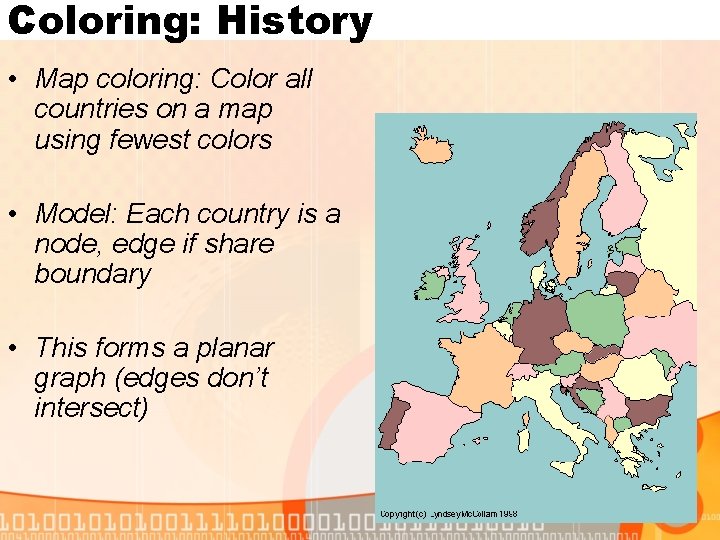
Coloring: History • Map coloring: Color all countries on a map using fewest colors • Model: Each country is a node, edge if share boundary • This forms a planar graph (edges don’t intersect)

4 & 5 Color Theorems • Five color theorem: Every planar graph is 5 colorable • Heawood, 1890 • Four Color Theorem: Every planar graph is 4 colorable • Conjectured for many years (since 1890) • Proved by Appel and Haken (1977) • Can do no better than 4 colors • K 4 (complete graph in 4 vertices) is planar

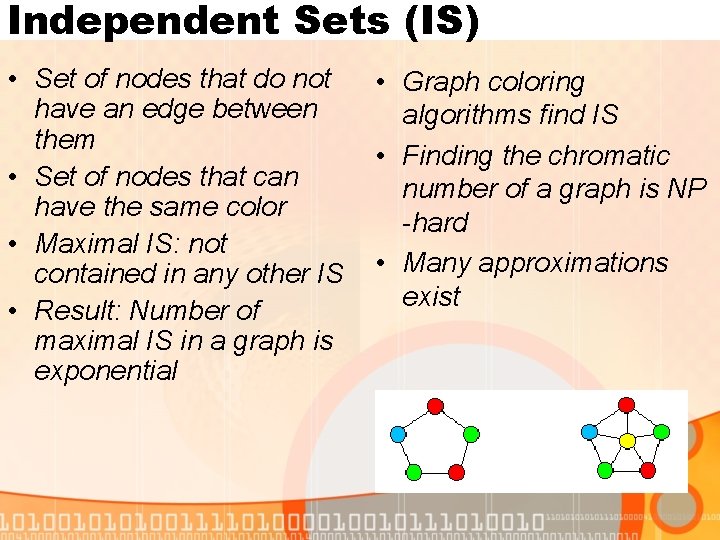
Independent Sets (IS) • Set of nodes that do not have an edge between them • Set of nodes that can have the same color • Maximal IS: not contained in any other IS • Result: Number of maximal IS in a graph is exponential • Graph coloring algorithms find IS • Finding the chromatic number of a graph is NP -hard • Many approximations exist

Approximate Coloring • Greedy Algorithm • Complexity • Order nodes by degree • Each iteration adds one • Add first node to IS node, so O(m) • Discard all neighbors into • Discarding neighbors O(n) a Future bin • Total: O(mn) • Repeat till set empty • Follow up: How far is this • Start with future bin from optimal coloring • Correctness • Are the sets generated independent ? • Are they maximal ? • Arbitrary or Bounded • Many approx algos give coloring within 4 X, 6 X of optimal

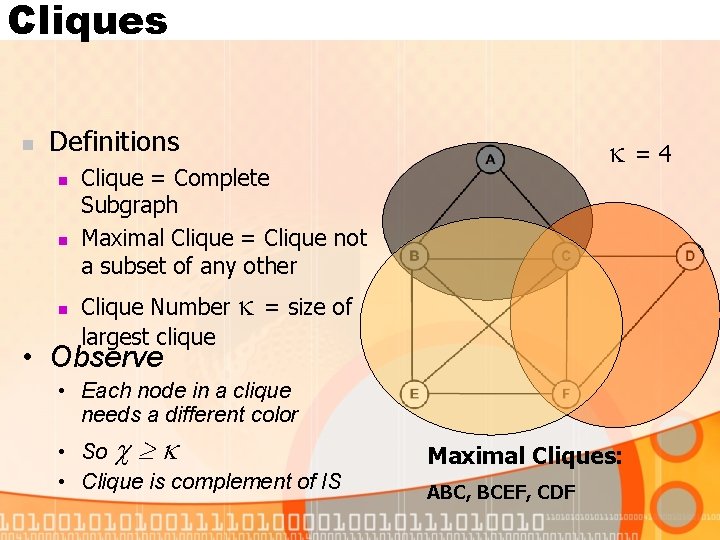
Cliques n Definitions n n n Clique = Complete Subgraph Maximal Clique = Clique not a subset of any other Clique Number largest clique = size of • Observe • Each node in a clique needs a different color • So • Clique is complement of IS Maximal Cliques: ABC, BCEF, CDF =4

Perfect Graphs • A graph is said to be perfect when its • Chromatic Number • Clique Number • Are equal • For all induced subgraphs • Strong Perfect Graph Theorem • Chudnovsky, Robertson, Seymour, Thomas (2002) • A graph is perfect if and only if it has no odd holes or odd antiholes • Odd-hole is a odd cycle with no chord • Odd anti-hole is complement of odd-hole