Communication data transfer 1 Selected parts of information

Communication, data transfer 1. Selected parts of information theory coding, transfer rates, enthropy, compression, encryption under continuous construction. . . 2018. 03. 25.

Units of information n n b, bit („binary digit”): basic unit of information in binary number system, with value of 0 or 1; can be used equivalently in digital technics as True (1) or False (0 or -1 or any other number if not in binary representation) B, byte: 1 B=8 b § also called „octet” (eg. in French), partly because byte is not trivially 8 b (historically other formats existed) n Modern computers, processors and controllers are typically based on n*8 b representation of data (eg. memory cell size, ALU size or data bus size etc. )

Binary prefixes n n n Binary storage devices typically have sizes that are powers of two (question: why? ) Thus was the K=1024 prefix developed long ago They agreed that k=1000 and K=1024, but it was not universal of course Larger prefixes (M, G, T) are already capital letters so problems arose Especially with hard disks (1 TB=? B)

Binary prefixes 1999: IEC 60027 -2 Amendment 2 n to make prefixes unambigous n traditional SI prefixes are decimal n new binary prefixes: n Ki, Mi, Gi, Ti etc. n Ki. B: kibibyte, Mi. B: mebibyet etc. n („kilo binary byte”)

ASCII n n n American Standard Code for Information Interchange Original version: 1963, actual: 1986 7 bit symbols, 128 characters: lowercase and uppercase letters, numbers, special characters, control characters ¨ control chars: eg. new line, carriage return, tabulator, end-of-file etc. – some were made for printers ¨ n Numbers’ format: 011 0000 to 011 1001 (notice the code contains the number) n A: 100 0001, a: 110 0001 (A+32) n Originally the 8. bit was used as parity Later it was extended. Using the 8. bit another 128 characters were added, but these are not standard. More than 200 „code pages” exist. n

Units of information transfer Bit rate: number of bits transferred in unit time [b/s] n informal unit notations: n ¨ bps (bit per second) ¨ Bps (byte per second) n CASE SENSITIVE! 1 Bps=8 bps

Units of information transfer n Gross bit rate (raw bit rate, data signaling rate): ¨ Counts n all ("physical") bits Net bit rate (information rate): ¨ counts only bits containing the message (information), discounts bits for header, error correction, etc. ¨ net bit rate <= gross bit rate ¨ eg. 4 B 5 B coding (4 bit over 5 bit) (Ethernet): n 100 Mb/s net, 125 Mb/s gross bit rate

Units of information transfer n Symbol rate: ¨ symbols transferred per unit time ¨ unit: baud (Bd) = symbol per second n n only in binary coding!: 1 baud=1 b/s non binary: ¨ one symbol can be decoded to binary with more than one bits ¨ used eg. in modulations such as QAM, QPSK

Units of information transfer

Channel capacity (C) the upper limit of the gross bit rate of a noisy channel, while keeping an arbitrarily small bit error rate (without using error correction codes) n in principle, a noiseless channel could have infinite bit rate, but as noise increases, the useful bit rate decreases n see: Shannon-Hartley (later) n

Bandwidth n More meanings in vernacular: ¨ actual transfer rate of information (bitrate R) ¨ channel capacity C (maximum of R) ¨ spectral bandwidth (B) (we'll use this) n the bandwidth of the frequency spectrum of the signal transmitted ¨ can be -3 d. B bandwidth, but also can be measured btw zero points. . These are related, but not the same! n Eg. for same bit rate, B will be dependent on coding/modulation n

Bandwidth

Bandwidth n Eg. binary baseband signal ¨ N=1; n max 2 (b/s) / Hz 7 For double side band (DSB) modulations, only half of bandwidth counts ¨ eg. 16 QAM: N=4; max 4 (b/s) / Hz

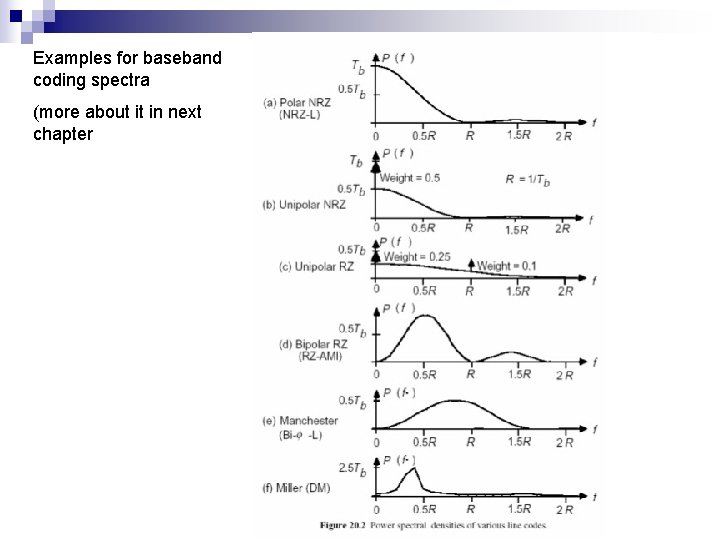
Examples for baseband coding spectra (more about it in next chapter

Noise, interference, error n noise ¨ often: n additive white gaussian noise (AWGN) interference ¨ EMI (electromagnetic int. ) ¨ crosstalk (between wires/signals) ¨ ISI (inter-symbol int. ) n n n distortion SNR: Signal to Noise Ratio SINR: Signal to Noise and Interference Ratio

Distortion n "linear distortion" ¨ doesn't introduce new frequency (spectral) components ¨ modifies existing spectral components n n (of course the relation of input and output signal is still nonlinear, but it can be achieved by linear circuits, eg. filters) "nonlinear distortion": ¨ introduces new spectral components ¨ made by circuits with nonlinear characteristics ¨ eg. diode/transistor, limiting circuit

Bit Error Ratio (BER) n Bit Error Probability (theoretical probability of a bit error) ¨ BER n is converging to BEP (see prob. calculus) BER used in practice is max 50% ¨ for a totally random channel ¨ question: why?

Bit Error Ratio (BER) n BER is made worse by: ¨ noise, n interference, distortion Modify by (possibly): ¨ amplitude, bit time, baseband coding, modulation ¨ error correcting codes

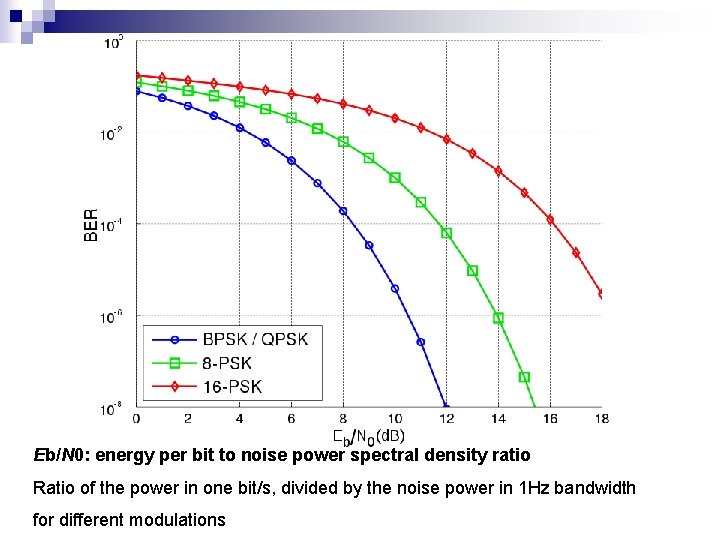
Eb/N 0: energy per bit to noise power spectral density ratio Ratio of the power in one bit/s, divided by the noise power in 1 Hz bandwidth for different modulations

Number of symbols n Number of symbols available (in "alphabet"): M (which is often a power of two, ie. M=2^N) ¨ n remember: one symbol is transmitted in a "unit time" If M (N) is increased: ¨ spectral n efficiency (R/B) is increased, ie. a larger bit rate can be achieved on the same spectral bandwidth ¨ the distance between levels (be it amplitude or frequency or phase) will be smaller, thus it will be more sensitive to noise n see the BER graph: if M is smaller, a lower Eb/N 0 is needed to achieve the same BER

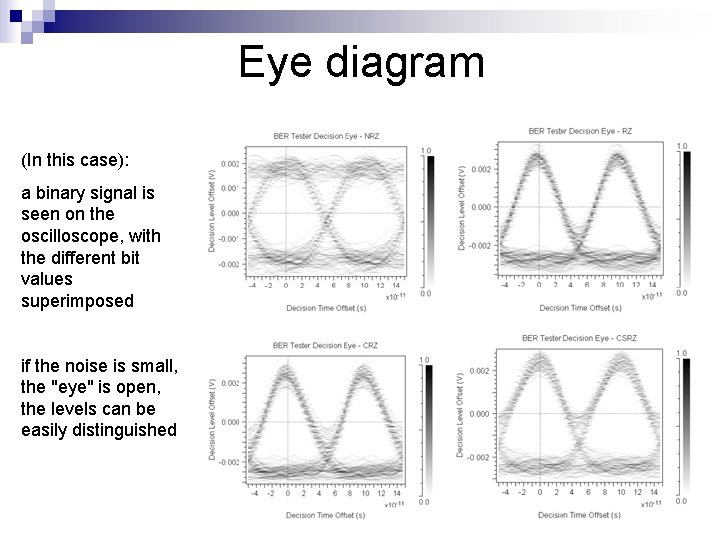
Eye diagram (In this case): a binary signal is seen on the oscilloscope, with the different bit values superimposed if the noise is small, the "eye" is open, the levels can be easily distinguished

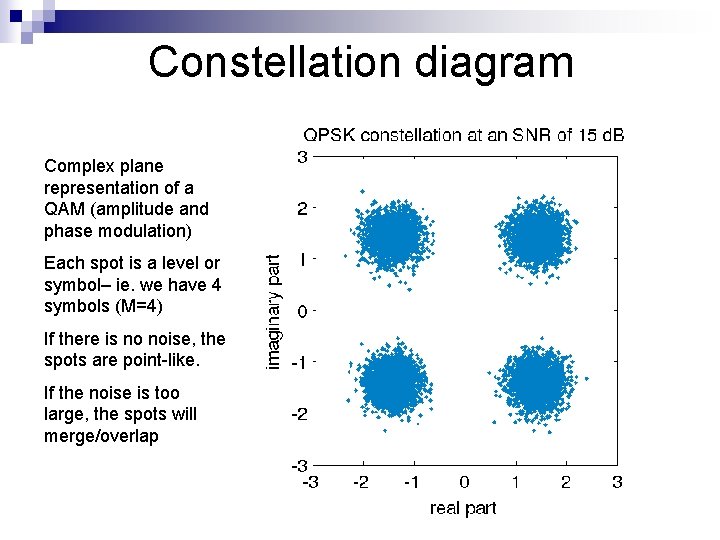
Constellation diagram Complex plane representation of a QAM (amplitude and phase modulation) Each spot is a level or symbol– ie. we have 4 symbols (M=4) If there is no noise, the spots are point-like. If the noise is too large, the spots will merge/overlap

Shannon-Hartley theorem n Relationship between channel capacity, bandwidth and signal-to-noise ratio

Shannon-Hartley theorem n If no noise: S/N is infinite => capacity is infinite even if bandwidth is finite ¨ remember: if B constant, bit rate can be increased by using larger M (alphabet) n If noise increased: capacity decreased ¨ as in earlier, we mean that the bit error rate is to be kept arbitrarily low

Shannon-Hartley theorem In noisy channel: Combined with Hartley's theorem, we can get an estimation on the max number of levels (symbol) usable (ideally):

Entropy according to Shannon: X: stochastic variable with possible outcomes {x 1. . . xn}, with probability distribution P(X) with values P(xi). Here the xi are the codewords (symbols) with P(xi) probability of occuring in the message. Entropy is practically about the information content of a message. If all symbols have the same probability, then entropy is maximal.

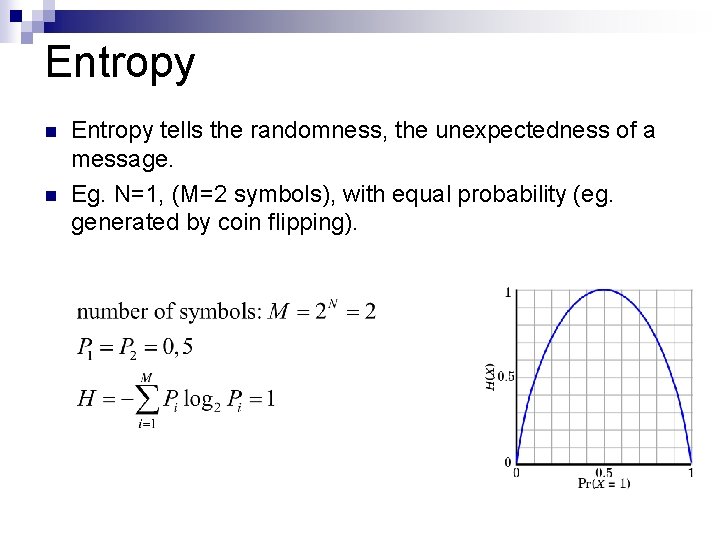
Entropy n n Entropy tells the randomness, the unexpectedness of a message. Eg. N=1, (M=2 symbols), with equal probability (eg. generated by coin flipping).

Entropy Eg. N=2, (M=4 symbols), equal probability. Entropy is 2 shannon (bit). This is correlating with the fact that in an alphabet of 4 symbols, each symbol can be converted to a 2 bit binary representation. In a binary code with equal prob. , the entropy is 1 (see prev. page). With equal probabilities: H=N

Entropy Eg. N=2, (M=4 symbols), not equal probability (one symbol more probable than the others). The entropy is 1, 36 shannon (bit), which is smaller than the previous case. This can interpreted as saying, that if symbol x 1 arrives, it is the most "expected", thus conveys less information than the others. For example if one symbol has probability=1 (certain outcome) then thus the others have to be 0, then entropy is 0, because we are certain that we'll always receive the one symbol with P=1, thus no news is gained.

Question? Randomness as a measure of information can be problematic in practice n Eg. how random is the following series? How much can it be compressed? n 11. 00100100001111110110100010000101101000110000110100110 0010011000101000101110000 000110111000001110011010001 n

Lossless compression n n If entropy is smaller than N, there is a possibility of lossless compression. The new code created can not have an average code word length longer than the entropy of the message. (Shannon's source coding theorem, 1948) There exists no such compression algorithm, that would work on all messages (ie. make them smaller) a simple proof: try compressing an already compressed message ¨ There are different methods used for different message types, eg. text, image, executable files, video, music etc. ¨

Lossless compression using binary representation of codes: n variable length code: we associate target symbols (codewords) of different length (number of bits) to each source symbol n prefix-free: no codeword starts with another codeword n ¨ eg. {0; 01; 10} set is not prefix-free, because 01 starts with 0 ¨ but {0; 110; 111} is prefix-free

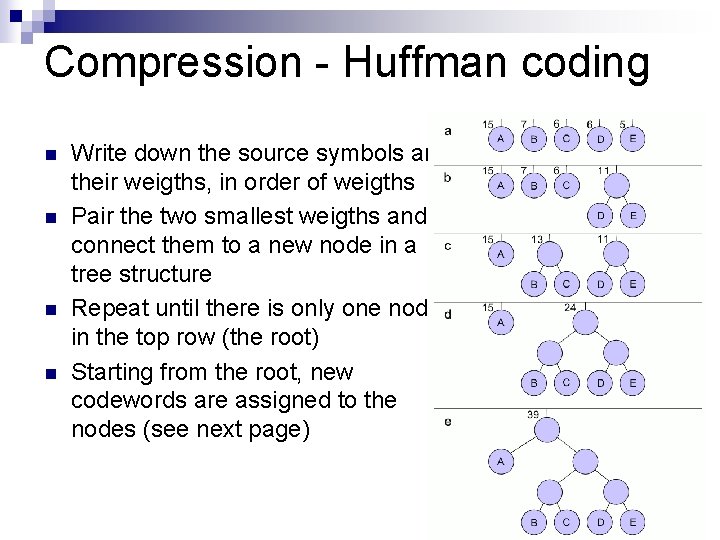
Compression - Huffman coding n n n prefix-free, variable length code it has the minimal average code word length given: the source symbols with their probability (or relative frequency of occurance) (this is also called weight here)

Compression - Huffman coding n n Write down the source symbols and their weigths, in order of weigths Pair the two smallest weigths and connect them to a new node in a tree structure Repeat until there is only one node in the top row (the root) Starting from the root, new codewords are assigned to the nodes (see next page)

Compression - Huffman coding

Question For example we have a binary code with: n P(0)=0, 9 n P(1)=0, 1 n Entropy is 0, 47 so we feel we could achieve good compression n Huffman coding, as shown previously, can not be directly applied n What to do? n

Compression n LZ algorithm

Sound/voice coding n base: ¨ PCM, n ADPCM lossless: ¨ FLAC, n MLP lossy: ¨ MPEG ¨ GSM Layer III (MP 3)

Voice coding n FLAC: Free Lossless Audio Codec § Linear predictor based The next sample is approximated as a linear function of previous samples Transmits the coefficients of the linear functions and the error (difference of approx. and real sample) Compression ratio of 40 -50% § § §

Voice coding Lossy compression: n utilizes the knowledge about human hearing (psychoacoustics) n eg. a louder sound can "mask" another one n eg. two slightly different frequencies can not always be perceived to be separate n also the stereo channels are often very similar, allowing to encode the difference only for one channel n

Redundancy n n n Eg. human languages are redundant ¨ Hwo stnarge we cna raed tihs. ¨ Evn tis txt cn b undrstod, if hrdly. Redundancy also means possibility of compression. If we keep redundancy, it gives: ¨ some protection against noise, interference / the ability to correct errors

Error detection and correction n Error detecting codes ¨ message n n has to be sent again need a two-way channel! Error correcting codes (ECC) ¨ message doesn't have to be sent again ¨ Forward Error Correction (FEC): called forward, because no talk-back (re-send) is needed

Error detection and correction n Generally, methods for detecting or correcting errors will increase the total amount of data transmitted for the same amount of actual information. That is, the gross bit rate is greater than the net bit rate.

Error detection: parity n n n Simplest error detection method: parity bit (for binary codes) Plus one bit at the end of the message (or frame, usually a byte) will make the total number of ones either odd or even. We can detect the error (in binary: inversion) of an odd number of bits. Can not correct, the message/frame/byte has to be resent. Eg. ASCII was originally 7 b code and 8. bit was the parity. Other apps: SCSI, PCI, cache, UART, etc.

Error correction: repetition code n Send each bit (or message/frame) n times. If not all received are the same, make a majority decision (it helps if n is odd). Net bit rate is 1/n times the gross bit rate. Eg. 5 b version: Flex. Ray automobile bus system. Also used in space probes. n Similar method for hardware: Triple Modular Redundancy, TMR n n storages (eg. some ECC RAM) – total storage capacity changes ¨ on board computer and other hw multiplied (eg. spacecraft) ¨ homework: create a majority logic gate (it creates the majority decision) ¨

Error correction: Hamming code For every n bit of message, create an m+n bit long code word n eg. (7, 4) code: for every 4 bits, add +3 bits n detects 1 or 2 bits of error n or corrects 1 bit of error n used eg. in ECC RAM n

Error correction – burst error n Burst error: if a larger group of neighbouring bits are involved ¨ esp. in radio or optical comms. ¨ Most methods can only correct a few bits of error in a larger frame. n =>interleaving: the message is broken into smaller parts, which are re-ordered before transmission. After reception, order is restored, thus groups errors are broken into more but smaller error groups.

Encryption Coding can be thought of as a one-to-one relation btw two sets of symbols n If someone doesn’t know the second set of symbols or the relationship, then it is also encryption. n

Encryption terms Encryption: the act of making a message secret n Cryptography: the science of encryption n Plaintext: the source message, not encrypted n Cleartext: info stored/sent without encryption n Ciphertext: encrypted message n

Encryption n Possible methods ¨ Encrypting n the contents of the message this will presented first ¨ Hiding the message or the act of communication

Encryption n In practice, we have to keep in mind that most methods can be decyphered if given enough time. We have to choose a method such that the decyphering time is longer than the actuality of the message, or the cost of decyphering is larger than it is worth. For electronic communication, usage of special characters, symbols is not applicable, so we use methods that relate eg. latin characters to latin characters, or more correctly, binary numbers to binary numbers.

Encryption Suppose encrypting human text. n Simple relation of latin-to-latin characters: n ¨ shift all characters by same number: A->C; B->D; Z->B, etc n almost trivial to decypher ¨ relate n randomly just a little bit harder

Encryption n Decyphering simple codes: ¨ Find out the language (eg. from knowing the sender and receiver, or trying – it’s a finite set) ¨ Need a table of character relative frequency of that language ¨ Need a dictionary of that language ¨ Often start with 1. . 2 letter words.

Encryption n Make the previous methods a little bit more complicated: ¨ code the „space” character also into something else ¨ use multi-language text, make some spelling errors

Encryption If we use the same method for a longer time (for many messages), or use longer messages, the chance of decyphering will be close to 1. n Therefore we need a method where the encryption process is split into two: a fix algorithm and a changing part (the cryptographic key) n

Encryption Security through obscurity: when we trust the algorithm to be unknown – don’t! n With keyed techniques, the knowledge of the algorithm without the key is not enough to decypher. n

Encryption To defeat frequency analysis: n Instead of 1 -to-1 relation, each letter (symbol) in the source will be related to another based on its position in the text. n Thus the same letter can be coded to different letters each time. n This relation is accomplished using the key, which can be a series of letters or numbers. n

Encryption n Example: Write the message in a row, under it the key, then use some algorithm on letters (or numbers) in one column to form a third one, write these in the third row to create the cyphertext. If the key is shorter than the message, copy it enough times after itself. This of course weakens the method.

Encryption Example: n Source: „ez a szoveg titkositando” n Key: „a kulcsmondat” n Method: sum of letters modulo 27 (space=1, a=2, b=3, etc) n Result: „g lwmwsbktlbnkuwjemmocst” n

Encryption n n One time pad (OTP): key used only onces G. S. Vernam : XOR method one time pad, 1919. ¨ check: XOR can be used both ways (to encrypt and decrypt) n OTP can be theoretically unbreakable if: ¨ key is really only used once (for one message) ¨ key is at least as long as the message ¨ key is random n Please note that purely with software you can’t create true random series ¨ you need some hw source (eg. thermal noise, tunnel effect, radioactive decay)

Part of a key book from Germany WWII, using Enigma

Encryption n Decyphering OTP ¨ code book is acquired ¨ keys are re-used ¨ key is not random ¨ see: Venona project, Lorenz, Enigma

Public key cryptography A big problem with OTP is the sending of the pair of the code book to the recipient. Especially hard if you want to send message to someone you didn’t meet before. n To solve this, Public-Key Cryptography was invented. n

Public key cryptography Everyone has two keys: a public and a private. n Aims: n ¨ to identify the sender (digital signature) ¨ to check if message was tampered with ¨ to encrypt message n these two can be done alone or together ¨ solve n problem of sending keys public key can be sent on unencrypted channel

Public key cryptography n Method of sending message: ¨ Use receiver’s public key to encrypt message. ¨ Receiver can decrypt it using her private key. ¨ This is called asymmetric encryption (different key need to encrypt and decrypt) ¨ hybrid cryptosystems: in practice often a traditional symmetric key is encrypted using the above method and rest of message is traditional (because asymm. encryption needs more calc. resources) n Keep your private key secret. Public key is found in „phone books”.

Public key cryptography n To check identity of sender or whether message was altered by third party: ¨ sender creates a „hash” (a short block made from the message using special algorithm), which is appended to the end of the message (encrypted of course) ¨ receiver also calculates hash and compares it to the sender’s (decrypted using the sender’s public key)

Public key cryptography Problem: n Identity: we can only know that it was sent by someone with a given public key; but we can’t be sure of her real identity n solution trials: n ¨ public-key infrastructure (PKI), web of trust (decentralization)

Public key cryptography Mathematical foundation (most usual): calculation of prime factors n It is very easy (quick) to multiply two very large prime numbers. n It is very hard (very slow) to find the prime factors from the result. n Ie. it is an asymmetric algorithm n

Public key cryptography n n n Calculation resources needed Let „n” be the „size” of the input. (Think about the number of cities in the travelling salesman problem. ) If the algorithm to solve the problem needs running time proportional to a polinomial function of n then this problem is member of P class of problems. It is supposed that there exists a class of problems that can only be solved much slower (eg. exponential – polinomial is very slow, but exp is much slower). If n is large, these problems can take millions of years with the best computers. This class is the NP class. Such a problem is prime factorization. (Interesting fact: if one NP full problem is solved in P time, then all can be solved. ) If a faster way of solving NP problems is found, the world’s cryptography (think banking, military, company data etc) would crumble? Quantum computers might give a solution. . .

Public key cryptography a method : RSA n m: message; n, e: public key of receiver, d: private key of receiver; c: encrypted message n coding: n decoding: n

Encryption n Other methods ¨ using code words ¨ hiding of message steganography n communication below noise level (spread spectrum) n ¨ misguiding – hide the true message by sending a more visible false message

Encryption code words – these have previously agreed meaning ¨ ie. Navajo codespeakers in WWII: language is known by only few people, and used codewords (ie. names of animals for ships etc) ¨ hard to decode if sparingly used, esp. if more codewords have similar meaning ¨ Often the codewords are put into a sentence, the rest of the sentence having no real meaning, just for misguiding.