COMBUSTION of PROPANE 1 What does the reaction

COMBUSTION of PROPANE 1. What does the reaction involve? (reactants and products) Reaction needs to be balanced

COMBUSTION of PROPANE 2. Envision the “structural formulas” for the reactants and the products (from your knowledge of Lewis structures)

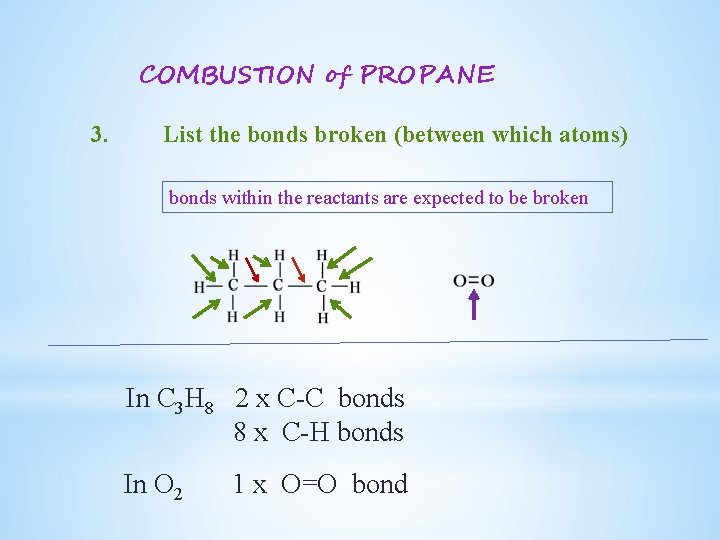
COMBUSTION of PROPANE 3. List the bonds broken (between which atoms) bonds within the reactants are expected to be broken In C 3 H 8 2 x C-C bonds 8 x C-H bonds In O 2 1 x O=O bond

COMBUSTION of PROPANE The numbers and types of bonds within the reactants which are expected to be broken are… In C 3 H 8 2 x C-C bonds 8 x C-H bonds In O 2 1 x O=O bond However, we need to check the coefficient in front of each reactant (look at the balanced equation) There are 5 moles of O 2 reacting with each mole of propane Therefore, in 5 x O 2 5 x O=O bonds

COMBUSTION of PROPANE 4. Find the Bond Dissociation Energies (BDE) associated for each bond (from Table 4. 4) BDE’s for C-C bonds: 356 k. J/mole C-H bonds: 436 k. J/mole O=O bonds: 498 k. J/mole

COMBUSTION of PROPANE Remember, there are 2 x C-C bonds 8 x C-H bonds 5 x O=O bonds (after balancing the equation) Here is the energy required to break all the bonds mentioned above: 2 x 356 k. J/mole = 712 k. J 8 x 436 k. J/mole = 3488 k. J 5 x 498 k. J/mole = 2490 k. J TOTAL: 6690 k. J

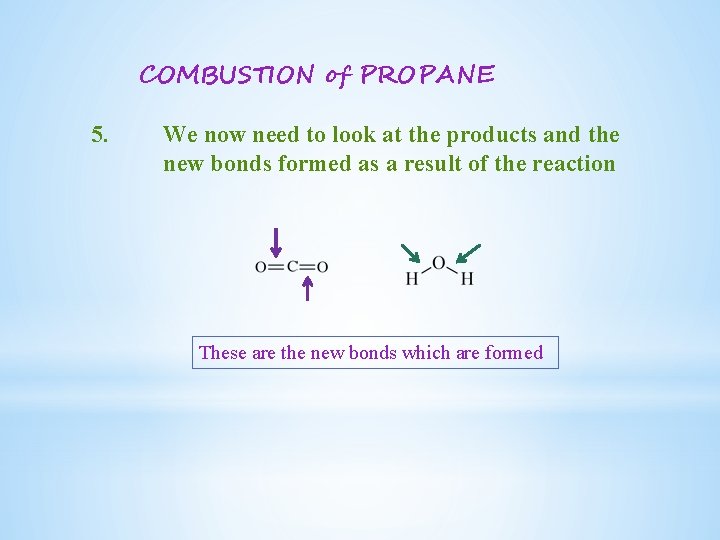
COMBUSTION of PROPANE 5. We now need to look at the products and the new bonds formed as a result of the reaction These are the new bonds which are formed

COMBUSTION of PROPANE new bonds formed within the products In CO 2 2 x C=O bonds In H 2 O 2 x O-H bonds However, we need to check the coefficient in front of each reactant (look at the balanced equation) There are 3 moles of CO 2 being formed (for each mole of propane) and 4 moles of H 2 O therefore In 3 x CO 2 In 4 x H 2 O 3 x 2 x C=O bonds 4 x 2 x O-H bonds

COMBUSTION of PROPANE 6. Find the Bond Dissociation Energies (BDE) associated for each bond being formed (from Table 4. 4) BDE’s for C=O bonds: 803 k. J/mole O-H bonds: 467 k. J/mole

COMBUSTION of PROPANE Remember, there are 3 x 2 x C=O bonds 4 x 2 x O-H bonds being formed (after balancing the equation) Here is the energy released when all the bonds mentioned above are formed: 6 x 803 k. J/mole = 4818 k. J 8 x 467 k. J/mole = 3736 k. J TOTAL: 8554 k. J

COMBUSTION of PROPANE 7. Subtract the total energy released from the total energy required to break the bonds to determine the heat of reaction, DH DH = 8554 k. J - 6690 k. J = 1864 k. J Let’s focus on the units now: This is 1864 k. J per mole of propane, C 3 H 8 undergoing complete combustion

COMBUSTION of PROPANE 8. What if we wish to determine the heat of reaction, DH, per gram of propane, C 3 H 8 undergoing complete combustion In 1 mole of C 3 H 8 there are 44 g of C 3 H 8 Therefore, the DH value we calculated previously is associated with 44 g of C 3 H 8 DH = 1864 k. J per 44 g of propane undergoing complete combustion

COMBUSTION of PROPANE If 44 g of C 3 H 8 releases 1864 k. J of energy, then 1. 0 g of C 3 H 8 will release 1/44 of that amount DH = 1864/44 k. J per 1. 0 g of propane = 42. 4 k. J/g of propane viewing the following units together might further clarify the type of calculation involved in converting the amount of energy from per mole to per gram