Combining materials for compositematerial cars Ford initiated research

Combining materials for composite-material cars • Ford initiated research at a time when they took a look at making cars from composite materials. • Graphite-epoxy is too expensive, glassepoxy is not stiff enough. • Grosset, L. , Venkataraman, S. , and Haftka, R. T. , “Genetic optimization of two-material composite laminates, ” Proceedings, 16 th ASC Technical Meeting, Blacksburg, VA, September 2001

Multi-material laminate • “Materials”: one material = 1 ply ( matrix or fiber materials) E. g. : glass-epoxy, graphite-epoxy, Kevlar-epoxy… • Use two materials in order to combine high efficiency (stiffness) and low cost • Graphite-epoxy: very stiff but expensive; glass-epoxy: less stiff, less expensive • Objective: use graphite-epoxy only where most efficient, use glass-epoxy for the remaining plies

Multi-criterion optimization • Two competing objective functions: WEIGHT and COST • Design variables: – number of plies – ply orientations – ply materials • No single design minimizes weight and cost simultaneously: A design is Pareto-optimal (non-dominated) if there is no design for which both Weight and Cost are lower • Goal: construct the trade-off curve between weight and cost (set of Pareto-optimal designs, also called Pareto front)

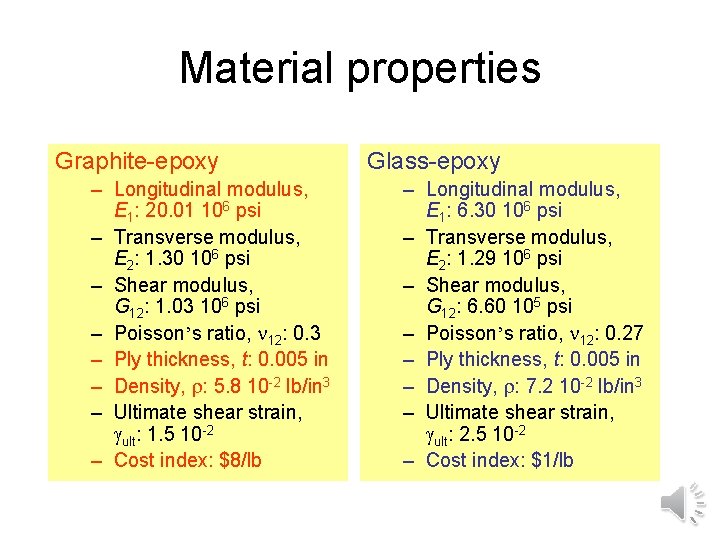
Material properties Graphite-epoxy – Longitudinal modulus, E 1: 20. 01 106 psi – Transverse modulus, E 2: 1. 30 106 psi – Shear modulus, G 12: 1. 03 106 psi – Poisson’s ratio, 12: 0. 3 – Ply thickness, t: 0. 005 in – Density, : 5. 8 10 -2 lb/in 3 – Ultimate shear strain, ult: 1. 5 10 -2 – Cost index: $8/lb Glass-epoxy – Longitudinal modulus, E 1: 6. 30 106 psi – Transverse modulus, E 2: 1. 29 106 psi – Shear modulus, G 12: 6. 60 105 psi – Poisson’s ratio, 12: 0. 27 – Ply thickness, t: 0. 005 in – Density, : 7. 2 10 -2 lb/in 3 – Ultimate shear strain, ult: 2. 5 10 -2 – Cost index: $1/lb

Optimization problem • Minimize weight and cost of a 30”x 36” plate • By changing ply orientations and material mi • subject to a frequency constraint:

Constructing the Pareto tradeoff curve • Simple method: weighting method. A composite function is constructed by combining the 2 objectives: W: weight C: cost : weighting parameter (0 1) • A succession of optimizations with varying from 0 to 1 is solved. The set of optimum designs builds up the Pareto trade-off curve • This is not a fool-proof approach (Why? ), and it is time consuming. Genetic algorithms provide a shortcut.

Multi-material Genetic Algorithm • Two variables for each ply: – Fiber orientation – Material • Each laminate is represented by 2 strings: – Orientation string – Material string • Example: [45/0/30/0/90] is represented by: – Orientation: – Material: 45 -0 -30 -0 -90 2 -2 -1 • GA maximizes fitness: Fitness = -F 1: graphite-epoxy 2: glass-epoxy

Simple vibrating plate problem • Minimize the weight (W) and cost (C) of a 36”x 30” rectangular laminated plate • 19 possible ply angles from 0 to 90 in 5 degree step • Constraints: – Balanced laminate (for each + ply, there must be a - ply in the laminate) – first natural frequency > 25 Hz Frequency calculated using Classical Lamination Theory

How constraints are enforced • Balance constraint hard coded in the strings: stacks of ± are used Example: (45 -0 -30 -25 -90) represents [± 45/0/± 30/± 25/90]s • Frequency constraint is incorporated into the objective function by a penalty, which is proportional to the constraint violation

Genetic operators • • • Roulette wheel selection based on rank Two-point crossover Mutation and permutation Ply deletion and addition Operators apply to each chromosome individually. • Best individual passed to the next generation (elitist)

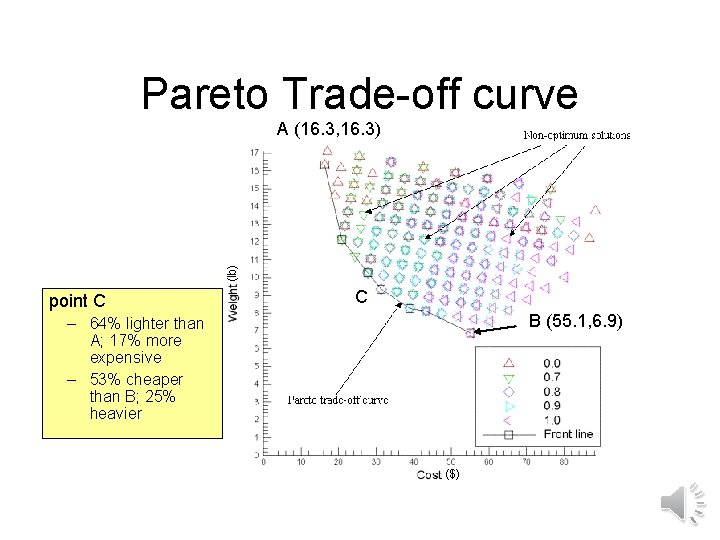
Pareto Trade-off curve (lb) A (16. 3, 16. 3) point C C B (55. 1, 6. 9) – 64% lighter than A; 17% more expensive – 53% cheaper than B; 25% heavier ($)

Optimum laminates • Cost minimization: [± 5010/0]s, cost = 16. 33, weight = 16. 33 • Weight minimization: [± 505/0]s, cost = 55. 12, weight = 6. 89 • Intermediate design: [± 502/± 505]s, cost = 27. 82, weight = 10. 28 Intermediate optimum laminates: sandwich-type laminates Midplane Graphite-epoxy as outer plies for a high frequency Glass-epoxy in the core layers to increase thickness

Problems two-material laminate • Check the reasonableness of the weight ratio of the two extreme laminates (16. 3/6. 9) with simple calculation. Solution • Illustrate the difference between crossover of two laminates when (a) the materials and angles are segregated into two chromosomes and (b) there is one string with the two numbers for each ply being together. Solution. • Why does the figure of the Pareto front not show values of alpha between 0 and 0. 7? Solution