Combined Variable Speed Limit and Lane Change Control

Combined Variable Speed Limit and Lane Change Control for Highway Traffic Yihang Zhang Department of Electrical Engineering University of Southern California Nov. 2016

Motivation • Mobility • Suppress demand of bottleneck • Smooth traffic flow • Dampen shockwaves, stop-and-go traffic • Safety • Warn drivers of hazardous roadway conditions • Reduce risk of crashes • Environment • Reduce pollution (tailpipe emissions: CO 2, CO, NOx, …) • Reduce energy (fuel) consumption
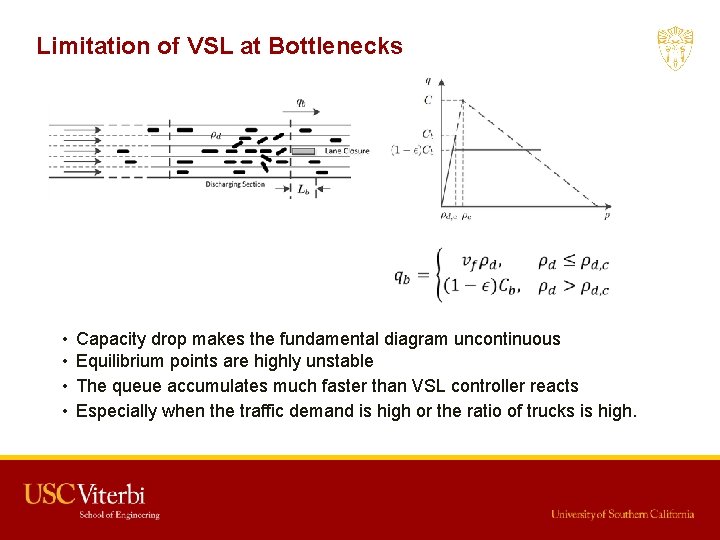
Limitation of VSL at Bottlenecks • • Capacity drop makes the fundamental diagram uncontinuous Equilibrium points are highly unstable The queue accumulates much faster than VSL controller reacts Especially when the traffic demand is high or the ratio of trucks is high.

Effect of Lane Change Control

Effect of Lane Change Control
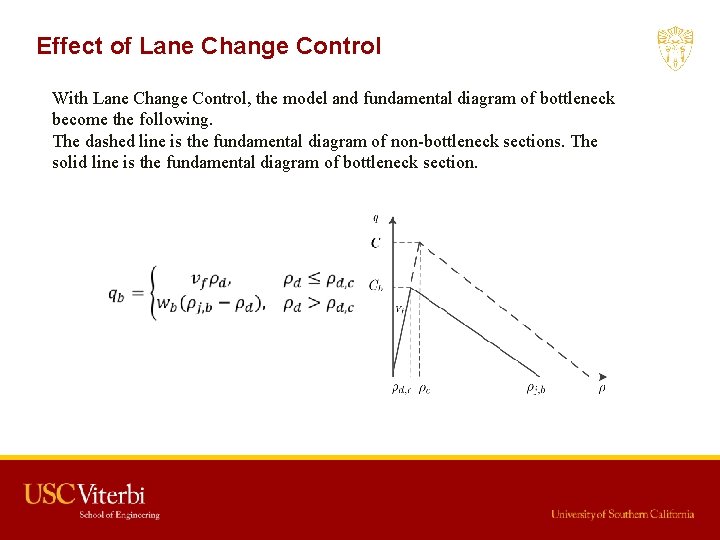
Effect of Lane Change Control With Lane Change Control, the model and fundamental diagram of bottleneck become the following. The dashed line is the fundamental diagram of non-bottleneck sections. The solid line is the fundamental diagram of bottleneck section.

Cell Transmission Model of Highway Traffic

Cell Transmission Model of Highway Traffic where

Design of the Combined VSL & LC Controller The design of the combined variable speed limit and lane change controller includes: (1) Design of the lane change controller to avoid capacity drop at the bottleneck (2) Design of the variable speed limit controller to stabilize the traffic flow on a desired level

Design of Lane Change Controller • LC control use overhead signs to provide lane change recommendations at the beginning of section N-M+1 through section N, in order to guarantee smooth traffic flow at bottleneck and avoid capacity drop. • For each lane, there are 4 possible types of LC recommendations: “Straight Ahead”, “Change to Left”, “Change to Right” and “Change to Either Way”

Design of Lane Change Controller Lane Change Recommendation Patterns: Proper lane change recommendation type Ri in lane i should help upstream vehicles to leave the closed lane and evenly distribute traffic flow to open lanes. 1. For i=1, 2, …, m, if Lane i is open, Ri = “Straight Ahead”; 2. For i = 1(i = m), if Lane i is closed, Ri = “Change to Left (Right)”; 3. For 1 < i < m, if Lane i is closed, Lane i − 1 and Lane i + 1 are both open, Ri = “Change to Either Way”; 4. For 1 < i < m, if Lane i is closed, Lane i − 1 (Lane i + 1) is closed and Lane i + 1 (Lane i − 1) is open, Ri = “Change to Left (Right)”; 5. For 1 < i < m, if Lane i is closed, Lane i − 1 and Lane i + 1 are both closed, then we check Ri− 1 and Ri+1. If Ri− 1 = Ri+1, then Ri = Ri− 1 = Ri+1, else if Ri− 1 ≠ Ri+1, Ri = “Change to Either Way”.
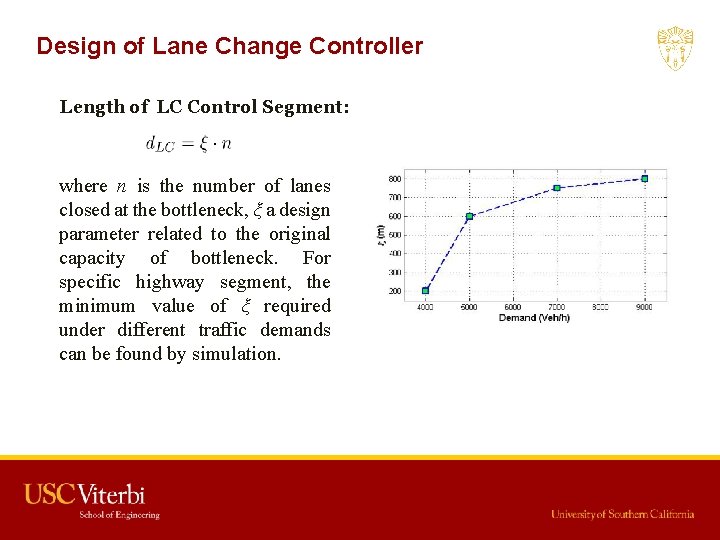
Design of Lane Change Controller Length of LC Control Segment: where n is the number of lanes closed at the bottleneck, ξ a design parameter related to the original capacity of bottleneck. For specific highway segment, the minimum value of ξ required under different traffic demands can be found by simulation.

Design of Lane Change Controller Length of LC Control Segment: LC signs is only deployed at the beginning of each section. We choose number of LC controlled sections M, such that

Desired Equilibrium Point For any equilibrium points in this system, we need
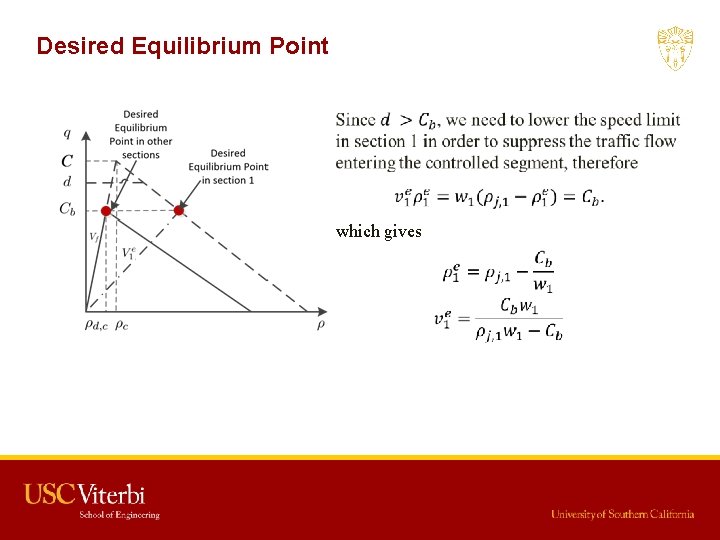
Desired Equilibrium Point which gives

Desired Equilibrium Point Consider the desired equilibrium point, the highway traffic system can be expressed as follows

Feedback Linearization VSL Controller We choose the following feedback controller

Feedback Linearization VSL Controller Then the closed-loop system becomes

Constraints on VSL Commands To ensure safety and drive acceptance, we apply following constraints to VSL command: • vi are made piecewise constant with respect to time t for driver acceptance • VSL commands vi are rounded to whole 5 mi/h numbers. • Lower and upper bounds are applied to VSL commands • The speed limit decrease should be within some threshold Cv > 0 between successive control periods and highway sections.
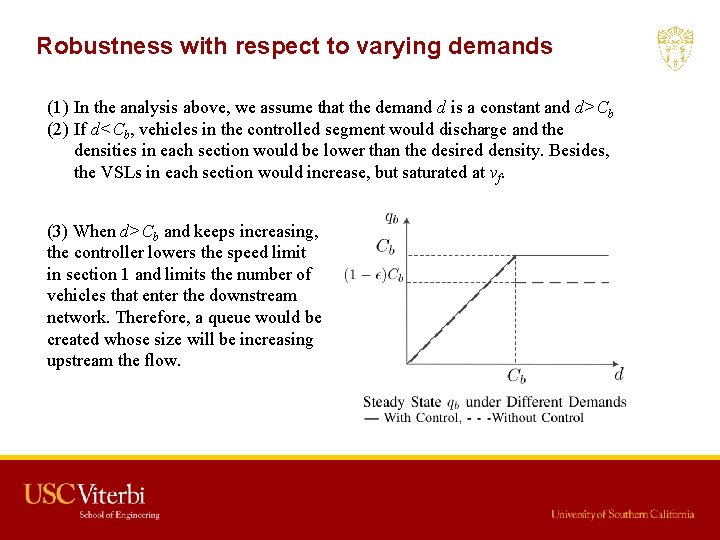
Robustness with respect to varying demands (1) In the analysis above, we assume that the demand d is a constant and d>Cb (2) If d<Cb, vehicles in the controlled segment would discharge and the densities in each section would be lower than the desired density. Besides, the VSLs in each section would increase, but saturated at vf. (3) When d>Cb and keeps increasing, the controller lowers the speed limit in section 1 and limits the number of vehicles that enter the downstream network. Therefore, a queue would be created whose size will be increasing upstream the flow.

Numerical Simulation Setup: 1. Simulation Network: 16 km-long southbound segment of I-710 freeway in California, whose normal capacity without an accident is about 6800 veh/h. 2. Incident Scenarios: We construct accident scenarios with different accident durations 3. Monte Carlo Simulation 10 sets of Monte Carlo simulation for each scenario in microscopic simulations.
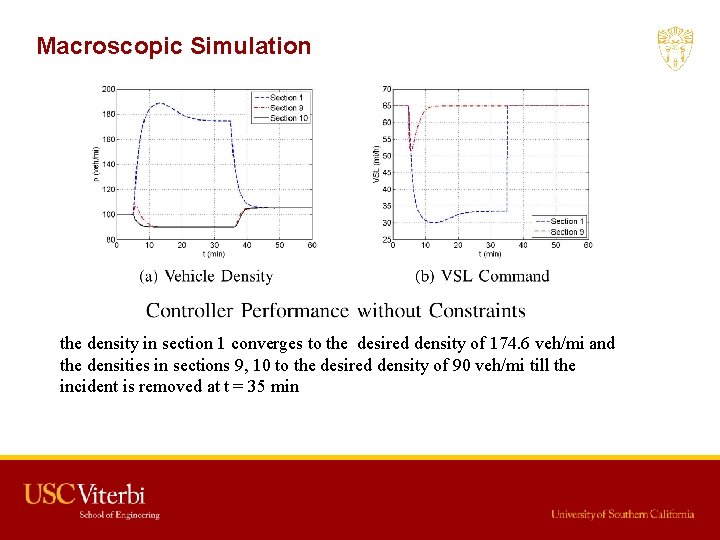
Macroscopic Simulation the density in section 1 converges to the desired density of 174. 6 veh/mi and the densities in sections 9, 10 to the desired density of 90 veh/mi till the incident is removed at t = 35 min
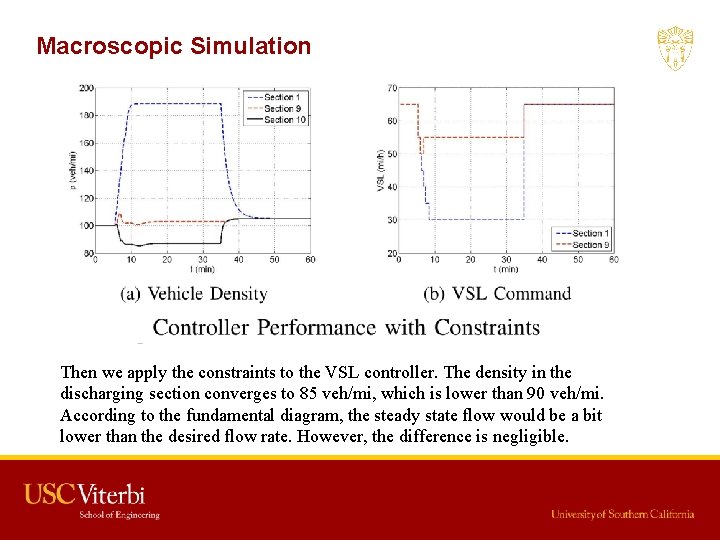
Macroscopic Simulation Then we apply the constraints to the VSL controller. The density in the discharging section converges to 85 veh/mi, which is lower than 90 veh/mi. According to the fundamental diagram, the steady state flow would be a bit lower than the desired flow rate. However, the difference is negligible.
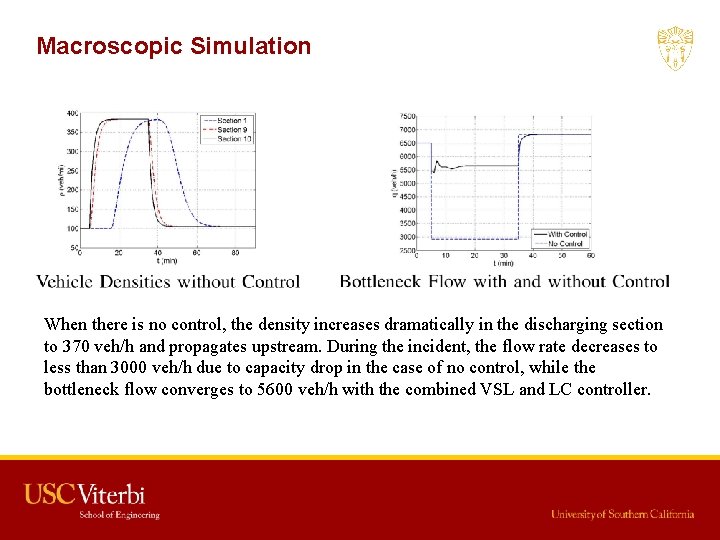
Macroscopic Simulation When there is no control, the density increases dramatically in the discharging section to 370 veh/h and propagates upstream. During the incident, the flow rate decreases to less than 3000 veh/h due to capacity drop in the case of no control, while the bottleneck flow converges to 5600 veh/h with the combined VSL and LC controller.
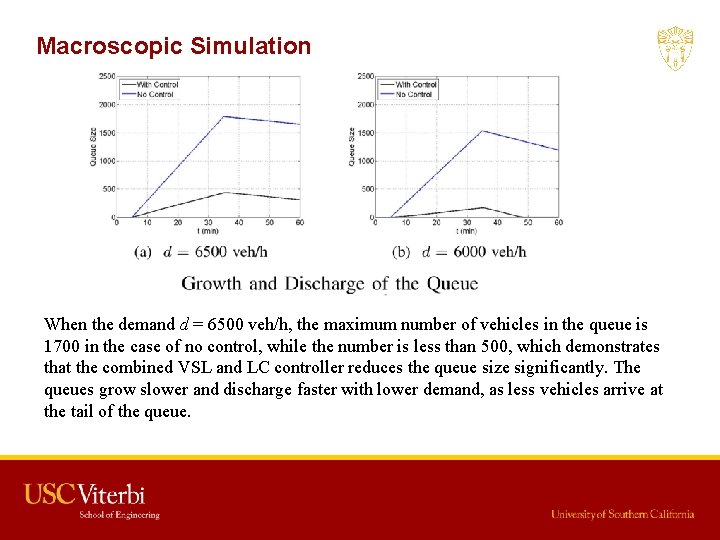
Macroscopic Simulation When the demand d = 6500 veh/h, the maximum number of vehicles in the queue is 1700 in the case of no control, while the number is less than 500, which demonstrates that the combined VSL and LC controller reduces the queue size significantly. The queues grow slower and discharge faster with lower demand, as less vehicles arrive at the tail of the queue.
Microscopic Simulation
Microscopic Simulation
Microscopic Simulation

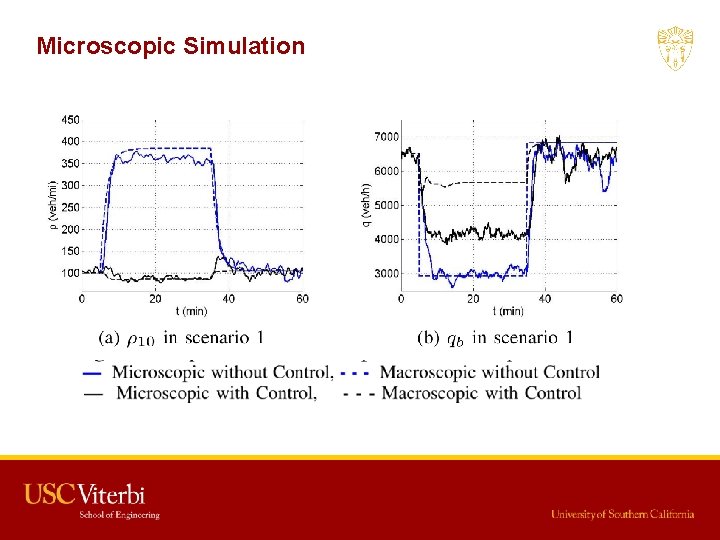
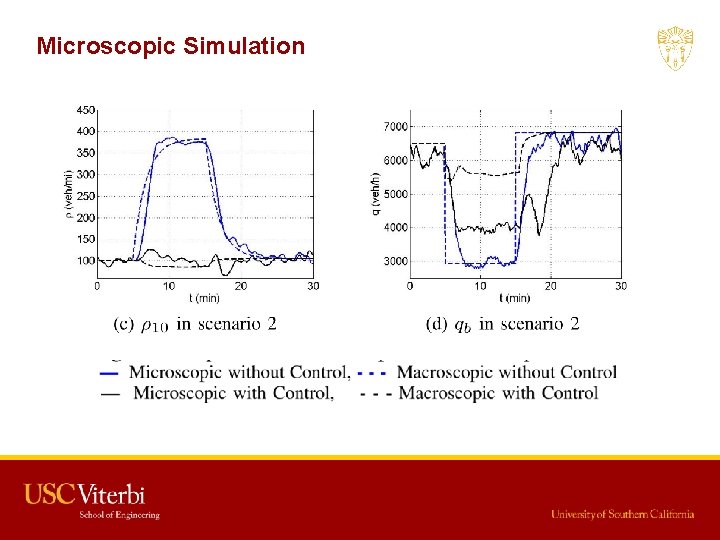
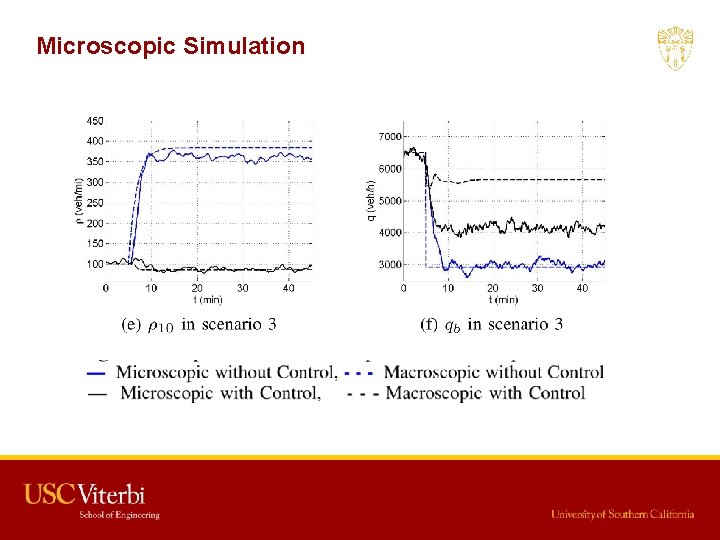
Microscopic Simulation Reasons of deviation of bottleneck flow under control between macroscopic simulation and microscopic simulation: (1) Modeling Error. The actual fundamental diagram is not perfectly triangular (2) Speed Limit Following Delay. The traffic flow needs time and space to accelerate to the desired speed limit. (3) Friction Effect. Drivers' fear of moving fast in the open lanes when an incident or slowly moving vehicles exist in neighboring lanes
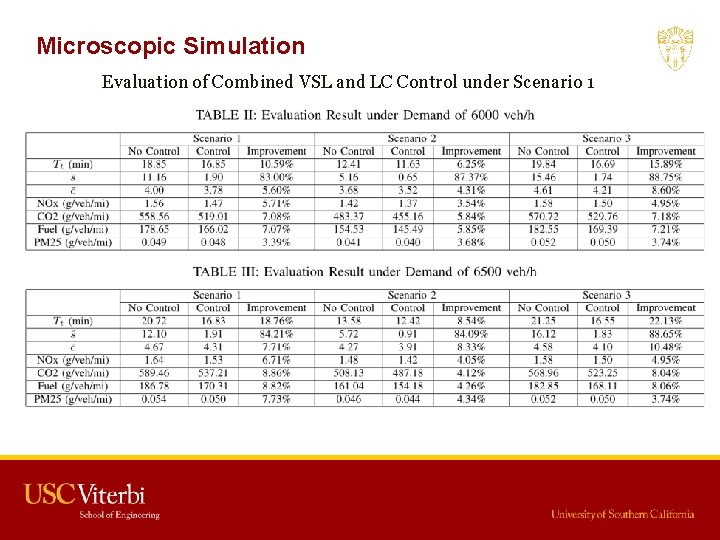
Microscopic Simulation Evaluation of Combined VSL and LC Control under Scenario 1

Microscopic Simulation Analysis of Evaluation Results • The combined VSL & LC control strategy reduces the travel time for each vehicle by 6. 25% - 22. 13%, number of stops by about 83% - 88. 75%, number of lane changes by 5. 6% -10. 48%, fuel consumption rate and CO 2 emission by 4. 26% - 8. 82%, NOx emission by 3. 54% - 6. 71%. Therefore, traffic mobility, safety and environment are all significantly improved. • The improvement on each measurement criteria in scenario 2 appears to be less significant than the other 2 scenarios, since the incident duration in scenario 2 is very short.

Conclusion • A combined variable speed limit and lane change control strategy for highway traffic is proposed. • LC control provides lane change recommendation in an open loop manner and is able to remove the capacity drop • A feedback linearization VSL controller is designed and is able to guarantee the stability of closed loop equilibrium point. • Certain constraints on the output of the VSL controller are imposed by taking into account driver responses. • Simulations of the traffic along I-710 with high truck ratio are used to demonstrate improvements under different scenarios.
- Slides: 32