Combined Fatigue Loading Mode Basquin curve Finite cycle

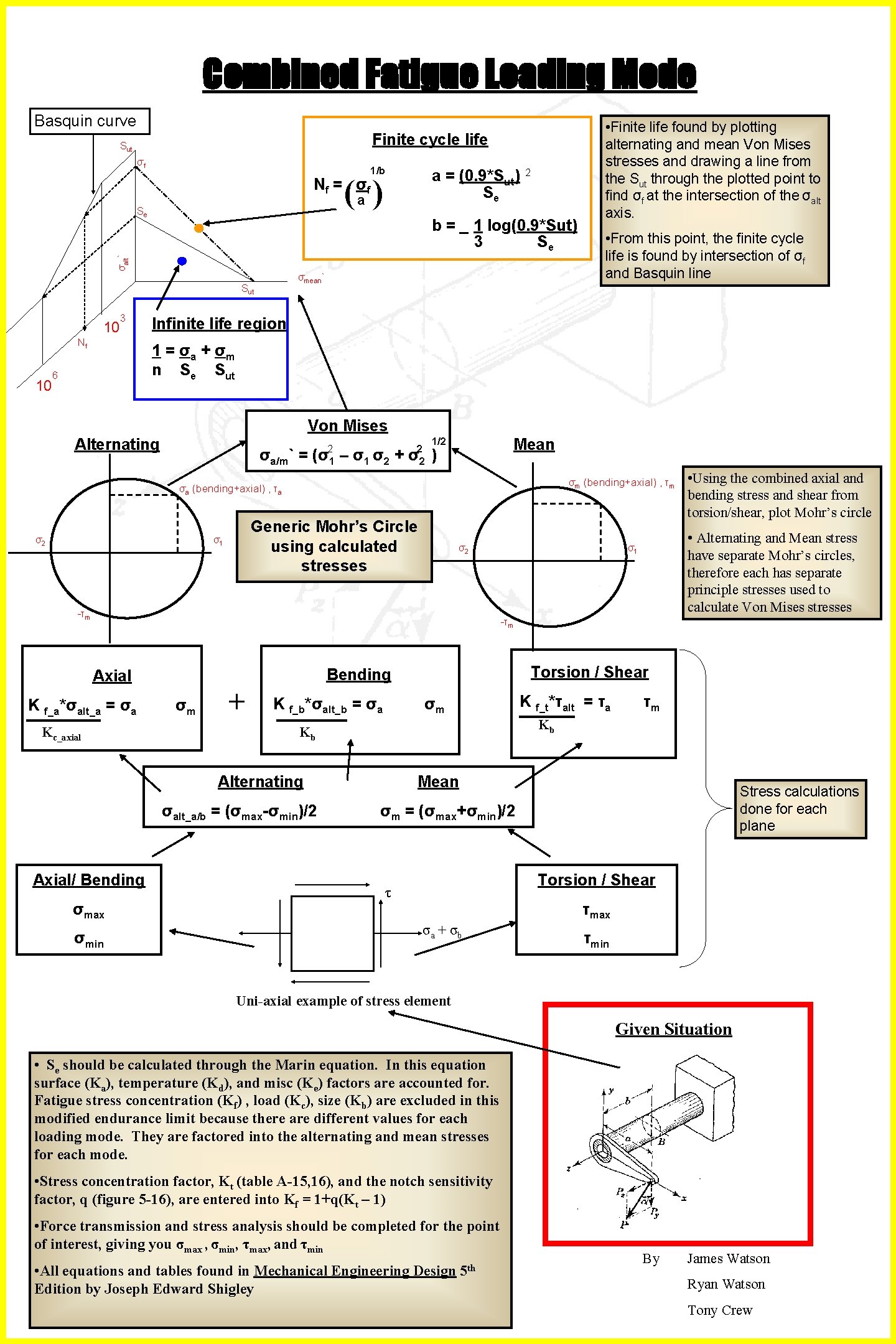
Combined Fatigue Loading Mode Basquin curve Finite cycle life Sut σf 1/b a = (0. 9*Sut) Se (a ) N f = σf Se σalt` b = _ 1 log(0. 9*Sut) 3 Se σmean` Sut 10 3 Nf 10 2 • Finite life found by plotting alternating and mean Von Mises stresses and drawing a line from the Sut through the plotted point to find σf at the intersection of the σalt axis. • From this point, the finite cycle life is found by intersection of σf and Basquin line Infinite life region 1 = σa + σm n Se Sut 6 Von Mises Alternating σa/m` = 2 (σ1 – σ1 σ2 + 2 σ2 1/2 Mean ) σm (bending+axial) , τm σa (bending+axial) , τa σ2 Generic Mohr’s Circle using calculated stresses σ1 σ2 -τm • Using the combined axial and bending stress and shear from torsion/shear, plot Mohr’s circle • Alternating and Mean stress have separate Mohr’s circles, therefore each has separate principle stresses used to calculate Von Mises stresses σ1 -τm K f_a*σalt_a = σa Kc_axial σm + K f_b*σalt_b = σa σmin τm Kb Kb σalt_a/b = (σmax-σmin)/2 σmax K f_t*τalt = τa σm Alternating Axial/ Bending Torsion / Shear Bending Axial Mean Stress calculations done for each plane σm = (σmax+σmin)/2 Torsion / Shear τ τmax σa + σ b τmin Uni-axial example of stress element Given Situation • Se should be calculated through the Marin equation. In this equation surface (Ka), temperature (Kd), and misc (Ke) factors are accounted for. Fatigue stress concentration (Kf) , load (Kc), size (Kb) are excluded in this modified endurance limit because there are different values for each loading mode. They are factored into the alternating and mean stresses for each mode. • Stress concentration factor, Kt (table A-15, 16), and the notch sensitivity factor, q (figure 5 -16), are entered into Kf = 1+q(Kt – 1) • Force transmission and stress analysis should be completed for the point of interest, giving you σmax , σmin, τmax, and τmin • All equations and tables found in Mechanical Engineering Design Edition by Joseph Edward Shigley 5 th By James Watson Ryan Watson Tony Crew