Combine Like Terms and Distributive Property Combine Like

Combine Like Terms and Distributive Property

Combine Like Terms and Distributive Property In this lesson, you will be shown how to combine like terms along with using the distributive property.

Terms in an algebraic expression are separated by addition or subtraction signs. How many terms are in this expression? So, what are like terms? Like terms are terms that look alike.

More specifically, Like Terms are terms that have the same variable raised to the same power (exponent). Now, let’s give this a try.

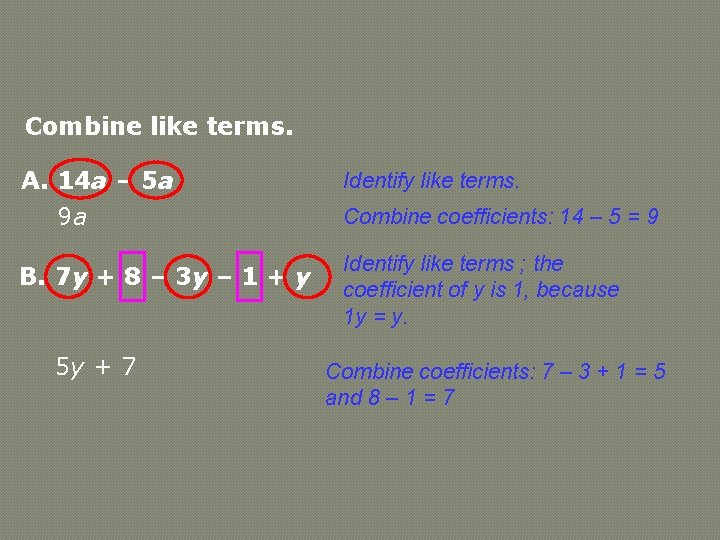
Combine like terms. A. 14 a – 5 a 9 a Identify like terms. B. 7 y + 8 – 3 y – 1 + y Identify like terms ; the coefficient of y is 1, because 1 y = y. 5 y + 7 Combine coefficients: 14 – 5 = 9 Combine coefficients: 7 – 3 + 1 = 5 and 8 – 1 = 7

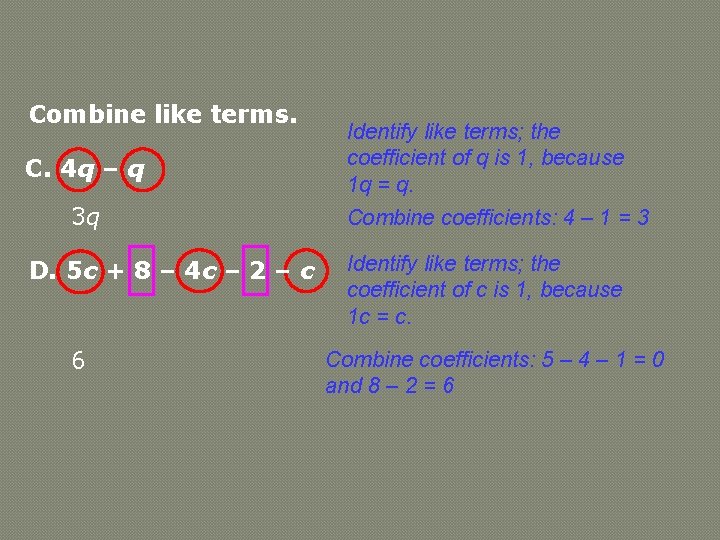
Combine like terms. C. 4 q – q 3 q D. 5 c + 8 – 4 c – 2 – c 6 Identify like terms; the coefficient of q is 1, because 1 q = q. Combine coefficients: 4 – 1 = 3 Identify like terms; the coefficient of c is 1, because 1 c = c. Combine coefficients: 5 – 4 – 1 = 0 and 8 – 2 = 6

Combine like terms. E. 4 m + 9 n – 2 F. 5 m * 7 m – 8 + 4 35 m – 4 No like terms.

Remember, to simplify an expression means to perform all possible operations, including combining like terms. In other words, simplify means solve!

The Distributive Property is an algebra property which is used to multiply a single term and two or more terms inside a set of parentheses. For any numbers a, b, and c, a(b + c) = a(b) + a(c) and a(b – c) = a(b) – a(c)

Distribute A. 6(x - 3) 6 x - 18 B. 2(y + 1) 2 y + 2 C. 3(a - 1) 3 a – 3

Now we will use the distributive property first, then combine like terms second.

1. Simplify 6(5 + n) – 2 n 6(5) + 6(n) – 2 n Distributive Property. 30 + 6 n – 2 n Multiply. 30 + 4 n Combine coefficients 6 – 2 = 4.

2. Simplify 3(c + 7) – c 3(c) + 3(7) – c Distributive Property. 3 c + 21 – c Multiply. 2 c + 21 Combine coefficients 3 – 1 = 2.

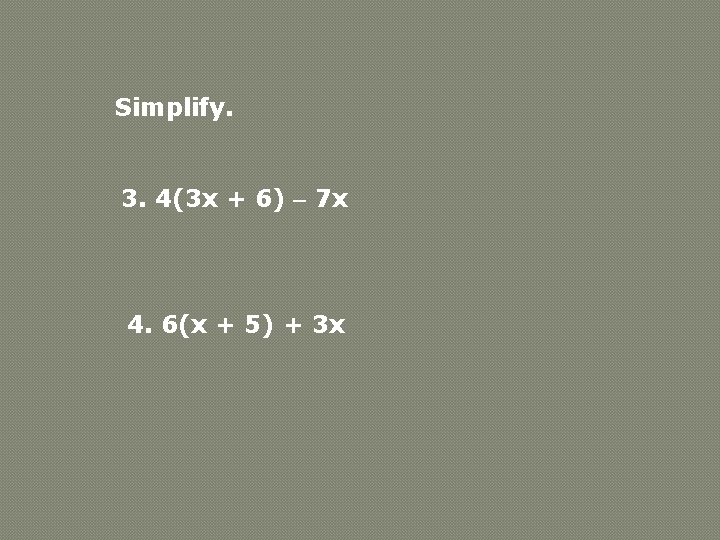
Simplify. 3. 4(3 x + 6) 7 x 4. 6(x + 5) + 3 x

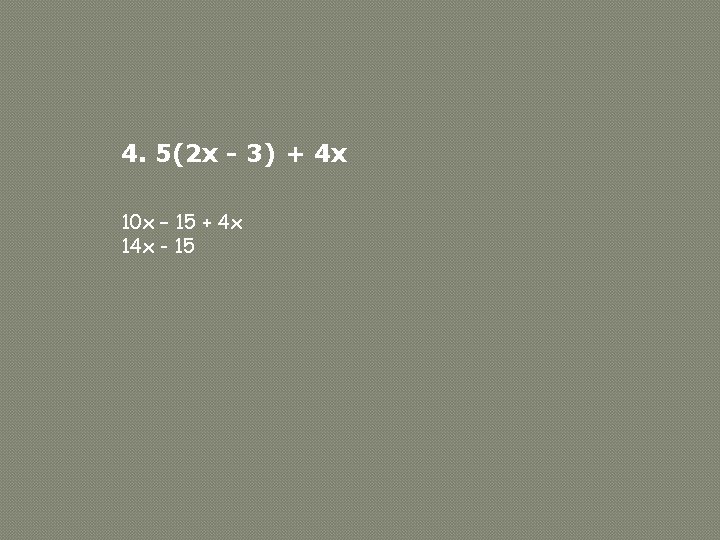
4. 5(2 x - 3) + 4 x 10 x – 15 + 4 x 14 x - 15