Combinatorial Logic Design Principles ECGR 2181 Chapter 4

Combinatorial Logic Design Principles ECGR 2181 Chapter 4 Notes Reading: Chapter 4 Logic System Design I 4 -1

Boolean algebra a. k. a. “switching algebra” – deals with boolean values -- 0, 1 Positive-logic convention – analog voltages LOW, HIGH --> 0, 1 Negative logic -- seldom used Signal values denoted by variables (X, Y, FRED, etc. ) Logic System Design I 4 -2

Boolean operators Complement: X¢ (opposite of X) AND: X×Y OR: X+Y binary operators, described functionally by truth table. Axiomatic definition: A 1 -A 5, A 1¢-A 5¢ (Axiom = A well-formed formula which is taken to be true without proof in the construction of a theory. ) Logic System Design I 4 -3

More definitions Literal: a variable or its complement – X, X¢, FRED¢, CS_L Expression: literals combined by AND, OR, parentheses, complementation – – X+Y P×Q×R A+B×C ((FRED × Z¢) + CS_L × A × B¢ × C + Q 5) × RESET¢ Equation: Variable = expression – P = ((FRED × Z¢) + CS_L × A × B¢ × C + Q 5) × RESET¢ Logic System Design I 4 -4

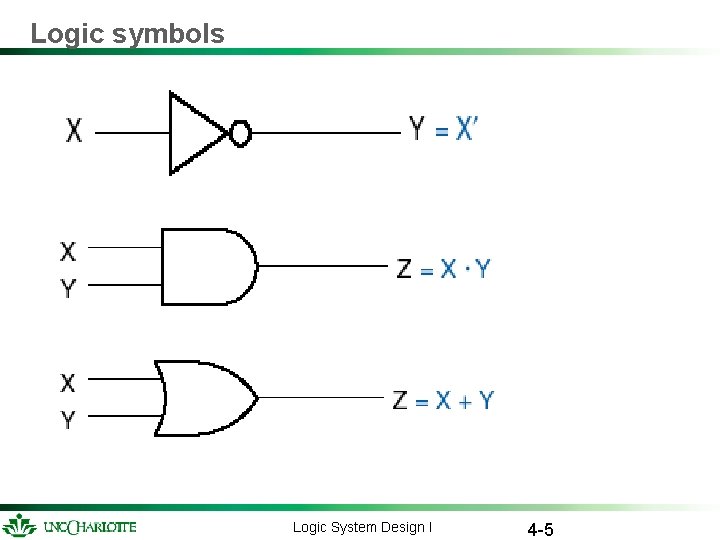
Logic symbols Logic System Design I 4 -5

Theorems Proofs by perfect induction Logic System Design I 4 -6

More Theorems Logic System Design I 4 -7

N-variable Theorems Prove using finite induction Logic System Design I 4 -8

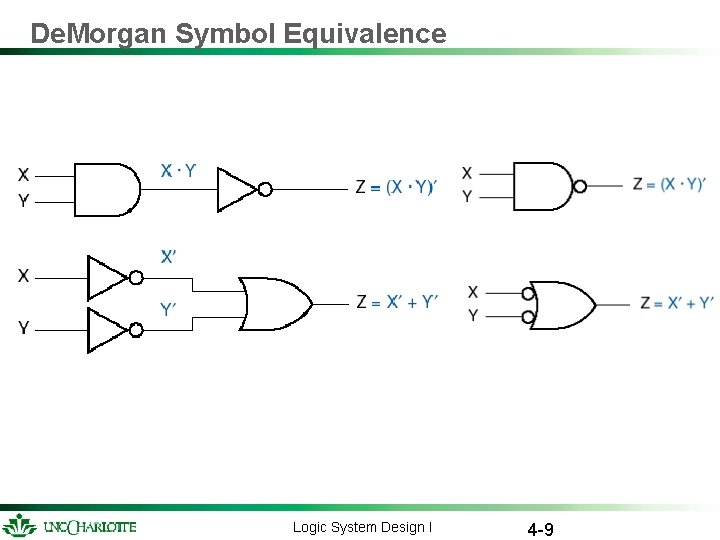
De. Morgan Symbol Equivalence Logic System Design I 4 -9

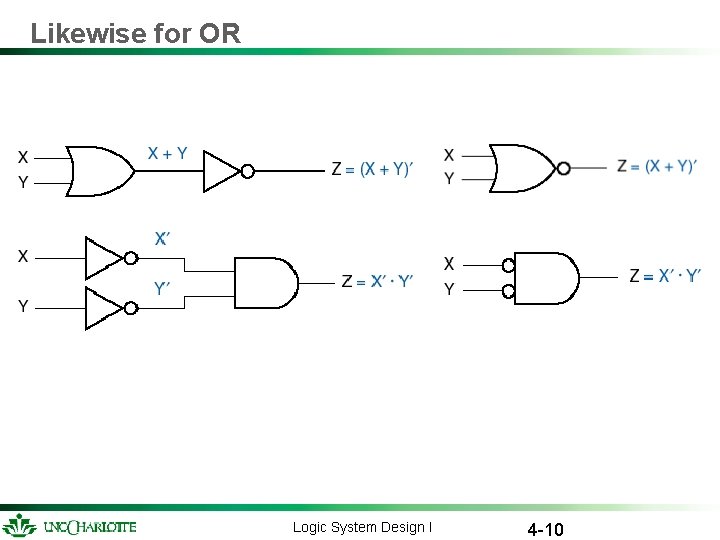
Likewise for OR Logic System Design I 4 -10

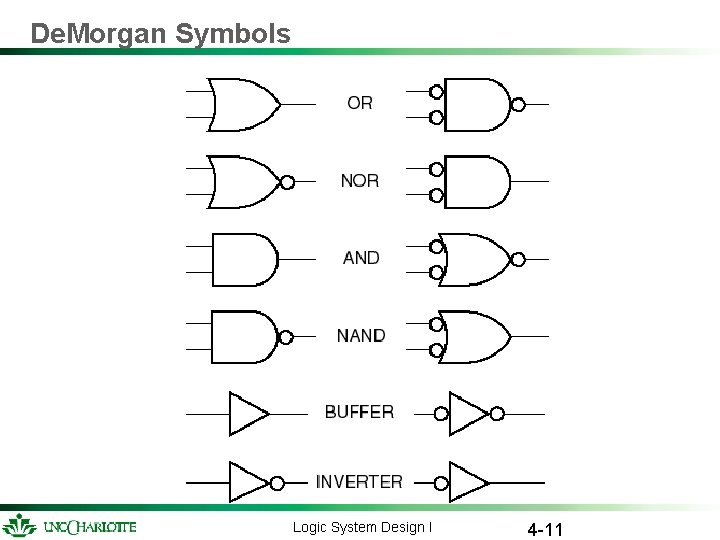
De. Morgan Symbols Logic System Design I 4 -11

Even more definitions (Sec. 4. 1. 6) Product term Sum-of-products expression Sum term Product-of-sums expression Normal term Minterm (n variables) Maxterm (n variables) Logic System Design I 4 -12

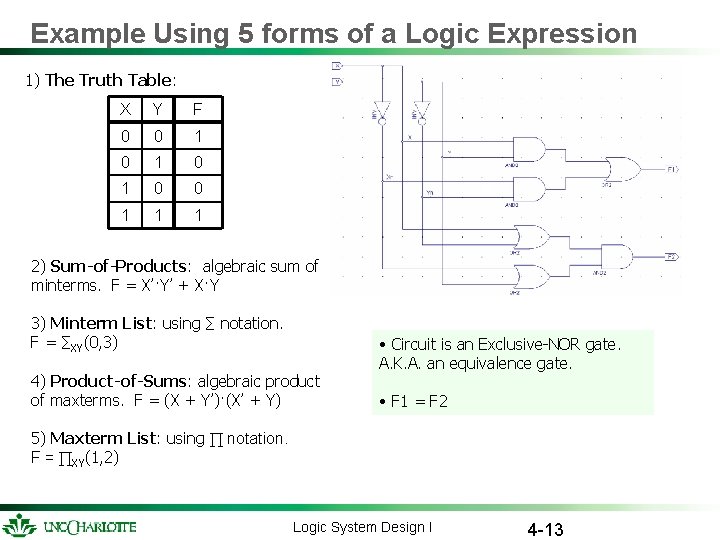
Example Using 5 forms of a Logic Expression 1) The Truth Table: X Y F 0 0 1 0 1 0 0 1 1 1 2) Sum-of-Products: algebraic sum of minterms. F = X’·Y’ + X·Y 3) Minterm List: using ∑ notation. F = ∑XY(0, 3) 4) Product-of-Sums: algebraic product of maxterms. F = (X + Y’)·(X’ + Y) • Circuit is an Exclusive-NOR gate. A. K. A. an equivalence gate. • F 1 = F 2 5) Maxterm List: using ∏ notation. F = ∏XY(1, 2) Logic System Design I 4 -13

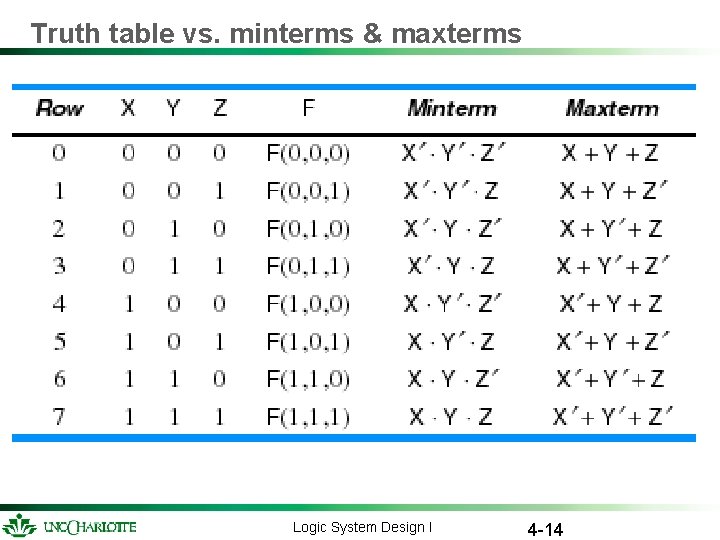
Truth table vs. minterms & maxterms Logic System Design I 4 -14

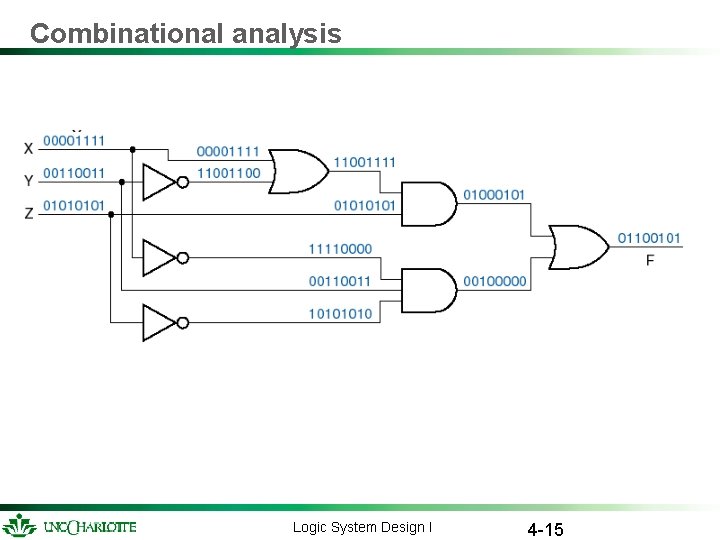
Combinational analysis Logic System Design I 4 -15

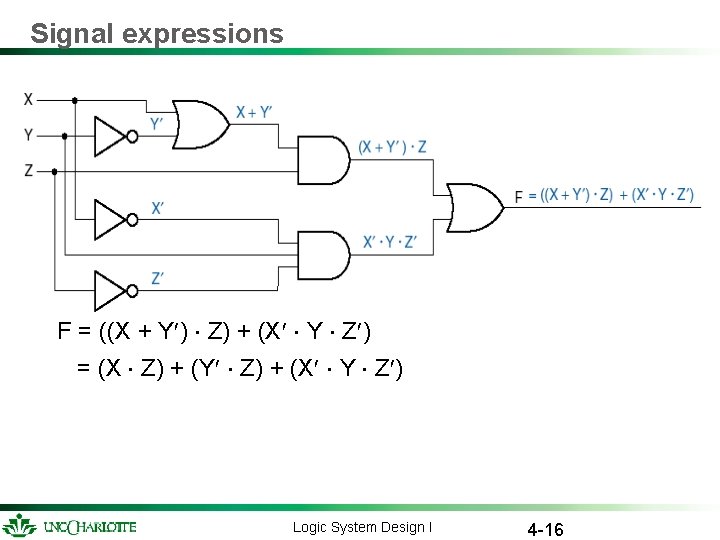
Signal expressions Multiply out: F = ((X + Y¢) × Z) + (X¢ × Y × Z¢) = (X × Z) + (Y¢ × Z) + (X¢ × Y × Z¢) Logic System Design I 4 -16

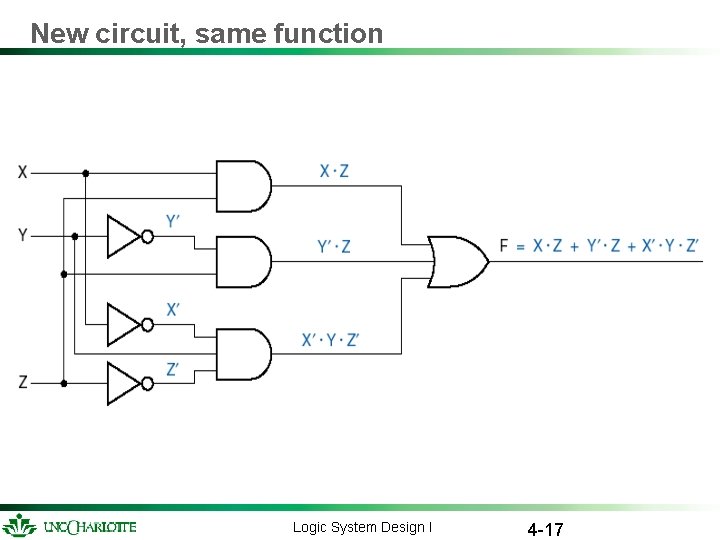
New circuit, same function Logic System Design I 4 -17

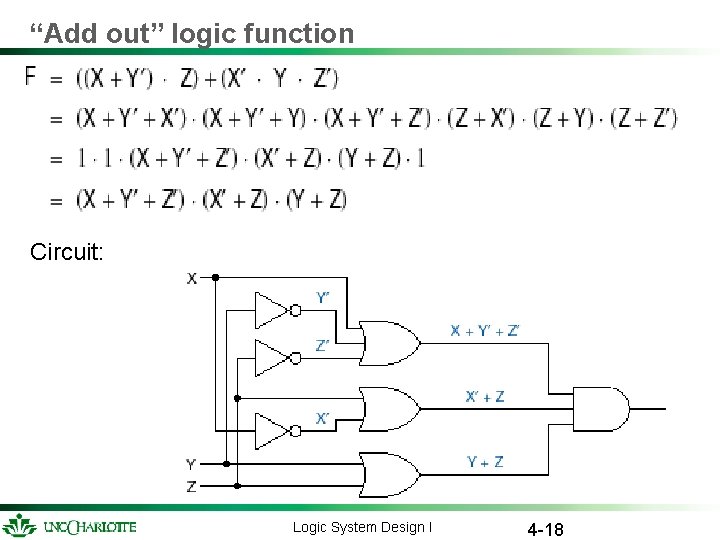
“Add out” logic function Circuit: Logic System Design I 4 -18

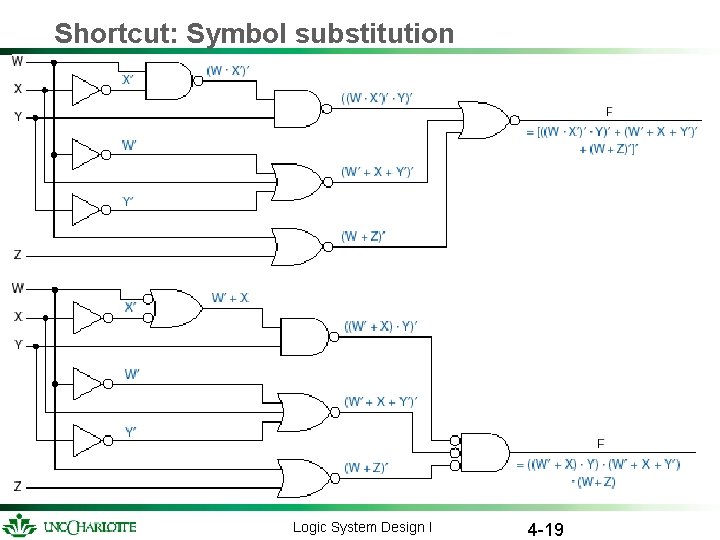
Shortcut: Symbol substitution Logic System Design I 4 -19

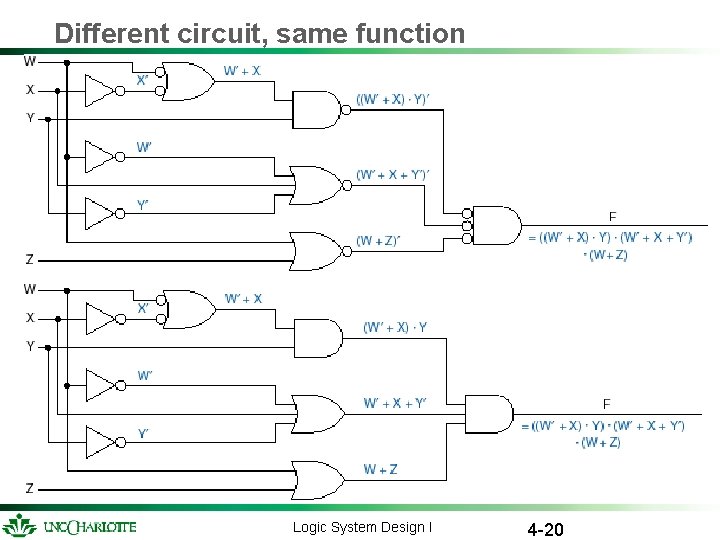
Different circuit, same function Logic System Design I 4 -20

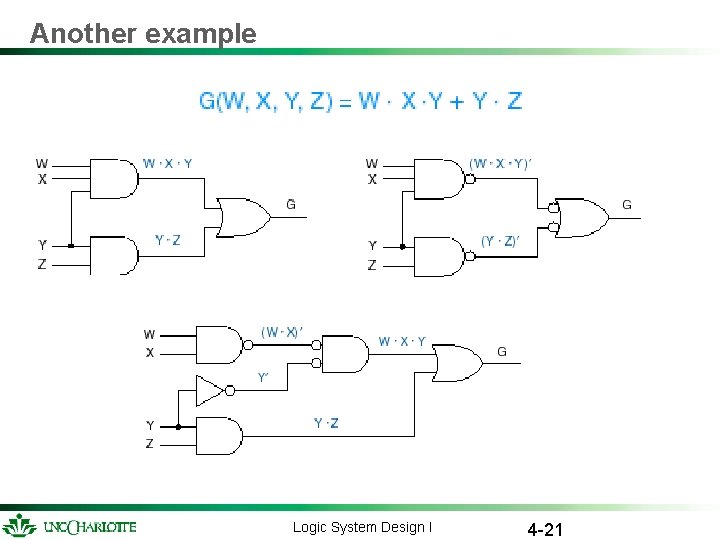
Another example Logic System Design I 4 -21

Combinational-Circuit Analysis Combinational circuits -- outputs depend only on current inputs (not on history). Kinds of combinational analysis: – exhaustive (truth table) – algebraic (expressions) – simulation / test bench • Write functional description in HDL • Define test conditions / test vecors • Compare circuit output with functional description (or knowngood realization) Logic System Design I 4 -22

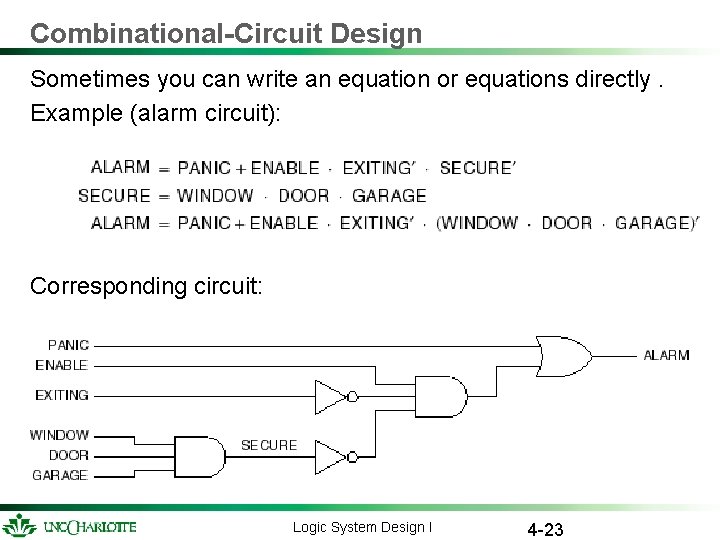
Combinational-Circuit Design Sometimes you can write an equation or equations directly. Example (alarm circuit): Corresponding circuit: Logic System Design I 4 -23

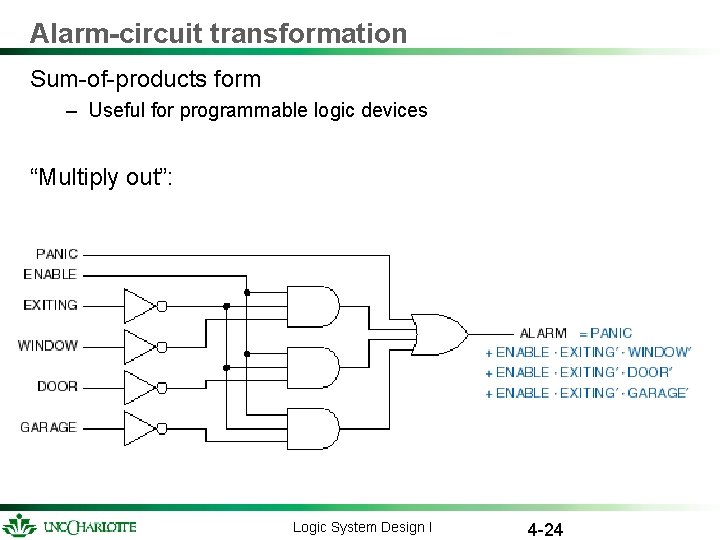
Alarm-circuit transformation Sum-of-products form – Useful for programmable logic devices “Multiply out”: Logic System Design I 4 -24

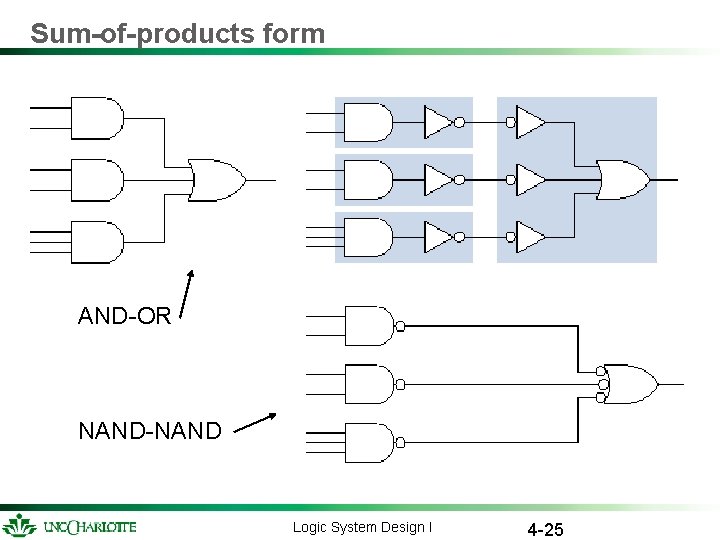
Sum-of-products form AND-OR NAND-NAND Logic System Design I 4 -25

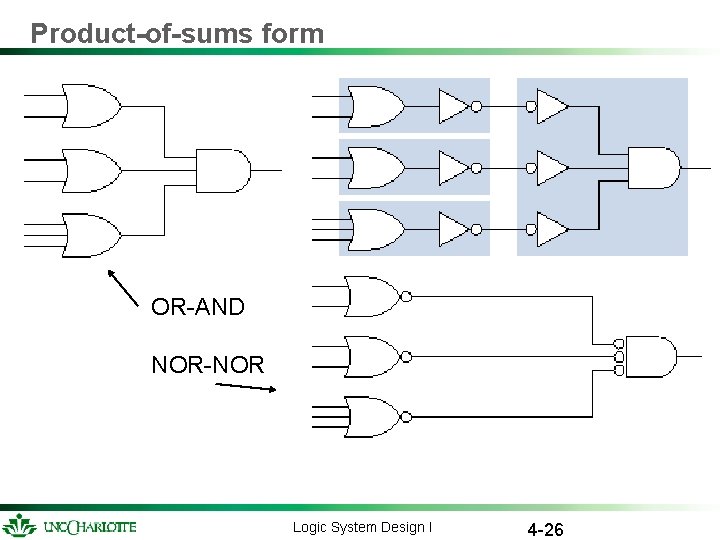
Product-of-sums form OR-AND NOR-NOR Logic System Design I 4 -26

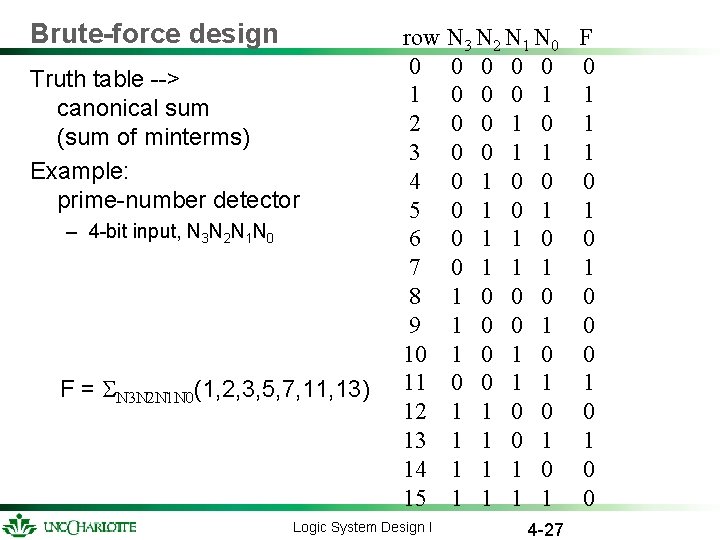
Brute-force design Truth table --> canonical sum (sum of minterms) Example: prime-number detector – 4 -bit input, N 3 N 2 N 1 N 0 F = N 3 N 2 N 1 N 0(1, 2, 3, 5, 7, 11, 13) row N 3 N 2 N 1 N 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1 10 1 0 11 0 0 1 1 12 1 1 0 0 13 1 1 0 1 14 1 1 1 0 15 1 1 Logic System Design I 4 -27 F 0 1 1 1 0 1 0 0

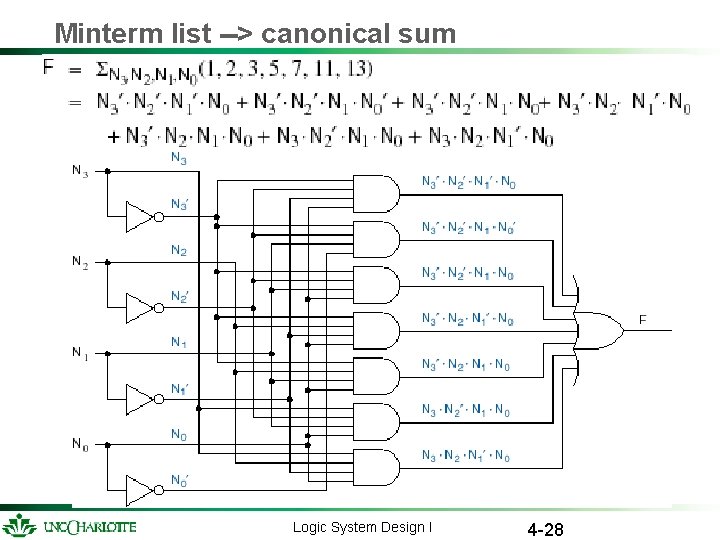
Minterm list --> canonical sum Logic System Design I 4 -28

Algebraic simplification Theorem T 8, Reduce number of gates and gate inputs Logic System Design I 4 -29

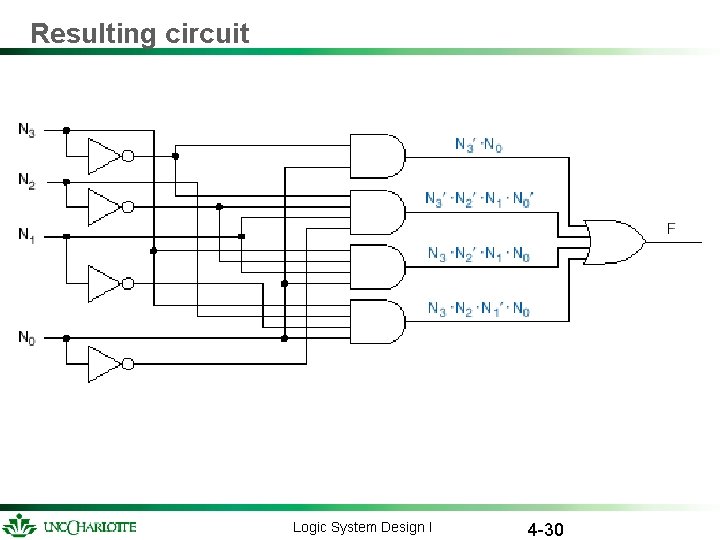
Resulting circuit Logic System Design I 4 -30

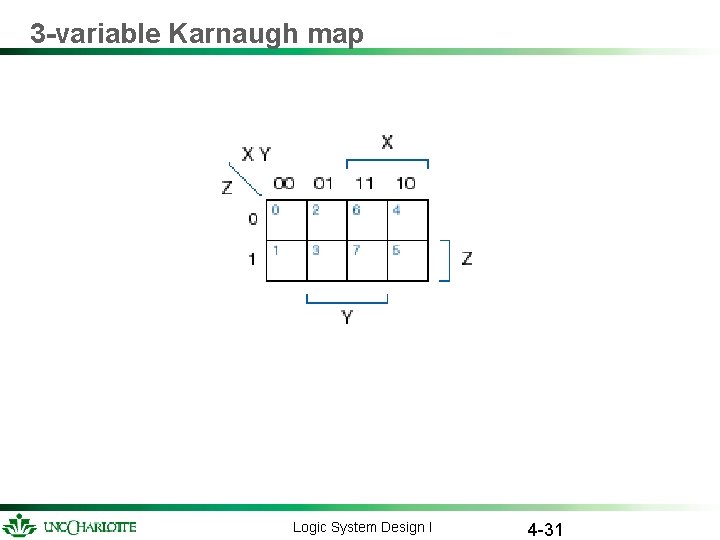
3 -variable Karnaugh map Logic System Design I 4 -31

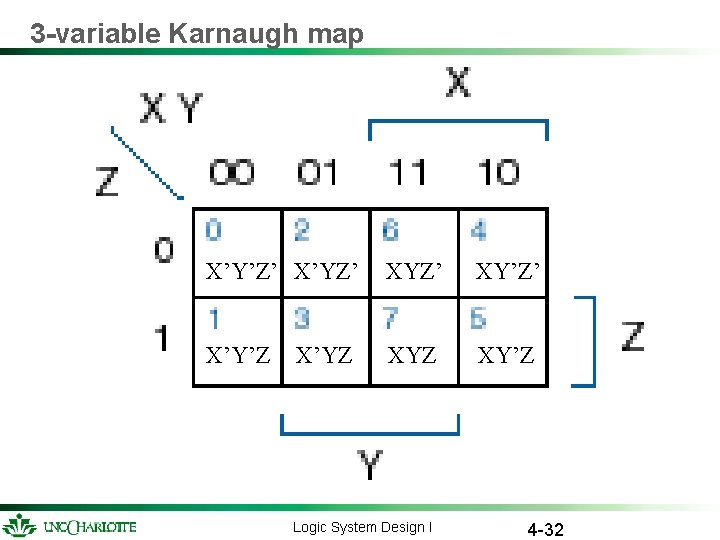
3 -variable Karnaugh map X’Y’Z’ X’YZ’ XY’Z’ X’Y’Z XY’Z X’YZ Logic System Design I 4 -32

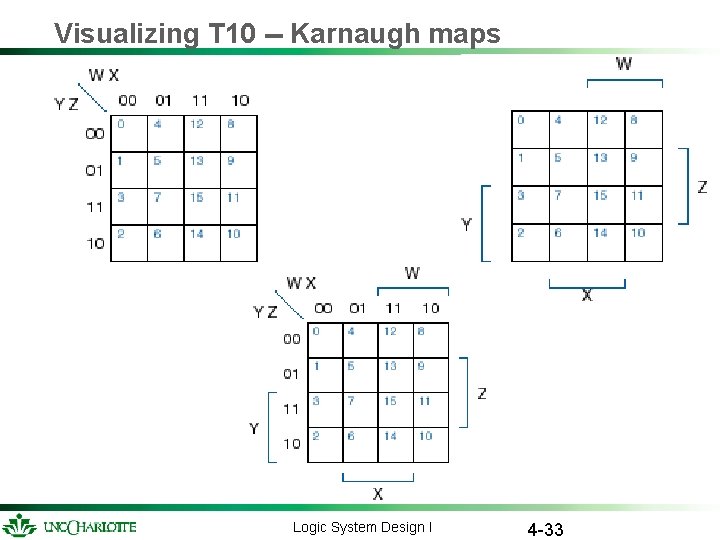
Visualizing T 10 -- Karnaugh maps Logic System Design I 4 -33

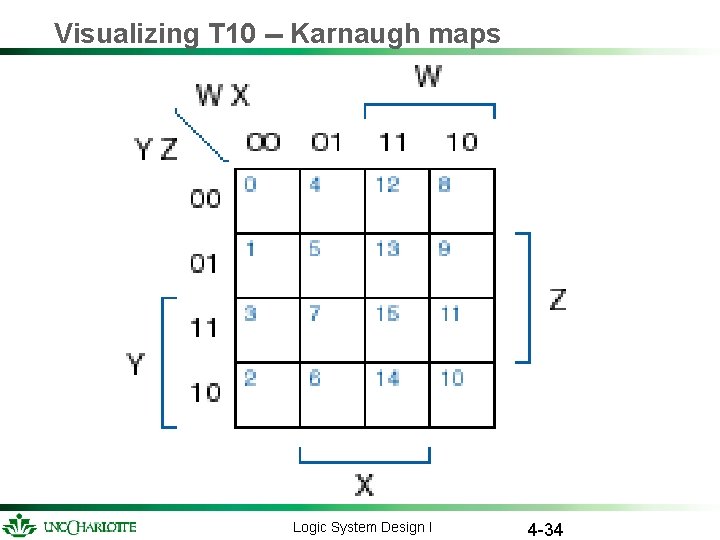
Visualizing T 10 -- Karnaugh maps Logic System Design I 4 -34

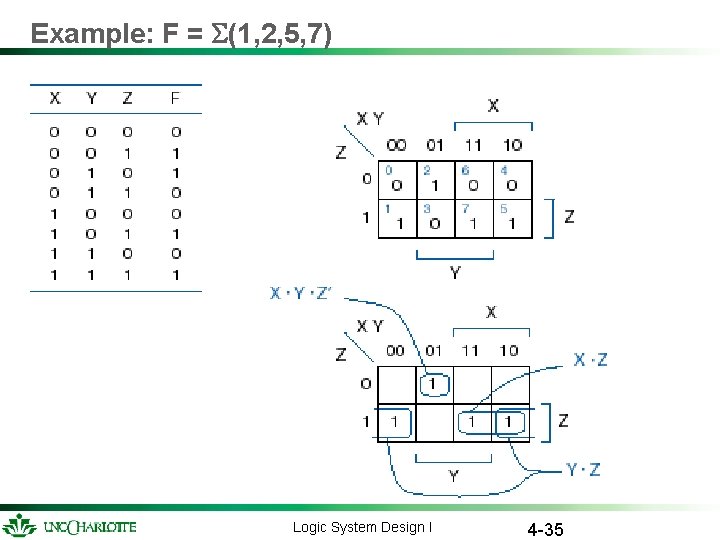
Example: F = S(1, 2, 5, 7) Logic System Design I 4 -35

Karnaugh-map usage Plot 1 s corresponding to minterms of function. Circle largest possible rectangular sets of 1 s. – # of 1 s in set must be power of 2 – OK to cross edges Read off product terms, one per circled set. – Variable is 1 ==> include variable – Variable is 0 ==> include complement of variable – Variable is both 0 and 1 ==> variable not included Circled sets and corresponding product terms are called “prime implicants” Minimum number of gates and gate inputs Logic System Design I 4 -36

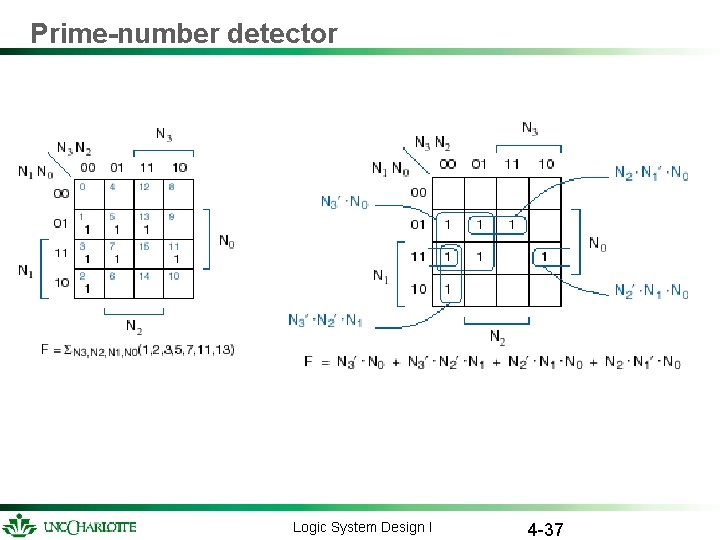
Prime-number detector Logic System Design I 4 -37

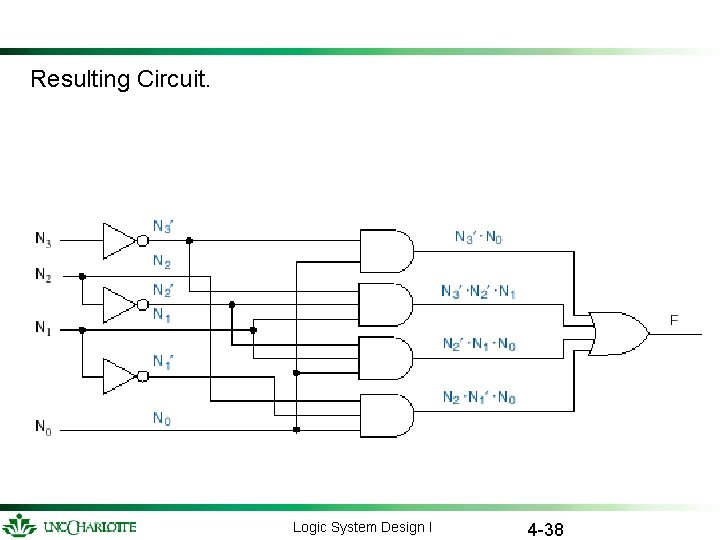
Resulting Circuit. Logic System Design I 4 -38

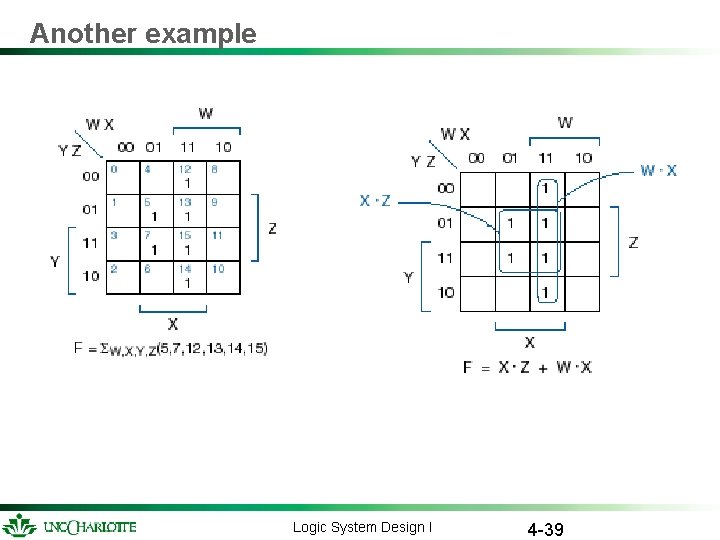
Another example Logic System Design I 4 -39

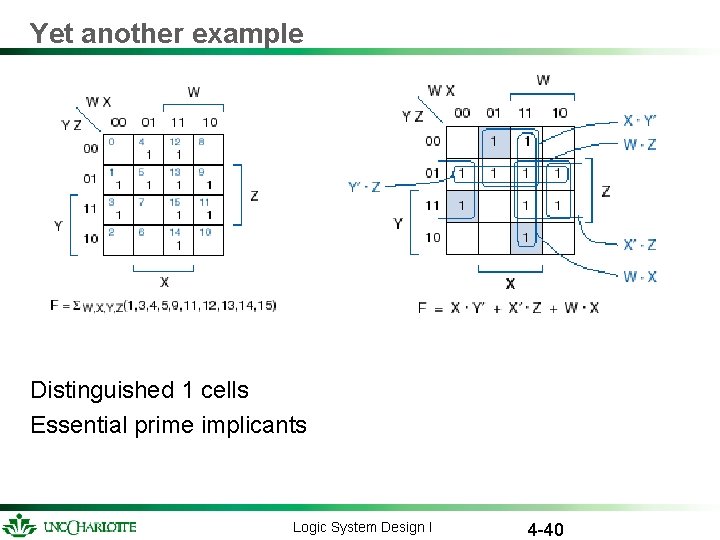
Yet another example Distinguished 1 cells Essential prime implicants Logic System Design I 4 -40

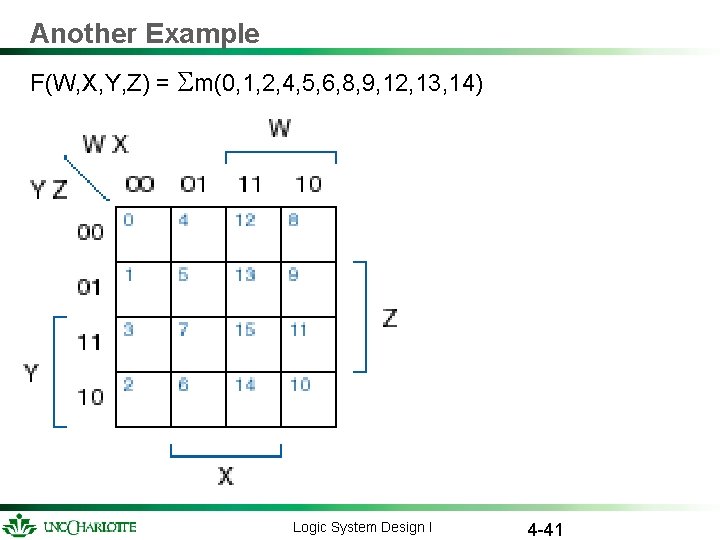
Another Example F(W, X, Y, Z) = m(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) Logic System Design I 4 -41

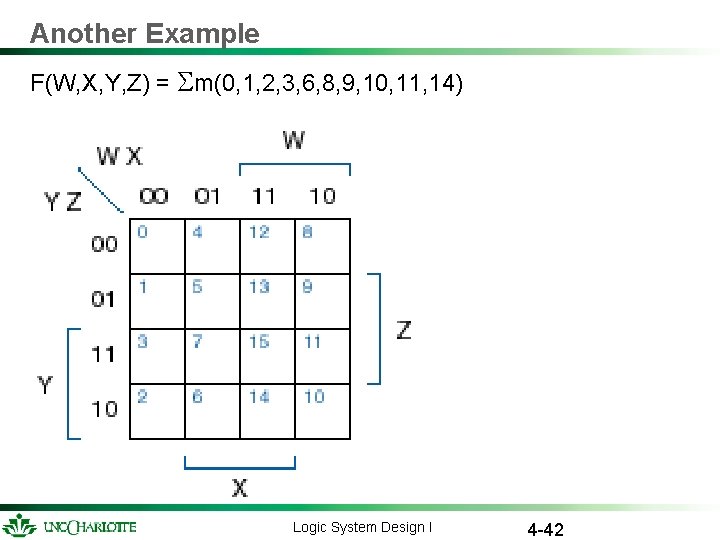
Another Example F(W, X, Y, Z) = m(0, 1, 2, 3, 6, 8, 9, 10, 11, 14) Logic System Design I 4 -42

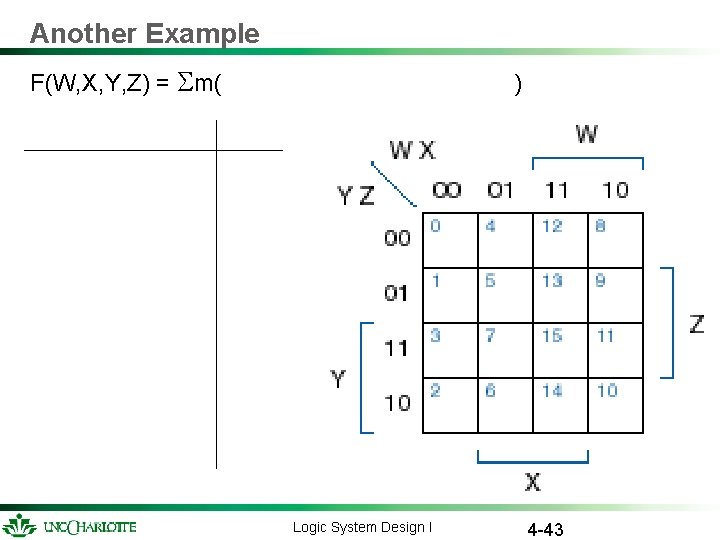
Another Example F(W, X, Y, Z) = m( ) Logic System Design I 4 -43

Don’t Cares Logic System Design I 4 -44

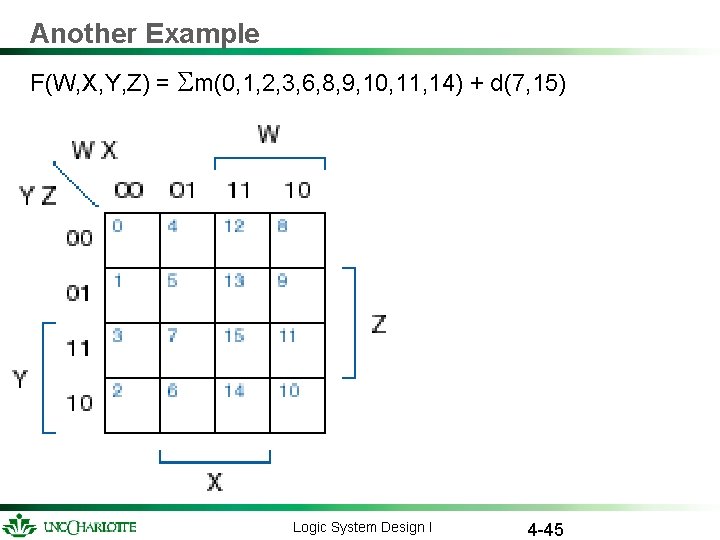
Another Example F(W, X, Y, Z) = m(0, 1, 2, 3, 6, 8, 9, 10, 11, 14) + d(7, 15) Logic System Design I 4 -45

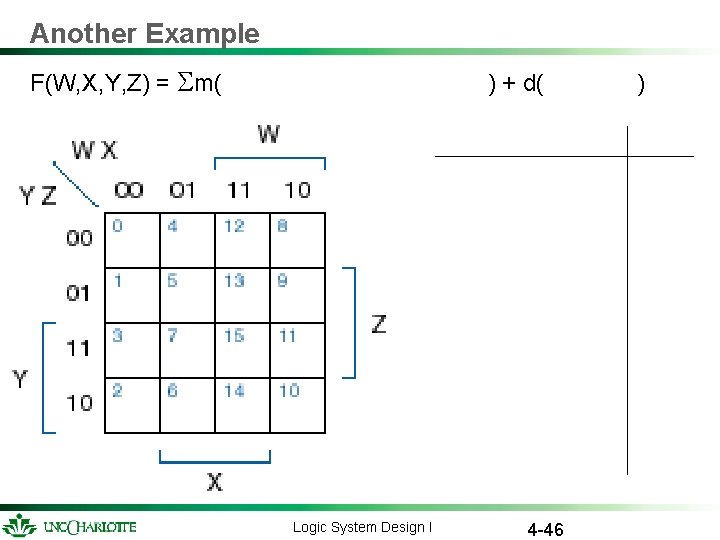
Another Example F(W, X, Y, Z) = m( ) + d( Logic System Design I 4 -46 )

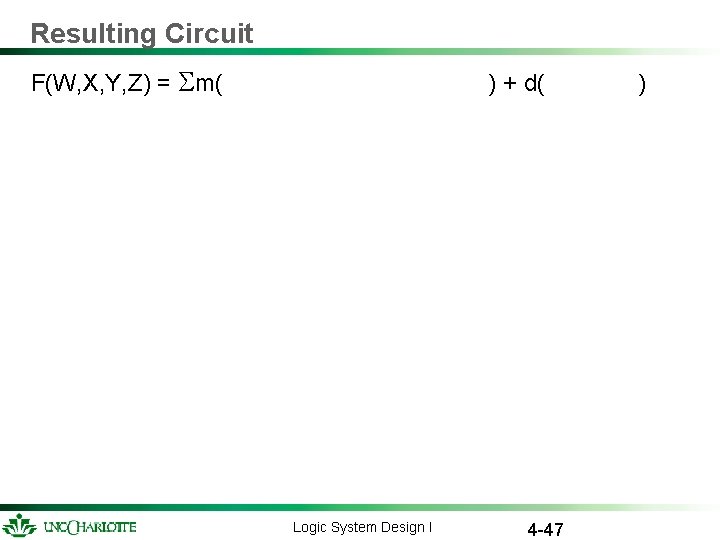
Resulting Circuit F(W, X, Y, Z) = m( ) + d( Logic System Design I 4 -47 )

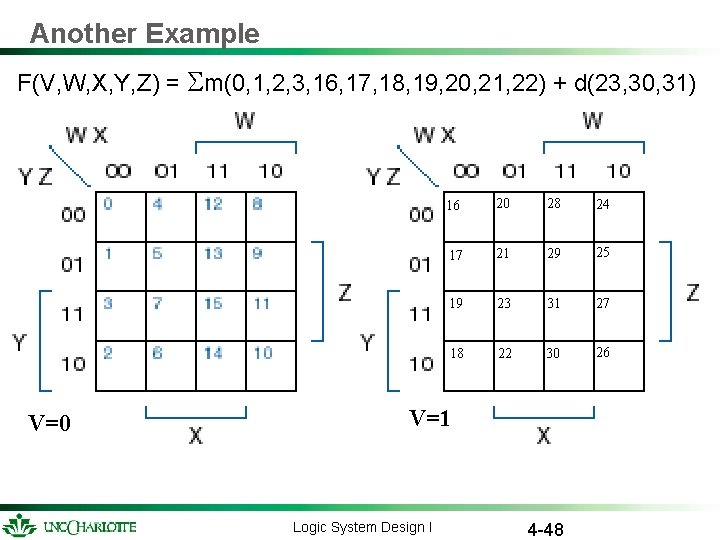
Another Example F(V, W, X, Y, Z) = m(0, 1, 2, 3, 16, 17, 18, 19, 20, 21, 22) + d(23, 30, 31) V=0 16 20 28 24 17 21 29 25 19 23 31 27 18 22 30 26 V=1 Logic System Design I 4 -48

Resulting Circuit F(V, W, X, Y, Z) = m(0, 1, 2, 3, 16, 17, 18, 19, 20, 21, 22) + d(23, 30, 31) Logic System Design I 4 -49

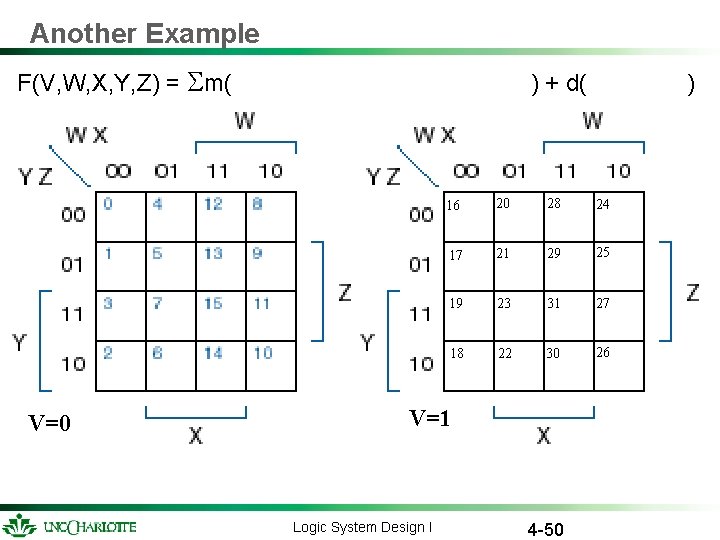
Another Example F(V, W, X, Y, Z) = m( V=0 ) + d( 16 20 28 24 17 21 29 25 19 23 31 27 18 22 30 26 V=1 Logic System Design I ) 4 -50

Current Logic Design Lots more than 6 inputs -- can’t use Karnaugh maps Use software to synthesize logic expressions and minimize logic Hardware Description Languages -- VHDL and Verilog Logic System Design I 4 -51