Combinations Permutations Essentials Permutations Combinations So thats how

Combinations & Permutations

Essentials: Permutations & Combinations (So that’s how we determine the number of possible samples!) l Definitions: Permutation; Factorial; Combination. l What a Factorial is and how to use it. l Ability to determine the number of permutations or combinations resulting from a stated situation. l Extras here: Tree diagrams & the multiplication rule.

Factorials l The Factorial of a number is the multiplication of that number by every smaller number down to 1. l The Factorial Notation is n!, where n represents the number and the “!” indicates the factorial process. l Note the following: By definition 0! = 1 l Example: 8! = 8 * 7 *6 * 5 * 4 * 3 * 2 *1 = 40, 320

Permutations l A Permutation is an arrangement of n objects in a specific order using r objects at a time.

Permutations: Examples l Example: A news program has time to present 2 of four available news stories. How many ways can the evening news be set up? Checking the process: If we let A, B, C, D represent the four shows, then the possible show orders would be: AB BA CA DA AC BC CB DB AD BD CD DC Twelve (12) possible presentations where order matters.

Combinations l A combination is the selection of r objects from n objects without regard to order.

Combinations: Examples l Example: A news program has time to present 2 of four available news stories. How many different sets of stories can be presented on the evening news? Checking the process: If we let A, B, C, D represent the four shows, then the possible show orders would be: AB BA CA DA AC BC CB DB AD BD CD DC However, AB and BA represent the presentation of the same two stories. If order does not matter, one of these two may be deleted. Repeating the process results in: AB, AC, AD, BC, BD, CD, Six (6) different presentations where order does not matter.

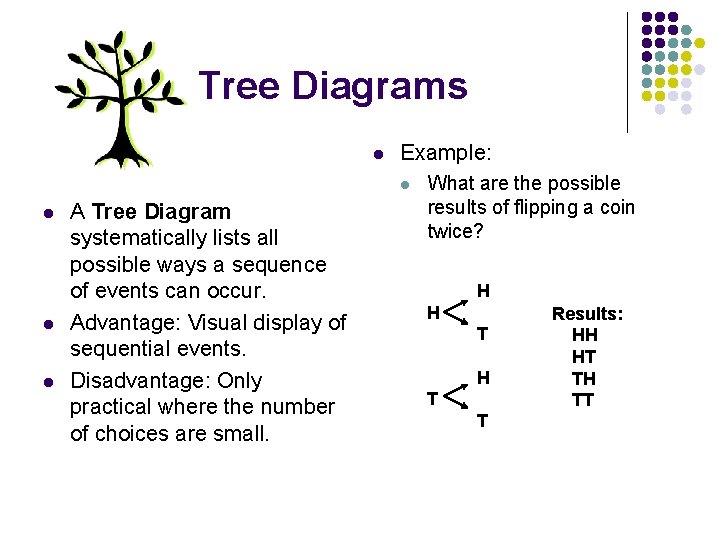
Tree Diagrams l Example: l l A Tree Diagram systematically lists all possible ways a sequence of events can occur. Advantage: Visual display of sequential events. Disadvantage: Only practical where the number of choices are small. What are the possible results of flipping a coin twice? H H T T Results: HH HT TH TT

Multiplication Rule (events independent) l In a sequence of n events in which the first event has k 1 possibilities, the second event k 2, etc. (to kn), the total number of possibilities is k 1* k 2* …* kn-1* kn. l Example 1: l l l What are the possible results of flipping a coin twice? Answer: 2 * 2 = 4 The Multiplication Rule replaces tree diagrams of any size. Consider the tree diagram that would result from the following example. l Example 2: l l What are the dinner possibilities if there are 10 beverages, 6 appetizers, 11 entrees, and 8 desserts? Answer: 10 * 6 * 11 * 8 = 5, 280 dinner possibilities.