Combinations and Probability Sample Space the set of

Combinations and Probability

Sample Space – the set of all possible outcomes • Flipping a coin • Rolling a die

Combination – When things are combined, how many possibilities are there when order is not important. • Flipping a coin and then rolling a die

U du - Find the number of possible combinations if you: • Flip a penny and a nickel (heads or tails) • Flip a penny and a nickel and roll a six sided die

1. The Warriors need to choose a point guard, shooting guard, and center to represent their team at the All Stars game. Here’s their current roster: Point Guard: Shaun Livingston, Stephen Curry, Quinn Cook Shooting Guard: Nick Young, Klay Thompson, Patrick Mc. Caw Center: David West, Jordan Bell, Damian Jones, Kevon Looney, Ja. Vale Mc. Gee, Zaza Pachulia a. How many possible combinations of representatives do they have?

Three coins are flipped, a nickle, a dime, and a quarter. What is the probability that the outcome shows exactly two heads Find the sample space Identify the number of favorable outcomes and the total number of outcome Use the Theoretical Probability formula

2. Based on the numbers above, the warriors have 3 point guards, 3 shooting guards, and 5 centers. What’s the probability that the coach picks a name at random and that person is: a. A point guard b. Not a center c. Steph or Klay D. Shaq

Independent vs Dependent events • Independent event – the occurrence of one event doesn't affect the occurrence of the other event • Dependent event -

Independent or Dependent 1. I will select one person in this class to be president, and a different person will be vice-president. 2. I will give a candy bar to anyone who gets #1 on the test right, and another candy bar to anyone who gets #2 right. 3. I will give a candy bar only to anyone who gets #1 and #2 right. 1. I pick someone to tell me their favorite sport, then I ask them pick their second favorite

Probability of Independent events • Two events A and B are independent if and only if the probability that both events occur is the product of the probabilities of the events • P(A and B)= P(A) * P(B) • Rolling a dice and flipping a coin. What is the probability of getting a heads and a 4.

A random fan gets picked from the audience. This fan has to pick a basketball at random of a bag of 3 red basketballs, 3 blue basketballs, and 3 gold basketballs. This fan randomly picks a basketball, puts the basketball back, and randomly picks again. If he picks a blue basketball first and a gold second, he wins $10, 000. What is the probability that the fan wins $10, 000?

Probability of Dependent Events • If two events, A and B, are dependent events, then the probability of both events occurring is the product of the probability of A and the conditional probability of B. • P(A and B)= P(A) * P(BIA) The probability of winning the Lotto is a conditional probability

A random fan gets picked from the audience. This fan has to pick a basketball at random of a bag of 3 red basketballs, 3 blue basketballs, and 3 gold basketballs. This fan randomly picks a basketball, doesn’t put the basketball back, and randomly picks again. If he picks a blue basketball first and a gold second, he wins $10, 000.

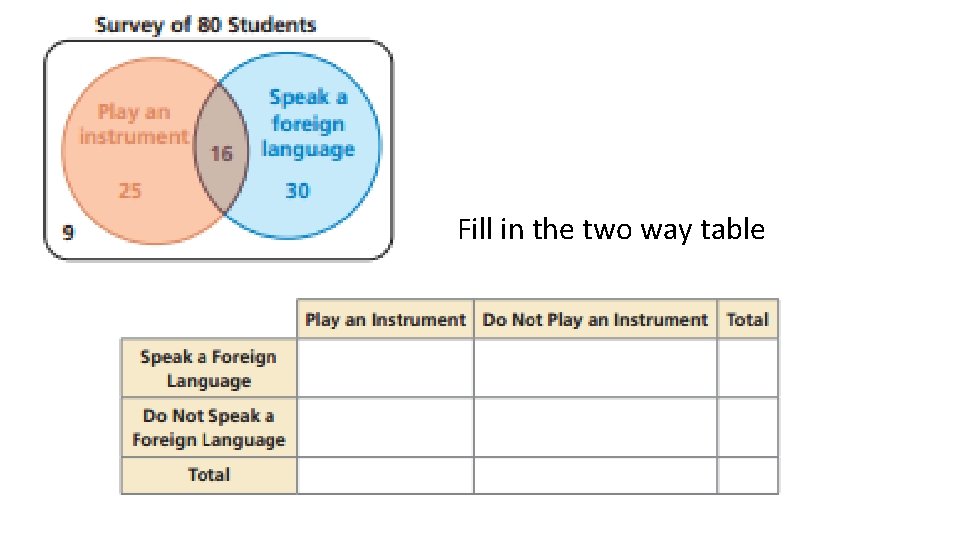
Fill in the two way table

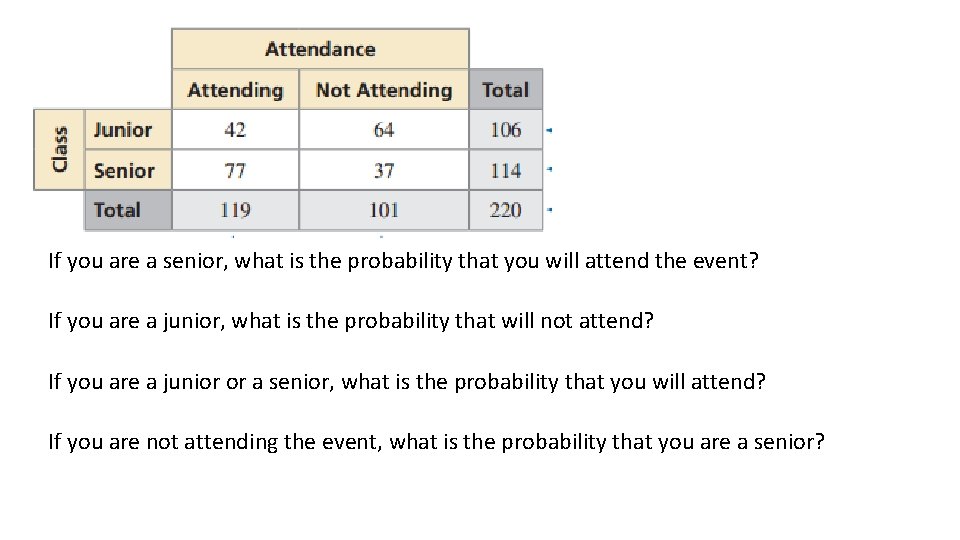
If you are a senior, what is the probability that you will attend the event? If you are a junior, what is the probability that will not attend? If you are a junior or a senior, what is the probability that you will attend? If you are not attending the event, what is the probability that you are a senior?

The Warriors’s Marketing Team need to know more about their fans. They decided to survey a small sample of them. They have set up this table to help organize their data: What’s the probability of the team randomly picking a fan who doesn’t live in the Bay Area? What’s the probability of the team randomly picking a fan who is over 30 years old? Is it more likely for a fan to be over 30 or under 30, given they live in the Bay Area? Is it more likely for a fan to live in the Bay or not, given they’re over 30?

Permutions – when the order matters, when change in order counts. • Iron Man, Cap, Hulk, Thor, Black Widow, and Hawkeye are having some coffee. Nick Fury calls, and wants one of them to be Chief, another to be Vice-Chief, and the third to be Secretary. How many ways could you pick heros at random to fill these roles?

Combination – a selection of objects in which order doesn’t matter. • Iron Man, Cap, Hulk, Thor, Black Widow, and Hawkeye are having some coffee. Nick Fury calls, and wants three of them to come by to take some promotional pictures. How many ways could you pick heros at random?