Combinational Logic Design Substractor Overview Binary Subtraction 2s

Combinational Logic Design: Substractor

Overview • Binary Subtraction – 2’’s complement – Extension to r’s complement – Subtraction with complements • Binary Adders/Subtractors – Signed numbers – Signed Addition/Subtraction – Overflow problem • Binary Multipliers Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 2

Binary Subtraction • Unsigned numbers: minus sign is not explicitly represented. • Given 2 binary numbers M and N, find M-N: – Case I: M ≥ N, thus, MSB of Borrow is 0 B 000110 M 11110 30 N -1 0 0 1 1 -19 Result is Correct Dif 0 1 1 11 – Case II: N > M, thus MSB of Borrow is 1 B 11 1000 M 1001 1 19 N -1 1 0 -30 Result requires correction! Dif 1 0 1 21 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 3

Binary Subtraction (cont. ) n • In general, if N > M, Dif = M-N+2 , where n = # bits. • In Case II of the previous example, Dif= 19 5 -30+2 = 21. • To correct the magnitude of Dif, which n n should be N-M, calculate 2 -(M-N+2 ). • This is known as the 2’’s complement of Dif. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 4

General Procedure • To subtract two n-bit numbers, M-N, in base 2: – Find M-N. – If MSB of Borrow is 0, then M ≥ N. Result is positive and correct. – If MSB of Borrow is 1, then N > M. Result is negative and its magnitude must be corrected n by subtracting it from 2 (find its 2’s complement). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 5

Another Subtraction Example • Given M = 01100100 and N = 10010110, find M-N. B 1 0011 1100 M 0110 0100 N -1 0 0 1 1 0 Dif 11001 110 n 10000 Dif - 1 1 0 0 1 1 1 0 0001 10010 2 Nov-0110 100 -50 206 256 -206 50 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 6

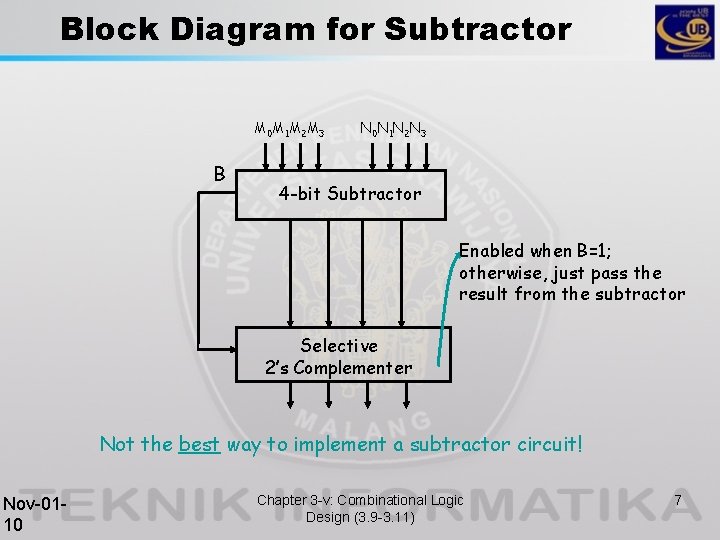
Block Diagram for Subtractor M 0 M 1 M 2 M 3 B N 0 N 1 N 2 N 3 4 -bit Subtractor Enabled when B=1; otherwise, just pass the result from the subtractor Selective 2’s Complementer Not the best way to implement a subtractor circuit! Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 7

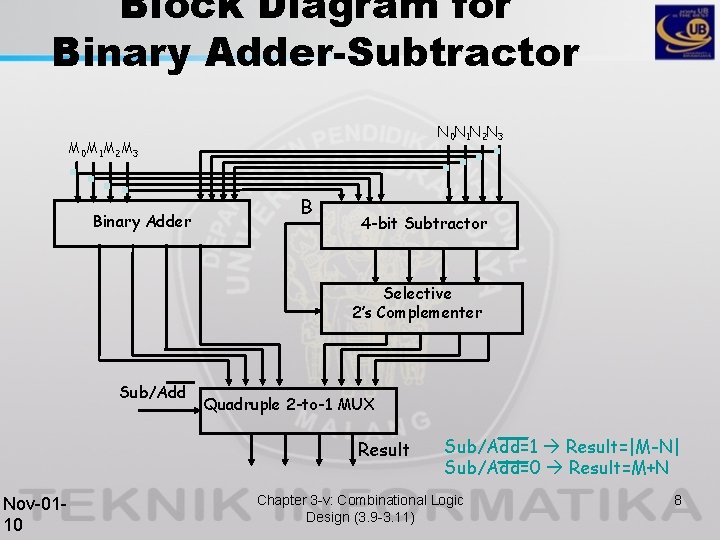
Block Diagram for Binary Adder-Subtractor N 0 N 1 N 2 N 3 M 0 M 1 M 2 M 3 Binary Adder B 4 -bit Subtractor Selective 2’s Complementer Sub/Add Quadruple 2 -to-1 MUX Result Nov-0110 Sub/Add=1 Result=|M-N| Sub/Add=0 Result=M+N Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 8

Complements • There are 2 types of complements for each base-r system: – Radix (r’s) complement, ex. 2’s complement and 10’s complement. – Diminished radix (r-1’s) complement, ex. 1’s complement and 9’s complement. • We examine only 2’s and 1’s complements for base 2. Same concepts hole for other bases (ex. decimal). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 9

2’s Complement • For a positive n digit number N 2 in binary, the 2's complement, 2 C(N 2), is given by: – 2 C(N 2) = { 2 n-N 2 , 0 , if n > 0 if n = 0 • Example: N 2 =1010 – 2 C(N 2) = 24 -N 2 = 100002 – 10102 = 01102 • Example: N 2 =11111 – 2 C(N 2) = 25 -N 2 = 1000002 – 111112 = 00001 2 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 10

2’s Complement (cont. ) • Here’s an easier way to compute the 2’s complement: 1. Leave all least significant 0’s and first 1 unchanged. 2. Replace 0 with 1 and 1 with 0 in all remaining higher significant bits. • Examples: complement unchanged – N = 1010 01 10 2’s complement Nov-0110 complement unchanged N = 01011000 10101000 2’s complement Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 11

1’s Complement • For a positive n digit number N 2 in binary, the 1's complement, 1 C(N 2), is given by: – 1 C(N 2) = (2 n-1) - N 2 • Example: N 2 =011 – 1 C(N 2) = (23 -1)-N 2 = 1112 – 0112 = 1002 • Example: N 2 =1010 – 1 C(N 2) = (24 -1) - N 2 = 11112 – 10102 = 0101 2 • Observation: 1’s complement can be derived by just complementing all the bits in the number. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 12

Observation • Compare 1’s complement with 2’s complement: – 2 n-N = [(2 n-1) - N] + 1 • Thus, the 2’s complement can be obtained by deriving the 1’s complement and adding 1 to it. • Example: – N = 1001 – 2 C(N) = 24 – N = 10000 – 1001 = 0111 – 1 C(N) = 24 – 1 - N = 1111 – 1001 = 0110 2 C(N) = 1 C(N) + 1 = 0110 + 0001 = 0111 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 13

Subtraction with Complements • To perform M-N = M+(-N), we may use a complement form to represent the negative number -N, and perform a “plain old addition”. • Need to be able to “convert” the result. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 14

Subtraction with 2’s complement • If we use 2's complements to represent negative numbers: n n 1. Form RI = M + 2 C(N 2) = M + (2 -N) = M – N + 2. • If there is a nonzero carry out of the addition, M ≥ N, so discard that carry and the remaining digits are the result R = M-N. 1. Otherwise, M < N, so take the 2’s complement of RI (=2 n- RI = 2 n- (M – N + 2 n) = N – M), and attach a minus sign in front, i. e. , the result R is -2 C([RI]2) = -(N-M). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 15

Example • A = 1010100 (8410), B = 1000011 (6710) • Find R = A-B: – 2 C(B) = 0111101 (6110) – A+2 C(B) = 1010100+0111101 = 10010001 – Discard carry, R = 0010001 (1710) ✔ • Find R = B-A: – 2 C(A) = 0101100 (4410) – B+2 C(A) = 1000011+0101100 = 1101111 – R = -2 C(B+A) = -0010001 (-17) ✔ Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 16

Subtraction with 1’s complement • If we use 1's complements to represent negative numbers: 1. Form RI = M + 1 C(N 2) = M + (2 n-1 -N) = M – N + 2 n-1. 2. If there is a nonzero carry out of the addition, M ≥ N, so discard that carry and add 1 to the remaining digits. The result R = M-N. 3. Otherwise, M <n. N, so take the 1’s complement of RI n n (=2 - 1 - RI = 2 - 1 - (M – N + 2 -1) = N – M ), and attach a minus sign in front, i. e. , the result R is -1 C([RI]2) = -(N-M). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 17

Example • A = 1010100 (8410), B = 1000011 (6710) • Find R = A-B: – 1 C(B) = 0111100 (6010) – A+B = 1010100+0111100 = 10010000 – Discard carry and add 1, R = 0010000 + 1 = 0010001 (1710) ✔ • Find R = B-A: – 1 C(A) = 0101011 – B+A = 1000011+0101011 = 1101110 – R = -1 C(B+A) = -0010001 (-17) ✔ Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 18

Binary Adder/Subtractors • If we perform subtraction using complements, we eliminate the subtraction operation, and thus, can use an adder with appropriate complementer for subtraction. • Actually, we can use an adder for both addition and subtraction: – Complement subtrahend for subtraction – Do not complement subtrahend for addition • Thus, to form an adder-subtractor circuit, we only need a selective complementer and an adder. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 19

Binary Adder/Subtractors (cont. ) • The subtraction A-B can be performed by taking the 2's complement of B and adding to A. • The 2's complement of B can be obtained by complementing B and adding one to the result. A-B = A + 2 C(B) = A + 1 C(B) + 1 = A + B’ + 1 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 20

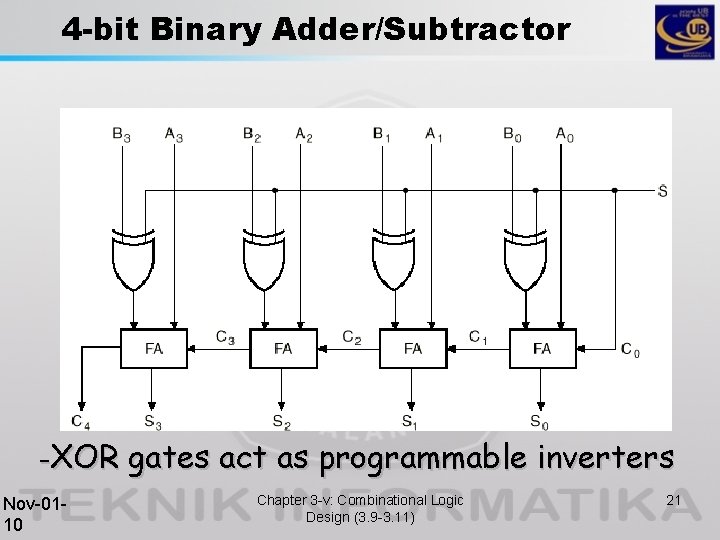
4 -bit Binary Adder/Subtractor –XOR Nov-0110 gates act as programmable inverters Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 21

4 -bit Binary Adder/Subtractor (cont. ) • When S=0, the circuit performs A + B. The carry in is 0, and the XOR gates simply pass B untouched. • When S=1, the carry into the least significant bit (LSB) is 1, and B is complemented (1’s complement) prior to the addition; hence, the circuit adds to A the 1’s complement of B plus 1 (from the carry into the LSB). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 22

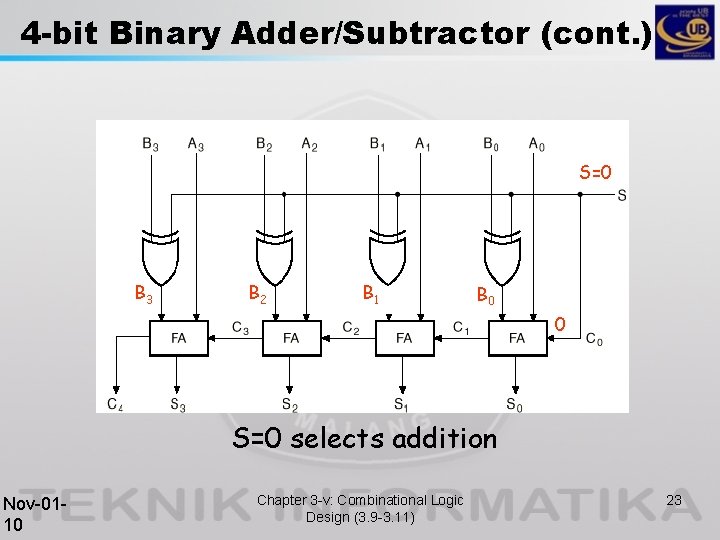
4 -bit Binary Adder/Subtractor (cont. ) S=0 B 3 B 2 B 1 B 0 0 S=0 selects addition Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 23

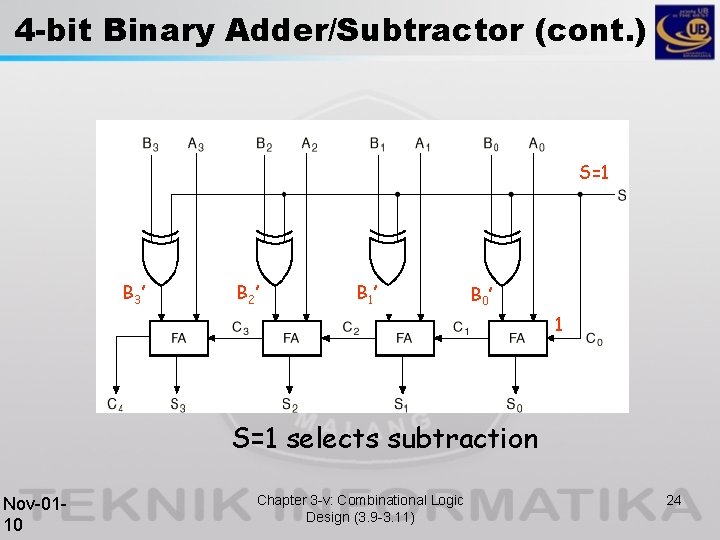
4 -bit Binary Adder/Subtractor (cont. ) S=1 B 3’ B 2’ B 1 ’ B 0’ 1 S=1 selects subtraction Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 24

4 -bit Binary Adder/Subtractor (cont. ) When C 4 = 0 and S=1 it means that A < B and we must correct the result R 3…R 0 (see slide 15). Thus, we must compute 2’s complement of R 3…R 0: Use a specialized 2’s complement circuit or Use the 4 -bit Adder/Subtractor again, with A 3…A 0=0000, B 3…B 0=R 3…R 0, and S=1. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 25

Signed Binary Numbers • Signed-magnitude system: Singed numbers are represented using the MSB of the binary number to indicate the number’s sign: – If MSB is 0 number is positive – If MSB is 1 number is negative • Do not confuse with unsigned numbers! Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 26

Signed Binary Numbers (cont. ) • For example: – -1010 is • -10102 in unsigned (- sign is implicit) • 110102 in singed (- sing is indicated in MSB=1) • Another example: – 10112 is • 1110 in unsigned • -310 in signed Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 27

Signed Binary Numbers (cont. ) • To implement signed-magnitude addition and subtraction we need to separate the sing bit from the magnitude bits, and treat the magnitude bits as an unsigned number (do correction whenever necessary). • To avoid correction, use the singedcomplement system. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 28

Signed-Complement System • The magnitude of the negative number is represented in a complement form (2’s or 1’s complement). • Ex. : Use 8 -bits to represent -910 and 910 – -910 is: • 10010012 in singed-magnitude • 111101102 in singed-1’s complement • 111101112 in singed-2’s complement – 910 is 000010012 in any of the above systems Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 29

Signed-Magnitude Addition-Subtraction • To perform addition or subtraction of two numbers M and N in signed-magnitude, follow ordinary arithmetic rules: – Same signs: Add and keep same sign. – Different signs: Subtract N from M; if end Borrow is 1, correct result by taking its 2’s complement. Sign is negative. – Example: M: 00011001, N: 10100101 N is negative, so find |M-N|=0011001 -0100101 =1110100, with end borrow 1. This implies that M-N is a negative number, so to correct find its 2’s complement 0001100. Result is 10001100. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 30

Signed-Complement Addition • “Addition of two signed numbers, with negative ones represented in signed-2’s complement, is obtained by adding the two numbers (including the sing bits). Carry out is discarded”. • Examples: (Assume 5 -bit representations) 01010 (+10) 10110 (-10) +00101 (+5) +11011 (-5) +00101 (+5) 01111 (+15) 00101 (+5) 11011 (-5) Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 10110 (-10) +11011 (-5) 10001 (-15) 31

Signed-Complement Addition (cont. ) • Do not get confused reading negative numbers in signed-2’s complement! Remember, if MSB is 1 the number is negative and you need to find the 2’s complement of the magnitude. • Example: What’s the decimal equivalent of 10010012? – Negative number, since MSB=1 – Magnitude = 001001 2’s complement of magnitude = 110111 – The number is -5510 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 32

Signed-Complement Subtraction • “Subtraction of two signed numbers, with negative ones represented in signed-2’s complement, is obtained by taking the 2’s complement of the subtrahend (including sing bit) and add it to the minuend. Discard carry out”. • Examples: (Assume 5 -bit representations) Nov-0110 01010 (+10) -00101 -(+5) 01010 (+10) 10110 (-10) -11011 -(-5) -00101 -(+5) -11011 -(-5) 01010 (+10) +11011 +(-5) 00101 (+5) 01010 (+10) +00101 +(+5) 01111 (+15) 10110 (-10) +11011 +(-5) 10001 (-15) Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 10110 (-10) +00101 +(+5) 11011 (-5) 33

The Overflow problem • If the sum of two n-bit numbers results in an n+1 number, then an overflow conditions is said to occur. • Detection of overflow can be implemented using either hardware or software. • Detection depends on number system used: signed or unsigned. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 34

The Overflow problem in Unsigned System • Addition: – When Carry out is 1. • Subtraction: – Can never occur. Magnitude of the result is always equal or smaller than the larger of the two numbers. • Not REALLY a problem! Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 35

The Overflow problem in Signed-2’s Complement • Remember that the MSB is the sign. But, the sign is also added! Thus, a carry out equal to 1 does not necessarily indicate overflow. • Overflow can occur ONLY when both numbers have the same sign. This condition can be detected when the carry out (Cn) is different than the carry at the previous position (Cn-1). Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 36

The Overflow problem in Signed-2’s Complement (cont. ) • Example 1: Let M=6510 and N=6510 in an 8 -bit signed-2’s complement system. – M = N = 010000012 – M+N = 10000010 with Cn=0. This is clearly wrong! Bring Cn as the MSB to get 0100000102 (13010) which is correct, but requires 9 -bits overflow occurs. • Example 2: Let M=-6510 and N=-6510 in an 8 -bit signed 2’s complement system. – M = N = 101111112 – M+N = 01111110 with Cn=1. This is wrong again! Bring Cn as the MSB to get 1011111102 (-13010) which is correct, but also requires 9 -bits overflow occurs. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 37

Overflow Detection in Signed-2’s Complement • Overflow conditions is detected by comparing the carry values into and out of the sign bit (Cn and Cn-1). n-bit Adder/Subtractor with Overflow Detection Logic V C Cn Cn+1 n-bit Adder/Subtractor • C =1 indicates overflow condition when adding/subtr. unsigned numbers. • V=1 indicates overflow condition when adding/subtr. signed-2’s complement numbers Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 38

Binary Multiplier • Binary multiplication resembles decimal multiplication: – n-bit multiplicand is multiplied by each bit of the m-bit multiplier, starting from LSB, to form n partial products. – Each successive set of partial products is shifted 1 bit to the left. – Derive result by addition the m rows of partial products. Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 39

Binary Multiplier (cont. ) • Example: – Multiplier A=A 1 A 0 and multiplicand B=B 1 B 0 – Find C = Ax. B: B 1 x A 1 B 0 A 0 --------A 0 B 1 A 0 B 0 + A 1 B 1 A 1 B 0 C C 2 C 0 ---------------3 Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 40

Binary Multiplier Circuit 2 -bit by 2 -bit multiplier Half Adders are Sufficient since there is no Carry-in in addition to the two inputs to sum Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 41

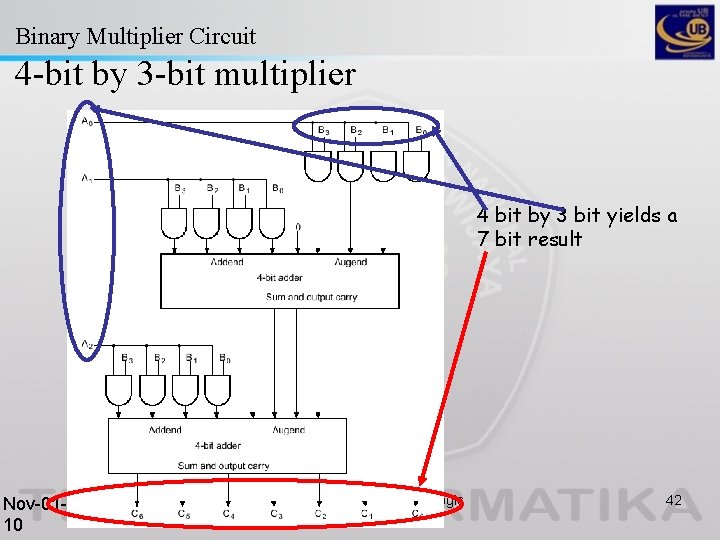
Binary Multiplier Circuit 4 -bit by 3 -bit multiplier 4 bit by 3 bit yields a 7 bit result Nov-0110 Chapter 3 -v: Combinational Logic Design (3. 9 -3. 11) 42