Combinational Logic Design Case Studies z General design

Combinational Logic Design Case Studies z General design procedure z Examples y Calendar subsystem y BCD to 7 -segment display controller y Process line controller y Logical function unit z Arithmetic y Integer representations y Addition/subtraction y Arithmetic/logic units CS 150 - Spring 2001 - Combinational Examples - 1

General Design Procedure for Combinational Logic z 1. Understand the Problem y What is the circuit supposed to do? y Write down inputs (data, control) and outputs y Draw block diagram or other picture z 2. Formulate the Problem using a Suitable Design Representation y Truth table or waveform diagram are typical y May require encoding of symbolic inputs and outputs z 3. Choose Implementation Target y ROM, PAL, PLA y Mux, decoder and OR-gate y Discrete gates z 4. Follow Implementation Procedure y K-maps for two-level, multi-level y Design tools and hardware description language (e. g. , Verilog) CS 150 - Spring 2001 - Combinational Examples - 2

Calendar Subsystem z Determine number of days in a month (to control watch display) y Used in controlling the display of a wrist-watch LCD screen y Inputs: month, leap year flag y Outputs: number of days z Use software implementation to help understand the problem integer number_of_days ( month, leap_year_flag) { switch (month) { case 1: return (31); case 2: if (leap_year_flag == 1) then return (29) else return (28); case 3: return (31); case 4: return (30); case 5: return (31); case 6: return (30); case 7: return (31); case 8: return (31); case 9: return (30); case 10: return (31); case 11: return (30); case 12: return (31); default: return (0); } } CS 150 - Spring 2001 - Combinational Examples - 3
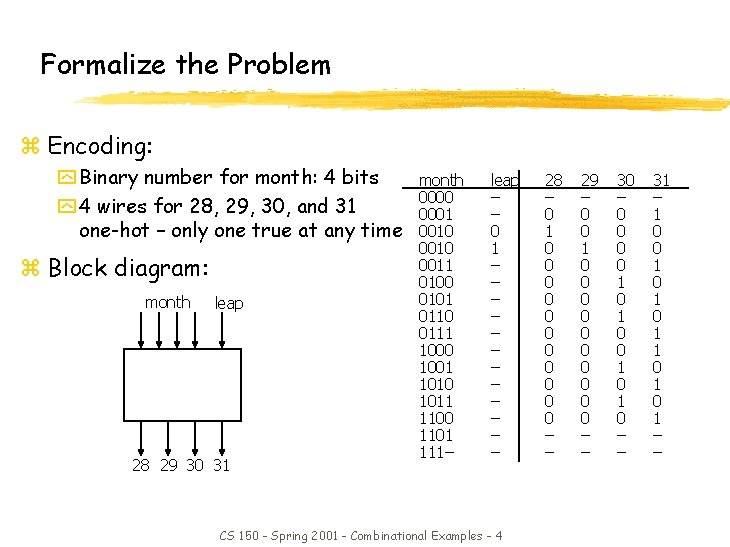
Formalize the Problem z Encoding: y Binary number for month: 4 bits y 4 wires for 28, 29, 30, and 31 one-hot – only one true at any time z Block diagram: month leap 28 29 30 31 month 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 111– leap – – 0 1 – – – CS 150 - Spring 2001 - Combinational Examples - 4 28 – 0 1 0 0 0 – – 29 – 0 0 1 0 0 0 0 0 – – 30 – 0 0 1 0 – – 31 – 1 0 0 1 0 1 – –
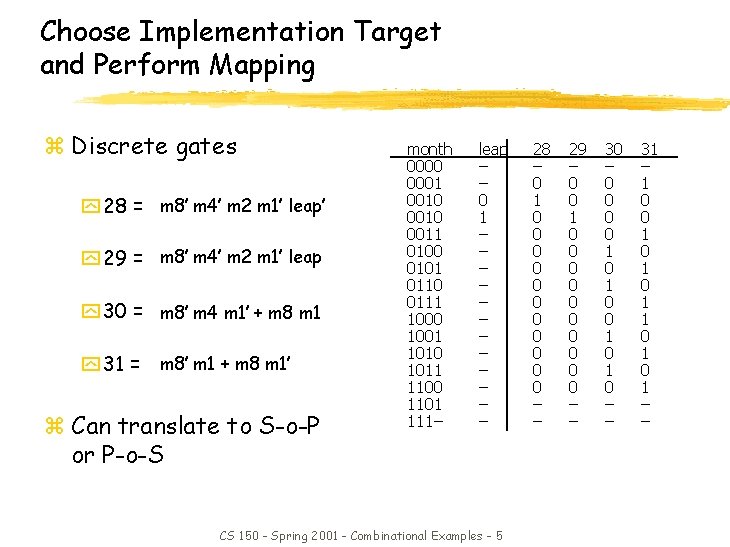
Choose Implementation Target and Perform Mapping z Discrete gates y 28 = m 8’ m 4’ m 2 m 1’ leap’ y 29 = m 8’ m 4’ m 2 m 1’ leap y 30 = m 8’ m 4 m 1’ + m 8 m 1 y 31 = m 8’ m 1 + m 8 m 1’ z Can translate to S-o-P or P-o-S month 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 111– leap – – 0 1 – – – CS 150 - Spring 2001 - Combinational Examples - 5 28 – 0 1 0 0 0 – – 29 – 0 0 1 0 0 0 0 0 – – 30 – 0 0 1 0 – – 31 – 1 0 0 1 0 1 – –
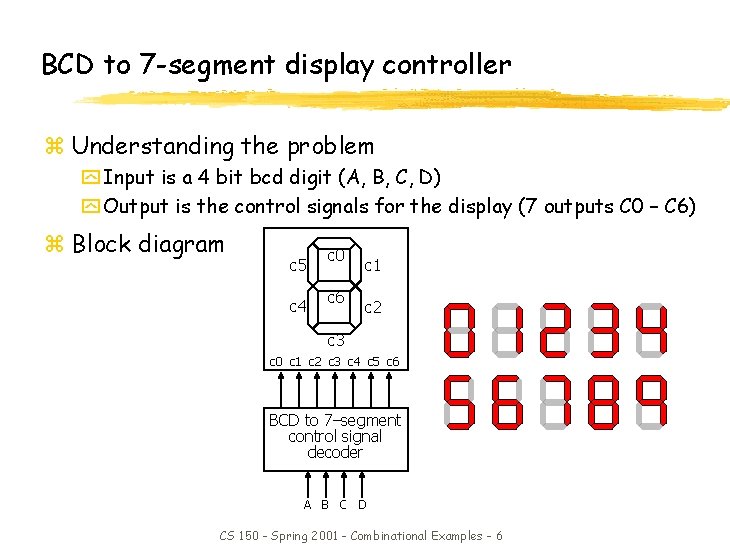
BCD to 7 -segment display controller z Understanding the problem y Input is a 4 bit bcd digit (A, B, C, D) y Output is the control signals for the display (7 outputs C 0 – C 6) z Block diagram c 5 c 4 c 0 c 6 c 1 c 2 c 3 c 0 c 1 c 2 c 3 c 4 c 5 c 6 BCD to 7–segment control signal decoder A B C D CS 150 - Spring 2001 - Combinational Examples - 6
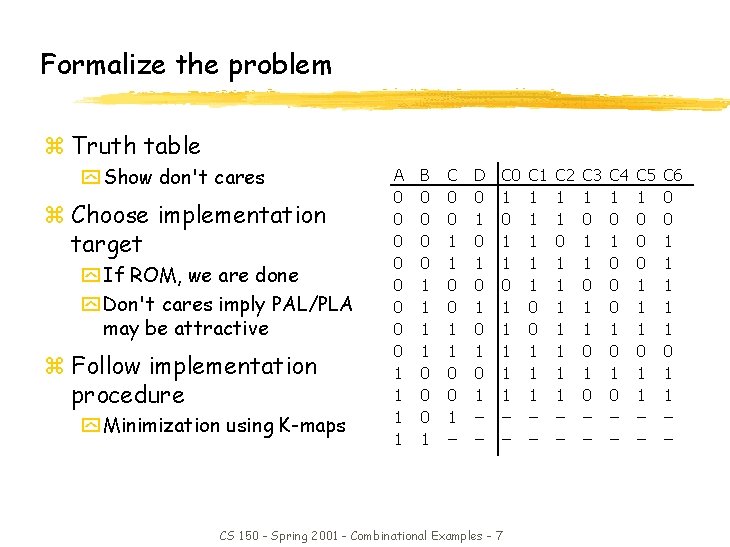
Formalize the problem z Truth table y Show don't cares z Choose implementation target y If ROM, we are done y Don't cares imply PAL/PLA may be attractive z Follow implementation procedure y Minimization using K-maps A 0 0 0 0 1 1 B 0 0 1 1 0 0 0 1 C 0 0 1 1 0 0 1 – D 0 1 0 1 0 1 – – C 0 1 1 1 – – CS 150 - Spring 2001 - Combinational Examples - 7 C 1 1 1 0 0 1 1 1 – – C 2 1 1 0 1 1 1 1 – – C 3 1 0 1 1 0 – – C 4 1 0 0 0 1 0 – – C 5 1 0 0 0 1 1 1 0 1 1 – – C 6 0 0 1 1 1 0 1 1 – –
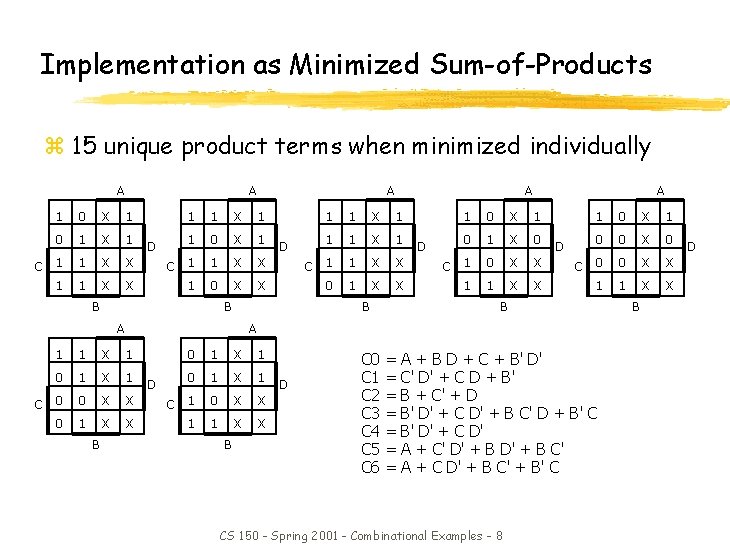
Implementation as Minimized Sum-of-Products z 15 unique product terms when minimized individually A A 1 0 X 1 0 1 X 1 C 1 1 X 1 1 0 X 1 X C 1 1 X X 1 0 X D B A 1 1 X 1 X C 1 1 X X 0 1 X D B A 1 0 X 1 0 1 X 0 X C 1 0 X X 1 1 X B A D 1 0 X 1 0 0 X C 0 0 X X X 1 1 X X D B A 1 1 X 1 0 1 X 1 C 0 0 X 0 1 X B A 0 1 X 1 X C 1 0 X X X 1 1 X X D B D C 0 C 1 C 2 C 3 C 4 C 5 C 6 = = = = A + B D + C + B' D' C' D' + C D + B' B + C' + D B' D' + C D' + B C' D + B' C B' D' + C D' A + C' D' + B C' A + C D' + B C' + B' C CS 150 - Spring 2001 - Combinational Examples - 8 B D
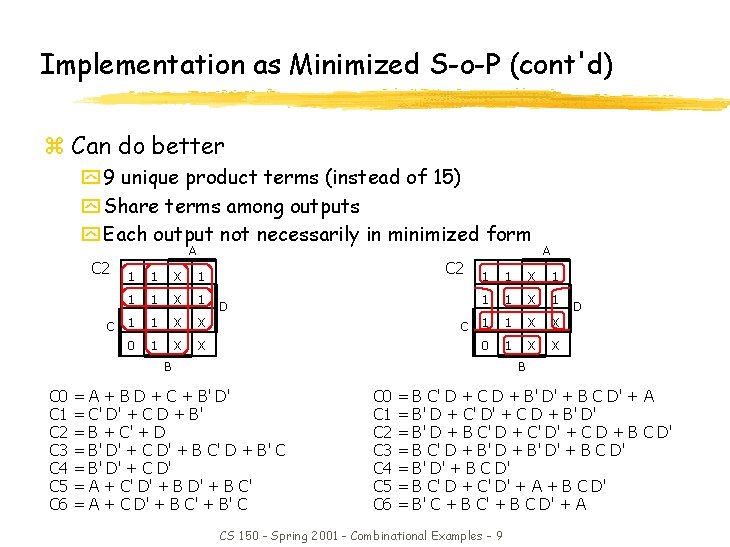
Implementation as Minimized S-o-P (cont'd) z Can do better y 9 unique product terms (instead of 15) y Share terms among outputs y Each output not necessarily in minimized form A C 2 1 1 X 1 C 1 1 X 0 1 X C 2 1 1 X 1 X C 1 1 X X X 0 1 X X D B C 0 C 1 C 2 C 3 C 4 C 5 C 6 = = = = A D B A + B D + C + B' D' C' D' + C D + B' B + C' + D B' D' + C D' + B C' D + B' C B' D' + C D' A + C' D' + B C' A + C D' + B C' + B' C C 0 C 1 C 2 C 3 C 4 C 5 C 6 = = = = B C' D + C D + B' D' + B C D' + A B' D + C' D' + C D + B' D' B' D + B C' D + C' D' + C D + B C D' B C' D + B' D' + B C D' B C' D + C' D' + A + B C D' B' C + B C' + B C D' + A CS 150 - Spring 2001 - Combinational Examples - 9
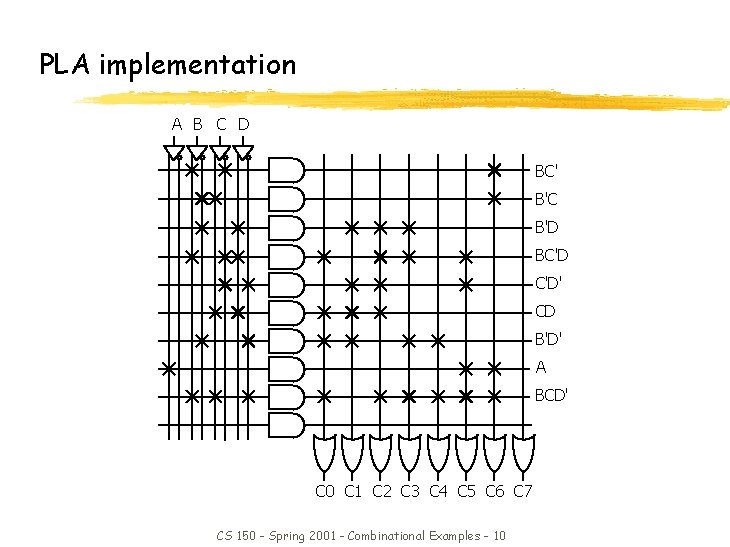
PLA implementation A B C D BC' B'C B'D BC'D C'D' CD B'D' A BCD' C 0 C 1 C 2 C 3 C 4 C 5 C 6 C 7 CS 150 - Spring 2001 - Combinational Examples - 10

PAL Implementation z Limit of 4 Product Terms per Output y Decomposition of functions with larger number of terms y Do not share terms in PAL anyway (although there are some with some shared terms) C 2 = B + C' + D C 2 = B' D + B C' D + C' D' + C D + B C D' C 2 = B' D + B C' D + C' D' + W W = C D + B C D' need another input and another output y Decompose into multi-level logic (hopefully with CAD support) x. Find common sub-expressions among functions C 0 C 1 C 2 C 3 C 4 C 5 C 6 = = = = C 3 + A' B X' + A D Y Y + A' C 5' + C' D' C 6 C 5 + A' B' D + A' C D C 4 + B D C 5 + A' B' X' D' Y + A' C D' C' C 4 + A Y + A' B X A C 4 + C C 5 + C 4' C 5 + A' B' C X = C' + D' Y = B' C' CS 150 - Spring 2001 - Combinational Examples - 11

Production Line Control z Rods of varying length (+/-10%) travel on conveyor belt y Mechanical arm pushes rods within spec (+/-5%) to one side y Second arm pushes rods too long to other side y Rods that are too short stay on belt y 3 light barriers (light source + photocell) as sensors y Design combinational logic to activate the arms z Understanding the problem y Inputs are three sensors y Outputs are two arm control signals y Assume sensor reads "1" when tripped, "0" otherwise y Call sensors A, B, C CS 150 - Spring 2001 - Combinational Examples - 12
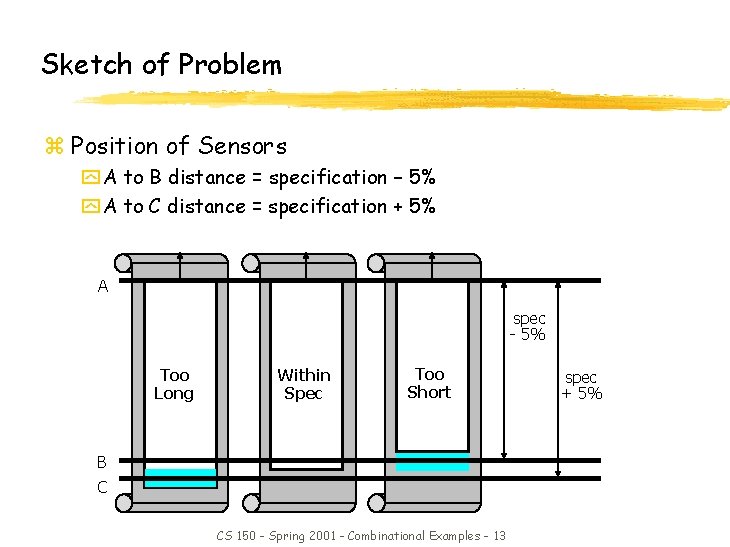
Sketch of Problem z Position of Sensors y A to B distance = specification – 5% y A to C distance = specification + 5% A spec - 5% Too Long Within Spec Too Short B C CS 150 - Spring 2001 - Combinational Examples - 13 spec + 5%
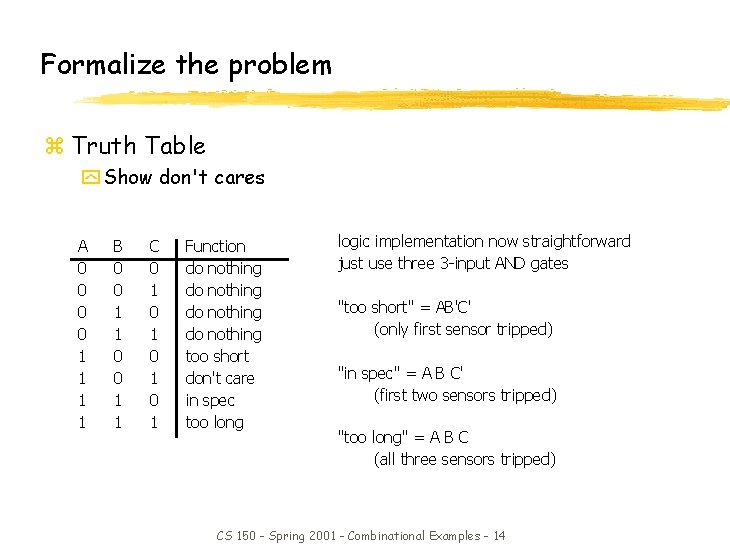
Formalize the problem z Truth Table y Show don't cares A 0 0 1 1 B 0 0 1 1 C 0 1 0 1 Function do nothing too short don't care in spec too long logic implementation now straightforward just use three 3 -input AND gates "too short" = AB'C' (only first sensor tripped) "in spec" = A B C' (first two sensors tripped) "too long" = A B C (all three sensors tripped) CS 150 - Spring 2001 - Combinational Examples - 14

Logical Function Unit z Multi-purpose Function Block y 3 control inputs to specify operation to perform on operands y 2 data inputs for operands y 1 output of the same bit-width as operands C 0 0 0 1 1 C 1 0 0 1 1 C 2 0 1 0 1 Function 1 A+B (A • B)' A xor B A xnor B A • B (A + B)' 0 Comments always 1 logical OR logical NAND logical xor logical xnor logical AND logical NOR always 0 3 control inputs: C 0, C 1, C 2 2 data inputs: A, B 1 output: F CS 150 - Spring 2001 - Combinational Examples - 15
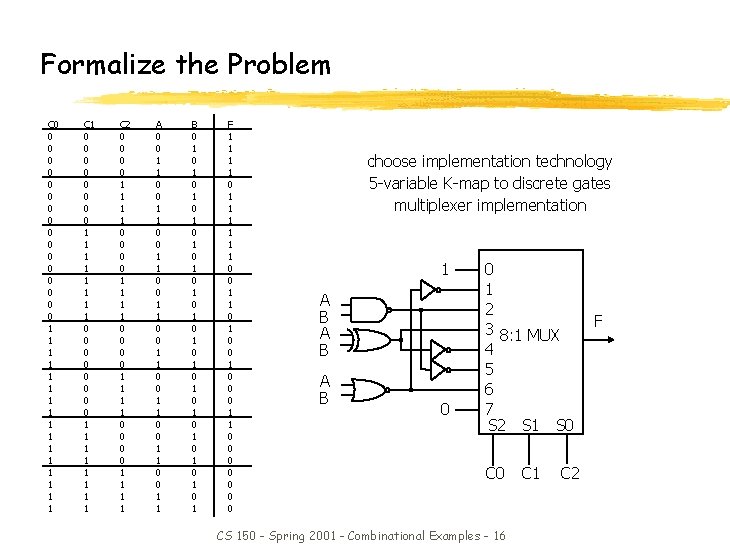
Formalize the Problem C 0 0 0 0 0 1 1 1 1 C 1 0 0 0 0 1 1 1 1 C 2 0 0 0 0 1 1 1 1 A 0 0 1 1 0 0 1 1 B 0 1 0 1 0 1 0 1 F 1 1 0 1 1 1 0 0 1 0 0 0 1 1 0 0 0 0 choose implementation technology 5 -variable K-map to discrete gates multiplexer implementation 1 A B A B 0 0 1 2 3 8: 1 MUX 4 5 6 7 S 2 S 1 S 0 CS 150 - Spring 2001 - Combinational Examples - 16 C 1 C 2 F

Arithmetic Circuits z Excellent Examples of Combinational Logic Design z Time vs. Space Trade-offs y Doing things fast may require more logic and thus more space y Example: carry lookahead logic z Arithmetic and Logic Units y General-purpose building blocks y Critical components of processor datapaths y Used within most computer instructions CS 150 - Spring 2001 - Combinational Examples - 17

Number Systems z Representation of positive numbers is the same in most systems z Major differences are in how negative numbers are represented z Representation of negative numbers come in three major schemes y Sign and magnitude y 1 s complement y 2 s complement z Assumptions y We'll assume a 4 bit machine word y 16 different values can be represented y Roughly half are positive, half are negative CS 150 - Spring 2001 - Combinational Examples - 18

Sign and Magnitude z One bit dedicate to sign (positive or negative) 0 100 = + 4 y sign: 0 = positive (or zero), 1 = negative 1 100 = – 4 z Rest represent the absolute value or magnitude y three low order bits: 0 (000) thru 7 (111) z Range for n bits y +/– 2 n– 1 (two representations for 0) z Cumbersome addition/subtraction y must compare magnitudes to determine sign of result – 7 – 6 – 5 +0 +1 1111 0000 1110 0001 1101 0010 +2 – 4 1100 0011 +3 – 3 1011 0100 +4 0101 +5 – 2 1010 1001 0110 +6 – 1 1000 0111 – 0 +7 CS 150 - Spring 2001 - Combinational Examples - 19

1 s Complement z If N is a positive number, then the negative of N ( its 1 s complement or N' ) is N' = (2 n– 1) – N y Example: 1 s complement of 7 2 1 4 4 2 – 1 7 = 10000 = 00001 = 1111 = 0111 1000 = – 7 in 1 s complement form y Shortcut: simply compute bit-wise complement ( 0111 -> 1000 ) CS 150 - Spring 2001 - Combinational Examples - 20

1 s complement (cont'd) z Subtraction implemented by 1 s complement and then addition z Two representations of 0 y Causes some complexities in addition z High-order bit can act as sign bit – 0 – 1 – 2 +0 +1 1111 0000 1110 0001 1101 – 3 0 100 = + 4 1 011 = – 4 – 5 0010 +2 1100 0011 +3 1011 0100 +4 1010 0101 1001 0110 1000 0111 +6 – 7 CS 150 - Spring 2001 - Combinational Examples - 21 +7 +5

2 s Complement z 1 s complement with negative numbers shifted one position clockwise y Only one representation for 0 y One more negative number than positive number – 1 y High-order bit can act as sign bit – 2 – 3 0 100 = + 4 1 100 = – 4 +0 1111 0000 1110 0001 1101 – 4 – 5 – 6 +1 0010 +2 1100 0011 +3 1011 0100 +4 1010 0101 1001 0110 1000 0111 +6 – 7 – 8 CS 150 - Spring 2001 - Combinational Examples - 22 +7 +5

2 s complement (cont’d) z If N is a positive number, then the negative of N ( its 2 s complement or N* ) is N* = 2 n – N y Example: 2 s complement of 7 2 subtract 4 7 = 10000 = 0111 1001 = repr. of – 7 y Example: 2 s complement of – 7 2 subtract 4 = 10000 – 7 = 1001 0111 = repr. of 7 y Shortcut: 2 s complement = bit-wise complement + 1 x 0111 -> 1000 + 1 -> 1001 (representation of -7) x 1001 -> 0110 + 1 -> 0111 (representation of 7) CS 150 - Spring 2001 - Combinational Examples - 23

2 s Complement Addition and Subtraction z Simple Addition and Subtraction y Simple scheme makes 2 s complement the virtually unanimous choice for integer number systems in computers 4 0100 – 4 1100 +3 0011 + (– 3) 1101 7 0111 – 7 11001 4 0100 – 4 1100 – 3 1101 +3 0011 1 10001 – 1 1111 CS 150 - Spring 2001 - Combinational Examples - 24

Why Can the Carry-out be Ignored? z Can't ignore it completely y Needed to check for overflow (see next two slides) z When there is no overflow, carry-out may be true but can be ignored – M + N when N > M: M* + N = (2 n – M) + N = 2 n + (N – M) ignoring carry-out is just like subtracting 2 n – M + – N where N + M 2 n– 1 (– M) + (– N) = M* + N* = (2 n– M) + (2 n– N) = 2 n – (M + N) + 2 n ignoring the carry, it is just the 2 s complement representation for – (M + N) CS 150 - Spring 2001 - Combinational Examples - 25
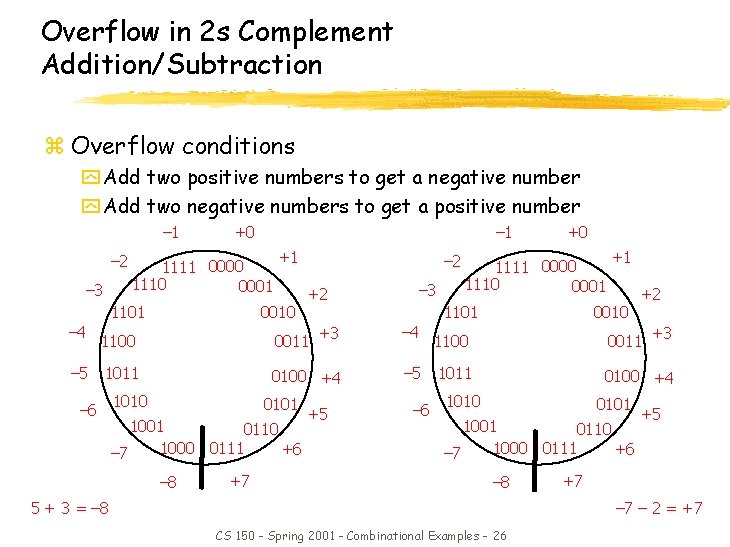
Overflow in 2 s Complement Addition/Subtraction z Overflow conditions y Add two positive numbers to get a negative number y Add two negative numbers to get a positive number – 1 – 2 – 3 +0 1111 0000 1110 0001 1101 – 4 – 5 – 1 +1 0010 – 2 +2 – 3 0011 +3 – 4 1011 0100 +4 – 5 1010 0101 1001 0110 1000 0111 +6 – 7 – 8 +7 +5 1111 0000 1110 0001 1100 – 6 +1 0010 +2 1100 0011 +3 1011 0100 +4 1010 0101 1001 0110 1000 0111 +6 – 7 – 8 5 + 3 = – 8 +5 +7 – 2 = +7 CS 150 - Spring 2001 - Combinational Examples - 26

Overflow Conditions z Overflow when carry into sign bit position is not equal to carry-out 0 1 1 1 5 3 – 8 0101 0011 1000 overflow 1 0 0 0 – 7 – 2 7 no overflow 10111 overflow 0 0 5 1001 1110 0101 0010 0111 1 1 – 3 – 5 – 8 no overflow CS 150 - Spring 2001 - Combinational Examples - 27 1101 1011 11000

Circuits for Binary Addition z Half adder (add 2 1 -bit numbers) y Sum = Ai' Bi + Ai Bi' = Ai xor Bi y Cout = Ai Bi z Full adder (carry-in to cascade for multi-bit adders) y Sum = Ci xor A xor B y Cout = B Ci + A B = Ci (A + B) + A B Ai 0 0 1 1 Bi 0 1 Sum 0 1 1 1 Cout 0 0 0 1 Ai 0 0 1 1 Bi 0 0 1 1 CS 150 - Spring 2001 - Combinational Examples - 28 Cin 0 1 0 1 Sum 0 1 1 0 0 1 Cout 0 0 0 1 1 1
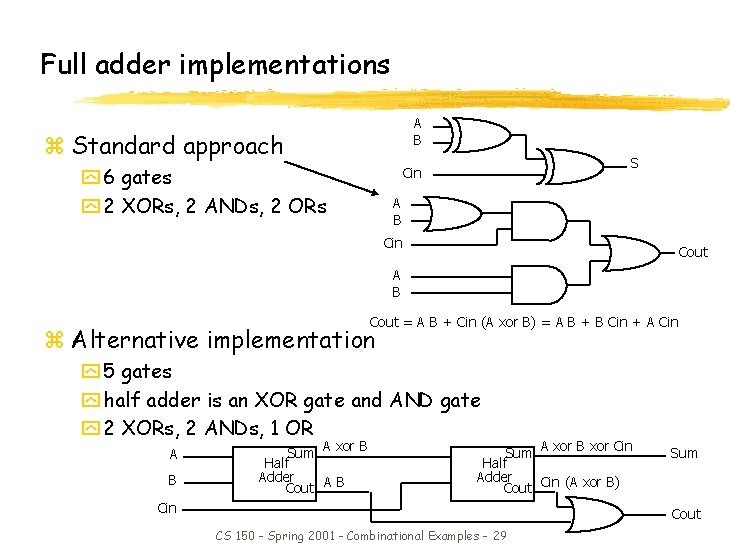
Full adder implementations A B z Standard approach y 6 gates y 2 XORs, 2 ANDs, 2 ORs S Cin A B Cin Cout A B Cout = A B + Cin (A xor B) = A B + B Cin + A Cin z Alternative implementation y 5 gates y half adder is an XOR gate and AND gate y 2 XORs, 2 ANDs, 1 OR A B Sum A xor B Half Adder Cout A B Sum A xor B xor Cin Half Adder Cout Cin (A xor B) Cin Sum Cout CS 150 - Spring 2001 - Combinational Examples - 29
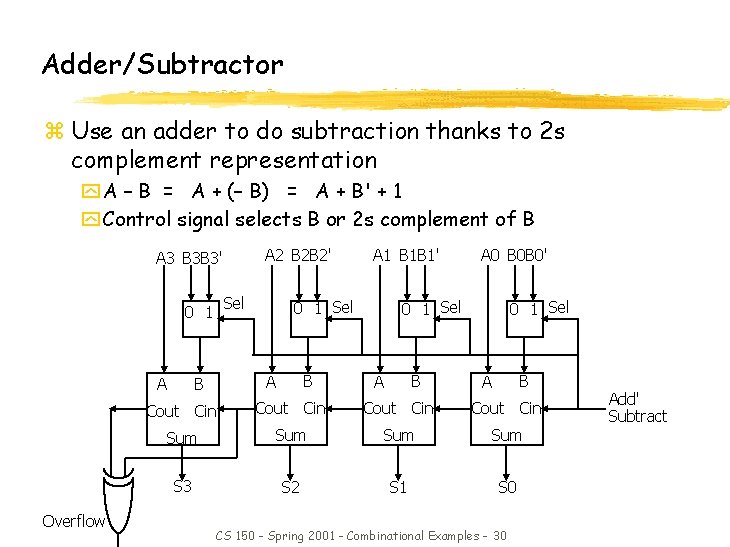
Adder/Subtractor z Use an adder to do subtraction thanks to 2 s complement representation y A – B = A + (– B) = A + B' + 1 y Control signal selects B or 2 s complement of B A 2 B 2 B 2' A 3 B 3 B 3' Sel 0 1 A Overflow 0 1 Sel B A 1 B 1 B 1' A 0 B 0 B 0' 0 1 Sel B A Cout Cin Sum Sum S 3 S 2 S 1 S 0 CS 150 - Spring 2001 - Combinational Examples - 30 Add' Subtract
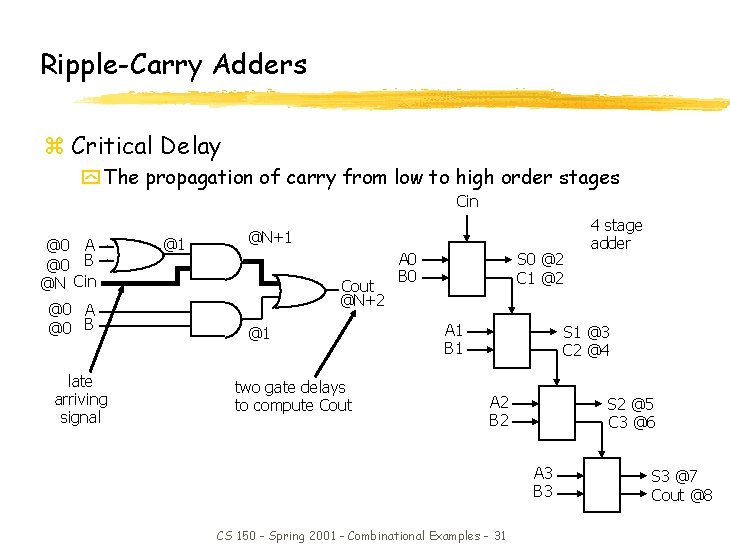
Ripple-Carry Adders z Critical Delay y The propagation of carry from low to high order stages Cin @0 A @0 B @N Cin @0 A @0 B late arriving signal @1 @N+1 Cout @N+2 @1 two gate delays to compute Cout A 0 B 0 S 0 @2 C 1 @2 A 1 B 1 4 stage adder S 1 @3 C 2 @4 A 2 B 2 S 2 @5 C 3 @6 A 3 B 3 CS 150 - Spring 2001 - Combinational Examples - 31 S 3 @7 Cout @8
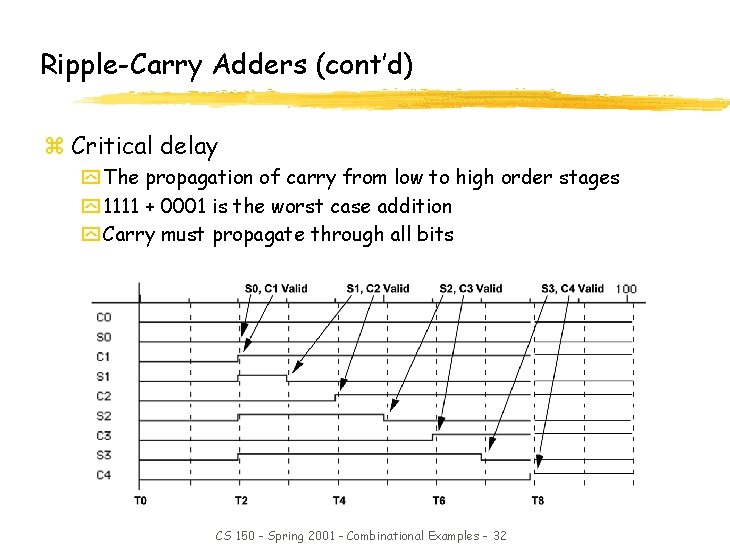
Ripple-Carry Adders (cont’d) z Critical delay y The propagation of carry from low to high order stages y 1111 + 0001 is the worst case addition y Carry must propagate through all bits CS 150 - Spring 2001 - Combinational Examples - 32

Carry-Lookahead Logic z Carry generate: Gi = Ai Bi y. Must generate carry when A = B = 1 z Carry propagate: Pi = Ai xor Bi y. Carry-in will equal carry-out here z Sum and Cout can be re-expressed in terms of generate/propagate: y. Si = Ai xor Bi xor Ci = Pi xor Ci y. Ci+1 = Ai Bi + Ai Ci + Bi Ci = Ai Bi + Ci (Ai + Bi) = Ai Bi + Ci (Ai xor Bi) = Gi + Ci Pi CS 150 - Spring 2001 - Combinational Examples - 33

Carry-Lookahead Logic (cont’d) z Re-express the carry logic as follows: y C 1 = G 0 + P 0 C 0 y C 2 = G 1 + P 1 C 1 = G 1 + P 1 G 0 + P 1 P 0 C 0 y C 3 = G 2 + P 2 C 2 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 C 0 y C 4 = G 3 + P 3 C 3 = G 3 + P 3 G 2 + P 3 P 2 G 1 + P 3 P 2 P 1 G 0 + P 3 P 2 P 1 P 0 C 0 z Each of the carry equations can be implemented with two-level logic y All inputs are now directly derived from data inputs and not from intermediate carries y this allows computation of all sum outputs to proceed in parallel CS 150 - Spring 2001 - Combinational Examples - 34
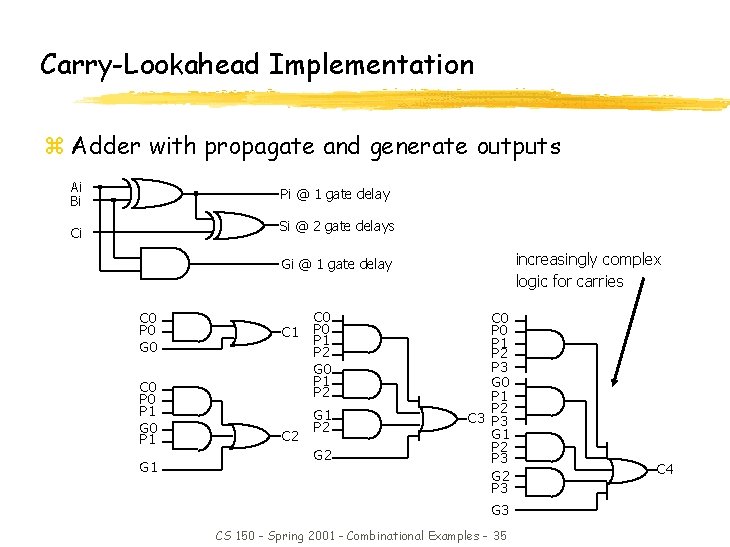
Carry-Lookahead Implementation z Adder with propagate and generate outputs Ai Bi Pi @ 1 gate delay Ci Si @ 2 gate delays increasingly complex logic for carries Gi @ 1 gate delay C 0 P 0 G 0 C 0 P 1 G 1 C 2 C 0 P 1 P 2 G 2 C 0 P 1 P 2 P 3 G 0 P 1 P 2 C 3 P 3 G 1 P 2 P 3 G 3 CS 150 - Spring 2001 - Combinational Examples - 35 C 4
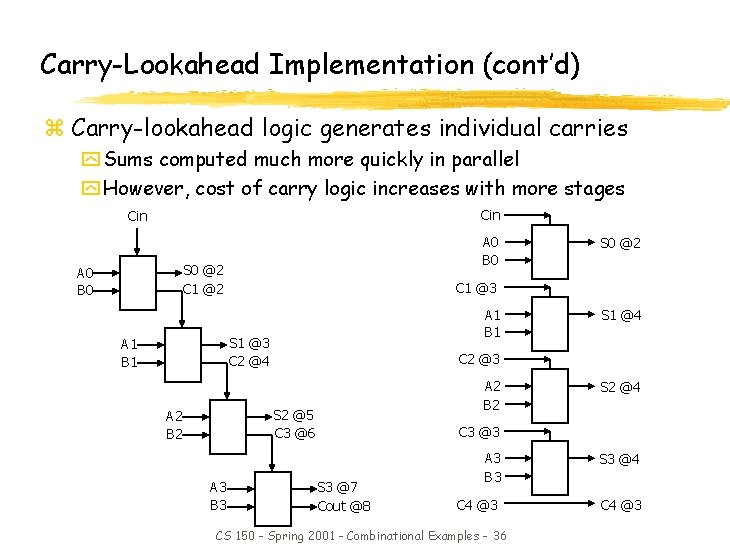
Carry-Lookahead Implementation (cont’d) z Carry-lookahead logic generates individual carries y Sums computed much more quickly in parallel y However, cost of carry logic increases with more stages Cin A 0 B 0 S 0 @2 C 1 @2 A 0 B 0 C 1 @3 A 1 B 1 S 1 @3 C 2 @4 A 1 B 1 A 3 B 3 S 1 @4 C 2 @3 A 2 B 2 S 2 @5 C 3 @6 A 2 B 2 S 0 @2 S 2 @4 C 3 @3 S 3 @7 Cout @8 A 3 B 3 S 3 @4 C 4 @3 CS 150 - Spring 2001 - Combinational Examples - 36
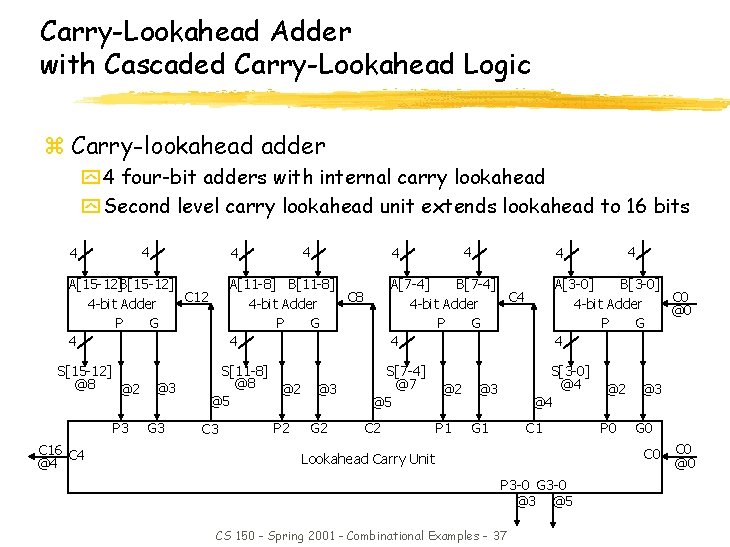
Carry-Lookahead Adder with Cascaded Carry-Lookahead Logic z Carry-lookahead adder y 4 four-bit adders with internal carry lookahead y Second level carry lookahead unit extends lookahead to 16 bits 4 4 A[15 -12]B[15 -12] C 12 4 -bit Adder P G 4 S[15 -12] @8 @2 P 3 C 16 C 4 @4 4 4 @3 G 3 A[11 -8] B[11 -8] C 8 4 -bit Adder P G 4 S[11 -8] @8 @2 @5 C 3 P 2 4 4 @3 G 2 A[7 -4] B[7 -4] C 4 4 -bit Adder P G 4 S[7 -4] @7 @5 C 2 @2 P 1 4 4 A[3 -0] B[3 -0] C 0 4 -bit Adder @0 P G 4 S[3 -0] @4 @4 @3 G 1 C 1 @2 P 0 @3 G 0 C 0 Lookahead Carry Unit P 3 -0 G 3 -0 @3 @5 CS 150 - Spring 2001 - Combinational Examples - 37 C 0 @0
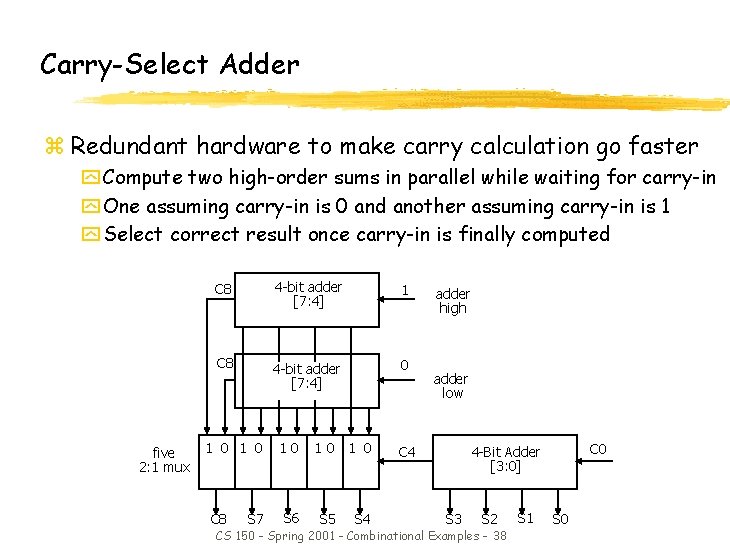
Carry-Select Adder z Redundant hardware to make carry calculation go faster y Compute two high-order sums in parallel while waiting for carry-in y One assuming carry-in is 0 and another assuming carry-in is 1 y Select correct result once carry-in is finally computed five 2: 1 mux C 8 4 -bit adder [7: 4] 1 C 8 4 -bit adder [7: 4] 0 1 0 C 8 S 7 10 S 6 1 0 S 5 S 4 adder high adder low C 4 C 0 4 -Bit Adder [3: 0] S 3 S 2 CS 150 - Spring 2001 - Combinational Examples - 38 S 1 S 0
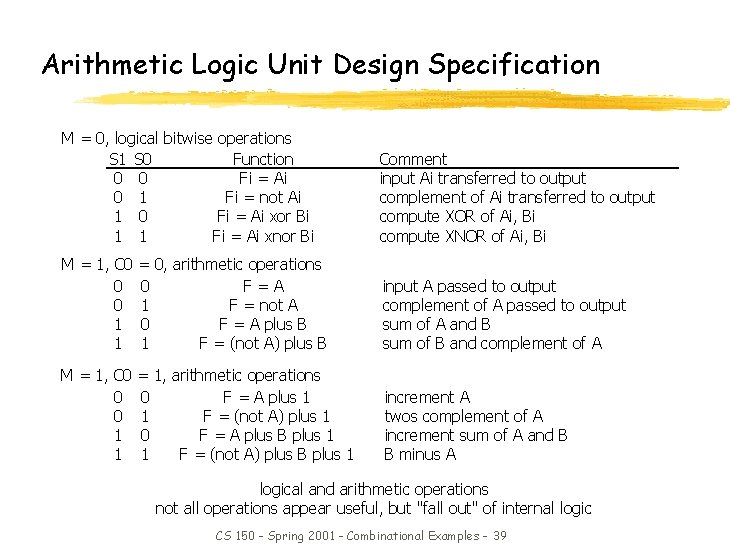
Arithmetic Logic Unit Design Specification M = 0, logical bitwise operations S 1 S 0 Function 0 0 Fi = Ai 0 1 Fi = not Ai 1 0 Fi = Ai xor Bi 1 1 Fi = Ai xnor Bi Comment input Ai transferred to output complement of Ai transferred to output compute XOR of Ai, Bi compute XNOR of Ai, Bi M = 1, C 0 0 0 1 1 = 0, arithmetic operations 0 F=A 1 F = not A 0 F = A plus B 1 F = (not A) plus B input A passed to output complement of A passed to output sum of A and B sum of B and complement of A M = 1, C 0 0 0 1 1 = 1, arithmetic operations 0 F = A plus 1 1 F = (not A) plus 1 0 F = A plus B plus 1 1 F = (not A) plus B plus 1 increment A twos complement of A increment sum of A and B B minus A logical and arithmetic operations not all operations appear useful, but "fall out" of internal logic CS 150 - Spring 2001 - Combinational Examples - 39
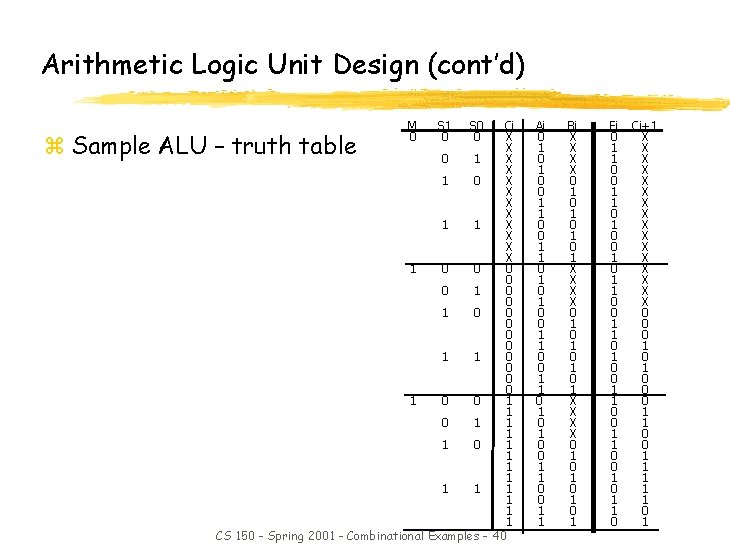
Arithmetic Logic Unit Design (cont’d) S 1 0 S 0 0 Ci X X 0 1 X X 1 0 X X 1 1 X X 0 0 1 0 0 0 1 1 1 0 1 1 1 CS 150 - Spring 2001 - Combinational Examples - 40 z Sample ALU – truth table M 0 Ai 0 1 0 1 0 0 1 1 0 1 0 0 1 1 Bi X X X X 0 1 0 1 X X 0 1 0 1 Fi 0 1 1 0 1 0 0 1 0 1 1 0 Ci+1 X X X X 0 0 0 1 1 1 1 1 0 1
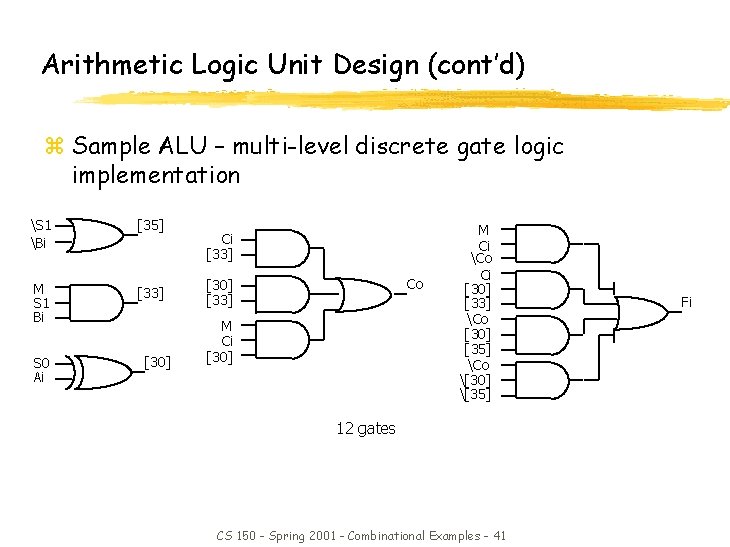
Arithmetic Logic Unit Design (cont’d) z Sample ALU – multi-level discrete gate logic implementation S 1 Bi [35] M S 1 Bi [33] S 0 Ai [30] Ci [33] Co [30] [33] M Ci [30] M Ci Co Ci [30] [33] Co [30] [35] Co [30] [35] 12 gates CS 150 - Spring 2001 - Combinational Examples - 41 Fi
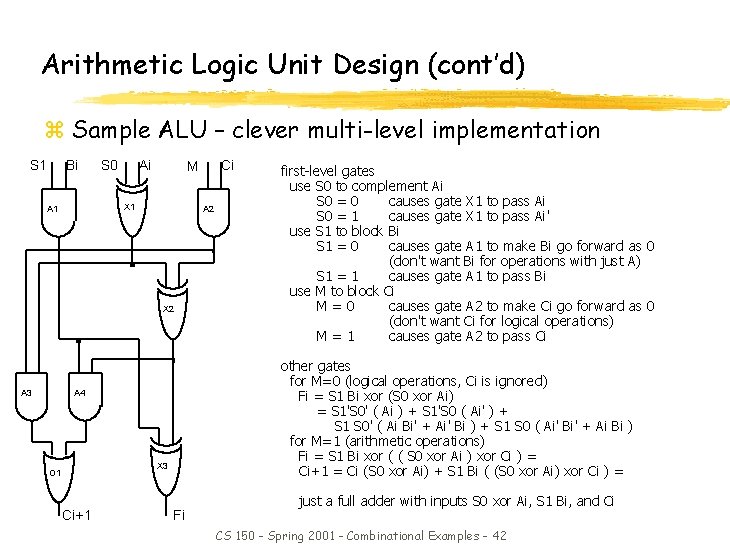
Arithmetic Logic Unit Design (cont’d) z Sample ALU – clever multi-level implementation S 1 Bi S 0 Ai X 1 A 2 X 2 A 3 X 3 Ci+1 first-level gates use S 0 to complement Ai S 0 = 0 causes gate X 1 to pass Ai S 0 = 1 causes gate X 1 to pass Ai' use S 1 to block Bi S 1 = 0 causes gate A 1 to make Bi go forward as 0 (don't want Bi for operations with just A) S 1 = 1 causes gate A 1 to pass Bi use M to block Ci M=0 causes gate A 2 to make Ci go forward as 0 (don't want Ci for logical operations) M=1 causes gate A 2 to pass Ci other gates for M=0 (logical operations, Ci is ignored) Fi = S 1 Bi xor (S 0 xor Ai) = S 1'S 0' ( Ai ) + S 1'S 0 ( Ai' ) + S 1 S 0' ( Ai Bi' + Ai' Bi ) + S 1 S 0 ( Ai' Bi' + Ai Bi ) for M=1 (arithmetic operations) Fi = S 1 Bi xor ( ( S 0 xor Ai ) xor Ci ) = Ci+1 = Ci (S 0 xor Ai) + S 1 Bi ( (S 0 xor Ai) xor Ci ) = A 4 O 1 Ci M Fi just a full adder with inputs S 0 xor Ai, S 1 Bi, and Ci CS 150 - Spring 2001 - Combinational Examples - 42

Summary for Examples of Combinational Logic z Combinational logic design process y Formalize problem: encodings, truth-table, equations y Choose implementation tech (ROM, PAL, PLA, discrete gates) y Implement by following the design procedure for that technology z Binary number representation y Positive numbers the same y Difference is in how negative numbers are represented y 2 s complement easiest to handle: one representation for zero, slightly complicated complementation, simple addition z Circuits for binary addition y Basic half-adder and full-adder y Carry lookahead logic y Carry-select z ALU Design y Specification, implementation CS 150 - Spring 2001 - Combinational Examples - 43
- Slides: 43