Combinational Logic Circuits Chapter 2 Mano and Kime

Combinational Logic Circuits Chapter 2 Mano and Kime

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

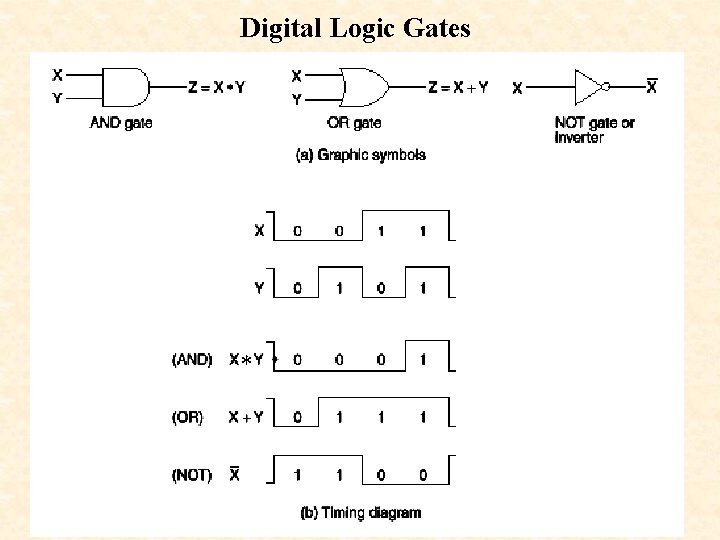
Digital Logic Gates *

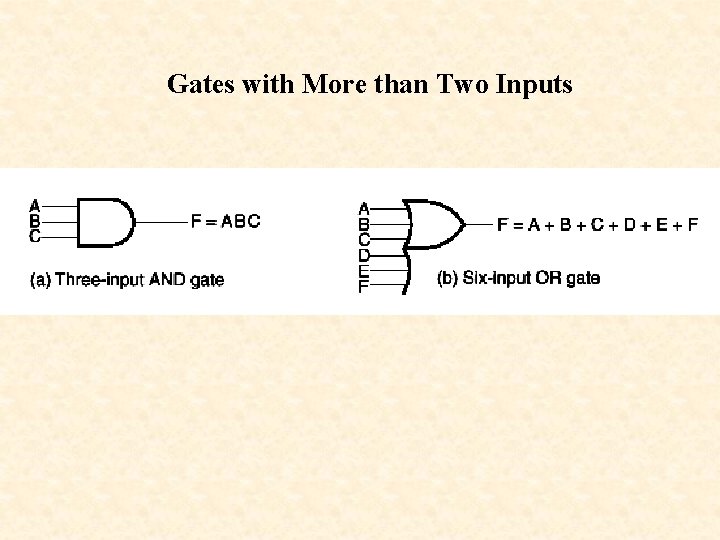
Gates with More than Two Inputs

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

Basic Identities of Boolean Algebra

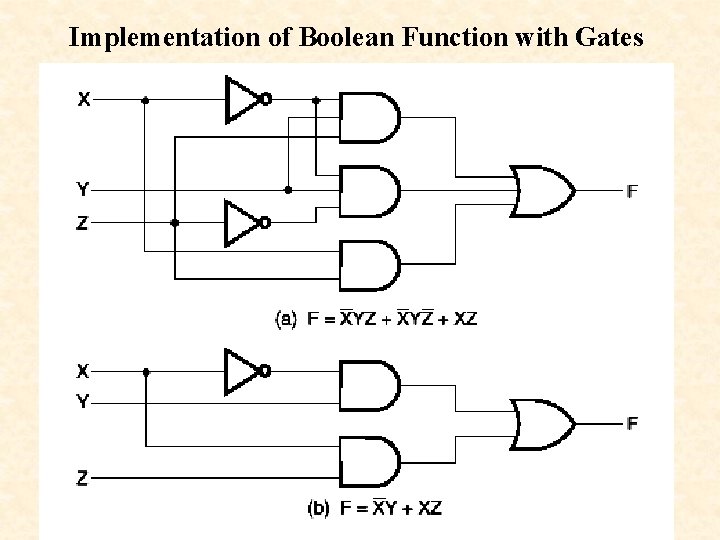
Implementation of Boolean Function with Gates

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

Minterms for Three Variables

Sum of Products Design X 0 0 1 1 Y 0 1 minterms m 0 = !X & !Y m 1 = !X & Y m 2 = X & !Y m 3 = X & Y

Sum of Products Design X 0 0 1 1 Design an XOR gate Y Z 0 0 1 1 m 1 = !X & Y 0 1 m 2 = X & !Y 1 0 Z = m 1 # m 2 = (!X & Y) # (X & !Y)

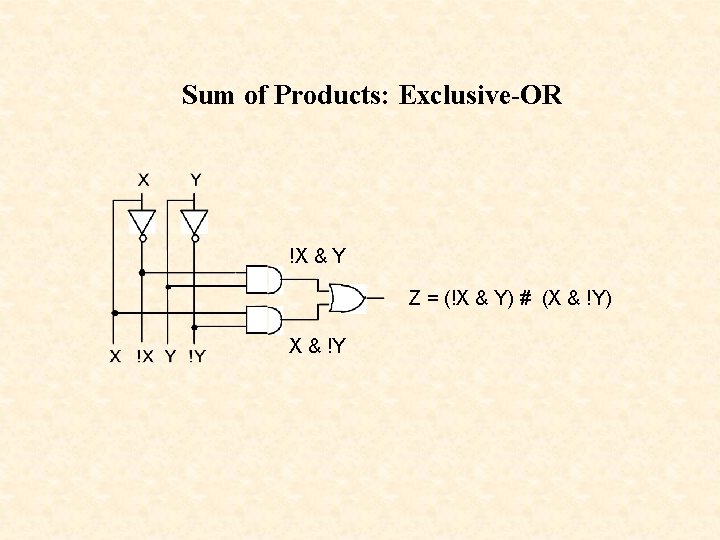
Sum of Products: Exclusive-OR !X & Y Z = (!X & Y) # (X & !Y) X & !Y

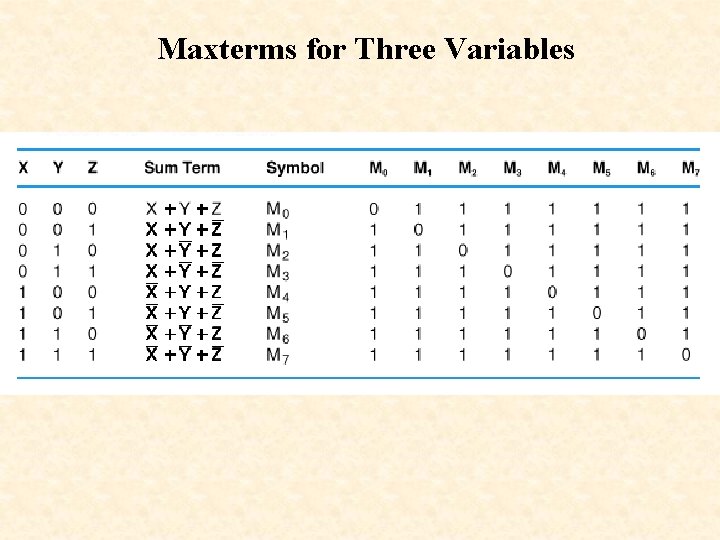
Maxterms for Three Variables

Product of Sums Design Maxterms: A maxterm is NOT a minterm maxterm M 0 = NOT minterm m 0 M 0 = !m 0 = !(!X & !Y) = !!(!!X # !!Y) = X # Y

Product of Sums Design X 0 0 1 1 Y 0 1 minterms m 0 = !X & !Y m 1 = !X & Y m 2 = X & !Y m 3 = X & Y M 0 M 1 M 2 M 3 maxterms = !m 0 = X # Y = !m 1 = X # !Y = !m 2 = !X # Y = !m 3 = !X # !Y

Product of Sums Design an XOR gate X 0 0 1 1 Y 0 1 Z 0 1 1 0 Z is NOT minterm m 0 AND it is NOT minterm m 3

Product of Sums Design X 0 0 1 1 Design an XOR gate Y Z M 0 = X # Y 0 0 1 1 0 1 M 3 = !X # !Y 1 0 Z = M 0 & M 3 = (X # Y) & (!X # !Y)

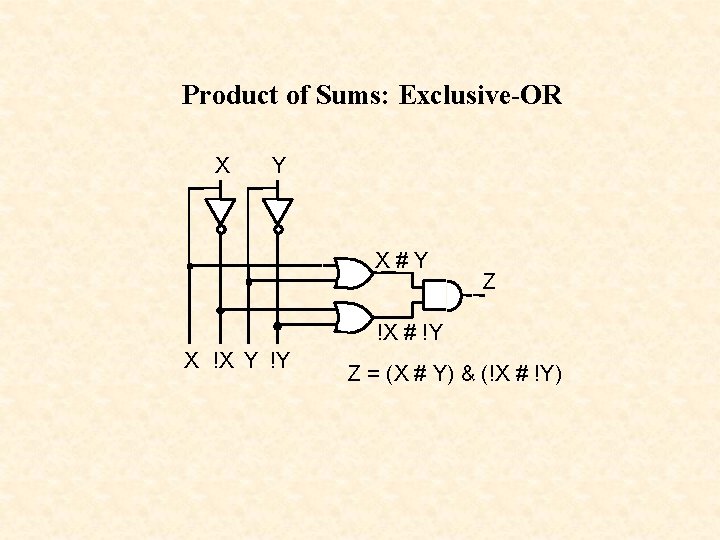
Product of Sums: Exclusive-OR X Y X#Y Z !X # !Y X !X Y !Y Z = (X # Y) & (!X # !Y)

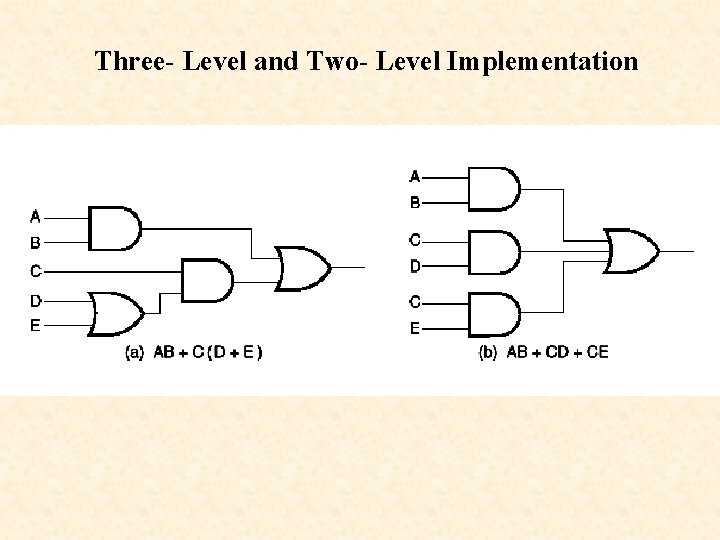
Three- Level and Two- Level Implementation

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

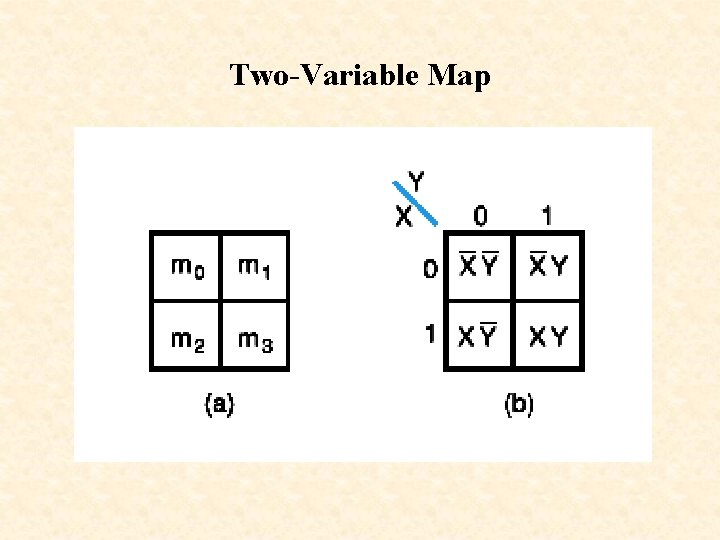
Two-Variable Map

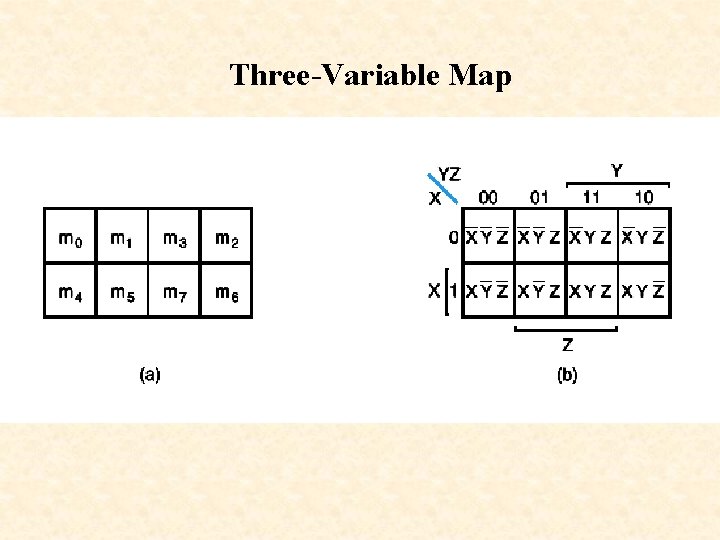
Three-Variable Map

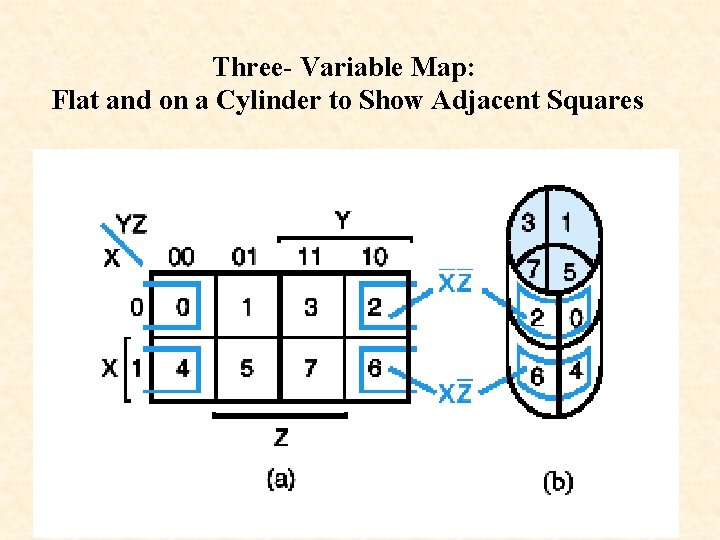
Three- Variable Map: Flat and on a Cylinder to Show Adjacent Squares

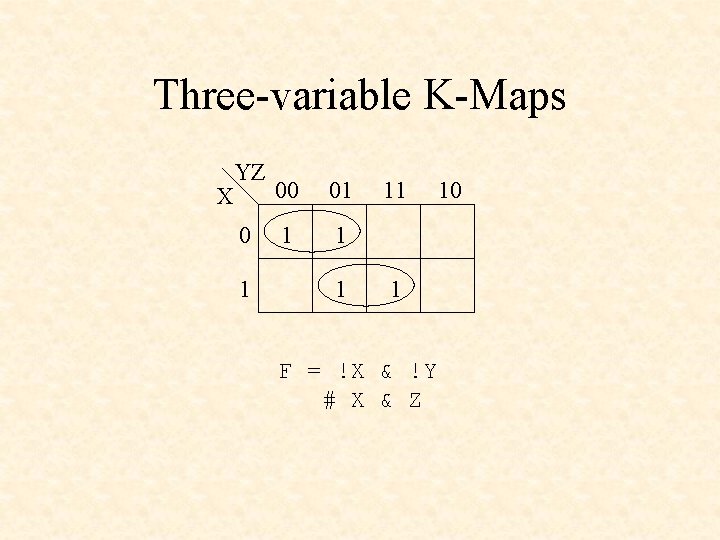
Three-variable K-Maps X YZ 0 1 00 01 1 11 1 F = !X & !Y # X & Z 10

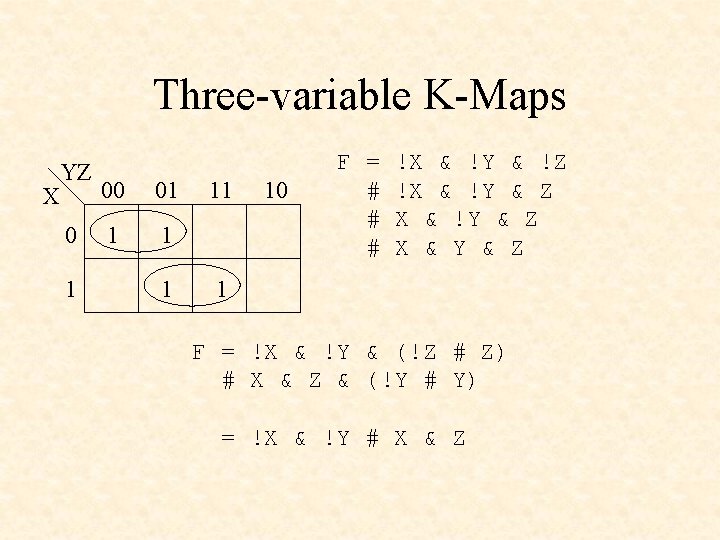
Three-variable K-Maps X YZ 0 1 00 01 1 11 10 F = # # # !X & !Y & !Z !X & !Y & Z X & Y & Z 1 F = !X & !Y & (!Z # Z) # X & Z & (!Y # Y) = !X & !Y # X & Z

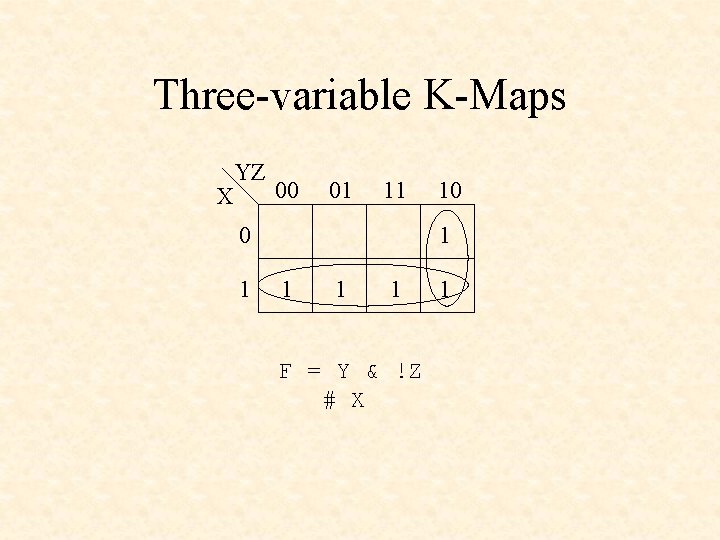
Three-variable K-Maps X YZ 00 01 11 0 1 1 1 1 F = Y & !Z # X 1

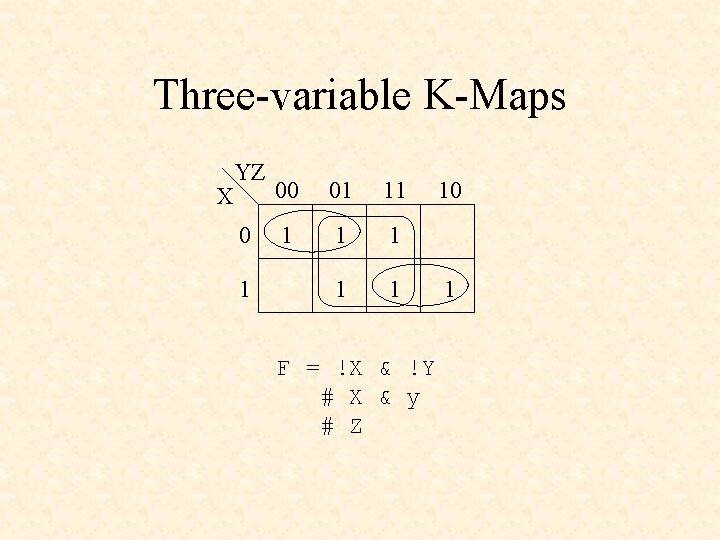
Three-variable K-Maps X YZ 0 1 00 01 11 1 1 F = !X & !Y # X & y # Z 10 1

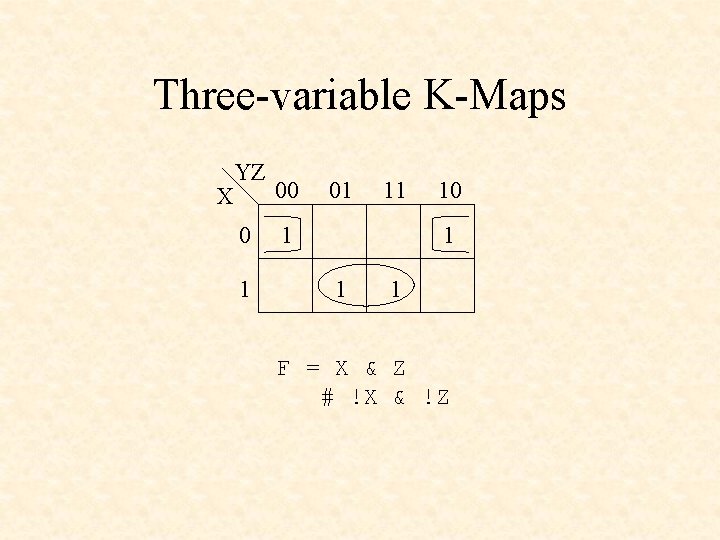
Three-variable K-Maps X YZ 0 1 00 01 11 1 10 1 1 1 F = X & Z # !X & !Z

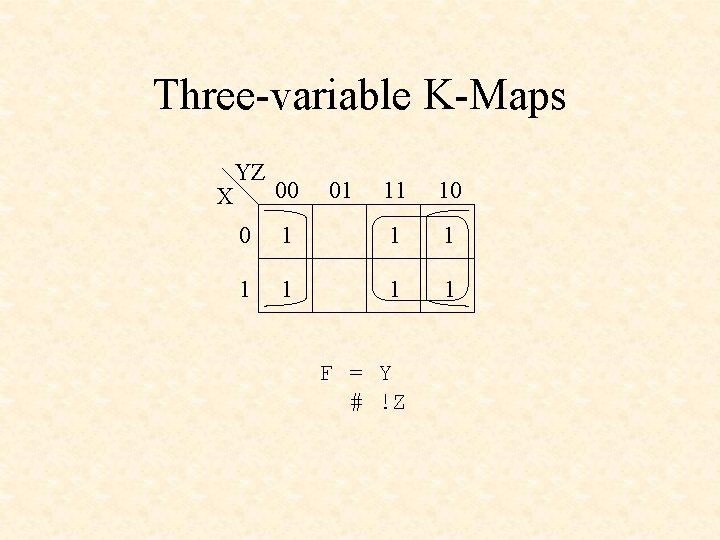
Three-variable K-Maps X YZ 00 01 11 10 0 1 1 1 1 F = Y # !Z

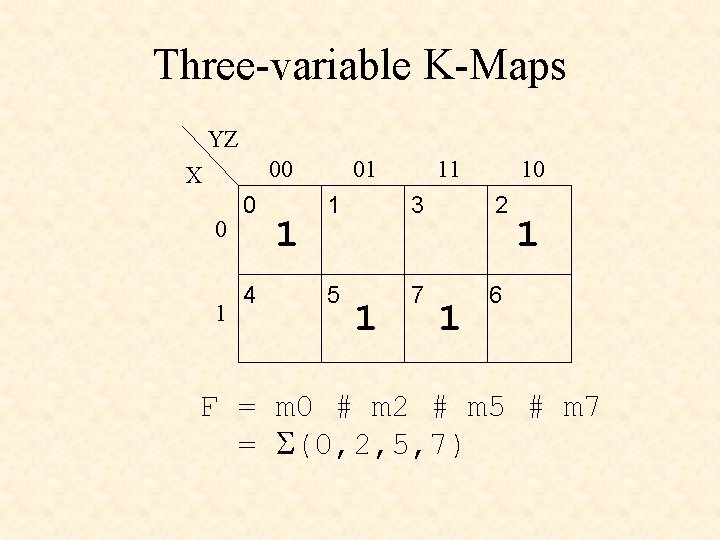
Three-variable K-Maps YZ 00 X 0 1 0 4 1 01 11 10 1 3 2 5 7 6 1 1 1 F = m 0 # m 2 # m 5 # m 7 = S(0, 2, 5, 7)

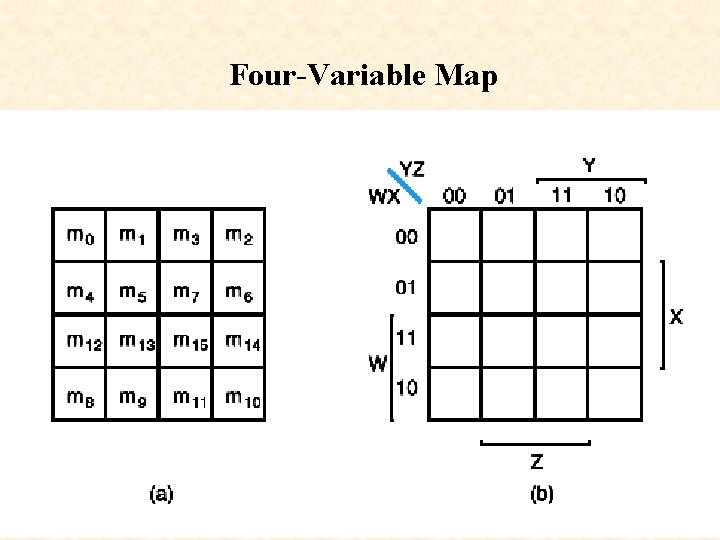
Four-Variable Map

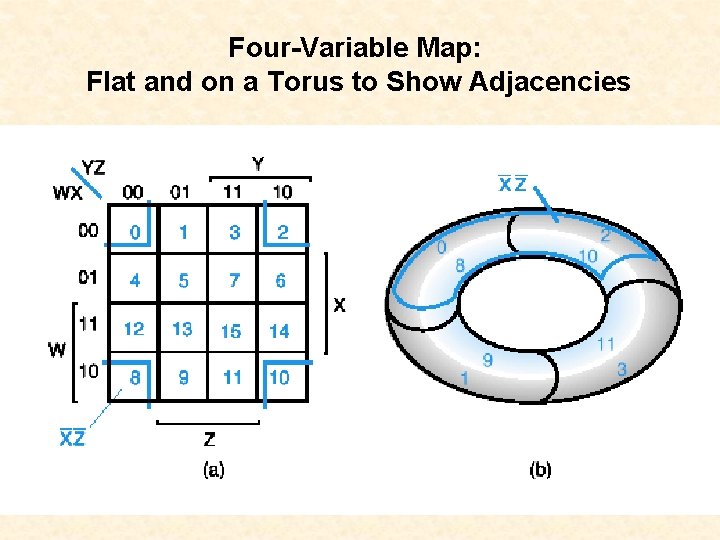
Four-Variable Map: Flat and on a Torus to Show Adjacencies

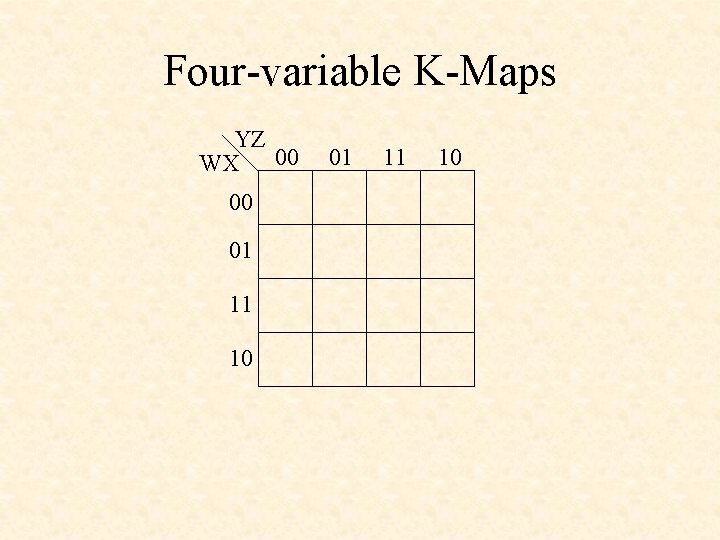
Four-variable K-Maps YZ WX 00 00 01 11 10

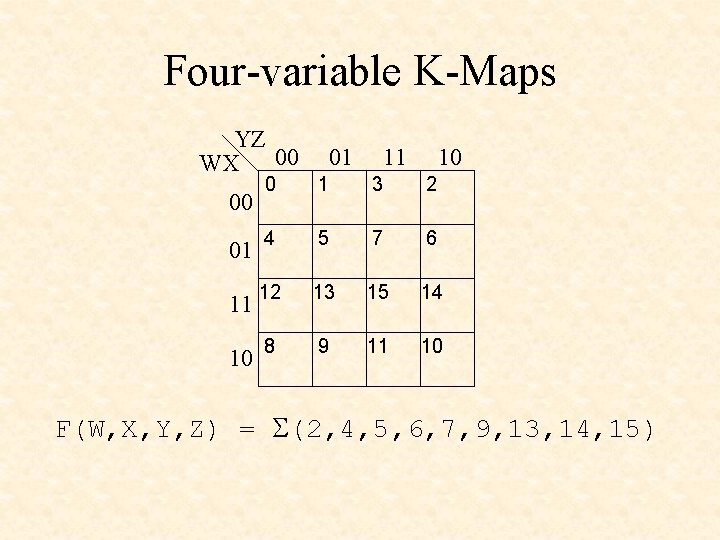
Four-variable K-Maps YZ WX 00 01 11 10 0 1 3 2 01 4 5 7 6 11 12 13 15 14 10 8 9 11 10 00 F(W, X, Y, Z) = S(2, 4, 5, 6, 7, 9, 13, 14, 15)

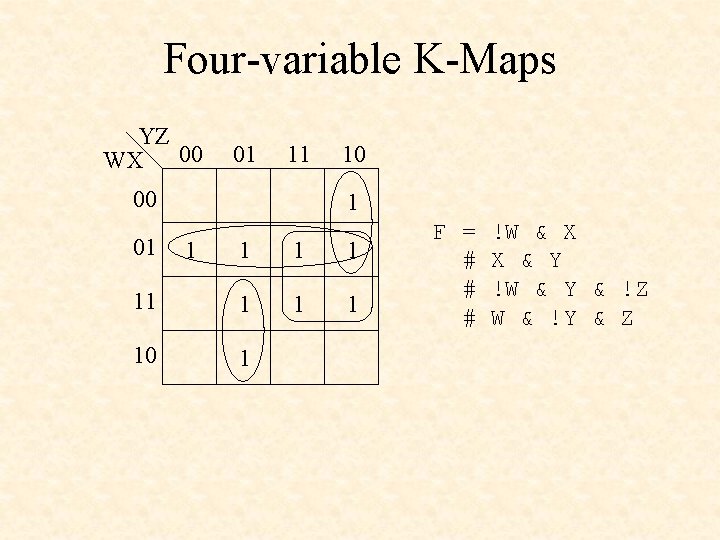
Four-variable K-Maps YZ WX 00 01 11 00 01 10 1 1 11 1 10 1 F = # # # !W & X X & Y !W & Y & !Z W & !Y & Z

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

Prime Implicants F = X & !Y & Z # !X & !Z # !X & Y Each product term is an implicant A product term that cannot have any of its variables removed and still imply the logic function is called a prime implicant.

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

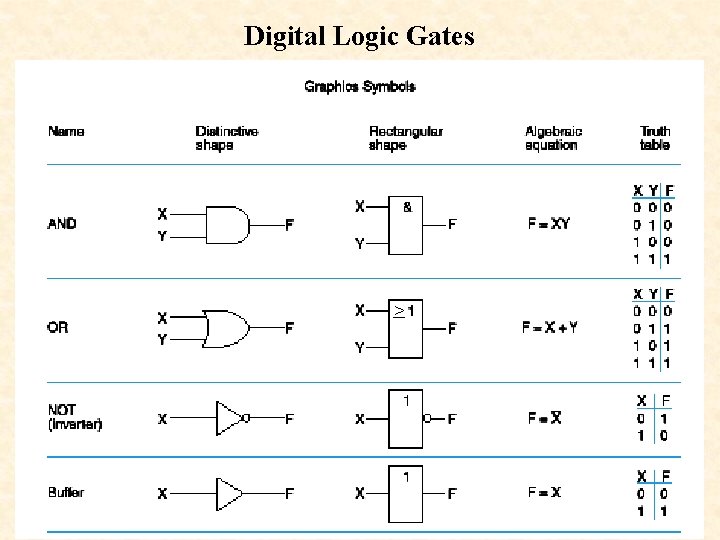
Digital Logic Gates >

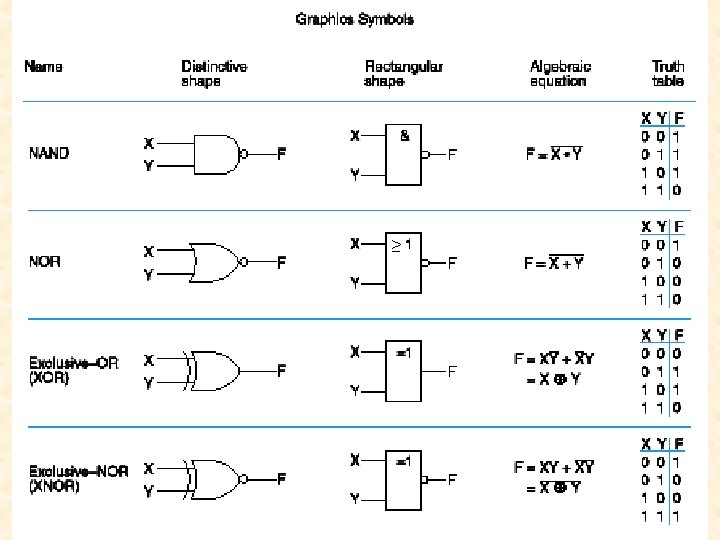
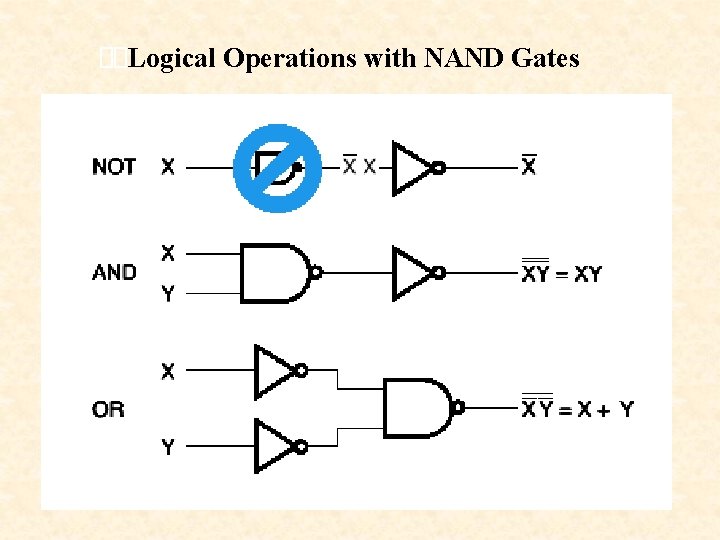
Logical Operations with NAND Gates

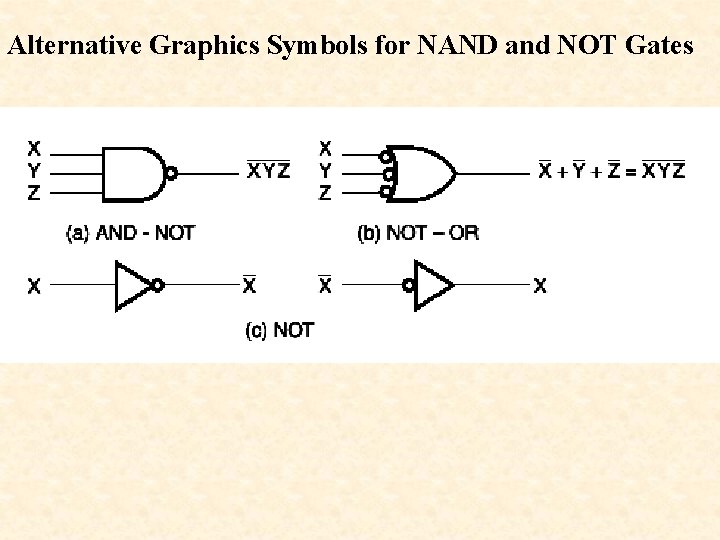
Alternative Graphics Symbols for NAND and NOT Gates

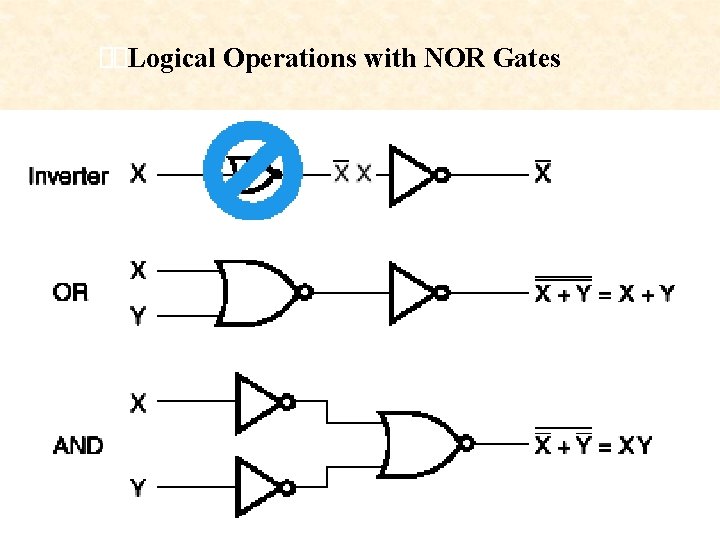
Logical Operations with NOR Gates

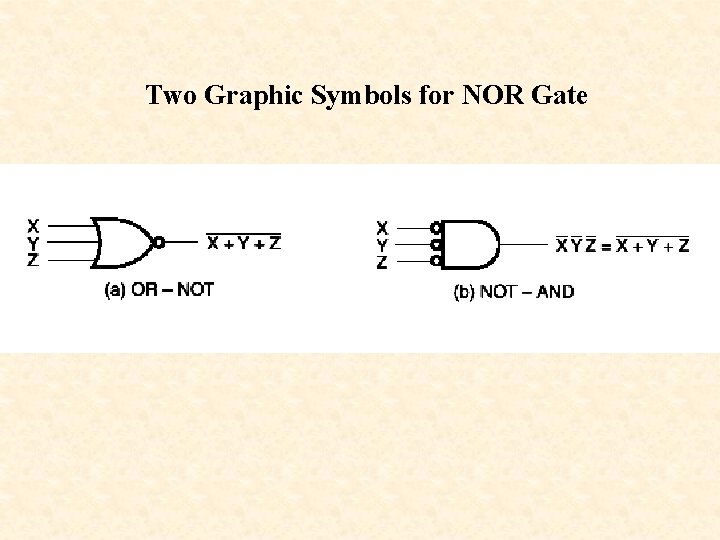
Two Graphic Symbols for NOR Gate

Demonstration of Positive and Negative Logic

Generalized De Morgan’s Theorem • • NOT all variables Change & to # and # to & NOT the result ----------------------F=X&Y#X&Z#Y&Z F = !((!X # !Y) & (!X # !Z) & (!Y # !Z)) F = !(!(X & Y) & !(X & Z) & !(Y & Z))

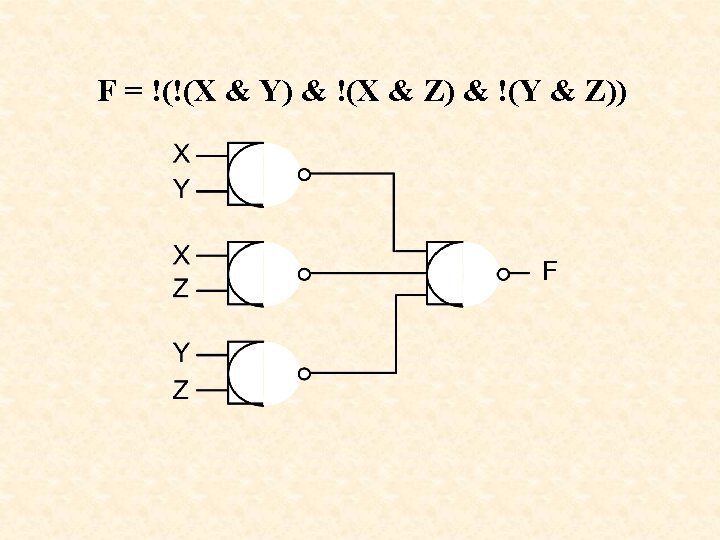
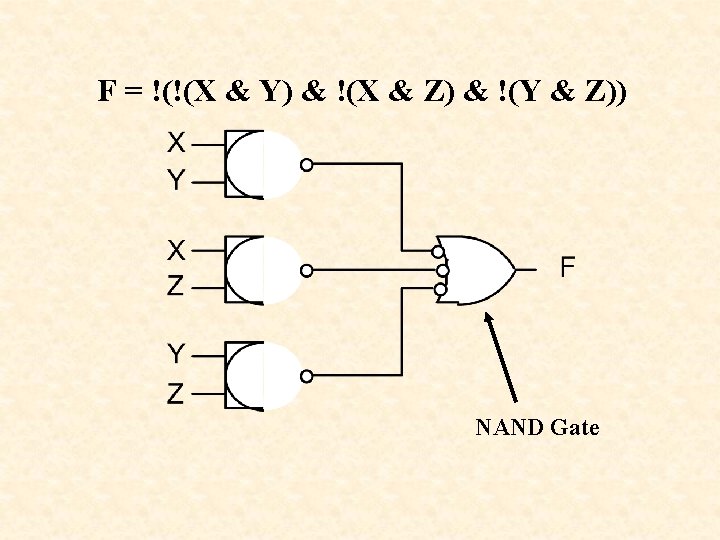
F = !(!(X & Y) & !(X & Z) & !(Y & Z)) NAND Gate

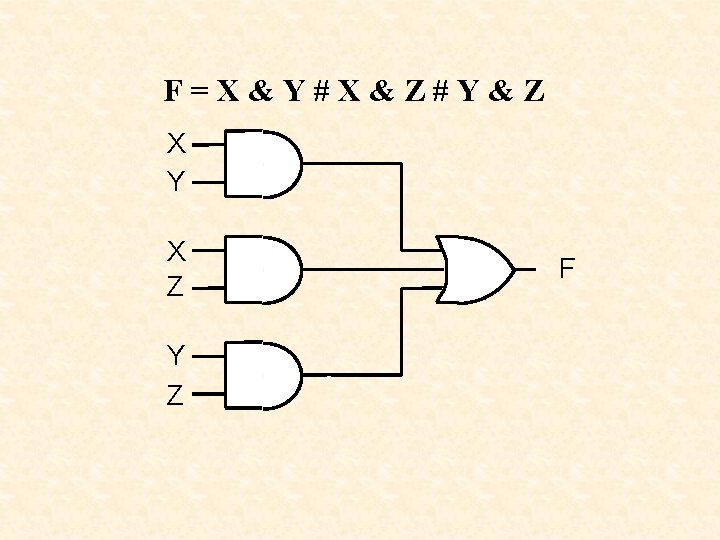
F=X&Y#X&Z#Y&Z X Y X Z Y Z F

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

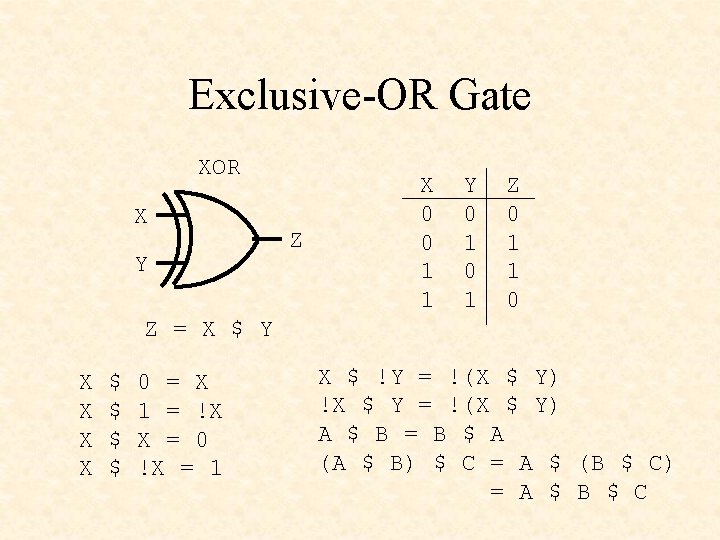
Exclusive-OR Gate XOR X Y Z X 0 0 1 1 Y 0 1 Z 0 1 1 0 Z = X $ Y X X $ $ 0 = X 1 = !X X = 0 !X = 1 X $ !Y = !(X $ Y) !X $ Y = !(X $ Y) A $ B = B $ A (A $ B) $ C = A $ (B $ C) = A $ B $ C

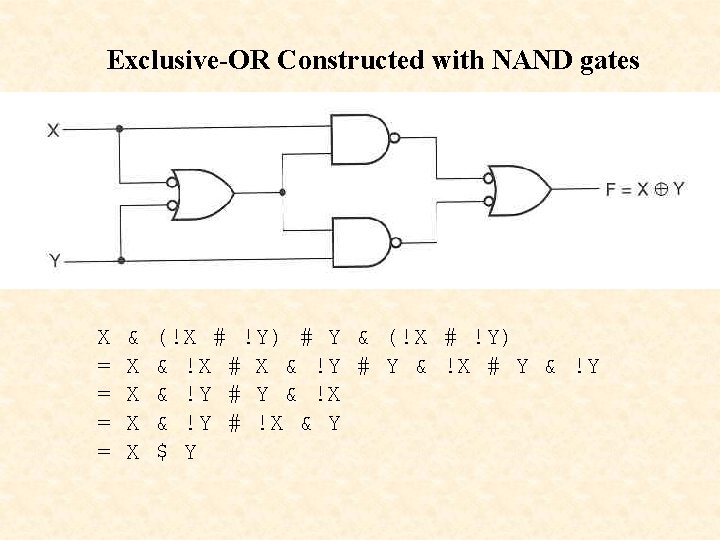
Exclusive-OR Constructed with NAND gates X = = & X X (!X # !Y) # Y & (!X # !Y) & !X # X & !Y # Y & !X # Y & !Y # Y & !X & !Y # !X & Y $ Y

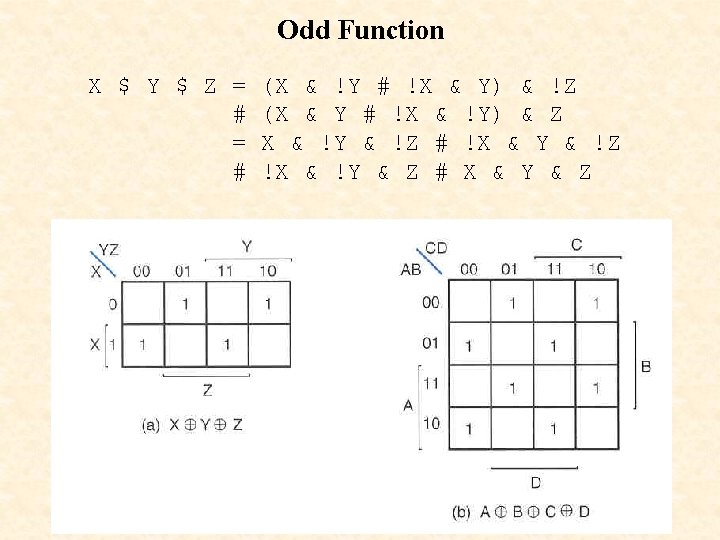
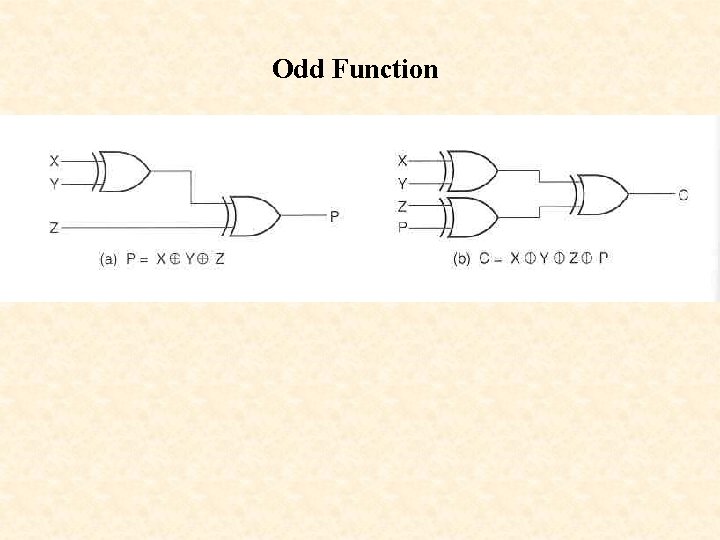
Odd Function

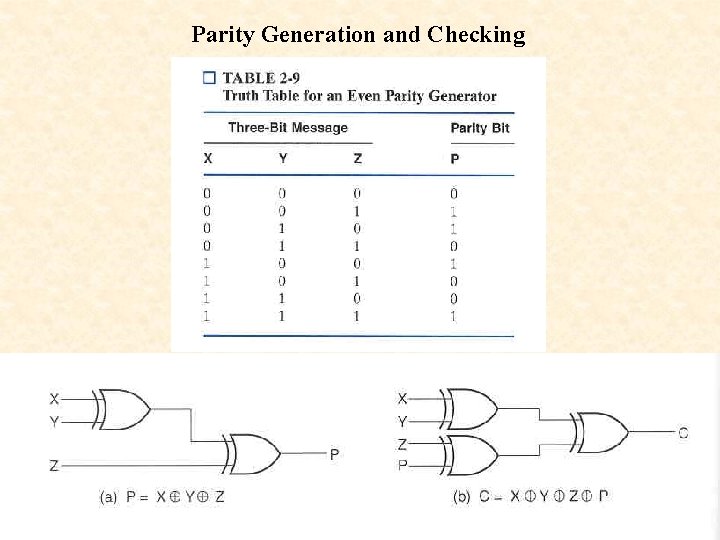
Parity Generation and Checking

Combinational Logic Circuits • • Binary Logic and Gates Boolean Algebra Standard Forms Map Simplification Map Manipulation NAND and NOR Gates Exclusive-OR Gates Integrated Circuits

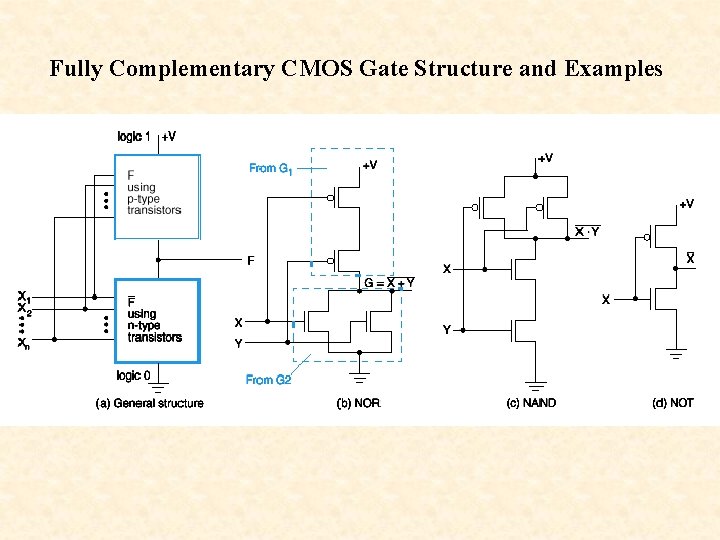
Fully Complementary CMOS Gate Structure and Examples

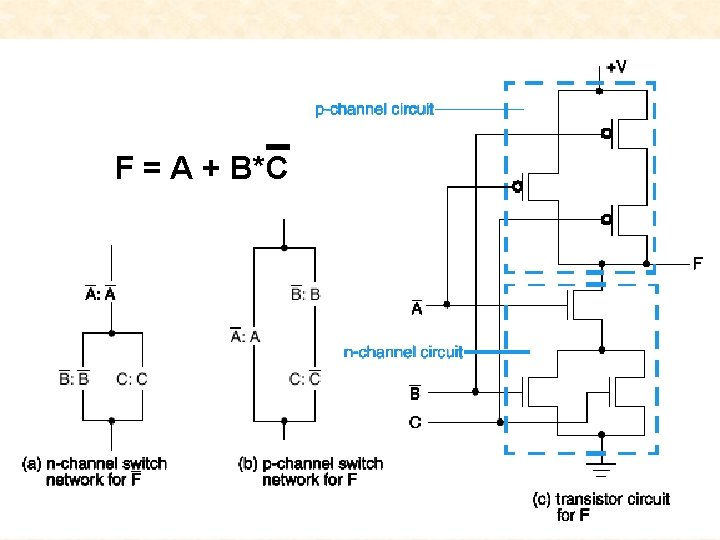
F = A + B*C

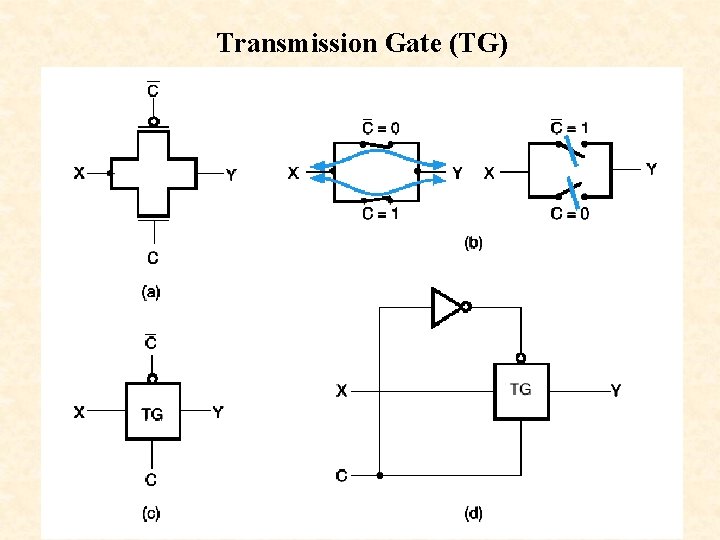
Transmission Gate (TG)

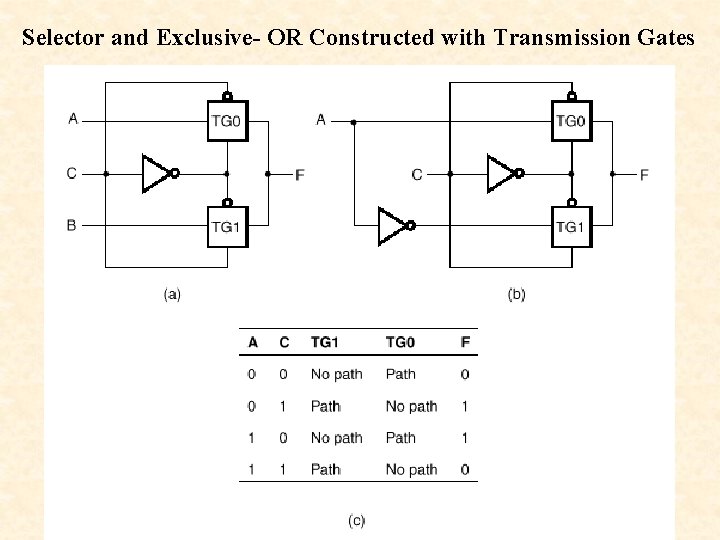
Selector and Exclusive- OR Constructed with Transmission Gates