Combinational Circuit Design EE 200 Digital Logic Circuit

Combinational Circuit Design EE 200 Digital Logic Circuit Design Dr. Muhamed Mudawar King Fahd University of Petroleum and Minerals

Presentation Outline v How to Design a Combinational Circuit v Designing a BCD to Excess-3 Code Converter v Designing a BCD to 7 -Segment Decoder v Hierarchical Design v Iterative Design Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 2

Combinational Circuit v Combinational Circuit Design Circuit EE 200 – Digital Logic Circuit Design Combinational © Muhamed Mudawar – slide 3

How to Design a Combinational Circuit 1. Specification ² Specify the inputs, outputs, and what the circuit should do 2. Formulation ² Convert the specification into truth tables or logic expressions for outputs 3. Logic Minimization ² Minimize the output functions using K-map or Boolean algebra 4. Technology Mapping ² Draw a logic diagram using ANDs, ORs, and inverters ² Map the logic diagram into the selected technology ² Considerations: cost, delays, fan-in, fan-out 5. Verification ² Verify the correctness of the design, either manually or using simulation Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 4

Designing a BCD to Excess-3 Code Converter v Combinational Circuit Design EE 200 – Digital Logic Circuit Design BCD Excess-3 a b c d w x y z 0 0 0 1 1 0 0 0 1 0 0 1 1 0 0 0 1 1 1 0 0 1 1 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 0 1010 to 1111 X X © Muhamed Mudawar – slide 5

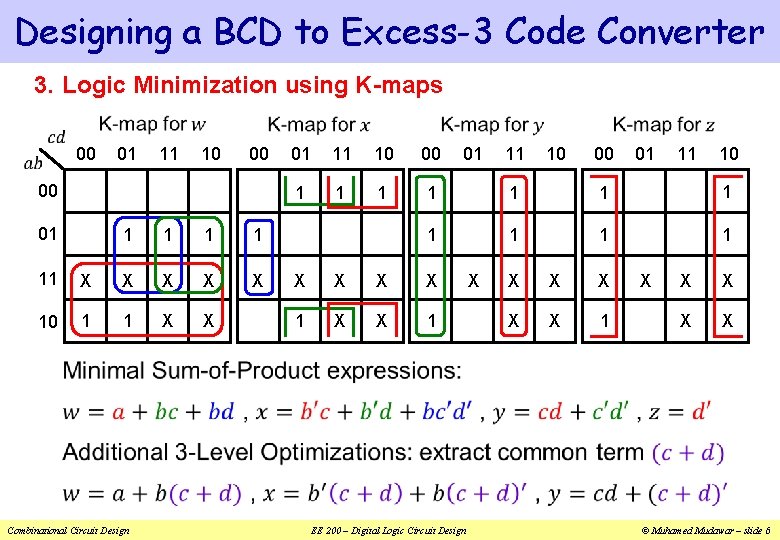
Designing a BCD to Excess-3 Code Converter 3. Logic Minimization using K-maps 00 01 11 10 00 00 01 1 1 X 11 X X 10 1 1 X X Combinational Circuit Design 01 11 10 00 1 1 1 X X 1 01 EE 200 – Digital Logic Circuit Design X 11 10 00 X X X 1 01 X 11 10 X X © Muhamed Mudawar – slide 6

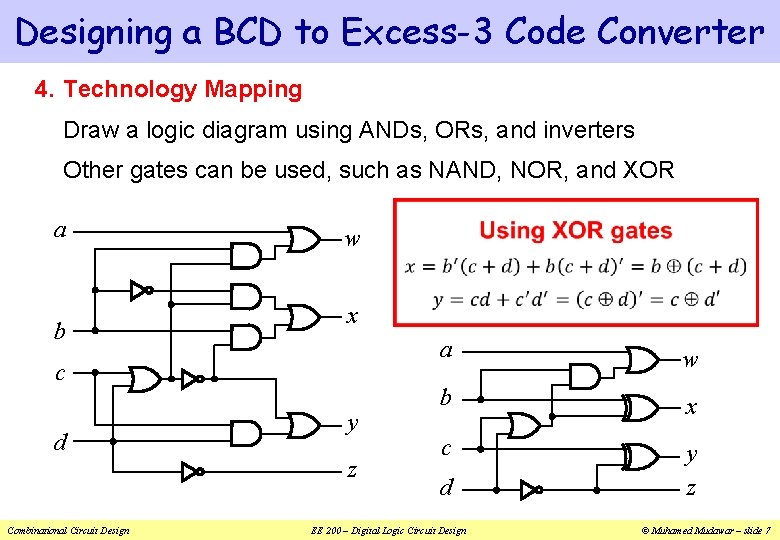
Designing a BCD to Excess-3 Code Converter 4. Technology Mapping Draw a logic diagram using ANDs, ORs, and inverters Other gates can be used, such as NAND, NOR, and XOR a b w x c d y z Combinational Circuit Design a w b x c y z d EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 7

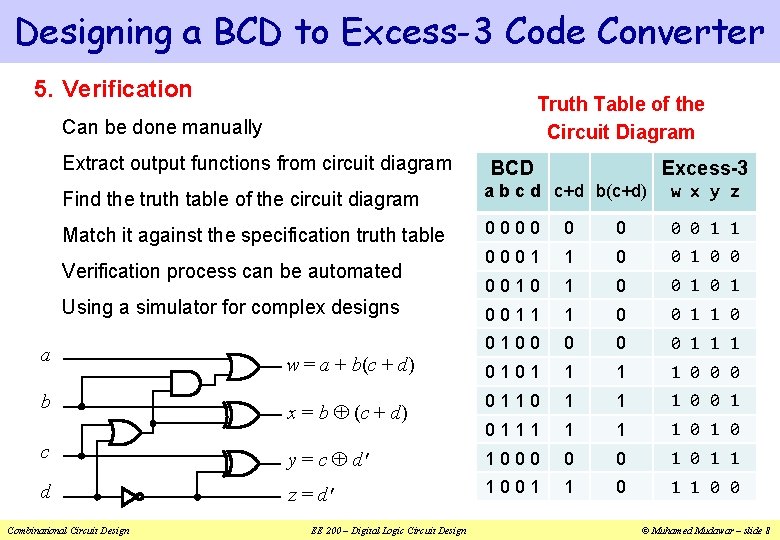
Designing a BCD to Excess-3 Code Converter 5. Verification Truth Table of the Circuit Diagram Can be done manually Extract output functions from circuit diagram BCD Excess-3 Find the truth table of the circuit diagram a b c d c+d b(c+d) w x y z Match it against the specification truth table 0000 0 0 1 1 0001 1 0 0 0010 1 0 1 0011 1 0 0100 0 0 w = a + b(c + d) 0 1 1 1 0101 1 0 0 0 x = b (c + d) 0110 1 1 1 0 0 1 0111 1 0 1 0 c y = c d' 1000 0 0 1 1 d z = d' 1001 1 0 0 Verification process can be automated Using a simulator for complex designs a b Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 8

BCD to 7 -Segment Decoder v Seven-Segment Display: ² Made of Seven segments: light-emitting diodes (LED) ² Found in electronic devices: such as clocks, calculators, etc. v BCD to 7 -Segment Decoder A B C D BCD to 7 -Segment Decoder ² Accepts as input a BCD decimal digit (0 to 9) a b c d e f g ² Generates output to the seven LED segments to display the BCD digit ² Each segment can be turned on or off separately Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 9

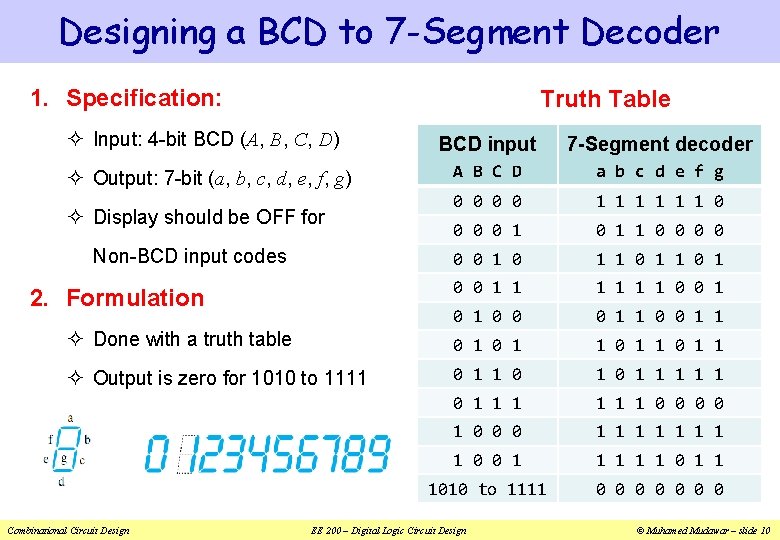
Designing a BCD to 7 -Segment Decoder 1. Specification: Truth Table ² Input: 4 -bit BCD (A, B, C, D) BCD input 7 -Segment decoder A B C D a b c d e f g 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 1 0 0 0 1 1 ² Done with a truth table 0 1 1 ² Output is zero for 1010 to 1111 0 1 0 1 1 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 1010 to 1111 0 0 0 0 ² Output: 7 -bit (a, b, c, d, e, f, g) ² Display should be OFF for Non-BCD input codes 2. Formulation Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 10

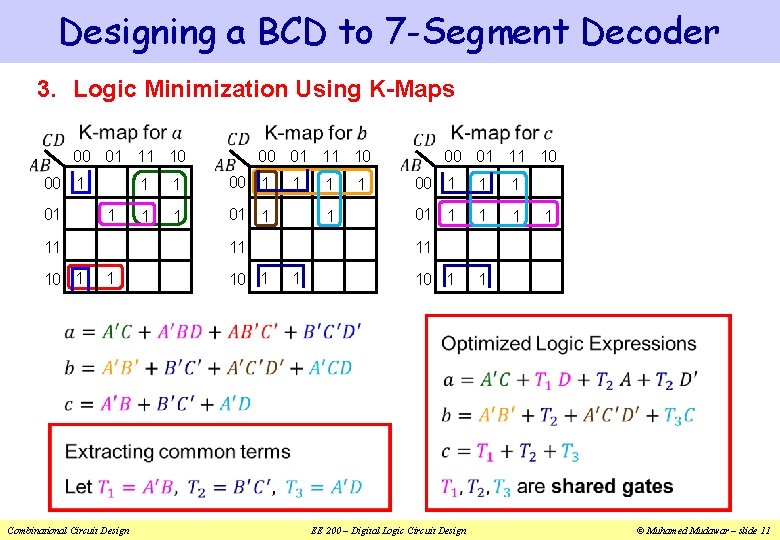
Designing a BCD to 7 -Segment Decoder 3. Logic Minimization Using K-Maps 00 01 11 10 00 1 01 1 1 00 1 1 1 01 1 Combinational Circuit Design 10 1 11 11 10 1 1 1 00 01 11 10 00 1 1 1 01 1 1 11 1 10 1 EE 200 – Digital Logic Circuit Design 1 © Muhamed Mudawar – slide 11

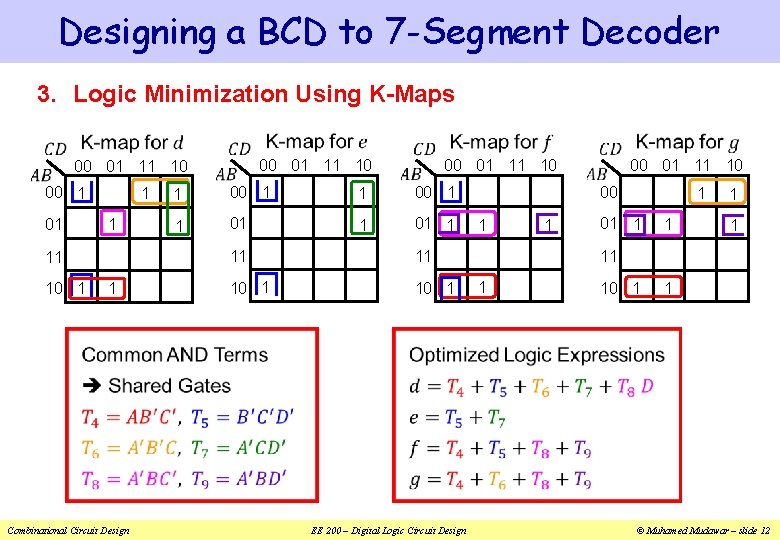
Designing a BCD to 7 -Segment Decoder 3. Logic Minimization Using K-Maps 00 1 01 1 1 11 10 1 1 Combinational Circuit Design 00 01 11 10 1 00 1 1 01 1 11 11 10 1 EE 200 – Digital Logic Circuit Design 00 01 11 10 00 1 1 1 01 1 1 11 1 10 1 1 © Muhamed Mudawar – slide 12

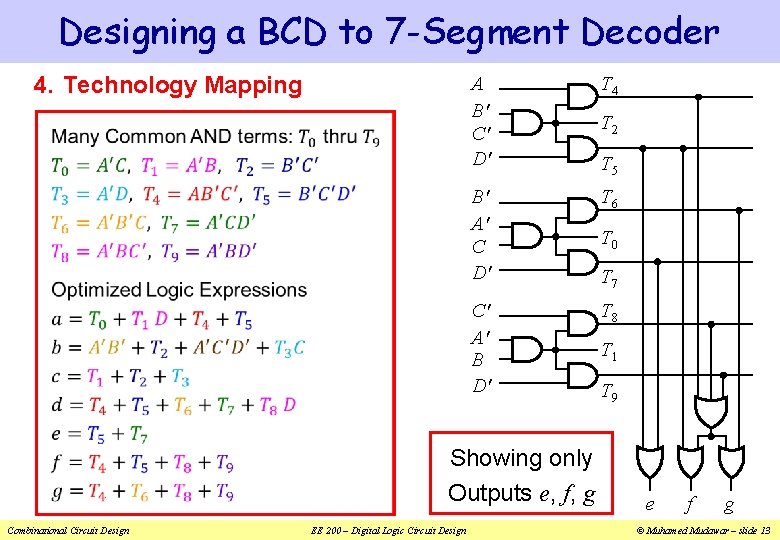
Designing a BCD to 7 -Segment Decoder 4. Technology Mapping A B' C' D' T 4 B' A' C D' T 6 C' A' B D' T 8 Showing only Outputs e, f, g Combinational Circuit Design EE 200 – Digital Logic Circuit Design T 2 T 5 T 0 T 7 T 1 T 9 e f g © Muhamed Mudawar – slide 13

Verification Methods v Manual Logic Analysis ² Find the logic expressions and truth table of the final circuit ² Compare the final circuit truth table against the specified truth table ² Compare the circuit output expressions against the specified expressions ² Tedious for large designs + Human Errors v Simulation ² Simulate the final circuit, possibly written in HDL (such as Verilog) ² Write a test bench that automates the verification process ² Generate test cases for ALL possible inputs (exhaustive testing) ² Verify the output correctness for ALL input test cases ² Exhaustive testing can be very time consuming for many inputs Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 14

Hierarchical Design v Why Hierarchical Design? To simplify the implementation of a complex circuit v What is Hierarchical Design? Decompose a complex circuit into smaller pieces called blocks Decompose each block into even smaller blocks Repeat as necessary until the blocks are small enough Any block not decomposed is called a primitive block The hierarchy is a tree of blocks at different levels v The blocks are verified and well-document v They are placed in a library for future use Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 15

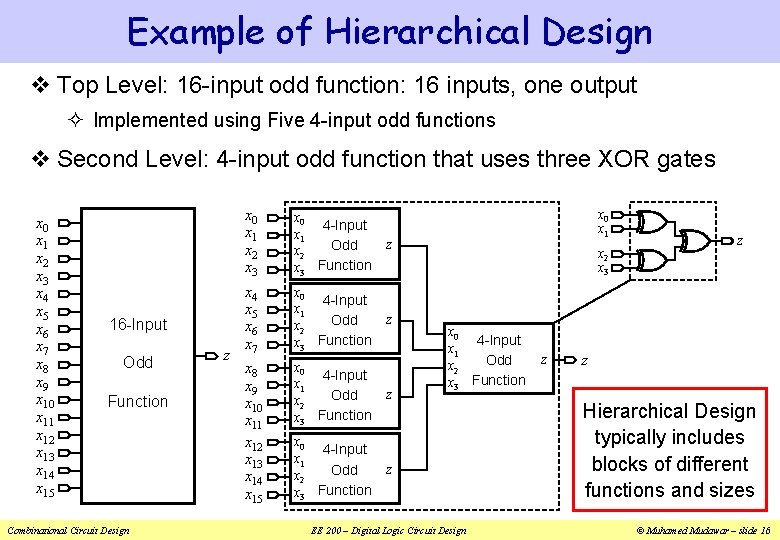
Example of Hierarchical Design v Top Level: 16 -input odd function: 16 inputs, one output ² Implemented using Five 4 -input odd functions v Second Level: 4 -input odd function that uses three XOR gates x 0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 16 -Input Odd Function Combinational Circuit Design z x 0 x 1 x 2 x 3 x 0 4 -Input x 1 Odd x 2 x 3 Function z x 4 x 5 x 6 x 7 x 0 4 -Input x 1 Odd x 2 x 3 Function z x 8 x 9 x 10 x 11 x 12 x 13 x 14 x 15 x 0 4 -Input x 1 Odd x 2 x 3 Function z x 0 x 1 x 2 x 3 x 0 4 -Input x 1 Odd x 2 x 3 Function EE 200 – Digital Logic Circuit Design z z z Hierarchical Design typically includes blocks of different functions and sizes © Muhamed Mudawar – slide 16

Top-Down versus Bottom-Up Design v A top-down design proceeds from a high-level specification to a more and more detailed design by decomposition and successive refinement v A bottom-up design starts with detailed primitive blocks and combines them into larger and more complex functional blocks v Design usually proceeds top-down to a known set of building blocks, ranging from complete processors to primitive logic gates Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 17

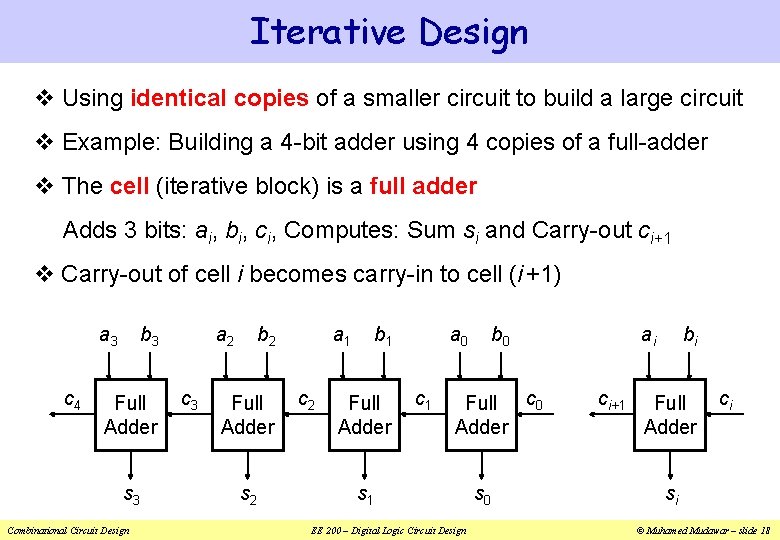
Iterative Design v Using identical copies of a smaller circuit to build a large circuit v Example: Building a 4 -bit adder using 4 copies of a full-adder v The cell (iterative block) is a full adder Adds 3 bits: ai, bi, ci, Computes: Sum si and Carry-out ci+1 v Carry-out of cell i becomes carry-in to cell (i +1) a 3 c 4 b 3 Full Adder s 3 Combinational Circuit Design a 2 c 3 b 2 Full Adder s 2 a 1 c 2 b 1 Full Adder a 0 c 1 b 0 Full c 0 Adder s 1 EE 200 – Digital Logic Circuit Design s 0 ai ci+1 bi Full Adder ci si © Muhamed Mudawar – slide 18

Full Adder v Full adder adds 3 bits: a, b, and c v Two output bits: Truth Table a b c cout sum 1. Carry bit: cout 0 0 0 2. Sum bit: sum 0 0 1 0 1 0 0 1 the input is odd (odd function) 0 1 1 1 0 sum = (a b) c 1 0 0 0 1 1 0 1 1 1 v Sum bit is 1 if the number of 1's in v Carry bit is 1 if the number of 1's in the input is 2 or 3 cout = a·b + (a b)·c Combinational Circuit Design EE 200 – Digital Logic Circuit Design © Muhamed Mudawar – slide 19