Combinational Building Blocks 21 Multiplexor MUX I 0

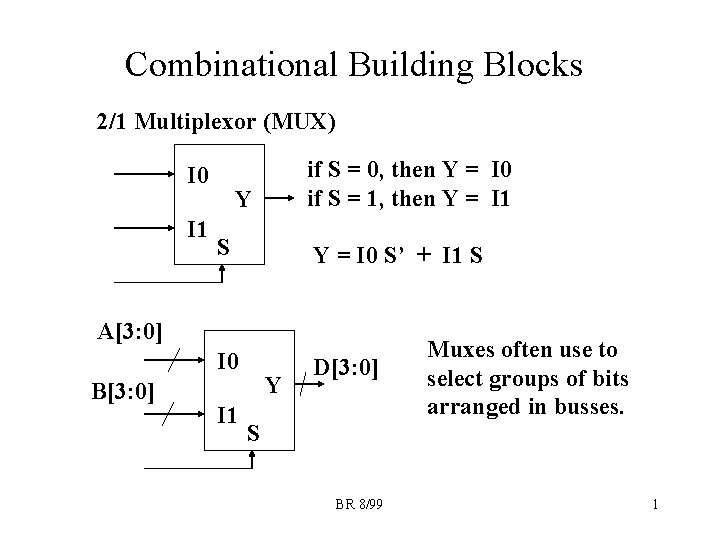
Combinational Building Blocks 2/1 Multiplexor (MUX) I 0 I 1 if S = 0, then Y = I 0 if S = 1, then Y = I 1 Y S Y = I 0 S’ + I 1 S A[3: 0] I 0 B[3: 0] I 1 Y D[3: 0] S BR 8/99 Muxes often use to select groups of bits arranged in busses. 1

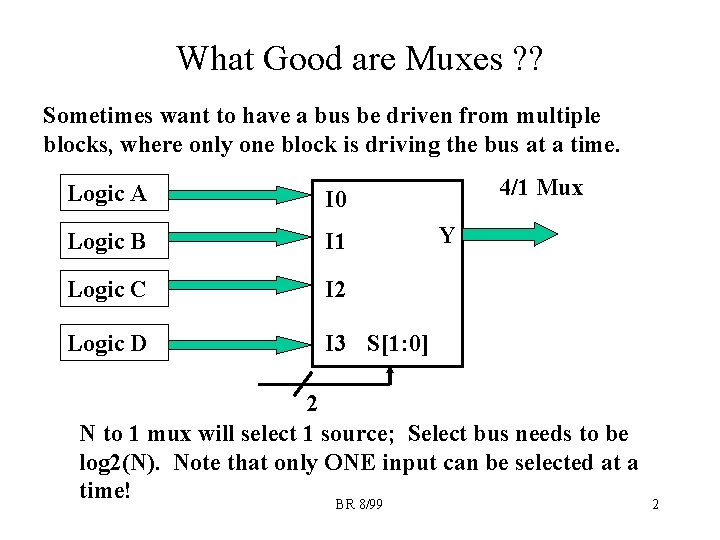
What Good are Muxes ? ? Sometimes want to have a bus be driven from multiple blocks, where only one block is driving the bus at a time. Logic A I 0 Logic B I 1 Logic C I 2 Logic D I 3 S[1: 0] 4/1 Mux Y 2 N to 1 mux will select 1 source; Select bus needs to be log 2(N). Note that only ONE input can be selected at a time! BR 8/99 2

Higher Order Muxes 4/1 Mux I 0 I 1 Y I 2 I 3 S[1: 0] 8/1 Mux I 0 I 1 Y I 2 I 3 I 4 I 5 I 6 I 7 S[2: 0] 2 if S = “ 00”, then Y = if S = “ 01”, then Y = if S = “ 10”, then Y = if S = “ 11”, then Y = I 0 I 1 I 2 I 3 3 Y = I 0 S 1’ S 0’ + I 1 S 1’ S 0 + I 2 S 1 S 0’ + I 3 S 1 S 0 BR 8/99 3

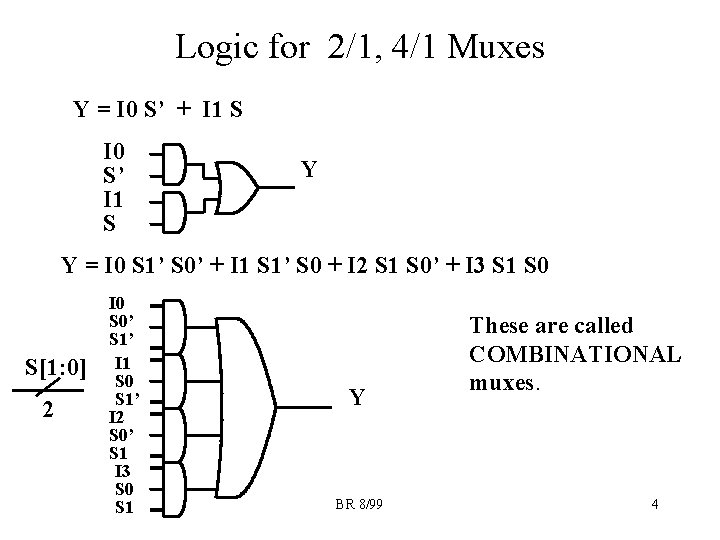
Logic for 2/1, 4/1 Muxes Y = I 0 S’ + I 1 S I 0 S’ I 1 S Y Y = I 0 S 1’ S 0’ + I 1 S 1’ S 0 + I 2 S 1 S 0’ + I 3 S 1 S 0 S[1: 0] 2 I 0 S 0’ S 1’ I 1 S 0 S 1’ I 2 S 0’ S 1 I 3 S 0 S 1 Y BR 8/99 These are called COMBINATIONAL muxes. 4

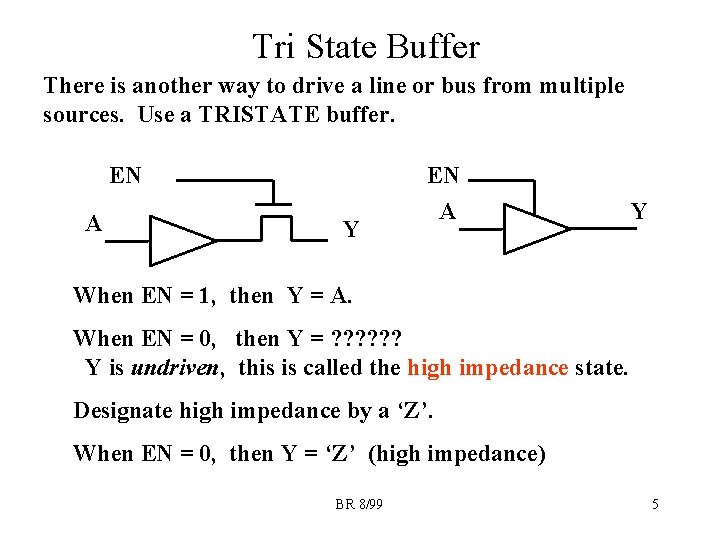
Tri State Buffer There is another way to drive a line or bus from multiple sources. Use a TRISTATE buffer. EN A Y When EN = 1, then Y = A. When EN = 0, then Y = ? ? ? Y is undriven, this is called the high impedance state. Designate high impedance by a ‘Z’. When EN = 0, then Y = ‘Z’ (high impedance) BR 8/99 5

Using Tri. State Buffers Can use tristate buffers instead of a combinational 2/1 mux ENA A Y ENB B Must make sure that ENA, ENB are not both ‘ 1’ at same time, or Y will be driven from multiple sources BR 8/99 6

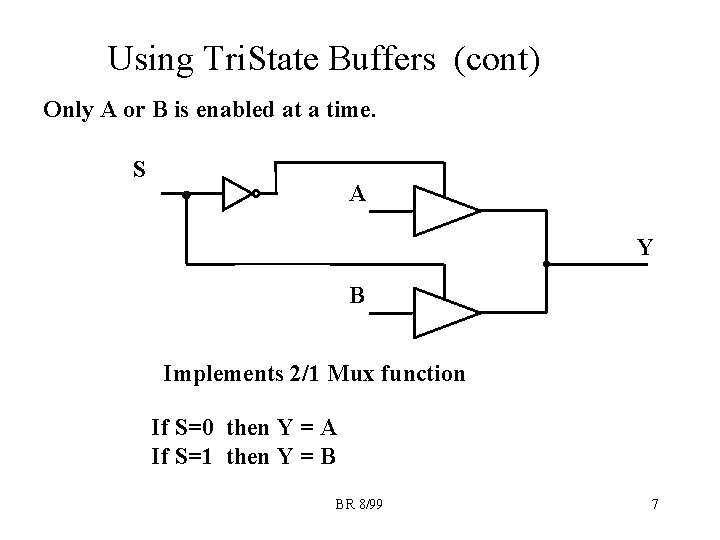
Using Tri. State Buffers (cont) Only A or B is enabled at a time. S A Y B Implements 2/1 Mux function If S=0 then Y = A If S=1 then Y = B BR 8/99 7

Using Tri. State Buffers (cont) S 0’ S 1’ A S[1: 0] 2 S 0 S 1’ S 0’ S 1 S 0 S 1 Y B Y is driven by A, B, C or D; only one source is enabled at a time. C D Implements 4/1 MUX function. BR 8/99 8

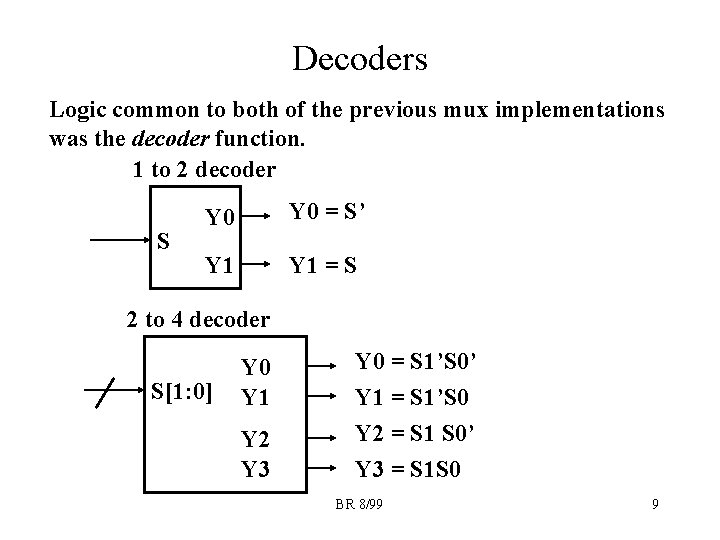
Decoders Logic common to both of the previous mux implementations was the decoder function. 1 to 2 decoder S Y 0 = S’ Y 1 = S 2 to 4 decoder S[1: 0] Y 0 Y 1 Y 2 Y 3 Y 0 = S 1’S 0’ Y 1 = S 1’S 0 Y 2 = S 1 S 0’ Y 3 = S 1 S 0 BR 8/99 9

Logic for 4/1 Combinational Mux Y 0 I 0 2 Y 1 S[1: 0] I 1 Y Y 2 I 2 Y 3 I 3 2 to 4 decoder BR 8/99 10

4/1 Mux using Decoder + TSBs Y 0 A 2 S[1: 0] Y Y 1 B Y 2 C Y 3 D 2 to 4 decoder BR 8/99 11

3 to 8 Decoder A[2: 0] Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 if A= 000 then Y 0=1 else Y 0=0; if A= 001 then Y 1=1 else Y 1=0; if A= 010 then Y 2=1 else Y 2=0; if A= 011 then Y 3=1 else Y 3=0; if A= 100 then Y 4=1 else Y 4=0; if A= 101 then Y 5=1 else Y 5=0; if A= 110 then Y 6=1 else Y 6=0; if A= 111 then Y 7=1 else Y 7=0; BR 8/99 12

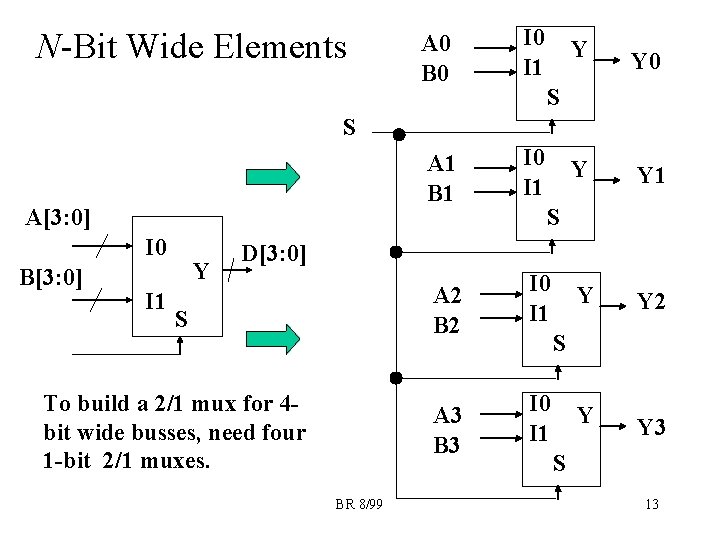
A 0 B 0 I 1 A 1 B 1 I 0 I 1 S A 2 B 2 I 0 I 1 To build a 2/1 mux for 4 bit wide busses, need four 1 -bit 2/1 muxes. A 3 B 3 I 0 I 1 N-Bit Wide Elements Y Y 0 Y Y 1 Y Y 2 Y Y 3 S S A[3: 0] I 0 B[3: 0] I 1 Y S D[3: 0] BR 8/99 S S 13

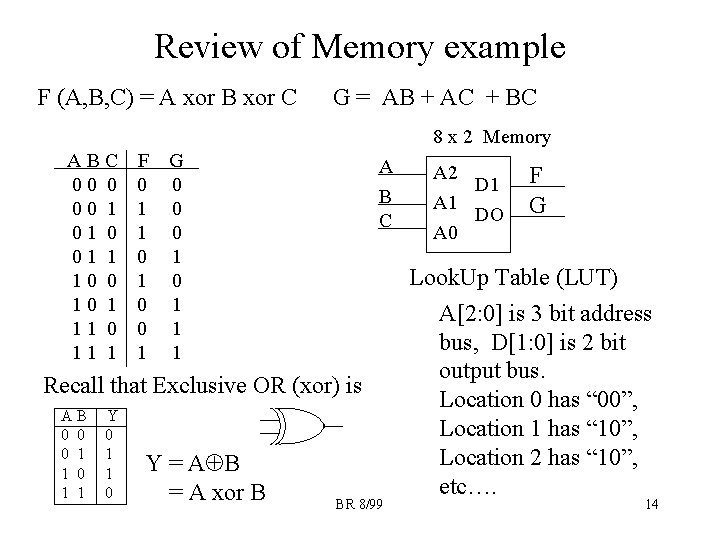
Review of Memory example F (A, B, C) = A xor B xor C G = AB + AC + BC 8 x 2 Memory ABC 00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1 F 0 1 1 0 0 1 G 0 0 0 1 1 1 A B C Recall that Exclusive OR (xor) is AB 0 0 0 1 1 Y 0 1 1 0 Y = A B = A xor B BR 8/99 A 2 D 1 A 1 DO A 0 F G Look. Up Table (LUT) A[2: 0] is 3 bit address bus, D[1: 0] is 2 bit output bus. Location 0 has “ 00”, Location 1 has “ 10”, Location 2 has “ 10”, etc…. 14

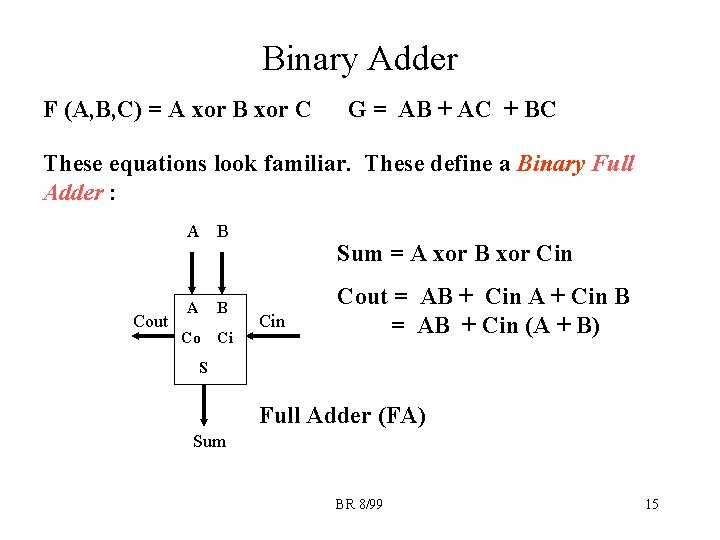
Binary Adder F (A, B, C) = A xor B xor C G = AB + AC + BC These equations look familiar. These define a Binary Full Adder : A B Cout A B Co Ci Sum = A xor B xor Cin Cout = AB + Cin A + Cin B = AB + Cin (A + B) S Full Adder (FA) Sum BR 8/99 15

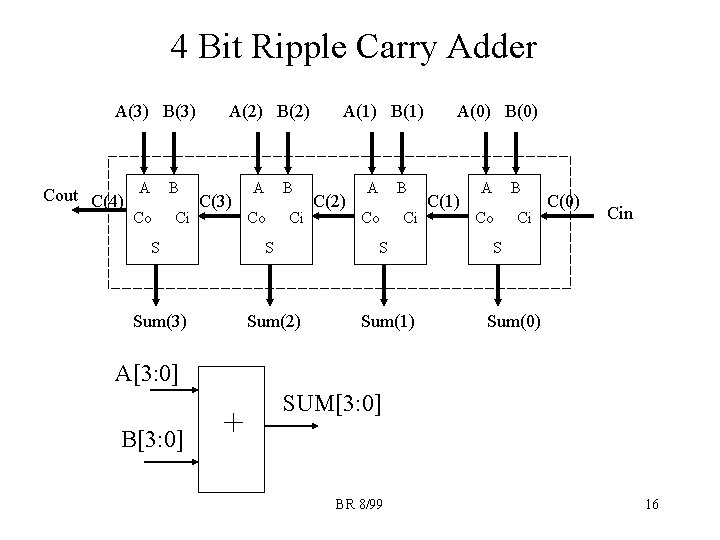
4 Bit Ripple Carry Adder A(3) B(3) Cout C(4) A B Co Ci A(2) B(2) C(3) A B Co Ci A(1) B(1) C(2) A B Co Ci S Sum(3) Sum(2) Sum(1) A(0) B(0) C(1) A B Co Ci C(0) Cin S Sum(0) A[3: 0] B[3: 0] + SUM[3: 0] BR 8/99 16

Incrementer A(3) A(2) A(1) A(0) EN xor xor Y(3) Y(2) Y(1) Y(0) A[3: 0] inc Y[3: 0] If EN = 1 then Y = A + 1 If EN = 0 then Y = A EN BR 8/99 17

What do You have to know? • Structures for Muxes, Decoders, Ripple Carry adder, Incrementer • What a tristate buffer is • How to build muxes from all combinational logic or from combinational logic + tristate buffers • Bus naming convention • How to build N-bit wide elements from 1 -bit wide elements BR 8/99 18