Column Generation 1 Outline trim loss problem different

Column Generation 1

Outline è trim loss problem èdifferent è column èthe generation trim loss problem èmaster èthe formulations problem and subproblem in column generation time constrained shortest-path problem èshortest-path subproblems for network-based problems 2

Motivation Example for Column Generation è trim-loss problem, 7 -meter steel pipes è to cut è 150 pieces of 1. 5 -meter (pipe) segments è 250 pieces of 2 -meter segments, and è 200 pieces of 4 -meter segments è loss: pipes cut and segments left after satisfying the demands è how to cut the steel pipes so as to minimize the loss? 3

Motivation Example for Column Generation è X: the total number of steel pipes used è trim loss = 7 X – (150)(1. 5) – (250)(2) – (200)(4) = 7 X-1525 è minimizing trim loss = minimizing X, the number of steel pipes used 4

Formulation 1: A Naive One Motivation Example for Column Generation è several èan formulations upper bound of pipes used: 255 è 200 pipes cut by the (0, 1, 1) pattern è 38 pipes cut by the (4, 0, 0) pattern è 17 pieces cut by the (0, 3, 0) pattern 5

Formulation 1: A Naive One Motivation Example for Column Generation è segments: 1 st type = 1. 5 meters, 2 nd type = 2 meters, and 3 rd type = 4 meters è variables è . èxij = # of type-j segments cut from pipe i = (2, 2, 0) two 1. 5 -meter segments and two 2 -meter segments from the ith pipe èe. g. , xi 6

Formulation 1: A Naive One Motivation Example for Column Generation è formulation 7

Formulation 1: A Naive One Motivation Example for Column Generation è disadvantages of Formulation 1 èmany alternate optimal solutions due to the symmetry èhard to solve 8

Formulation 2: Variables on Cut Patterns Motivation Example for Column Generation è defining variables on cut patterns è parameters èaij = # of j type segments produced by the ith cut pattern èa 1 = (a 11, a 12, a 13)T = (0, 0, 1) ètrim loss t 1 = 3 è variables: xi ith pattern = the # of steel pipes cut in the 9
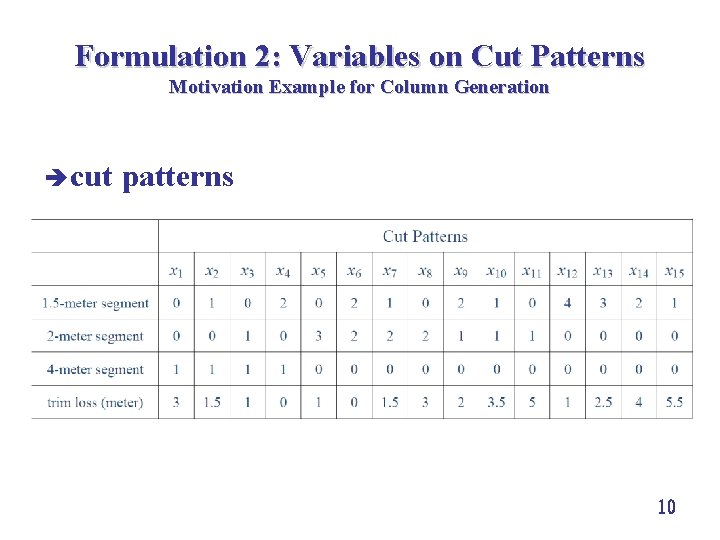
Formulation 2: Variables on Cut Patterns Motivation Example for Column Generation è cut patterns 10

Formulation 2: Variables on Cut Patterns Motivation Example for Column Generation è formulation: è question: Is it necessary to include inefficient cut patterns in this formulation? è yes è is there any formulation that uses only efficient cut patterns? 11

Formulation 3: Variables on Efficient Cut Patterns Motivation Example for Column Generation è efficient cut patterns 12

Formulation 3: Variables on Efficient Cut Patterns Motivation Example for Column Generation è formulation 13

Formulation 3: Variables on Efficient Cut Patterns Motivation Example for Column Generation è challenges èhard faced by the formulation problem, an integer program èexplosive number of variables for long pipes and multiple demands è solved by column generation èignoring the integral constraints 14

Solving the Trim Loss Problem by Column Generation è min i xi, è s. t. i aijxi bj, j = 1, 2, 3, è xi 0, i = 1, 2, 3. è = (c. B)TB-1 be the vector of dual variables è reduced cost of xi = ci - Tai = 1 - Tai è minimal reduced cost from max Tai 15

Solving the Trim Loss Problem by Column Generation è minimal reduced cost from solving the subproblem èmax è è s. t. j jaj, j ljaj L; aj Z+ {0}, i. èa knapsack problem, NP-hard, with pseudopolynomial algorithm in L 16

Solving the Trim Loss Problem by Column Generation è master problem: the problem with the columns selected èproviding è subproblem èsuggesting a new cut pattern, or optimal 17

Solving the Trim Loss Problem by Column Generation è Generic Column Generation Algorithm for the trim loss problem: è 1 Select columns for the initial basis. è 2 Solve the master problem to get è 3 Solve the knapsack subproblem for new cut pattern; stop if optimal, else go to 2 with the new cut pattern added to the master problem 18

Solving the Trim Loss Problem by Column Generation 19
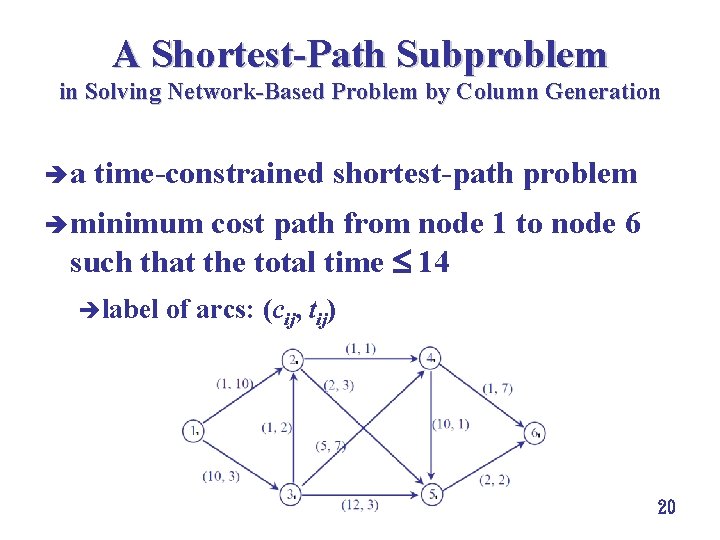
A Shortest-Path Subproblem in Solving Network-Based Problem by Column Generation èa time-constrained shortest-path problem è minimum cost path from node 1 to node 6 such that the total time 14 èlabel of arcs: (cij, tij) 20

A Time-Constrained Shortest-Path Problem è variables: xij = 1 if arc (i, j) is taken, else xij = 0 è formulation è constrained shortestpath problem, NPhard problem 21

Path-Based Formulation of a Time. Constrained Shortest-Path Problem è P: set of all paths è parameters apij = è for path 1 -2 -4 -6 to be the first path, a 112 = 1, a 124 = 1, a 146 = 1, and other a 1 ij = 0. è possible to express xij in p, where p = the “probability” that path p is taken By itself there is no guarantee p = 1 so that fractional xij may be possible. 22

A Time-Constrained Shortest-Path Problem è set of all paths for the problem 23

A Time-Constrained Shortest-Path Problem è formulation 24

A Time-Constrained Shortest-Path Problem è relaxed version: master problem solved by column generation è 1 and 0 be the dual variable of the first and the second constraints, respectively 25

A Time-Constrained Shortest-Path Problem è reduced cost of variable p 26

A Time-Constrained Shortest-Path Problem è subproblem: shortest-path problem s. t. xij {0, 1}, (i, j) A. 27

Solving the Time Constrained Shortest. Path Problem by Column Generation è Generic Column Generation Algorithm for the time constrained shortest-path problem: è 1 Start arbitrarily with a feasible path è 2 Solve the master problem to get è 3 Solve the shortest-path subproblem for new path; stop if optimal, else go to 2 with the new path added to the master problem 28
- Slides: 28