Coloracin de Grafos Planos Avance del proyecto de

Coloración de Grafos Planos Avance del proyecto de medio término Huberto Ayanegui Santiago José María Vega Ramos Enrique Ayala Franco 15 de marzo de 2001

Coloración de grafos Consiste en asignar colores a los vértices de un grafo no dirigido con la condición que para todo par de vértices adyacentes estos no sean coloreados del mismo color.

Aplicaciones

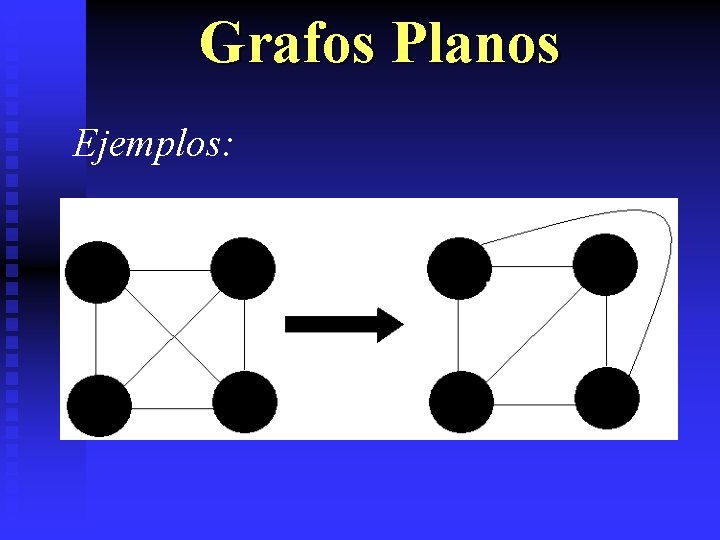
Grafos Planos Definición: Un grafo finito no dirigido se denomina plano, si puede ser dibujado sobre una superficie plana de forma que sus aristas se intersecten únicamente en los vértices.

Grafos Planos Ejemplos:

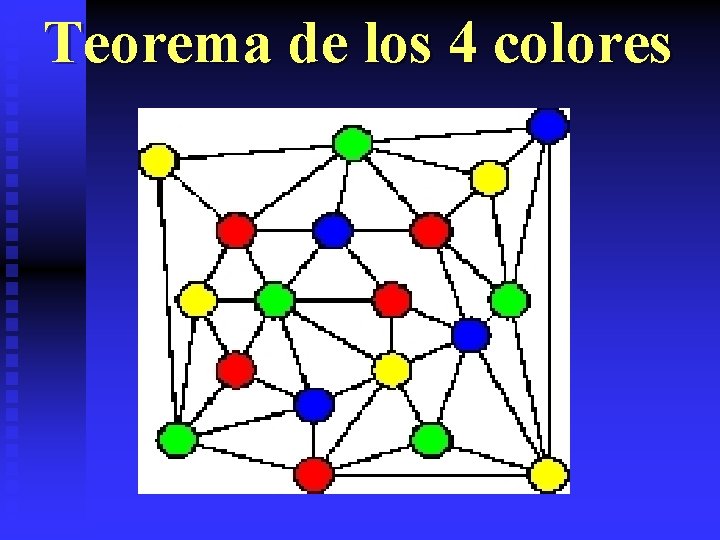
Teorema de los 4 colores Cualquier grafo plano puede ser coloreado con no más de cuatro colores, de modo que ningún par de vértices adyacentes tengan el mismo color. Francis Guthrie (1850) El teorema fue comprobado por Appel y Haken (1976)

Teorema de los 4 colores

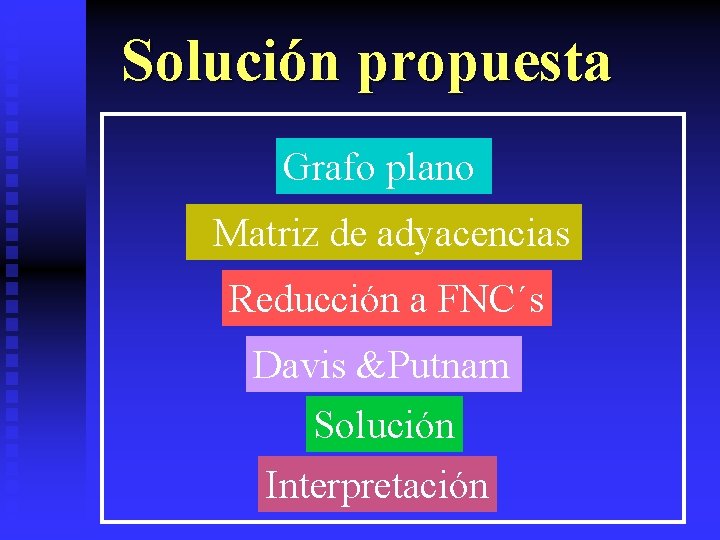
Solución propuesta Grafo plano Matriz de adyacencias Reducción a FNC´s Davis &Putnam Solución Interpretación

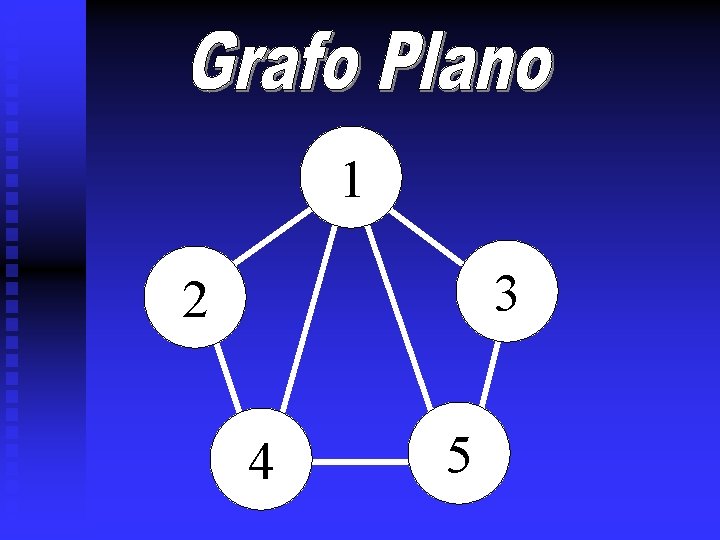
1 3 2 4 5

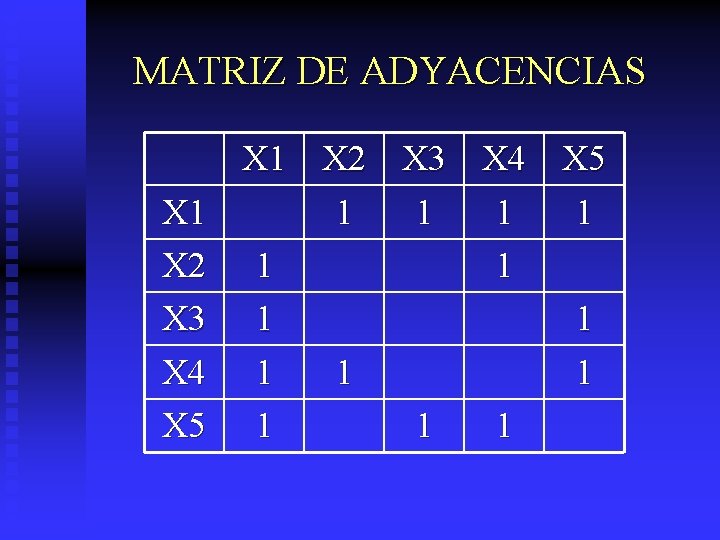
MATRIZ DE ADYACENCIAS X 1 X 2 X 3 X 4 X 5 1 1 1 1

Reducción del Grafo a Cláusulas Para el Grafo mostrado tenemos 5 vértices y 4 colores posibles para colorearlo Definiremos una proposición de la forma: Xi, j donde: i = # de vertice j = # de color

El primer paso es garantizar que cada vértice tenga al menos un color. Entonces proponemos cláusulas de esta forma: X 11 v X 12 v X 13 v X 14 X 21 v X 22 v X 23 v X 24 X 31 v X 32 v X 33 v X 34 X 41 v X 42 v X 43 v X 44 X 51 v X 52 v X 53 v X 54

El segundo paso es garantizar que cada vértice tenga un solo color. Y las cláusulas tienen esta forma: ~X 11 v ~X 12 v ~X 13 v ~X 14 ~X 21 v ~X 22 v ~X 23 v ~X 24 ~X 31 v ~X 32 v ~X 33 v ~X 34 ~X 41 v ~X 42 v ~X 43 v ~X 44 ~X 51 v ~X 52 v ~X 53 v ~X 54

El Tercer Paso es garantizar que para cada dos vértices adyacentes no tengan el mismo color. ~X 11 v ~X 21 ~X 12 v ~X 22 ~X 13 v ~X 23 ~X 14 v ~X 24 En la primera cláusula se indica que el vértice 1 adyacente al 2, no pueden tener el mismo color 1, y así susesivamente para cada par de vértices adyacentes

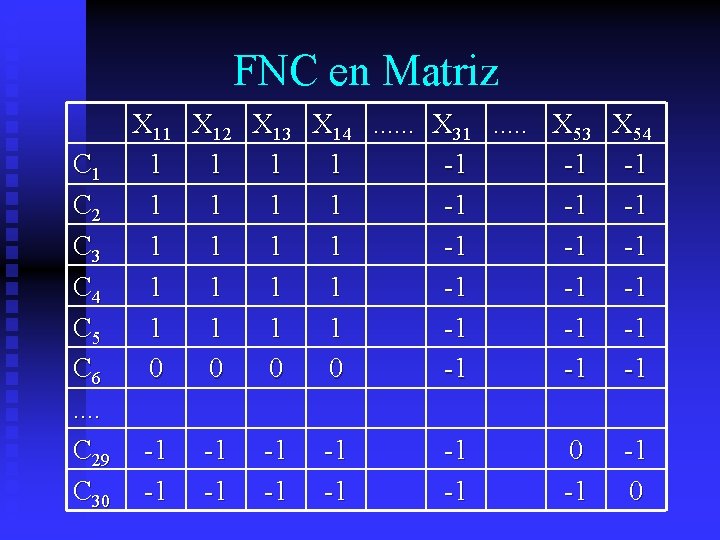
Al convertir a la Matriz FNC Consideraremos: • 0 = ~X • 1 = X • -1 = no hay asignación de verdad • -2 = proposición que fue eliminada

FNC en Matriz C 1 C 2 C 3 C 4 C 5 C 6. . C 29 C 30 X 11 X 12 X 13 X 14. . . 1 1 1 1 1 0 0 -1 -1 X 31. . . X 53 X 54 -1 -1 -1 -1 -1 0 -1 -1 0

Solución SAT function davis-putnam(in FORMULA : lista de cláusulas) reduce(FORMULA, VREDUCE) if FORMULA esta vacia then return VREDUCE; else if FORMULA contiene una clausula vacía then return "FAIL“ else begin escoge una variable V de FORMULA; VALUACION : = davis-putnam(substituye(TRUE, V, FORMULA)) if VALUACION != FAIL then return agrega(V->TRUE, VREDUCE, VALUACION); VALUACION : = davis-putnam(substituye(FALSE, V, FORMULA)) if VALUACION != FAIL then return agrega(V->FALSE, VREDUCE, VALUACION); return FAIL endif end davis-putnam

Solución SAT function substituye(TF, V, FORMULA) For cada clausula C en FORMULA do if [C contiene a V y TF = TRUE] o [C contiene a ~V y TF = FALSE] then borrar C de FORMULA else if [C contiene a V y TF = FALSE] o [C contiene a ~V y TF = TRUE] then borrar V de C endif end. For return FORMULAend_substituye

Solución SAT Procedure Reduce(in out FORMULA, VREDUCE) VREDUCE : = vacío; While exista una clausula C en FORMULA con solo una literal L IF L es una variable positiva V then FORMULA : = sustitucion(VERDADERO, V, FORMULA) VREDUCE : = cons(V-> TRUE, VREDUCE); Else IF L es la negacion de la variable V then FORMULA : = sustitucion(FALSE, V, FORMULA) VREDUCE : = cons(V-> FALSE, VREDUCE); End. IF End. While return(FORMULA)end_Reduce

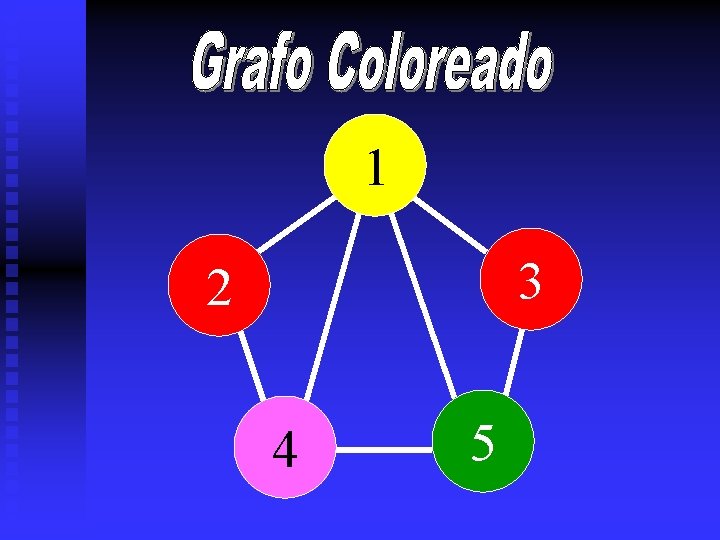
1 3 2 4 5