Collision detection Static interference tests Exacxt collision prediction

Collision detection § Static interference tests § Exacxt collision prediction § Conservative tests and acceleration techniques “Collision detection is one of the most challenging and most important problems in computer animation!” Updated 16 September 2020 Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 1

Types of animations § Camera moves in static environment § Rigid motion: Objects are rigid, they only rotate and translate § Articulated bodies: Parameterized linkage of rigid bodies – A child’s pose (forearm) is obtained from a parent’s pose (upper-arm) by an arbitrary rotation (elbow angle) and a fixed translation (length of upper-arm). § Deformations: Each shape deforms with time – Deformation may be simulated using naïve physics or computed to interpolate between two shapes (3 D morphing) § Reactive: Responds to user actions – Shape moves and deforms when approached or poked by the user All must detect collisions and adjust behavior Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 2

The collision detection problem Shapes A and B evolve (move, deform) with time. Notation for their instance at time t>0: A(t) and B(t). Find the smallest t such that A(t) B(t) . Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 3

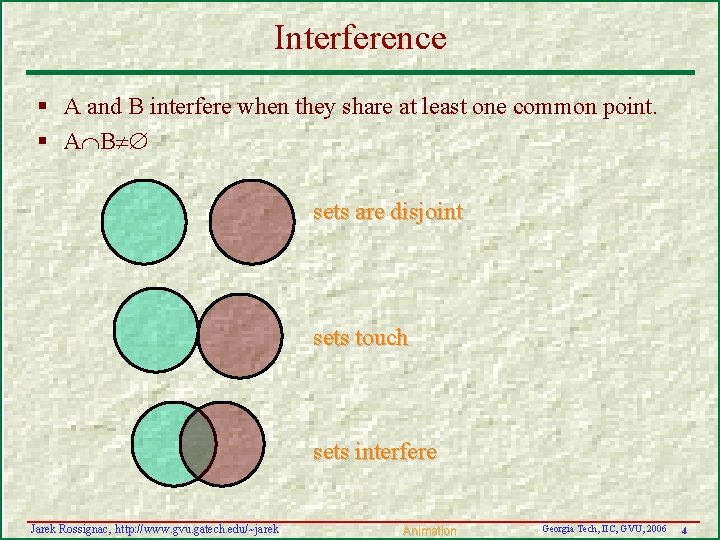
Interference § A and B interfere when they share at least one common point. § A B sets are disjoint sets touch sets interfere Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 4

Static interference tests for collision A and B evolve (move, deform) with time: A(t) and B(t). Test and then assume A(0) B(0)= t=0; repeat { if (A(t+dt) B(t+dt) ) { repeat 5 times { if (A(t+dt/2) B(t+dt/2) ) dt=dt/2; else t+=dt/2; }; return(t); }; } return(-1); } // no collision found red Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation t green Georgia Tech, IIC, GVU, 2006 5

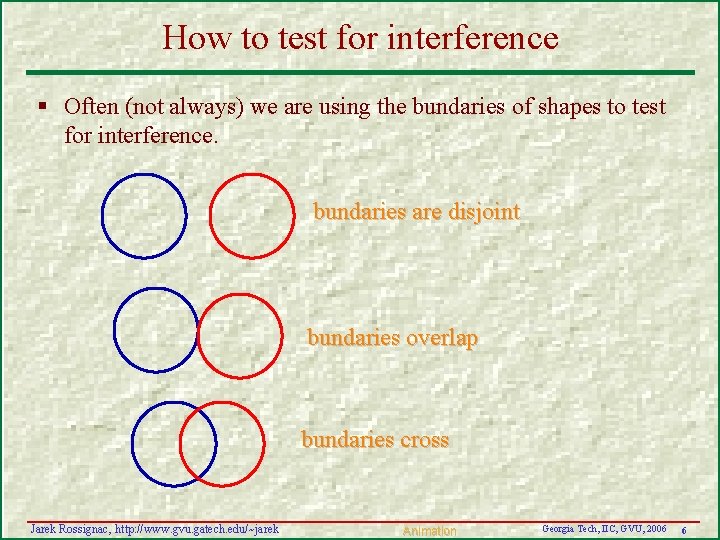
How to test for interference § Often (not always) we are using the bundaries of shapes to test for interference. bundaries are disjoint bundaries overlap bundaries cross Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 6

Testing boundaries § A and B are disjoint if and only if their boundaries are disjoint – True or false? – If true, prove or justify – If false, provide a counterexample and propose a correct test using the bundaries: • “A and B are disjoint iff their bundaries …” sets are disjoint bundaries touch bundaries overlap sets interfere Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek bundaries cross Animation Georgia Tech, IIC, GVU, 2006 7

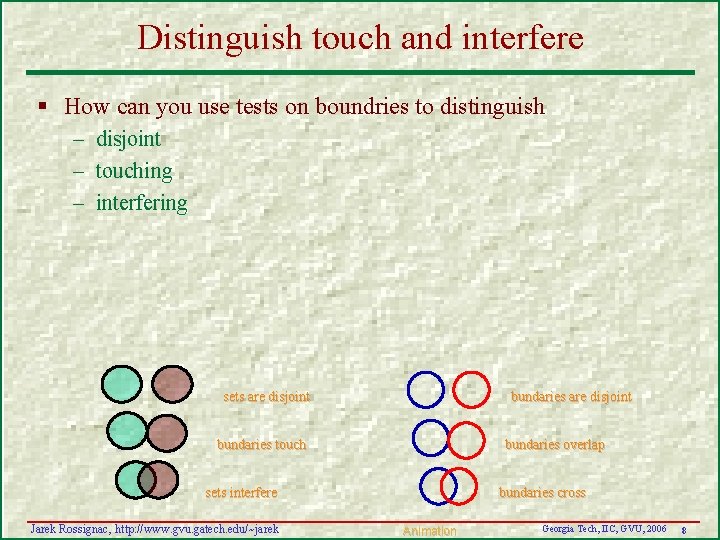
Distinguish touch and interfere § How can you use tests on boundries to distinguish – disjoint – touching – interfering sets are disjoint bundaries touch bundaries overlap sets interfere Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek bundaries cross Animation Georgia Tech, IIC, GVU, 2006 8

Detecting collisions between balls § For simplicity, we assume that objects collide when their enclosing balls collide – Compute enclosing ball of center c and radius r as follows: • c : = ( (xmin+xmax)/2, (ymin+ymax)/2, (zmin+zmax)/2 ) • r : = max (||cv||) for all vertices v of the object § Interference detection: – After each time step, check whether any pair of objects interfere – Ball(c 1, r 1) and Ball(c 2, r 2) interfere when ||c 1 c 2|| < r 1+r 2 – Need very small steps not to miss a chock § Collision prediction: – Express the relative motion of object 2 in the CS of object 1 • For motions with fixed velocities, v 1 and v 2, you get v 1 and v 2, v = v 2 – v 1. – Shrink object 2 to a point c 2 and expand object 1 to Ball(c 1, r 1+r 2) – Check whether curve swept by c 2 intersects Ball(c 1, r 1+r 2) • Constant velocity motion: find smallest time t>0 when (c 2 +tv)2=(r 1+r 2)2 Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 9

Collision between disks Assume that disk D 1=disk(C 1, r 1) will travel with constant velocity V 1. Similarly, disk D 2 =disk(C 2, r 2) will travel with constant velocity V 2. Assume that they are initially disjoint. § How would you compute the time t when they will collide? Solve ((C 2+t. V 2)–(C 1+t. V 1))2=(r 1+r 2)2 for t (C 1 C 2+t(V 2–V 1))2=(r 1+r 2)2 (V 2–V 1)2 t 2 + 2 C 1 C 2 (V 2–V 1) t + C 1 C 22 –(r 1+r 2)2 = 0 return the smallest positive value of t if one exists We can reduce this problem to the one of line/circle intersection: D 2 is stationary, D 1 moves by V 1–V 2 D 2 has radius r 1+r 2 (inflated by r 1), D 1 is a point (deflated by r 1) when will D 1 (the point) hit the inflated D 2? Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 10

Elastic shock between two disks Assume that disk D 1=disk(C 1, r) traveling with constant velocity V 1 and disk D 2 =disk(C 2, r) traveling with constant velocity V 2 have just collided. What should their velocities V 1’ and V 2’ be? (We assume that they have the same mass. ) We must exchange their normal velocities N = C 1 C 2. unit (normal direction to both at contact point) U 1 = (V 1 N) N (normal components of velocities) U 2 = (V 2 N) N V 1’= V 1 – U 1+ U 2 (cancel U 1 and add U 2) V 2’= V 2 – U 2+ U 1 ( to exchange their normal velocities) Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 11

Elastic shock with a fixed disk Assume that disk D 1=disk(C 1, r), traveling with constant velocity V, has just collided with a static disk D 2 =disk(C 2, r). What should its velocity V’ after the bounce? (We assume that D 2 has infinite mass. ) We must negate (reverse) the normal component of V N = C 1 C 2. unit (normal direction to both at contact point) U = (V N) N (normal components of V) V’= V 1 – 2 U (swap direction of U) Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 12

Elastic collision between balls § § § Tangential velocities are maintained, normal velocities are computed using (8) Masses: a and b Velocities in the normal direction: s and t before and s’ and t’ after the shock – – – – – § § Conservation of momentum: as+bt=as’+bt’ (1) Conservation of energy: as 2+bt 2=as’ 2+bt’ 2 (2) Regrouping in (1): a(s-s’)=b(t’-t) (3) Regrouping in (2) and using x 2 -y 2=(x+y)(x-y): a(s-s’)(s+s’)=b(t’-t)(t’+t) (4) Combining (3) and (4) : s+s’=t+t’ (5) Substituting t’=s+s’-t obtained from (5) in (1) yields: as+bt=as’+bs+bs’-bt (6) Reorganizing (6) : (a+b)s’=(a-b)s+2 bt (7) Reorganizing and swapping (s, a) and (t, b): s’=s+2 b(t-s)/(a+b) and t’=t+2 a(s-t)/(a+b) (8) Note that when a=b, then s’=t and t’=s (exchange of normal velocities) When a>>b: s’=s (not affected) and t’=2 s-t (reverse speed of b if a is static) s a t chock t’ s’ b Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 13

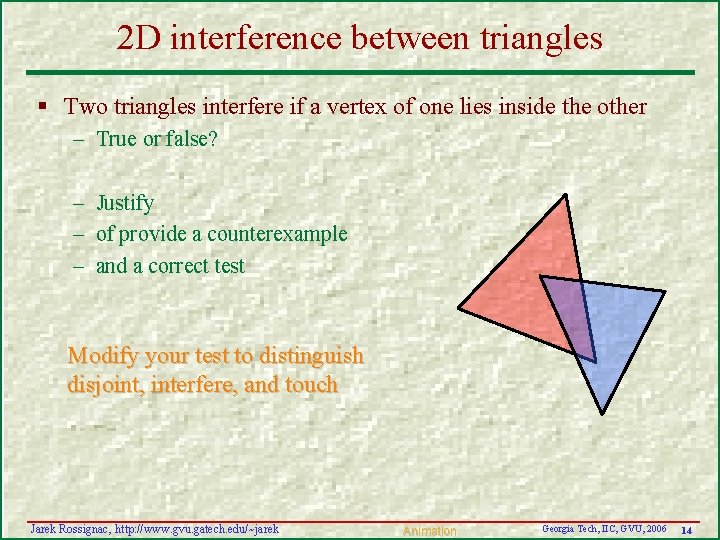
2 D interference between triangles § Two triangles interfere if a vertex of one lies inside the other – True or false? – Justify – of provide a counterexample – and a correct test Modify your test to distinguish disjoint, interfere, and touch Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 14

Test for polygon/polygon intersection in 2 D? § A and B are polygons – They are connected sets in 2 D, but may have holes § Write the high-level test for checking whether they interfere For each connected component of A do, if the first vertex of that component is in or on B, return TRUE For each connected component of B do, if the first vertex of that component is in or on A, return TRUE For each edge Ea of A do, for each edge Eb of B do, if Ea intersects Eb, return TRUE Otherwise return FALSE Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 15

Details § Point-in-polygon § Edge/edge intersection Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 16

Point-in-polygon test § Algorithm for testing whether point q is inside polygon P b a q P o in. P: =false; for each edge (a, b) of P {if (in. Triangle(q, a, b, o)) then in. P : = !in. P; return(in. P); Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 17

Point-in-triangle test in 2 D b § Is point q in tri(a, b, c) ? q c a ab. left() • aq bc. left() • bq ca. left() • cq all have the same sign Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 18

Edge/edge intersection in 2 D § Write a geometric expression that returns TRUE when edges (a, b) and (c, d) intersect ( (ab. left() • ac>0) != (ab. left() • ad>0) ) && ( (cd. left() • ca>0) != (cd. left() • cb>0) ) d b a c Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 19

Intersection between triangle meshes A and B are disjoint when the following conditions are all true – VB VA= , • Each verted of A is different from each vertex of B • Test for equality of coordinates (use distance threshold? ) – VA EB= , VB EA= , • Test whether any vertex of one lies on any edge of the other • Use Pin. E(point, edge) test in 3 D (see next slides) – VA FB= , VB FA= , • Test whether any vertex of one lies on any face of the other • Use Pin. T(point, triangle) test in 3 D (see next slides) – EA EB= , • Test whether any edge of one intersects any edge of the other • Compare edge-edge distance, EEdist(edge, edge), to threshold – EA FB= , EB FA= , § § § • Test whether any edge of one intersects any triangle of the other • Use edge-triangle intersection test, Ein. T(edge, triangle), in 3 D Why is it unnecessary to test FA FB= ? Is the last condition sufficient? How to distinguish between touch and interfere? Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 20

Pin. E(point, edge): Point-in-edge test § Pin. E(p, edge(a, b)) : = ||ab ap||< ||ab|| AND ab • ap>0 AND ba • bp>0 – Let q be the projection of p onto the line through a and b – The distance ||pq|| from p to q is ||ab ap|| / ||ab|| • It needs to be less than the threshold – We also want q to be inside edge(a, b) p • ab • ap>0 AND ba • bp>0 a b q p a b q Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 21

Pin. T(point, triangle): Point-in-triangle test Pin. T(p, tri(a, b, c)) : = (n • ap)< ||n|| AND Same. Sign((n ab) • ap, (n bc) • bp, (n ca) • cp)), where n=ab ac Let q be the projection of p onto the plane through a, b and c b n=ab ac is orthogonal to the plane though a, b, c p The distance ||pq|| is (n • ap)/||n|| a It needs to be less than the threshold c We also want q to be inside triangle(a, b, c) Same. Sign((n ab) • ap , (n bc) • bp , (n ca) • cp ) b c Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation a q p Georgia Tech, IIC, GVU, 2006 22

Eint. E(edge, edge): Edge-edge intersection § Eint. E(edge(a, b), edge(c, d)): = n • ac< ||n|| && Same. Sign((ab n) • ac, (ab n) • da) && Same. Sign((cd n) • ca, (cd n) • cb) With n=ab ac being the common normal to both lines Let p and q be the points that minimize the distance between the two lines. The distance between the lines is ||pq|| = n • ac / ||n|| But we also want to ensure that it occurs inside the edges • Same. Sign((ab n) • ac, (ab n) • da) AND Same. Sign((cd n) • ca, (cd n) • cb) – Points c and d must be on opposite sides of plane through a with normal n – Points a and b must be on opposite sides of plane through a with normal n d q a p b c Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 23

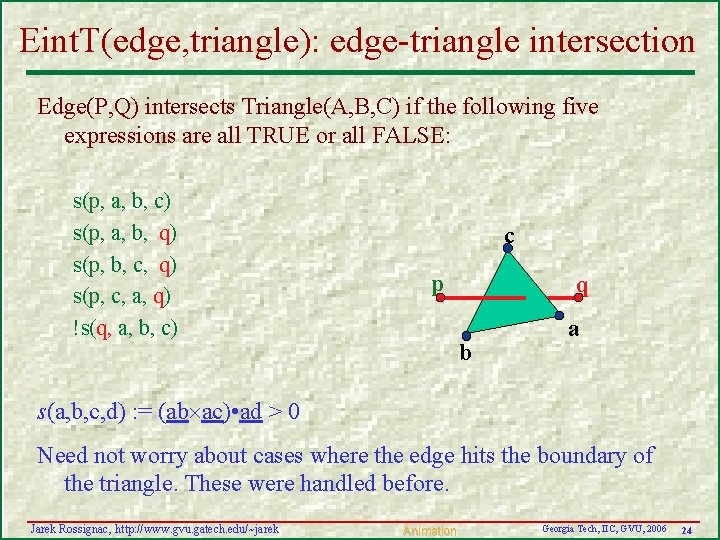
Eint. T(edge, triangle): edge-triangle intersection Edge(P, Q) intersects Triangle(A, B, C) if the following five expressions are all TRUE or all FALSE: s(p, a, b, c) s(p, a, b, q) s(p, b, c, q) s(p, c, a, q) !s(q, a, b, c) c p q b a s(a, b, c, d) : = (ab ac) • ad > 0 Need not worry about cases where the edge hits the boundary of the triangle. These were handled before. Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 24

Interfering solids Assume that two triangle meshes A and B are disjoint, what else do you need to test to be able to conclude that the solids they bound are disjoint? Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 25

Summary on static interference tests Simulate motion/deformation step-by-step and test for static interference between objects at each key-frame – Stop when interference is detected – Search for correct collision time • Binary split of current time-step • Static interference detection is difficult to code and slow O(n 2) static interference detections between pairs of objects – Each checks whether an edge of one stabs the face of another – Expensive (O(n 2) per time step) Can easily miss collisions t 1 Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation t 2 t 3 Georgia Tech, IIC, GVU, 2006 26

Interference tests are not safe § Testing collision via interfrence tests at discrete time steps is not safe. found collision Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek missed collision Animation Georgia Tech, IIC, GVU, 2006 27

Interference prediction Instead of testing interferences for discrete time steps, it would be better to predict when the collision will happen, if at all. Do not attempt this at home for complex animations. This is only practical for simple motions of rigid objects. We address it only for rigid objects Express motion of one in the CS of the other Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 28

Colliding polyhedra § Assume solids A and B are initially disjoint polyhedra § Assume B is static and A moves by rigid-body motion M(t) § At time t when first collision occurs: – a vertex of A@M(t) is in a face of B or – a vertex of B is in a face of A@M(t) or – an edge of A@M(t) intersect an edge of B § Use these conditions to formulate equations in t § Find roots and test whether they correspond to intersections From Boyse’ 79 Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 29

Case of costant velocity § Assume A moves with constant velocity M(t)=tv and B is fixed – If both move, compute collision in local coordinate system of B c § Collision may occur between a – A vertex p of A and (the closure of) a triangle T of B H • Intersect Ray(p, v) with T t – The closure of a triangle T of A with a vertex p of B • Intersect Ray(p, -v) with T b v p – An edge (a, b) of A with an edge (c, d) of B • Check when the volume of tetrahedron (a+tv, b+tv, c, d) becomes zero • Make sure that, at that time, the two edges intersect d b v a Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 c 30

Vertex hits triangle We will use: boolean s(u, v, v) {return (u v) • w > 0 } A vertex starting at P traveling with velocity V follows Ray(p, v) 1) Test whether Ray(p, v) hits triangle(a, b, c) – Test whether triangle (a, b, c) is front facing: s(pa, pb, pc) – If not, swap a and b (in the next test) – Test whether triangle is stabbed by ray b c h s(pa, pb, v) && s(pb, pc, v) && s(pc, pa, v) • t If so, compute collision time and place – Collision time v t = (ab ac) • pa / (ab ac) • v 1) Collision point p h = p + t. V Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek a Animation Georgia Tech, IIC, GVU, 2006 31

Edge/edge collision An edge (a, b) of A with an edge (c, d) of B – The volume of tetrahedron (a+tv, b+tv, c, d) is zero • solve (cd (ca+tv)) (cb+tv)=0 for t • t = (ca cd) cb / (ab cd) v – Make sure that, at time t, the two edges intersect d b v a c solve (cd (ca+tv)) (cb+tv)=0 for t (cd (ca+tv)) cb + (cd (ca+tv)) tv)=0 (cd ca+t(cd v)) cb + (cd ca+t(cd v)) tv)=0 (cd ca) cb +t(cd v) cb + (cd ca) tv +t 2(cd v) v = 0 (cd ca) cb +t(cd v) cb + (cd ca) tv = 0, because (cd v) v = 0 t = (ca cd) cb / ((cd v) cb - (cd v) ca) t = (ca cd) cb / (ab cd) v Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 32

General motions (with B. M. Kim) For each pair of objects A and B do Approximate relative motion by polyscrew • Insert intermediate poses as needed adaptively For each screw motion segment do Use conservative rejection test to identify collision-free situations If collision may not be discarded, then do • For each vertex of A(resp. B) and each triangle of B (resp. A) do – If collision cannot be discarded using bounds – Then find time of first collision (if one occurs) • For each edge of B and each edge of A do – If collision cannot be discarded using bounds – Then find time of first collision (if one occurs) • Stop if collision found and report the smallest time of first collision Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 33

Conservative tests A collision test T is either correct or wrong T is conservative when: collision T boolean T {return(false); } is conservative by not accurate We want conservative tests that are rarelywrong § § § Separating half-space Distances Space partition Swept regions Voxels Hardware Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 34

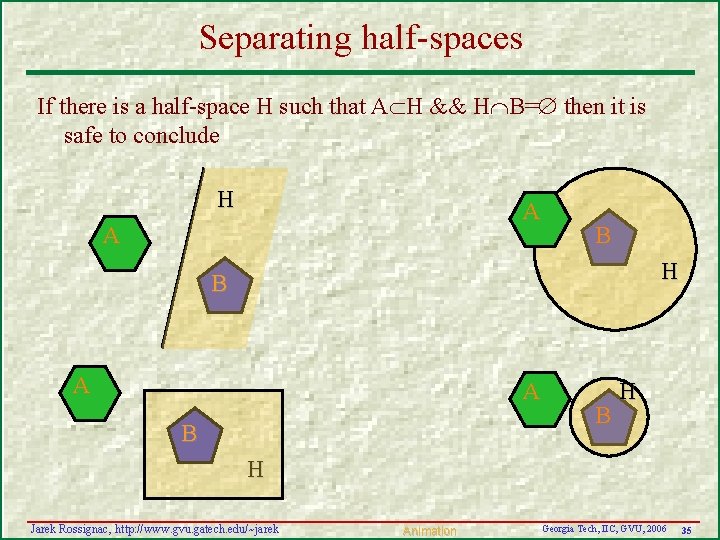
Separating half-spaces If there is a half-space H such that A H && H B= then it is safe to conclude H A A B H B A A B B H H Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 35

Bounding balls § Tight enclosing balls are – cheap to compute (center of min/max box, radius min distance) – trivial to rotate – lead to inexpensive interference test no collision possible collision Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 36

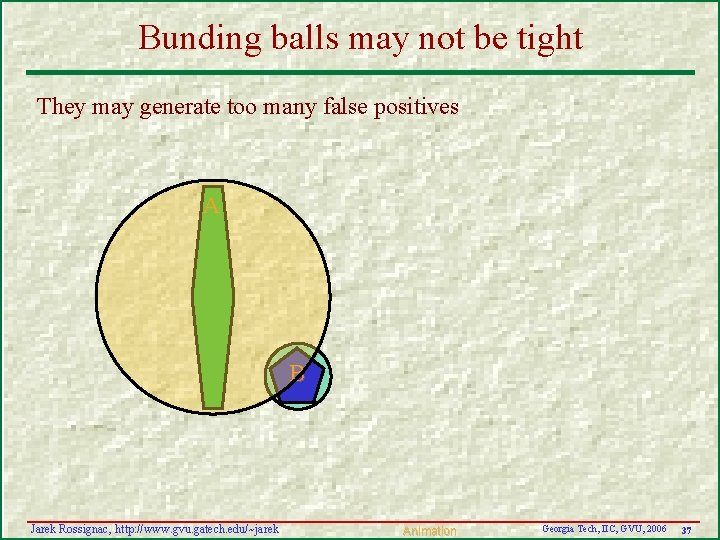
Bunding balls may not be tight They may generate too many false positives A B Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 37

Linear half-spaces may be better Find the normal NH, such that the convex hulls of the projections of the vertices of A and of the vertices of B onto some line parallel to NH are disjoint Candidates for NH : A • principal axes, NH H B • diagonal axes, • normals to faces of A and B, • vector between centers, • cross-products of edge tangents (one of A , one of B). Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 38

Generalization Static interference detections are not safe Collision predition is too hard for general motions or when the objects evolve So, what should we do? Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 39

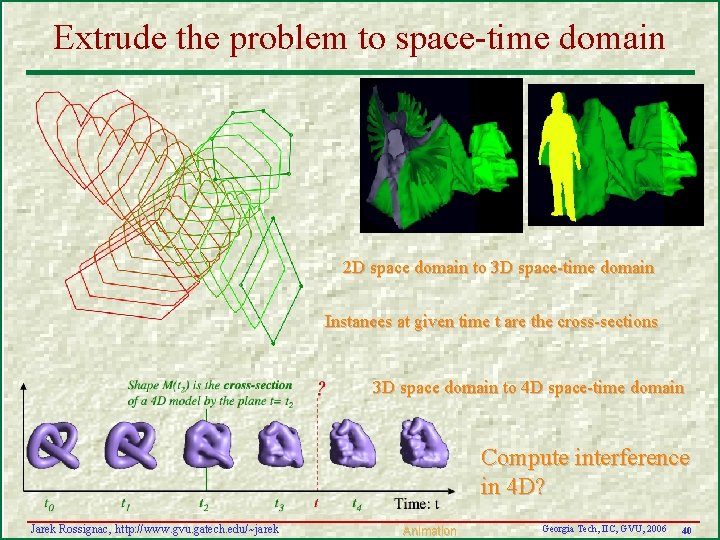
Extrude the problem to space-time domain 2 D space domain to 3 D space-time domain Instances at given time t are the cross-sections 3 D space domain to 4 D space-time domain Compute interference in 4 D? Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 40

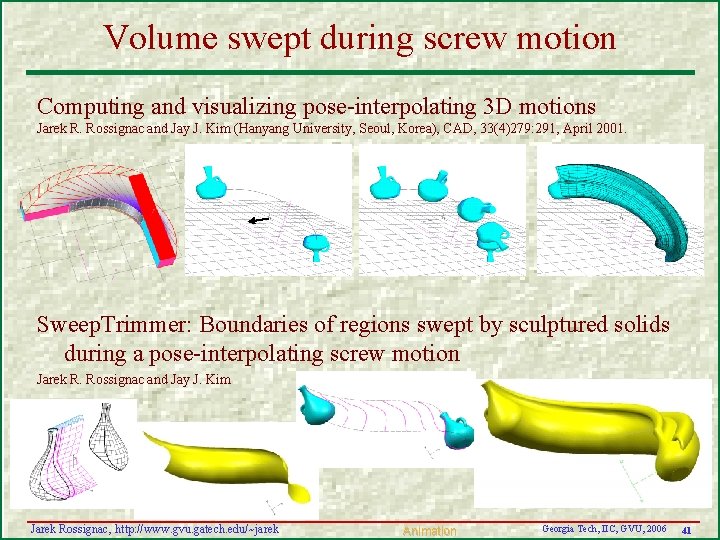
Volume swept during screw motion Computing and visualizing pose-interpolating 3 D motions Jarek R. Rossignac and Jay J. Kim (Hanyang University, Seoul, Korea), CAD, 33(4)279: 291, April 2001. Sweep. Trimmer: Boundaries of regions swept by sculptured solids during a pose-interpolating screw motion Jarek R. Rossignac and Jay J. Kim Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 41

Using sweeps § If the volumes swept by the two objects during a short time interval T do not interere, then it is save to conclude that the objects do not collide during T. § The swept volume is the projection of the 4 D animation onto the 3 D space. Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 42

How to generate swept volume bounds? § Sweeps of enclosing ball (cylinder, torus, helix) § Minkowski morph (of bunding box) Jarek Rossignac, http: //www. gvu. gatech. edu/~jarek Animation Georgia Tech, IIC, GVU, 2006 43