Collimation of Beam Halo for Compton Spectrum Diagnostics

Collimation of Beam Halo for Compton Spectrum Diagnostics after the Interaction Point of ATF 2 Shan Liu, Philip Bambade, Sha Bai, Dou Wang FJPPL – FKPPL ATF 2 workshop, LAL, 11 February, 2013

Outlines ➢ Introduction ➢ Halo Generator ➢ Mad-X Simulation Results ➢ Halo Distribution with Small Energy Spread ➢ Vertical Collimation of Halo ● Vertical Halo Loss at BDUMP ● Vertical Collimation at QD 10 ➢ Halo Distribution with Large Energy Spread ➢ Horizontal Collimation of Halo ● Horizontal Collimation at QF 1 X ● Horizontal Collimation at QF 6 X ➢ Conclusions & Issues 2

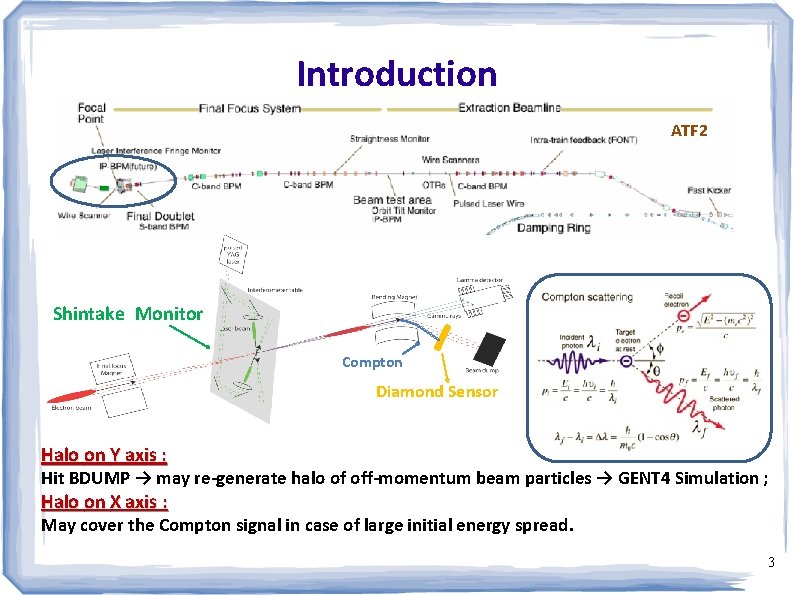
Introduction ATF 2 Shintake Monitor Compton Diamond Sensor Halo on Y axis : Hit BDUMP → may re-generate halo of off-momentum beam particles → GENT 4 Simulation ; Halo on X axis : May cover the Compton signal in case of large initial energy spread. 3

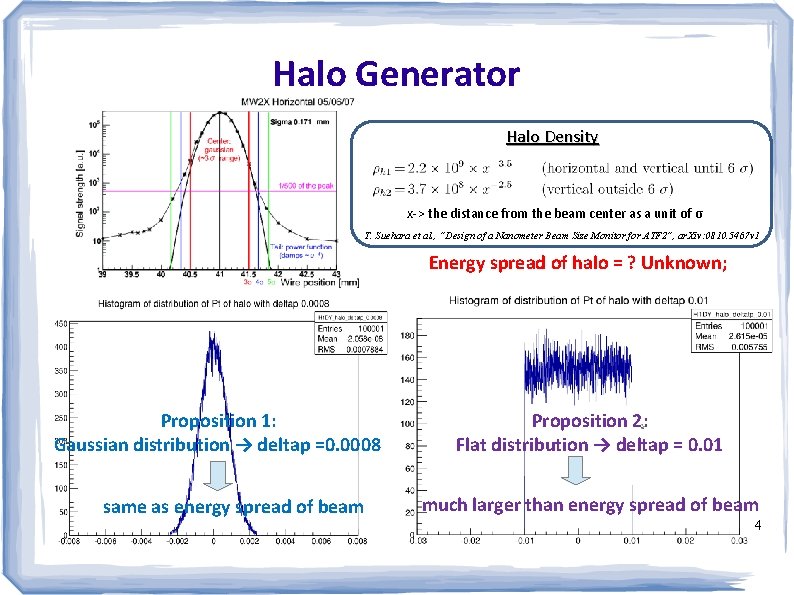
Halo Generator Halo Density x-> the distance from the beam center as a unit of σ T. Suehara et al. , “Design of a Nanometer Beam Size Monitor for ATF 2”, ar. Xiv: 0810. 5467 v 1 Energy spread of halo = ? Unknown; Proposition 1: Gaussian distribution → deltap =0. 0008 same as energy spread of beam Proposition 2: Flat distribution → deltap = 0. 01 much larger than energy spread of beam 4

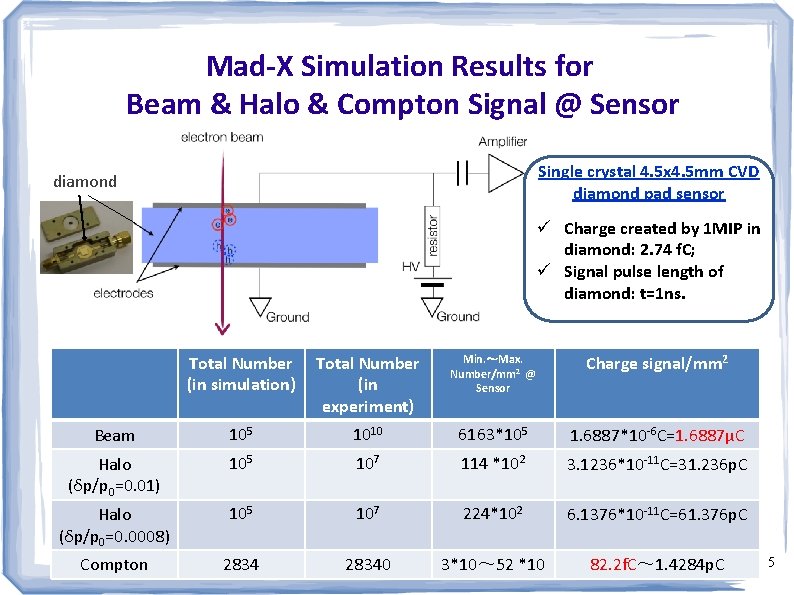
Mad-X Simulation Results for Beam & Halo & Compton Signal @ Sensor Single crystal 4. 5 x 4. 5 mm CVD diamond pad sensor diamond ü Charge created by 1 MIP in diamond: 2. 74 f. C; ü Signal pulse length of diamond: t=1 ns. Total Number (in simulation) Total Number (in experiment) Min. ～Max. Number/mm 2 @ Sensor Charge signal/mm 2 Beam 105 1010 6163*105 1. 6887*10 -6 C=1. 6887μC Halo (δp/p 0=0. 01) 105 107 114 *102 3. 1236*10 -11 C=31. 236 p. C Halo (δp/p 0=0. 0008) 105 107 224*102 6. 1376*10 -11 C=61. 376 p. C Compton 28340 3*10～ 52 *10 82. 2 f. C～ 1. 4284 p. C 5

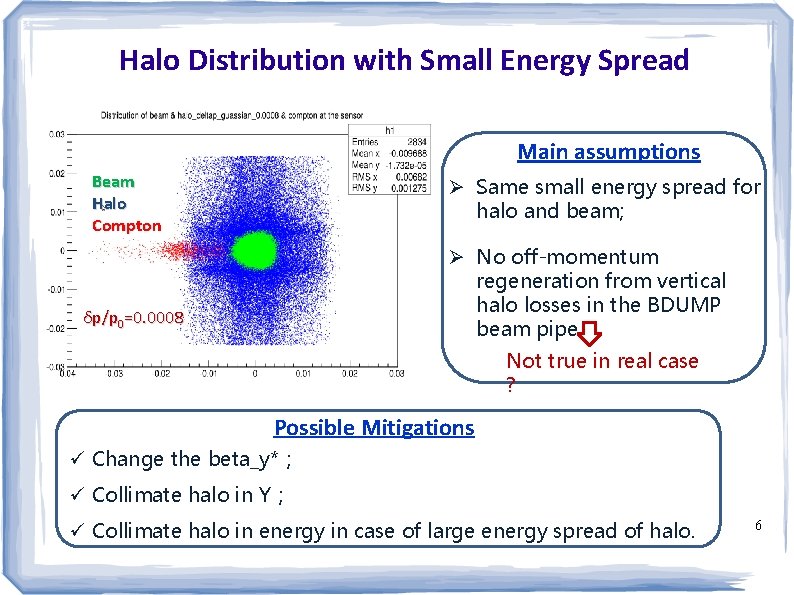
Halo Distribution with Small Energy Spread Main assumptions Beam Halo Compton Ø Same small energy spread for halo and beam; Ø No off-momentum regeneration from vertical halo losses in the BDUMP beam pipe. δp/p 0=0. 0008 Not true in real case ? Possible Mitigations ü Change the beta_y*； ü Collimate halo in Y； ü Collimate halo in energy in case of large energy spread of halo. 6

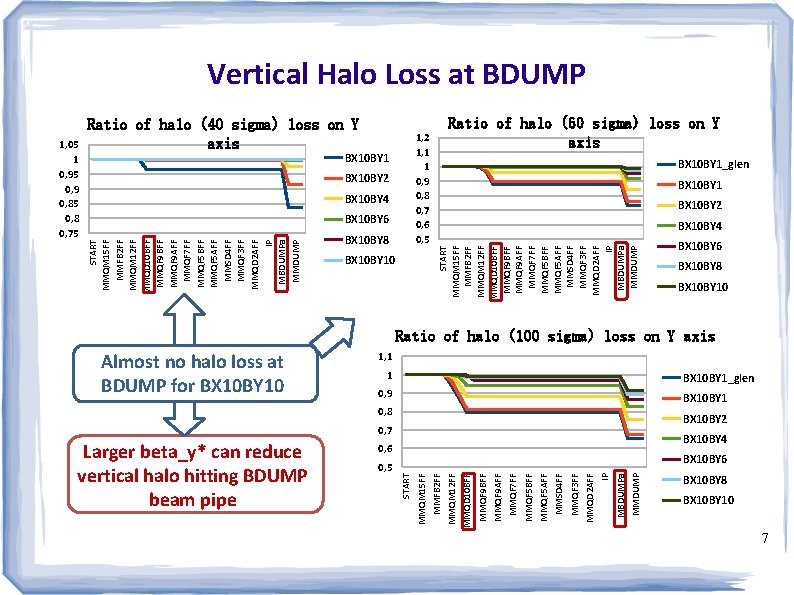
Vertical Halo Loss at BDUMP BX 10 BY 2 BX 10 BY 4 BX 10 BY 6 BX 10 BY 8 BX 10 BY 10 Ratio of halo (60 sigma) loss on Y axis BX 10 BY 1_glen BX 10 BY 1 BX 10 BY 2 BX 10 BY 4 START MMQM 15 FF MMFB 2 FF MMQM 12 FF MMQD 10 BFF MMQF 9 AFF MMQF 7 FF MMQF 5 BFF MMQF 5 AFF MMSD 4 FF MMQF 3 FF MMQD 2 AFF IP MBDUMPa MMDUMP 1, 2 1, 1 1 0, 9 0, 8 0, 7 0, 6 0, 5 BX 10 BY 1 START MMQM 15 FF MMFB 2 FF MMQM 12 FF MMQD 10 BFF MMQF 9 AFF MMQF 7 FF MMQF 5 BFF MMQF 5 AFF MMSD 4 FF MMQF 3 FF MMQD 2 AFF IP MBDUMPa MMDUMP 1, 05 1 0, 95 0, 9 0, 85 0, 8 0, 75 Ratio of halo (40 sigma) loss on Y axis BX 10 BY 6 BX 10 BY 8 BX 10 BY 10 Ratio of halo (100 sigma) loss on Y axis Almost no halo loss at BDUMP for BX 10 BY 10 1, 1 1 BX 10 BY 1_glen 0, 9 BX 10 BY 1 0, 8 BX 10 BY 2 0, 7 MMDUMP IP MBDUMPa MMQD 2 AFF MMQF 3 FF MMSD 4 FF MMQF 5 AFF MMQF 7 FF MMQF 5 BFF MMQF 9 AFF MMQF 9 BFF MMQD 10 BFF MMQM 12 FF MMFB 2 FF BX 10 BY 6 MMQM 15 FF 0, 5 START Larger beta_y* can reduce vertical halo hitting BDUMP beam pipe BX 10 BY 4 0, 6 BX 10 BY 8 BX 10 BY 10 7

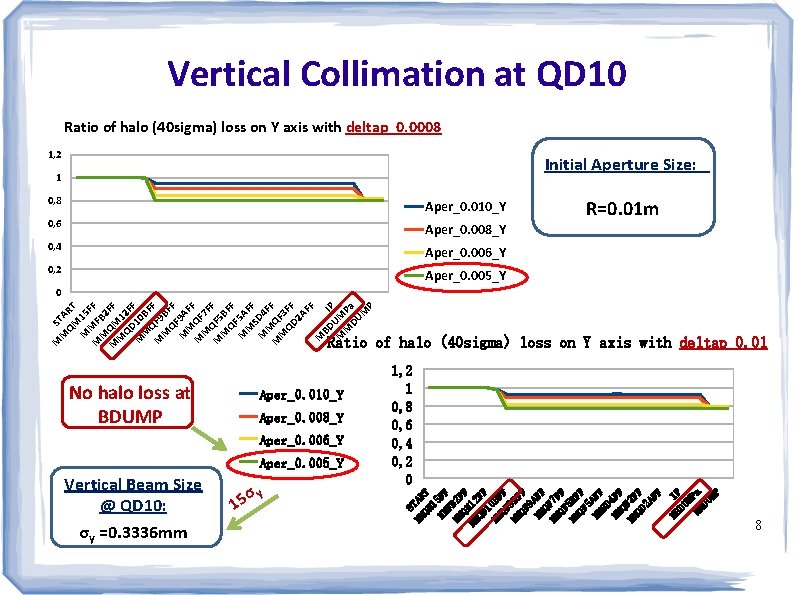
Vertical Collimation at QD 10 Ratio of halo (40 sigma) loss on Y axis with deltap_0. 0008 1, 2 Initial Aperture Size: 1 0, 8 Aper_0. 010_Y 0, 6 Aper_0. 008_Y 0, 4 Aper_0. 006_Y 0, 2 Aper_0. 005_Y R=0. 01 m M ST M A QM RT M 15 F M MF F M B 2 M QM FF M 12 QD F M 10 F M BF Q M F 9 F M BF QF F M 9 A M F M QF F M 7 F Q M F 5 F M BF QF F M 5 A M FF S M D 4 M F M QF F M 3 QD FF 2 A FF M BD IP M UM M Pa DU M P 0 Ratio of halo (40 sigma) loss on Y axis with deltap_0. 01 Aper_0. 010_Y Aper_0. 008_Y Aper_0. 006_Y Aper_0. 005_Y Vertical Beam Size @ QD 10: σy =0. 3336 mm σy 15 S MM TAR QM T 1 MM 5 FF F MM B 2 F Q F MM M 12 QD FF 1 MM 0 BF QF F MM 9 BF QF F 9 MM AFF Q MM F 7 F QF F MM 5 BF QF F 5 MM AFF SD MM 4 FF Q MM F 3 F QD F 2 A FF MB IP DU M MM Pa DU MP No halo loss at BDUMP 1, 2 1 0, 8 0, 6 0, 4 0, 2 0 8

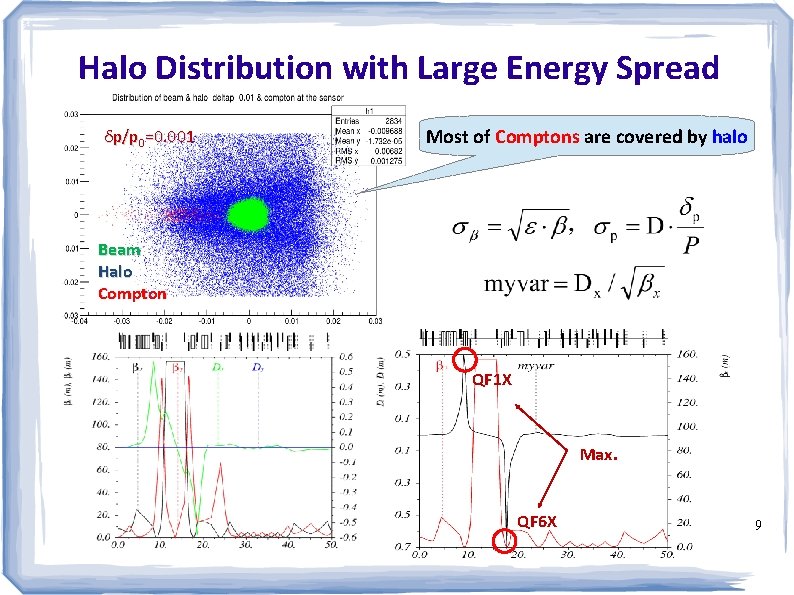
Halo Distribution with Large Energy Spread δp/p 0=0. 001 Most of Comptons are covered by halo Beam Halo Compton QF 1 X Max. QF 6 X 9

Horizontal Collimation at QF 1 X Initial Aperture Size: Energy Spread: R=0. 016 m Flat deltap= 0. 01 R=0. 003 m Compton still covered by halo 10

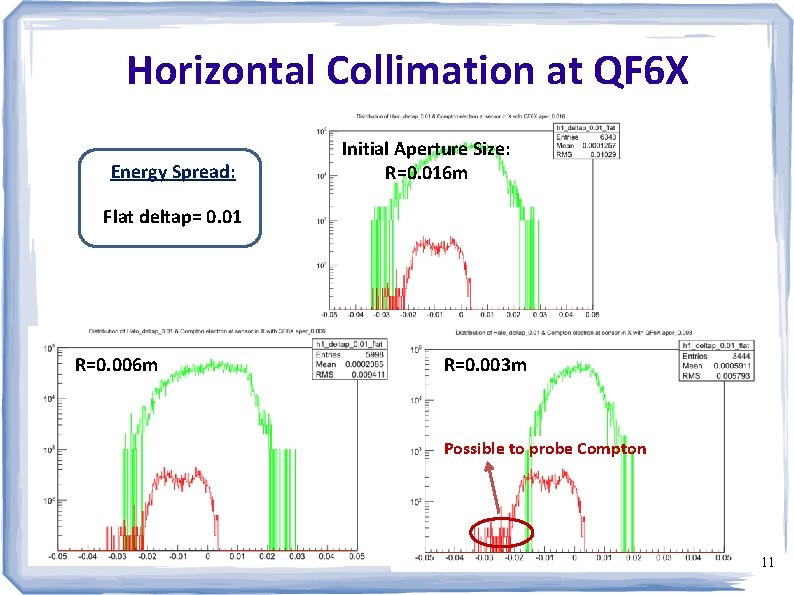
Horizontal Collimation at QF 6 X Energy Spread: Initial Aperture Size: R=0. 016 m Flat deltap= 0. 01 R=0. 006 m R=0. 003 m Possible to probe Compton 11

Horizontal Collimation at QF 6 X Initial Aperture Size: R=0. 016 m Energy Spread: Gaussian deltap= 0. 01 R=0. 005 m R=0. 003 m Enough to probe Compton? 12

Conclusions ● ● We probably need to cut the beam halo signal to probe the Compton spectrum; We can investigate halo propagating model by configuring BX & BY and by measuring the beam halo using diamond sensor; For Y axis collimation we need to change the aperture size at QD 10 BFF from 0. 01 m to 0. 005 m to avoid second generation particle from BDUMP; For X axis collimation we need to change the aperture size at QF 6 X from 0. 016 m to 0. 005 m (with deltap_gaussian=0. 01) or to 0. 003 m (with deltap_flat=0. 01) to diagnostic the Compton signal apart from the beam halo. 13

Issues ● ● How tightly can we collimate without impacting the beam emittance too much ? → Design a collimator with a special shape to minimize wakefield emittance growth effects? How large is really the energy spread of the halo and what is the distribution ? Do we really have a large re-generated halo from off-momentum beam particles induced by soft photon emissions when halo hits the beam pipe in BDUMP ? …. . 14

Thank You For Your Attention !

Backup Slides

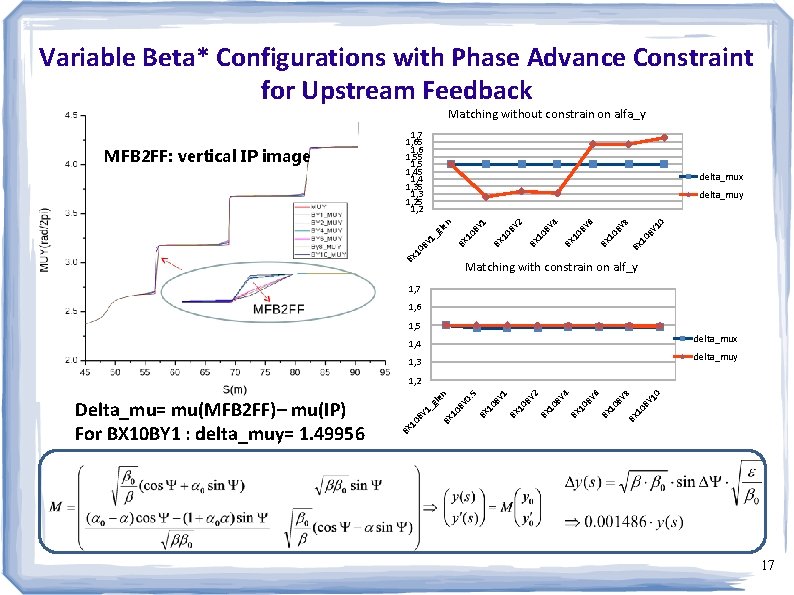
Variable Beta* Configurations with Phase Advance Constraint for Upstream Feedback Matching without constrain on alfa_y delta_mux 10 8 10 10 BY BY 6 BX BX BX 10 BY 4 BX 10 BY 2 BX 10 BY 10 BX 1_ gle BY BX 10 BY 1 delta_muy n MFB 2 FF: vertical IP image 1, 7 1, 65 1, 6 1, 55 1, 45 1, 4 1, 35 1, 3 1, 25 1, 2 Matching with constrain on alf_y 1, 7 1, 6 1, 5 delta_mux 1, 4 delta_muy 1, 3 BY 10 8 BX 10 BY 6 BX 10 BY 4 BY 2 BX 10 BY 1 BX 10 BY 5 0. 10 BY BX gle BY 1_ BX 10 Delta_mu= mu(MFB 2 FF)– mu(IP) For BX 10 BY 1 : delta_muy= 1. 49956 n 1, 2 17

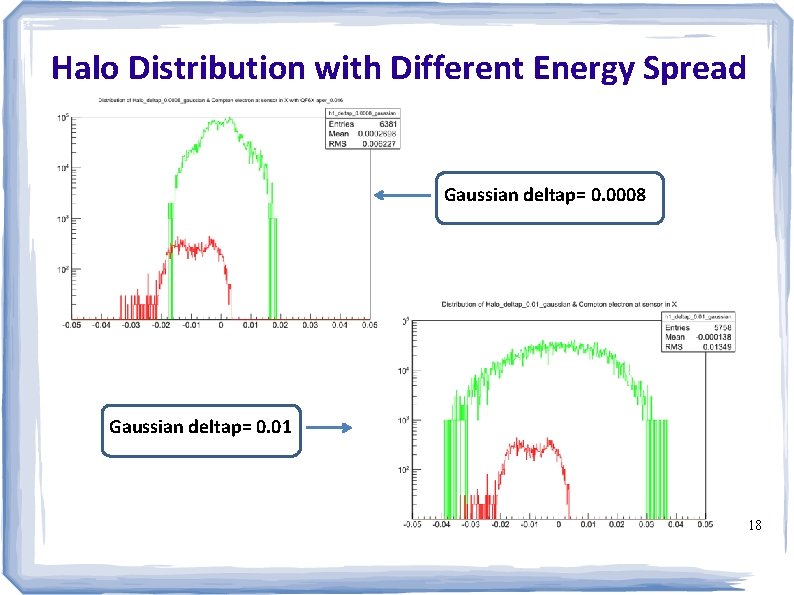
Halo Distribution with Different Energy Spread Gaussian deltap= 0. 0008 Gaussian deltap= 0. 01 18