College and Engineering Physics Vectors TOC Definitions Examples

College and Engineering Physics Vectors TOC Definitions Examples of a Vector and a Scalar More Definitions Components, Magnitude and Direction Unit Vectors and Vector Notation Vector Math (Addition, Subtraction, Multiplication) Drawing a Vector Graphical Vector Math Symmetry Sample Problems 1

College and Engineering Physics Vectors Here are some helpful definitions. TOC Magnitude: The amount of a quantity represented by a vector or scalar. Direction: The angle of a vector measured from the positive x-axis going counterclockwise. Scalar: A physical quantity that has no dependence on direction. Vector: A physical quantity that depends on direction. Units: A standard quantity used to determine the magnitude of a vector or value of a scalar. 2

College and Engineering Physics Vectors This is an example of a Vector TOC There are three representations of a vector. Change Wind Speed 1. Real life: the actual quantity that the vector represents. 2. Mathematical: a number, with units and a direction. 3. Graphical: an arrow which has a length proportional to the magnitude and a direction the same as the vector. Real Life Change Wind Direction Graphical Representation N Mathematical Representation Magnitude 24 18 12 6 w e Southeast Northwest Northeast Direction Southwest 3 Units mph s

College and Engineering Physics Vectors This is an example of a scalar. TOC There are three representations of a scalar as well Change Temperature 1. Real life: the actual quantity that the vector represents. 2. Mathematical: a number, with units and NO direction. 3. Graphical: a point on a Real Life graph. Mathematical Representation 4 Magnitude 100 75 50 25 0 Direction none Units degrees C Graphical Representation Degrees C

College and Engineering Physics Vectors More Definitions TOC Component: The projection of a vector along a particular coordinate axis. Dot Product: The product of two vectors the result of which is a scalar. Cross Product: The product of two vectors the result of which is another vector. Right-Hand Rule: The rule which gives the direction of a cross-product. 5

College and Engineering Physics Vectors To convert from magnitude/direction to components, we use two equations. TOC y-axis *Note: In order for the equations to work, θ MUST be measured from the positive x-axis going counterclockwise! (magnitude) Ay A (y-component) (the vector) θ(angle*) 6 Ax (x-component) x-axis

College and Engineering Physics Vectors Here is an example. TOC y-axis *Note: In order for the equations to work, θ MUST be measured from the positive x-axis going counterclockwise! (magnitude) 7. 66 units 10 units (y-component) (the vector) 50 o (angle*) 7 6. 43 units (x-component) x-axis

College and Engineering Physics Vectors To convert from components to magnitude/direction, we use two equations. TOC y-axis *Note: In order for the equations to work, θ MUST be measured from the positive x-axis going counterclockwise! (magnitude) Ay A (y-component) (the vector) θ(angle*) 8 Ax (x-component) x-axis

College and Engineering Physics Vectors Here is an example. TOC y-axis *Note: In order for the equations to work, θ MUST be measured from the positive x-axis going counterclockwise! (magnitude) 7. 66 units 10 units (y-component) (the vector) 50 o (angle*) 9 6. 43 units (x-component) x-axis

College and Engineering Physics Vectors A unit vector is any vector with a magnitude equal to one. TOC To find a unit vector in same direction as the vector, divide the vector by its magnitude. There are three special unit vectors… 1. 2. 3. 10 is a unit vector pointing to the right. is a unit vector pointing up. is a unit vector pointing forward.

College and Engineering Physics Vectors Any vector can be written using vector notation. TOC Vector notation uses the special unit vectors. As an example 11

College and Engineering Physics Vectors When adding vectors add their components. TOC 12

College and Engineering Physics Vectors Here is an example of adding vectors. TOC 13

College and Engineering Physics Vectors To add vectors when you are given magnitude/direction, convert to components first. TOC 14

College and Engineering Physics Vectors Here is an example of adding vectors when only their magnitude and direction are given TOC 15

College and Engineering Physics Vectors There are two ways to multiply vectors, but they cannot be divided TOC Dot products produce a scalar. Cross products produce a vector. 16

College and Engineering Physics Vectors When you multiply vectors to get a scalar use a dot product. TOC If you are given the vectors as components (vector notation)… 17

College and Engineering Physics Vectors Here is an example of solving a dot product. TOC 18

College and Engineering Physics Vectors When you multiply vectors to get a scalar use a dot product. TOC If you are given the vectors as magnitude/direction… * *If 19 then subtract it from 360°

College and Engineering Physics Vectors Here is another example of solving a dot product. TOC * *If 20 then subtract it from 360°

College and Engineering Physics Vectors When you multiply vectors to get a vector use a cross product. TOC If you are given the vectors as components (vector notation)… 21

College and Engineering Physics Vectors When you multiply vectors to get a vector use a cross product. TOC 22

College and Engineering Physics Vectors When you multiply vectors to get a vector use a cross product. TOC If you are given the vectors as magnitude/direction… * *If 23 then subtract it from 360° Use the right-hand rule to get the direction.

College and Engineering Physics Vectors When you multiply vectors to get a vector use a cross product. TOC * *If 24 then subtract it from 360° Use the right-hand rule to get the direction.

College and Engineering Physics Vectors Right-Hand Rule TOC 1. Point the fingers of your right hand in the direction of the vector A. 2. Curl your fingers toward the direction of the vector B. 3. The cross-product vector C is given by the direction of your thumb. 25

College and Engineering Physics Vectors Drawing Vectors TOC 1. Locate the position where the vector is being measured. 3. Label the vector with its name. Put an arrow above the name or make it boldface. 2. Draw an arrow, with a tail at the vector position, pointing in the direction of the vector and having a length proportional to its magnitude. 4. If necessary, move the vector to another position, keeping its length and direction the same. 26

College and Engineering Physics Vectors Graphical Vector Addition TOC 27

College and Engineering Physics Vectors TOC Negative Vectors y-axis x-axis 28

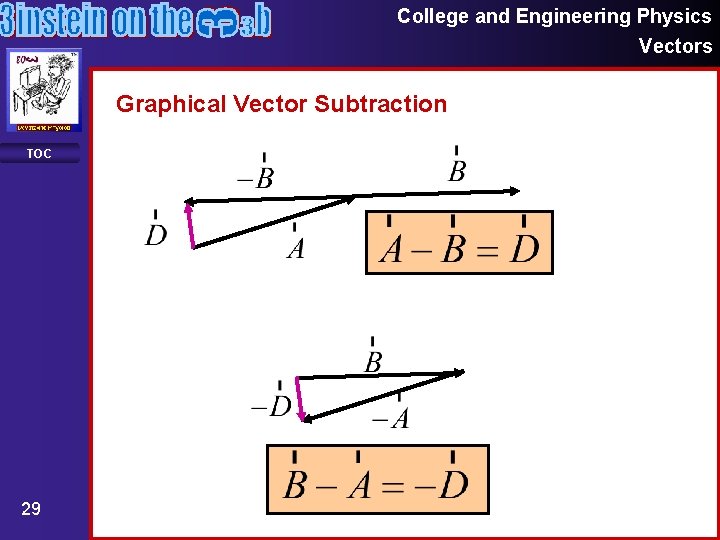
College and Engineering Physics Vectors Graphical Vector Subtraction TOC 29

College and Engineering Physics Vectors Graphical Dot Product TOC A cos f 30

College and Engineering Physics Vectors Graphical Cross Product TOC A sin f 31 The magnitude of the cross product is the area of a parallelogram that has the two vectors as its sides.

College and Engineering Physics Vectors Symmetry TOC If two vectors form a mirror image around one of the axes, then the component of the resultant along that axis is zero. y-axis x-axis 32

College and Engineering Physics Vectors TOC This is the last slide. Click the back button on your browser to return to the Ebook. 33