College Algebra Chapter 2 Functions and Graphs Section

College Algebra Chapter 2 Functions and Graphs Section 2. 6 Transformations of Graphs Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education.

Concepts 1. Recognize Basic Functions 2. Apply Vertical and Horizontal Translations (Shifts) 3. Apply Vertical and Horizontal Shrinking and Stretching 4. Apply Reflections Across the x- and y-Axes 5. Summarize Transformations of Graphs Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-2

Concept 1 Recognize Basic Functions Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-3

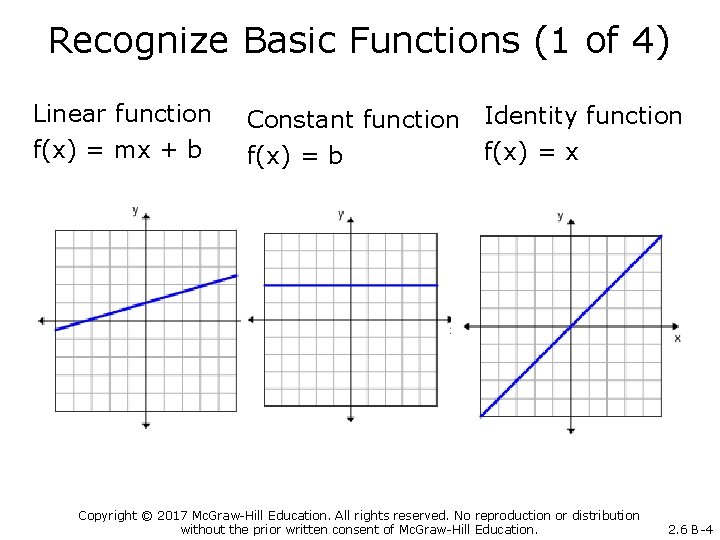
Recognize Basic Functions (1 of 4) Linear function f(x) = mx + b Constant function Identity function f(x) = x f(x) = b Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-4

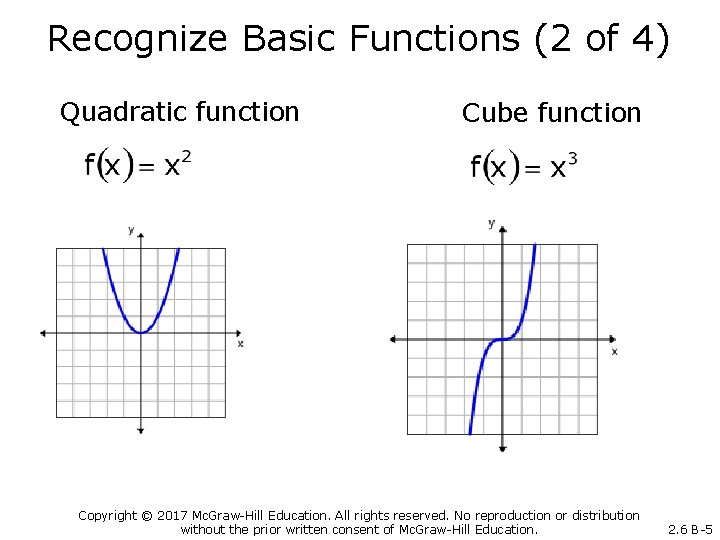
Recognize Basic Functions (2 of 4) Quadratic function Cube function Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-5

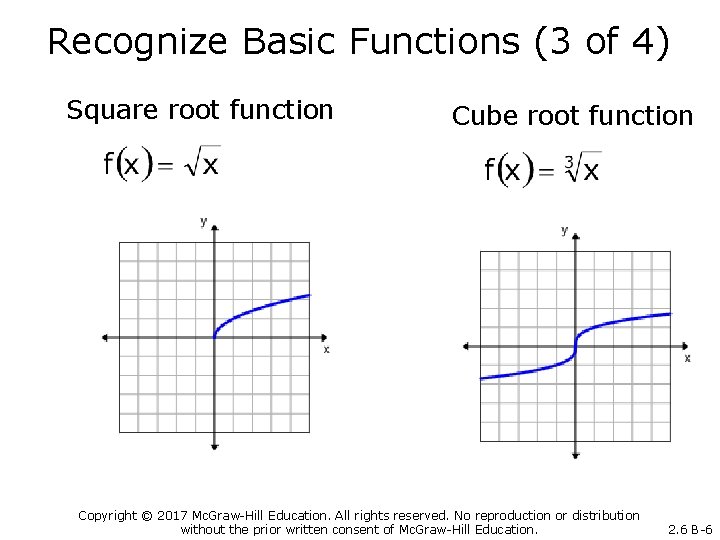
Recognize Basic Functions (3 of 4) Square root function Cube root function Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-6

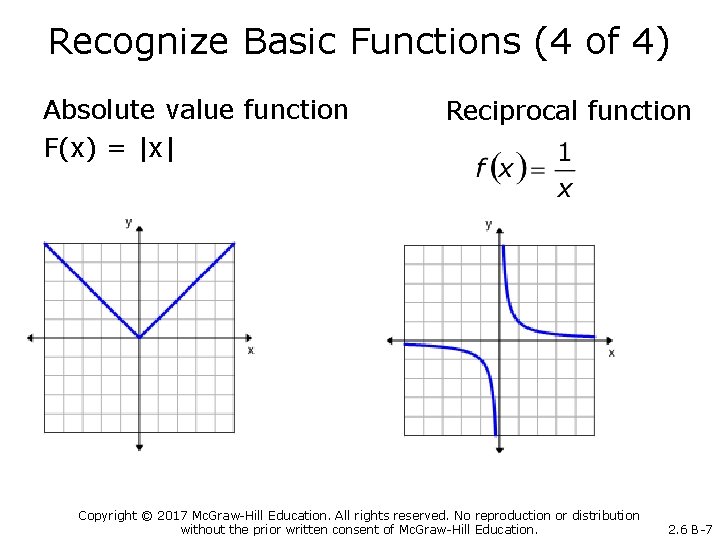
Recognize Basic Functions (4 of 4) Absolute value function F(x) = |x| Reciprocal function Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-7

Concept 2 Apply Vertical and Horizontal Translations (Shifts) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-8

Apply Vertical and Horizontal Translations (Shifts) (1 of 2) Consider a function defined by y = f(x). Let c and h represent positive real numbers. Vertical shift: The graph of y = f(x) + c is the graph of y = f(x) shifted c units upward. The graph of y = f(x) – c is the graph of y = f(x) shifted c units downward. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-9

Apply Vertical and Horizontal Translations (Shifts) (2 of 2) Horizontal shift: The graph of y = f(x – h) is the graph of y = f(x) shifted h units to the right. The graph of y = f(x + h) is the graph of y = f(x) shifted h units to the left. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-10

Example 1 (1 of 2) Graph the functions. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-11

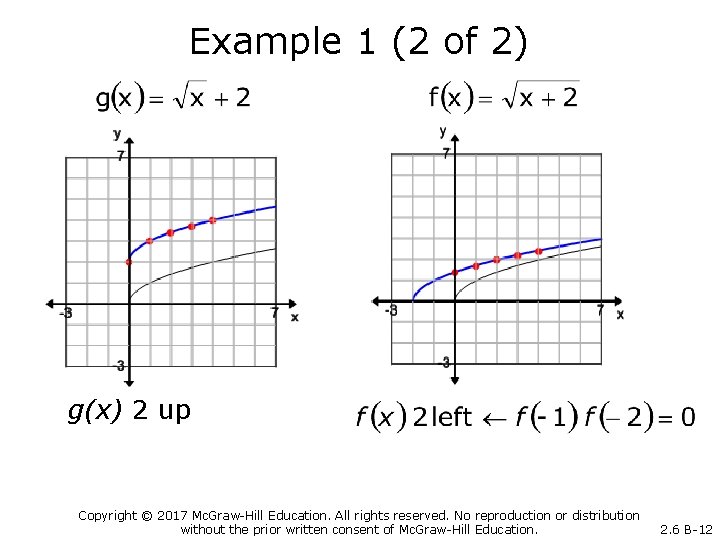
Example 1 (2 of 2) g(x) 2 up Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-12

Example 2 (1 of 2) Graph the functions. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-13

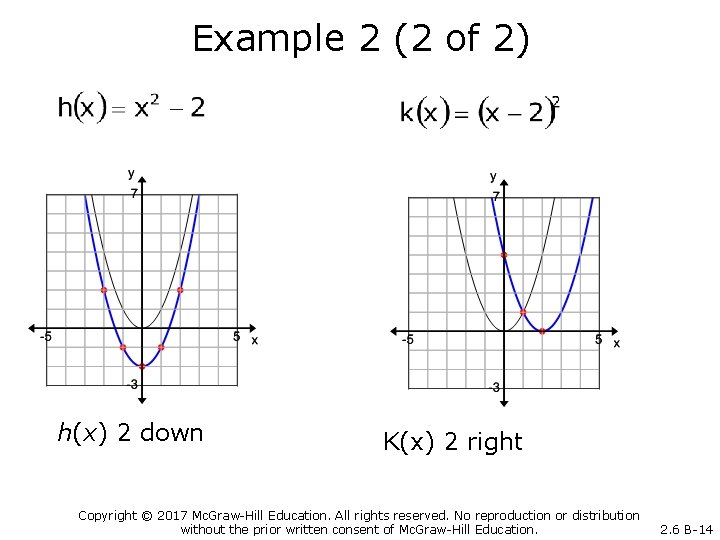
Example 2 (2 of 2) h(x) 2 down K(x) 2 right Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-14

Skill Practice 1 Use translations to graph the given function. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-15

Skill Practice 2 Graph the function defined by g(x) = |x+2|. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-16

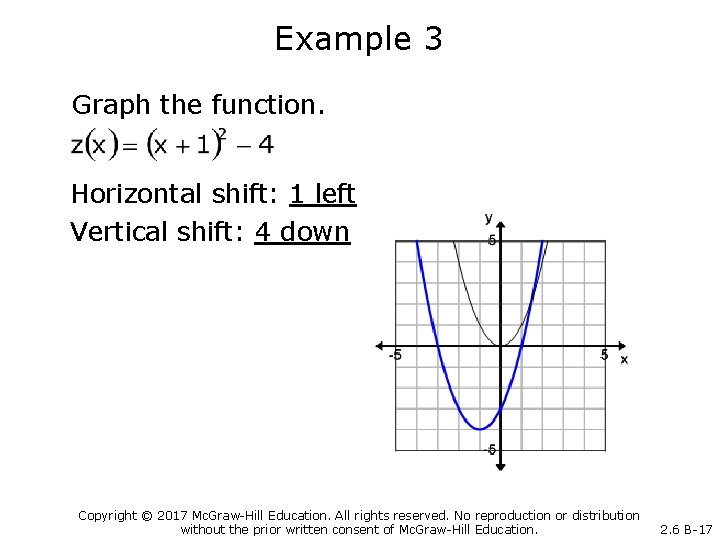
Example 3 Graph the function. Horizontal shift: 1 left Vertical shift: 4 down Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-17

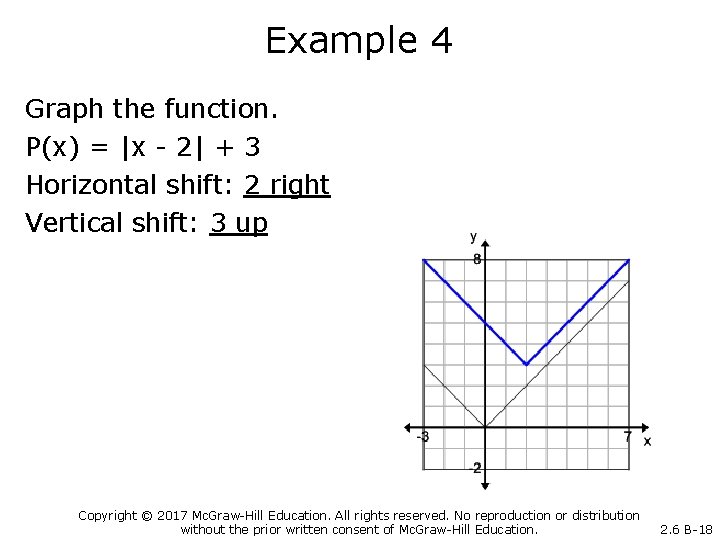
Example 4 Graph the function. P(x) = |x - 2| + 3 Horizontal shift: 2 right Vertical shift: 3 up Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-18

Skill Practice 3 Use translations to graph the function defined by Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-19

Concept 3 Apply Vertical and Horizontal Shrinking and Stretching Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-20

Apply Vertical and Horizontal Shrinking and Stretching (1 of 2) Consider a function defined by y = f(x). Let a represent a positive real number. Vertical shrink/stretch: If a>1 , then the graph of y=a||f(x) is the graph of y = f(x) stretched vertically by a factor of a. If 0<a<1 , then the graph of y=a||f(x) is the graph of y = f(x) shrunk vertically by a factor of a. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-21

Apply Vertical and Horizontal Shrinking and Stretching (2 of 2) Consider a function defined by y = f(x). Let a represent a positive real number. Horizontal shrink/stretch: If a>1 , then the graph of y=f(a||x) is the graph of y = f(x) shrunk horizontal by a factor of a. If 0<a<1 , then the graph of y=f(a||x) is the graph of y = f(x) stretched horizontal by a factor of a. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-22

Example 5 (1 of 2) Graph the functions. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-23

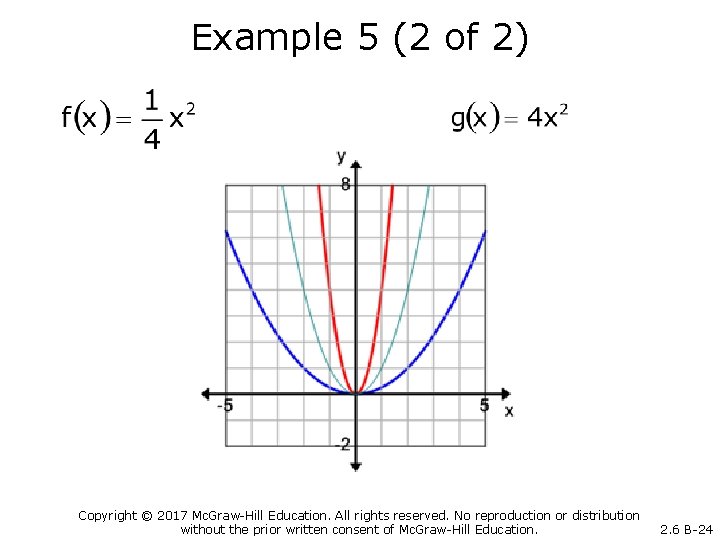
Example 5 (2 of 2) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-24

Skill Practice 4 Graph the functions. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-25

Example 6 (1 of 2) Graph the functions. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-26

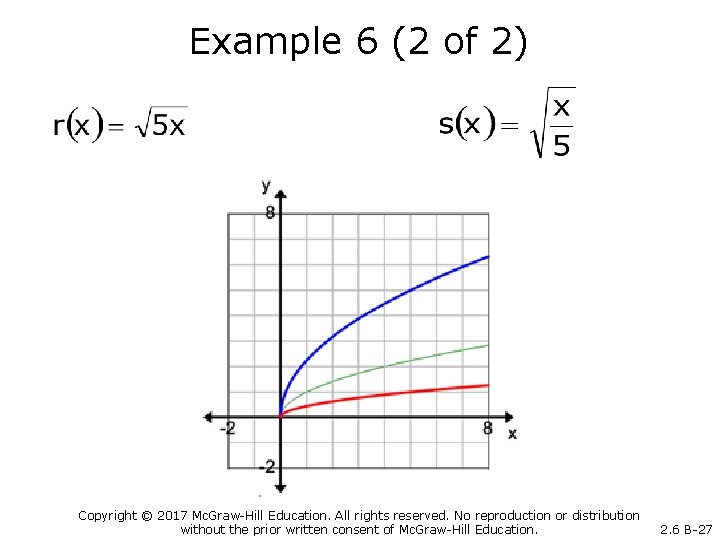
Example 6 (2 of 2) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-27

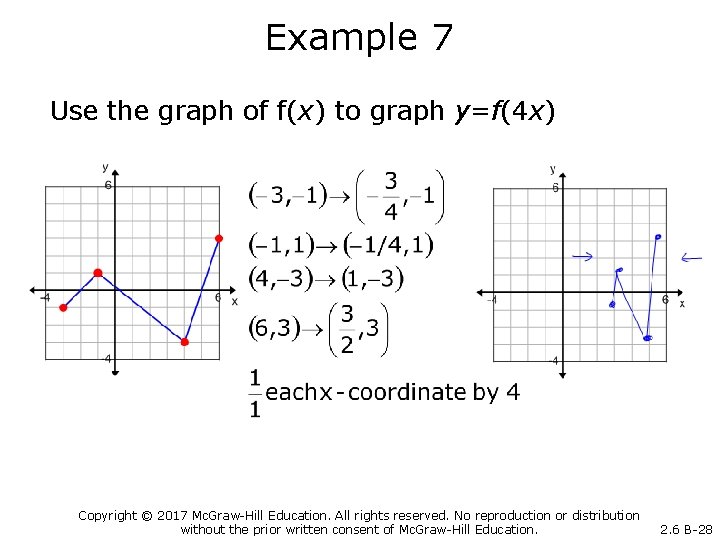
Example 7 Use the graph of f(x) to graph y=f(4 x) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-28

Skill Practice 5 The graph of y=f(x) is shown. Graph. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-29

Concept 4 Apply Reflections Across the x- and y-Axes Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-30

Apply Reflections Across the x- and y-Axes Consider a function defined by y = f(x). Reflection across the x-axis: The graph of y = – f(x) is the graph of y = f(x) reflected across the x-axis. Reflection across the y-axis: The graph of y = f(– x) is the graph of y = f(x) reflected across the y-axis. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-31

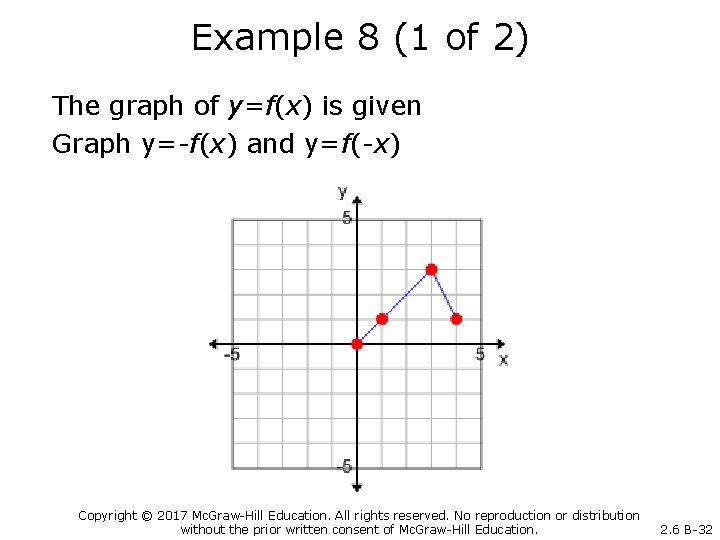
Example 8 (1 of 2) The graph of y=f(x) is given Graph y=-f(x) and y=f(-x) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-32

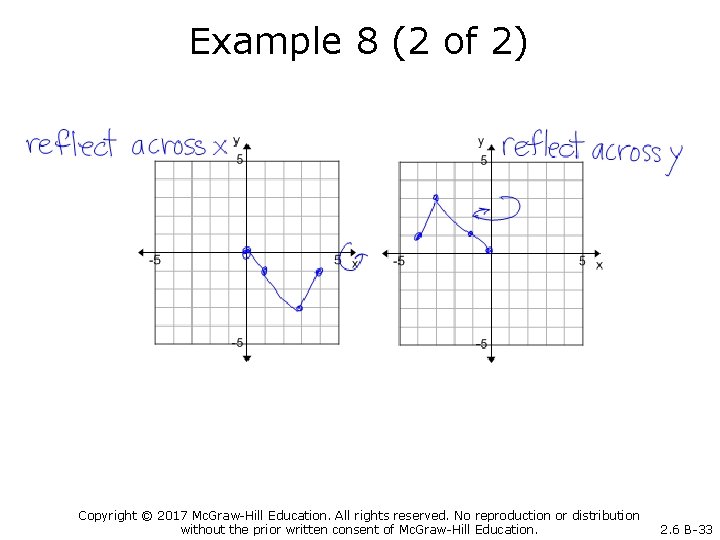
Example 8 (2 of 2) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-33

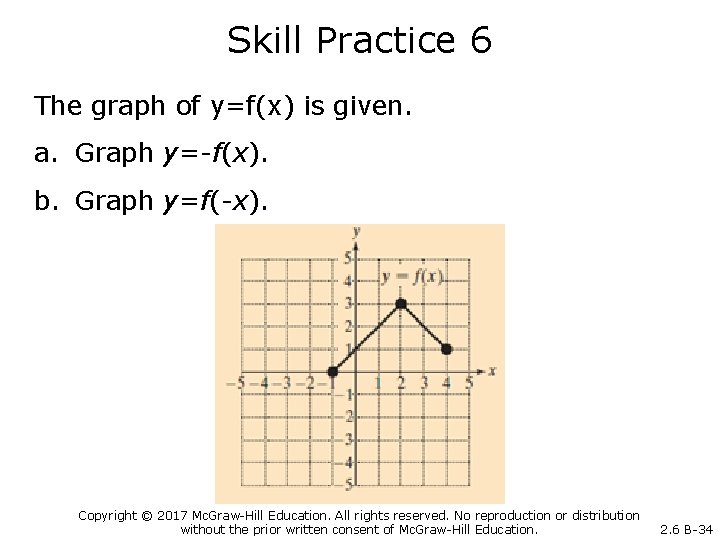
Skill Practice 6 The graph of y=f(x) is given. a. Graph y=-f(x). b. Graph y=f(-x). Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-34

Concept 5 Summarize Transformations of Graphs Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-35

Summarize of Transformations of Graphs (1 of 6) Transformations of Functions Consider a function defined by y = f(x). If c, h, and a represent positive real numbers, then the graphs of the following functions are related to y = f(x) as follows. Transformation Effect on the Graph of f Changes to Points on f Vertical translation (shift) y = f(x) + c Shift upward c units Replace (x, y) by (x, y + c) y = f(x) – c Shift downward c units Replace (x, y) by (x, y – c) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-36

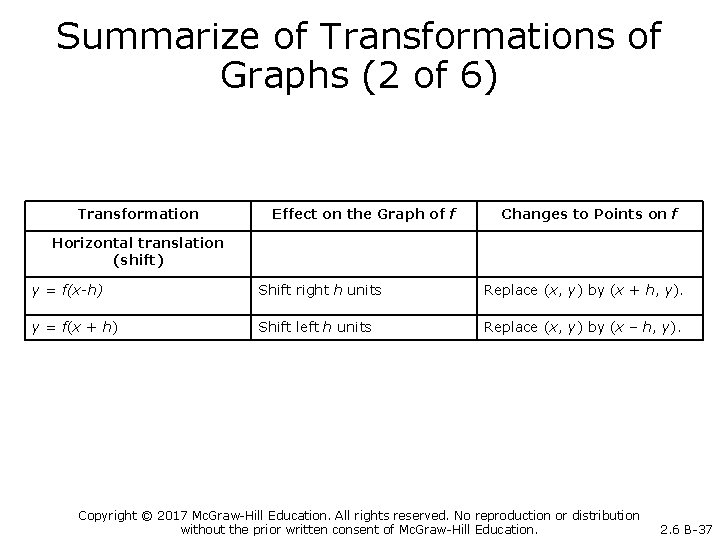
Summarize of Transformations of Graphs (2 of 6) Transformation Effect on the Graph of f Changes to Points on f Horizontal translation (shift) y = f(x-h) Shift right h units Replace (x, y) by (x + h, y). y = f(x + h) Shift left h units Replace (x, y) by (x – h, y). Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-37

Summarize of Transformations of Graphs (3 of 6) Transformation Vertical stretch/shrink y = a[f(x)] Effect on the Graph of f Changes to Points on f Vertical stretch (if a > 1) Vertical shrink (if 0 < Replace (x, y) by (x, a < 1) Graph is ay). stretched/shrunk vertically by a factor of a. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-38

Summarize of Transformations of Graphs (4 of 6) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-39

Summarize of Transformations of Graphs (5 of 6) Transformation Effect on the Graph of f Changes to Points on f Reflection y = -f(x) Reflection across the x-axis Replace (x, y) by (x, -y). y = f(-x) Reflection across the y-axis Replace (x, y) by (-x, y). Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-40

Summarize of Transformations of Graphs (6 of 6) To graph a function requiring multiple transformations, use the following order. 1. Horizontal translation (shift) 2. Horizontal and vertical stretch and shrink 3. Reflections across x- or y-axis 4. Vertical translation (shift) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-41

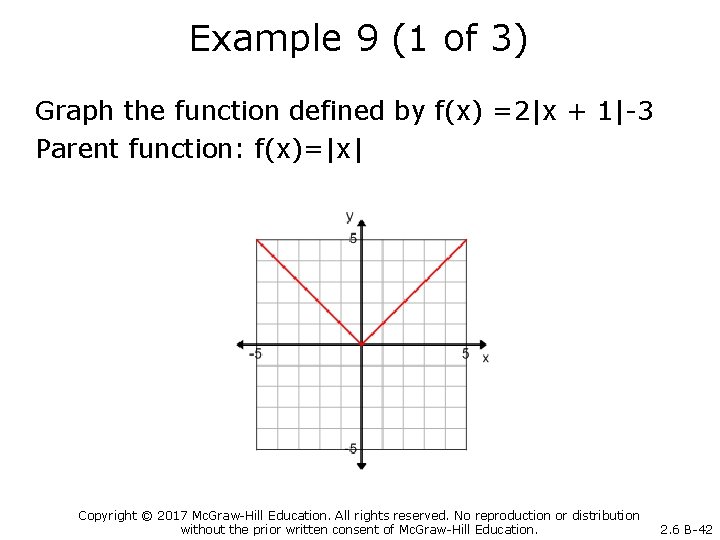
Example 9 (1 of 3) Graph the function defined by f(x) =2|x + 1|-3 Parent function: f(x)=|x| Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-42

Example 9 (2 of 3) 1. f(x) = 2|x + 1|-3 Shift the graph to the left 1 unit 2. f(x) = 2|x + 1|-3 Apply a vertical stretch (multiply the y-values by 2) 3. f(x) = 2|x + 1|-3 Shift the graph downward 3 units Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-43

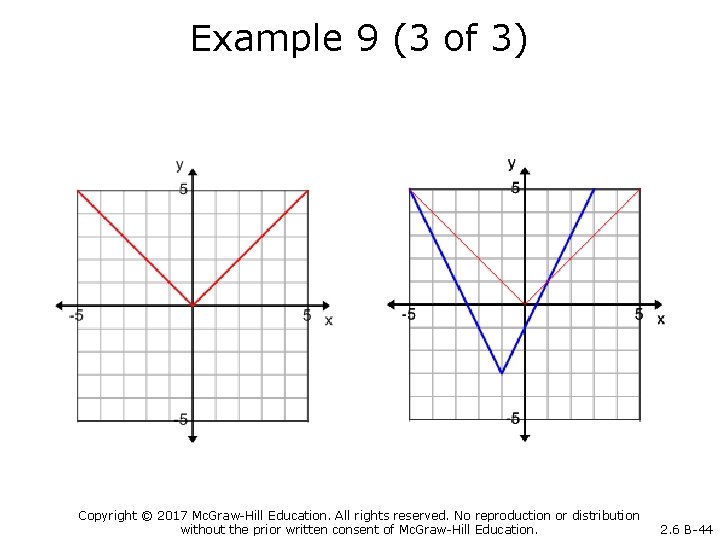
Example 9 (3 of 3) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-44

Skill Practice 7 Use transformation to graph the function defined by m(x) = -3|x - 2| -4. Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-45

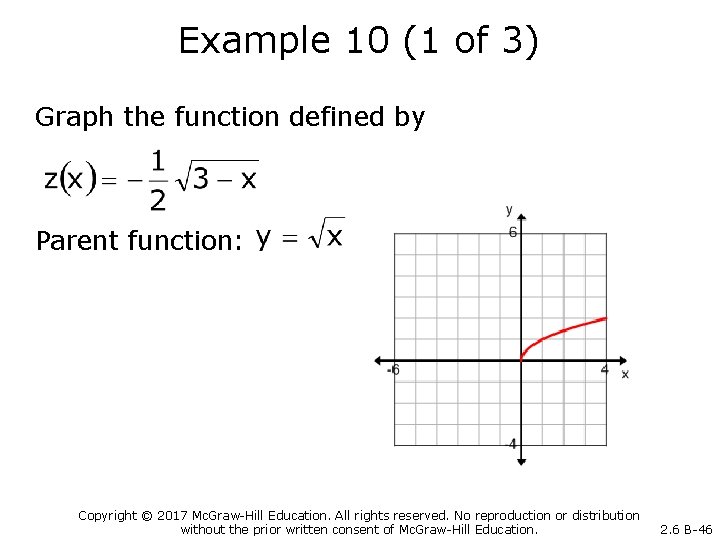
Example 10 (1 of 3) Graph the function defined by Parent function: Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-46

Example 10 (2 of 3) • Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-47

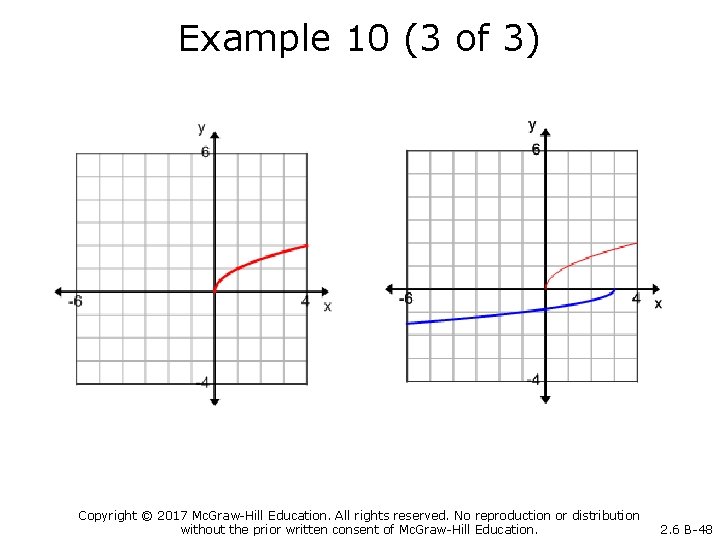
Example 10 (3 of 3) Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-48

Skill Practice 8 Use transformations to graph the function defined by Copyright © 2017 Mc. Graw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of Mc. Graw-Hill Education. 2. 6 B-49