College Algebra Chapter 1 Equations and Inequalities Section

College Algebra Chapter 1 Equations and Inequalities Section 1. 7 Linear, Compound, and Absolute Value Inequalities

Concepts 1. Solve Linear Inequalities in One Variable 2. Solve Compound Linear Inequalities 3. Solve Absolute Value Inequalities 4. Solve Applications of Inequalities

Solve Linear Inequalities in One Variable Properties of Inequality Let a, b, and c represent real numbers. These statements are also true expressed with the symbols , >, and .

Example 1: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 2: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 3: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 4: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 5: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 6: Solve the inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Concepts 1. Solve Linear Inequalities in One Variable 2. Solve Compound Linear Inequalities 3. Solve Absolute Value Inequalities 4. Solve Applications of Inequalities

Solve Compound Linear Inequalities “and” means intersection “or” means union

Example 7: Solve the compound inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 8: Solve the compound inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 9: Solve the compound inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Example 10: Solve the compound inequality. Graph the solution set, and write the solution in set-builder notation and interval notation.

Solve Compound Linear Inequalities Three-part compound inequality (x is between two values): the goal is to isolate x in the middle region

Example 11:

Example 12:

Example 13:

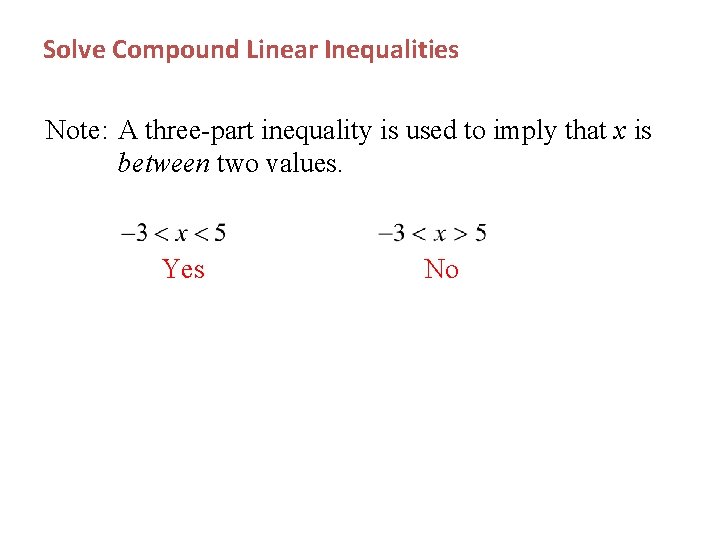
Solve Compound Linear Inequalities Note: A three-part inequality is used to imply that x is between two values. Yes No

Concepts 1. Solve Linear Inequalities in One Variable 2. Solve Compound Linear Inequalities 3. Solve Absolute Value Inequalities 4. Solve Applications of Inequalities

Solve Absolute Value Inequalities Example:

Example 14: Solve

Example 15: Solve

Solve Absolute Value Inequalities Example:

Example 16: Solve

Example 17: Solve

Example 18: Solve

Example 19: Solve

Concepts 1. Solve Linear Inequalities in One Variable 2. Solve Compound Linear Inequalities 3. Solve Absolute Value Inequalities 4. Solve Applications of Inequalities

Example 20: The p. H of the water in a public swimming pool should be maintained at a safe swimming value of 7. 4. Slight variations in the tested value of the p. H levels are acceptable but should differ from the ideal p. H level by no more than 0. 2. a. If x represents the exact p. H value tested, write an absolute value inequality that represents a safe interval for x.

Example 20 continued: b. Solve the inequality and interpret the answer.

Example 21: One cell phone service charges a flat rate of $35 a month plus 1¢ per text. Another company offers a flat monthly fee of $50 with unlimited texting. How many texts would you need to send for the first company to charge you more per month than the second company?

Example 21 continued: