Collective flow in ultrarelativistic heavyion collisions Subrata Pal

Collective flow in ultra-relativistic heavyion collisions Subrata Pal Tata Institute of Fundamental Research, Mumbai, India

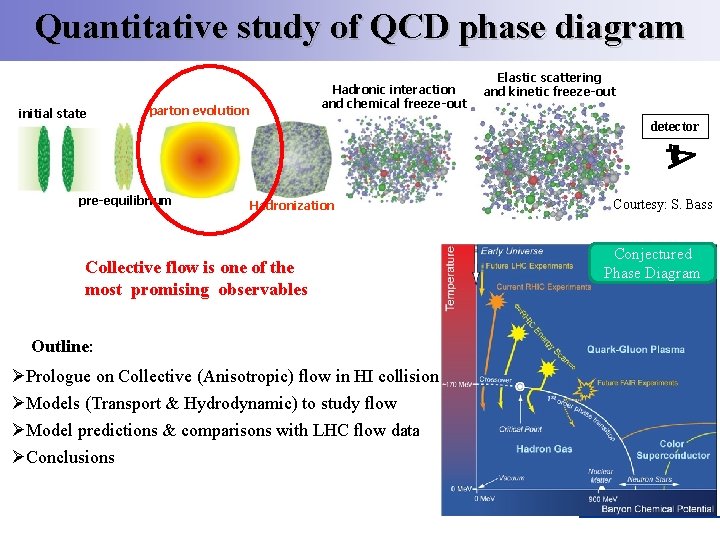
Quantitative study of QCD phase diagram initial state Hadronic interaction and chemical freeze-out parton evolution pre-equilibrium Elastic scattering and kinetic freeze-out detector Hadronization Collective flow is one of the most promising observables Outline: ØPrologue on Collective (Anisotropic) flow in HI collision ØModels (Transport & Hydrodynamic) to study flow ØModel predictions & comparisons with LHC flow data ØConclusions Courtesy: S. Bass Conjectured Phase Diagram

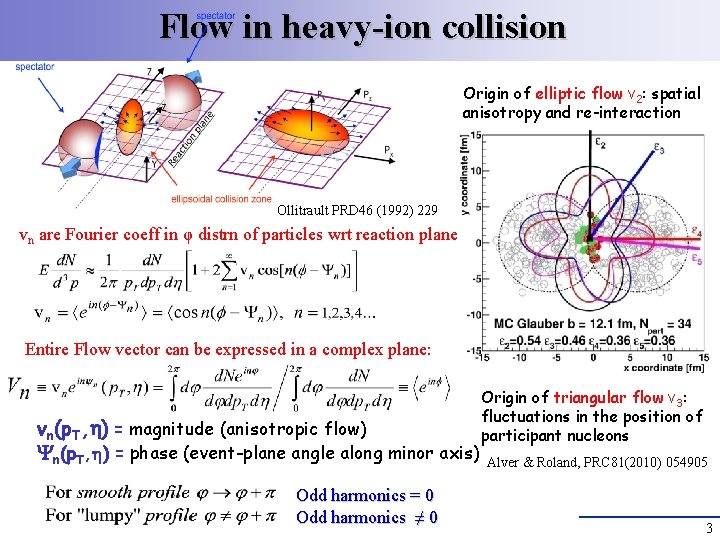
Flow in heavy-ion collision Origin of elliptic flow v 2: spatial anisotropy and re-interaction Ollitrault PRD 46 (1992) 229 vn are Fourier coeff in φ distrn of particles wrt reaction plane Entire Flow vector can be expressed in a complex plane: vn(p. T, ) = magnitude (anisotropic flow) n(p. T, ) = phase (event-plane angle along minor axis) Odd harmonics = 0 Odd harmonics ≠ 0 Origin of triangular flow v 3: fluctuations in the position of participant nucleons Alver & Roland, PRC 81(2010) 054905 3

Initial spatial anisotopy collective flow Harmonic flow vector relates to various moments of initial spatial anisotropy (eccentricities) of nucleons/partons ε 2 ε 3 … over (r, ) of participants (nucleons/partons) n = magnitude (eccenticities) n = phase (participant-plane angle) ε 4 In HI collision, Npart is finite and (r, ) fluctuate randomly Eby. E distribution: p( n, m, …. , n, m, …) Collective/Hydro expansion ( , Eo. S, /s, …) Ideal Flow observable: Joint probability distribution of all vn and n Finite multiplicity only allows projections of full p(vn, . . , n, . . ) on finite number of variables 4

Flow observables All info on Vn can be obtained from multi-particle correlations (cumulants) 2 -particle correlation: nonflow (short range: resonance decay, BE correlation, etc) Supress nonflow by placing -gaps between pairs Moments for m-particle azimuthal correlation: Azimuthal asymmetry implies n 1+…+ nm = 0 Observables of flow and Eby. E flow fluctuations: v. Flow magnitude involving vn: Cumulants & moments of p(vn), p(vn, vm) p(vn) p(vn, vm) v. Flow phases (event plane angles) involving n v. Correlation involving mixed flow harmonics Large number of flow observables promise to constrain initial matter (QGP) properties 5

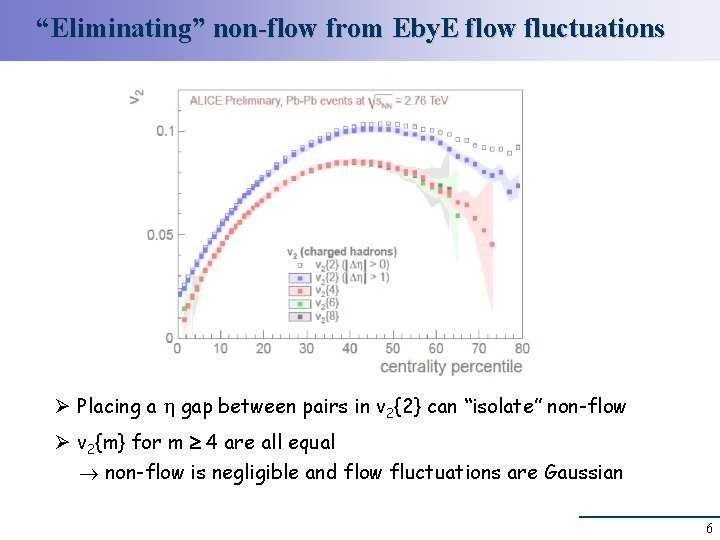
“Eliminating” non-flow from Eby. E flow fluctuations Ø Placing a gap between pairs in v 2{2} can “isolate” non-flow Ø v 2{m} for m 4 are all equal non-flow is negligible and flow fluctuations are Gaussian 6

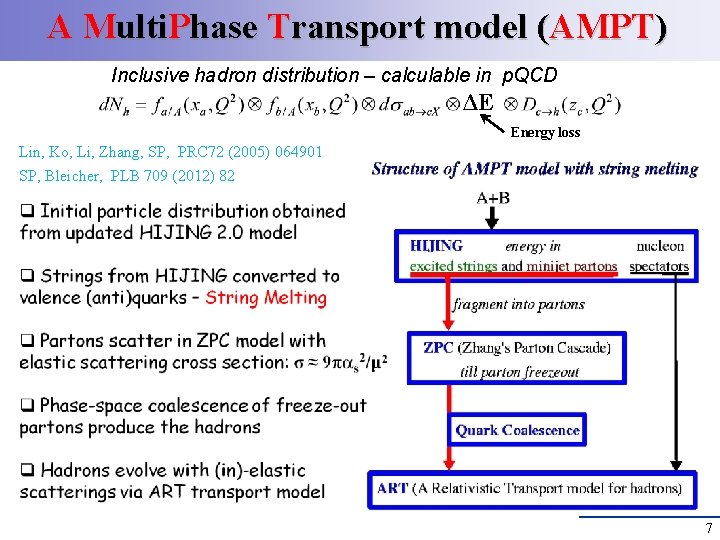
A Multi. Phase Transport model (AMPT) Inclusive hadron distribution – calculable in p. QCD ΔE Energy loss Lin, Ko, Li, Zhang, SP, PRC 72 (2005) 064901 SP, Bleicher, PLB 709 (2012) 82 7

Ideal and Dissipative Hydrodynamics Israel, Stewart, Ann. Phys. 118 (1979) 341. Muronga, PRC 69 (2004) 034903. Romatschke, Int. J. Mod. Phys. E 19 (2010) 1. Huovinen, Petreczky, NPA 837 (2010) 26 s 95 p-PCE Eo. S matching lattice data to hadron reson gas at TPCE 165 Me. V Hadron spectra at freeze-out temp. Tdec 120 Me. V obtained by Cooper-Frye formula 8

Non-equilibrium distribution function Grad, Comm. Pure App. Math 2 (1949) 2 Chapman-Enskog like derivation Bhalerao, Jaiswal, SP, Sreekanth, PRC 89 (2014) 055903 9

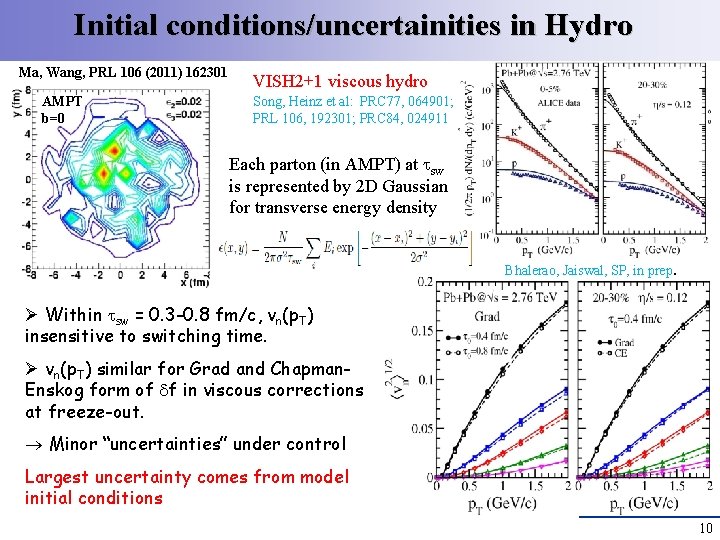
Initial conditions/uncertainities in Hydro Ma, Wang, PRL 106 (2011) 162301 AMPT b=0 VISH 2+1 viscous hydro Song, Heinz et al: PRC 77, 064901; PRL 106, 192301; PRC 84, 024911 Each parton (in AMPT) at sw is represented by 2 D Gaussian for transverse energy density Bhalerao, Jaiswal, SP, in prep. Ø Within sw = 0. 3 -0. 8 fm/c, vn(p. T) insensitive to switching time. Ø vn(p. T) similar for Grad and Chapman. Enskog form of f in viscous corrections at freeze-out. Minor “uncertainties” under control Largest uncertainty comes from model initial conditions 10

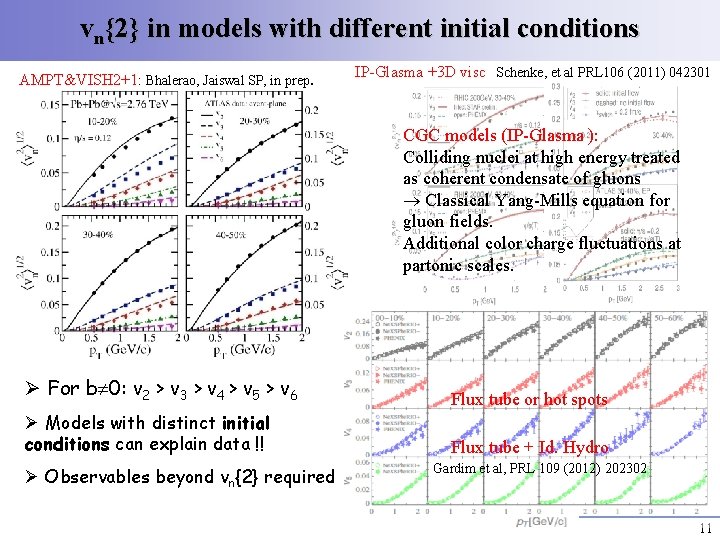
vn{2} in models with different initial conditions AMPT&VISH 2+1: Bhalerao, Jaiswal SP, in prep. IP-Glasma +3 D visc Schenke, et al PRL 106 (2011) 042301 CGC models (IP-Glasma ): Colliding nuclei at high energy treated as coherent condensate of gluons Classical Yang-Mills equation for gluon fields. Additional color charge fluctuations at partonic scales. Ø For b 0: v 2 > v 3 > v 4 > v 5 > v 6 Ø Models with distinct initial conditions can explain data !! Ø Observables beyond vn{2} required Flux tube or hot spots Flux tube + Id. Hydro Gardim et al, PRL 109 (2012) 202302 11

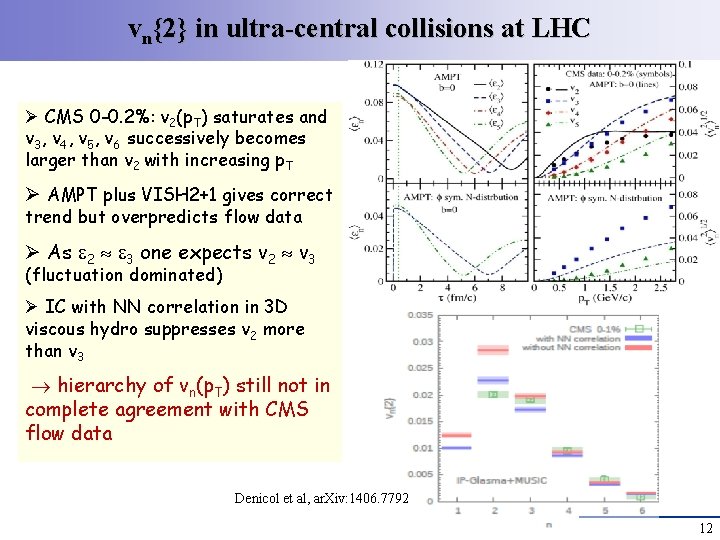
vn{2} in ultra-central collisions at LHC Ø CMS 0 -0. 2%: v 2(p. T) saturates and v 3, v 4, v 5, v 6 successively becomes larger than v 2 with increasing p. T Ø AMPT plus VISH 2+1 gives correct trend but overpredicts flow data Ø As 2 3 one expects v 2 v 3 (fluctuation dominated) Ø IC with NN correlation in 3 D viscous hydro suppresses v 2 more than v 3 hierarchy of vn(p. T) still not in complete agreement with CMS flow data Denicol et al, ar. Xiv: 1406. 7792 12

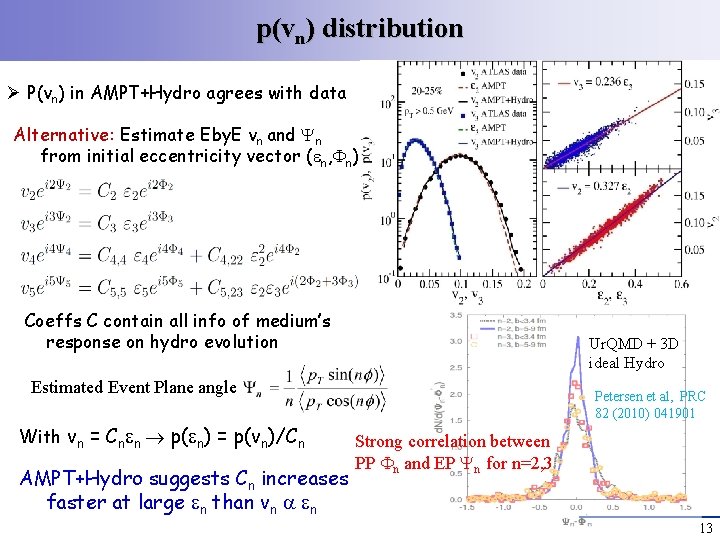
p(vn) distribution Ø P(vn) in AMPT+Hydro agrees with data Alternative: Estimate Eby. E vn and n from initial eccentricity vector ( n, n) Coeffs C contain all info of medium’s response on hydro evolution Ur. QMD + 3 D ideal Hydro Estimated Event Plane angle With vn = Cn n p( n) = p(vn)/Cn AMPT+Hydro suggests Cn increases faster at large n than vn n Petersen et al, PRC 82 (2010) 041901 Strong correlation between PP n and EP n for n=2, 3 13

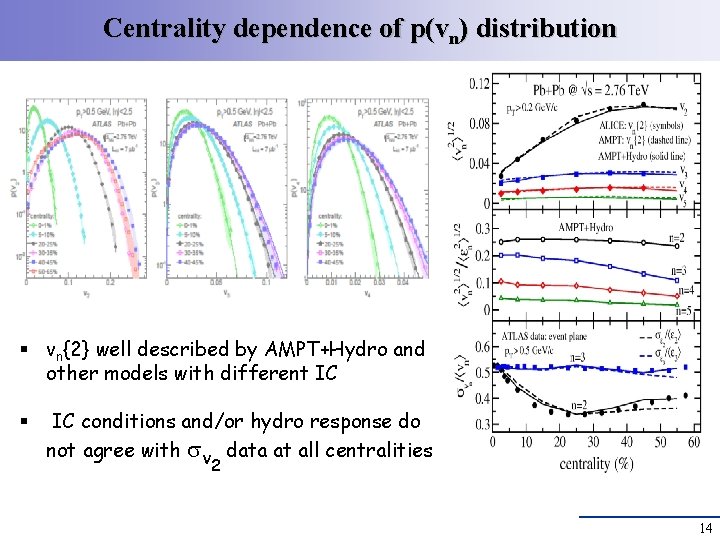
Centrality dependence of p(vn) distribution § vn{2} well described by AMPT+Hydro and other models with different IC § IC conditions and/or hydro response do not agree with v data at all centralities 2 14

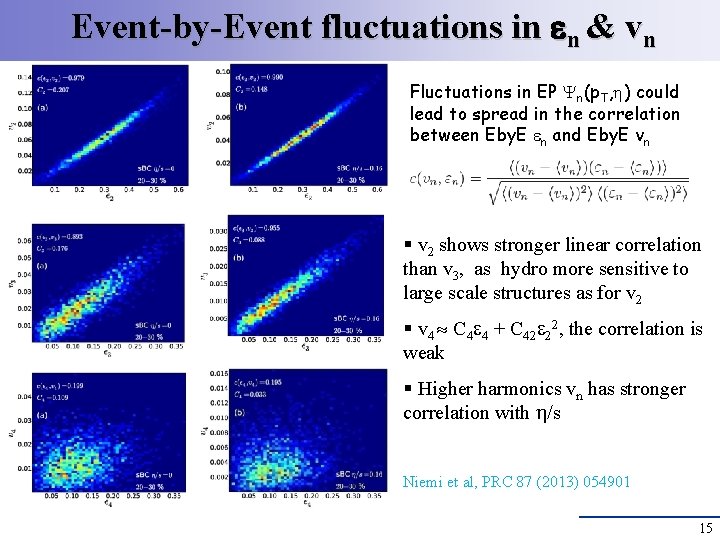
Event-by-Event fluctuations in n & vn Fluctuations in EP n(p. T, ) could lead to spread in the correlation between Eby. E n and Eby. E vn § v 2 shows stronger linear correlation than v 3, as hydro more sensitive to large scale structures as for v 2 § v 4 C 4 4 + C 42 22, the correlation is weak § Higher harmonics vn has stronger correlation with /s Niemi et al, PRC 87 (2013) 054901 15

Event plane correlations p( n, m, . . . ) EP correlators involve 3 -particles higher order correlations vn measured with single EP: Res n Correlations from multi-particles: {EP} {SP} Res( 1) Res(2 2) … Res(kn n) k 1+2 k 2+…+nkn=0 Experimental analysis: (i) each EP in different -window; (ii) windows pairwise separated by gaps decrease statistics 2 -subevent method for EP correlators Bhalerao, Ollitrault, SP, PRC 88 (2013) 024909 Consider 2 subevents (A, B) separated by a -gap. Construct flow vector for each subevent: EP method: Scalar product method: Resolution dependent Well-defined flow observable 16

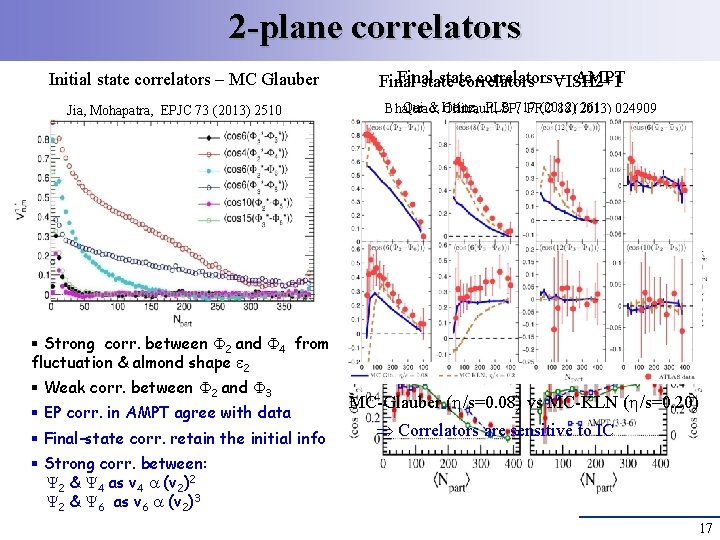
2 -plane correlators Initial state correlators – MC Glauber Jia, Mohapatra, EPJC 73 (2013) 2510 Final state correlators – AMPT Final state correlators – VISH 2+1 Qui & Heinz, PLB (2012) 261 024909 Bhalerao, Ollitrault, SP, 717 PRC 88 (2013) EP EP § Strong corr. between 2 and 4 from fluctuation & almond shape 2 § Weak corr. between 2 and 3 § EP corr. in AMPT agree with data § Final-state corr. retain the initial info MC-Glauber ( /s=0. 08) vs MC-KLN ( /s=0. 20) Correlators are sensitive to IC § Strong corr. between: 2 & 4 as v 4 (v 2)2 2 & 6 as v 6 (v 2)3 17

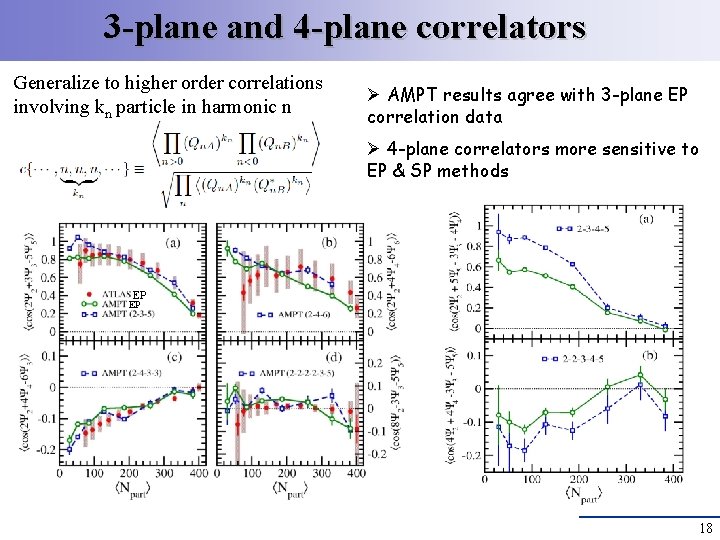
3 -plane and 4 -plane correlators Generalize to higher order correlations involving kn particle in harmonic n Ø AMPT results agree with 3 -plane EP correlation data Ø 4 -plane correlators more sensitive to EP & SP methods EP EP 18

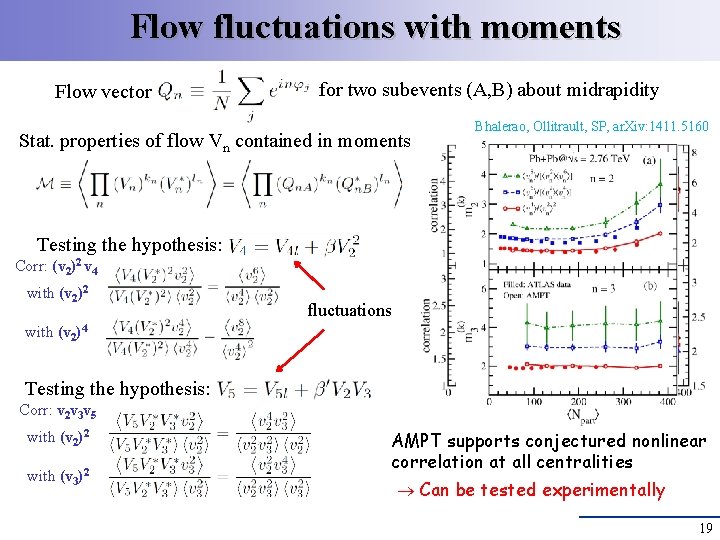
Flow fluctuations with moments Flow vector for two subevents (A, B) about midrapidity Stat. properties of flow Vn contained in moments Bhalerao, Ollitrault, SP, ar. Xiv: 1411. 5160 Testing the hypothesis: Corr: (v 2)2 v 4 with (v 2)2 fluctuations with (v 2)4 Testing the hypothesis: Corr: v 2 v 3 v 5 with (v 2)2 with (v 3)2 AMPT supports conjectured nonlinear correlation at all centralities Can be tested experimentally 19

New method to study e-by-e flow fluctuations Single particle distribution: Pair distrbn as Eby. E single distrbn: Fourier coeff. Vn(p) Vn(p. T, ) Statistics of Vn(p) embedded in Fourier Coeff: Construct bins in p (p. T, ). Estimate Vn(p) in a event with: Covariance matrix Eigenvalues 0 Pair correln: Principal Component Analysis (PCA): Diagonalize PC: self-corr. >0 (flow) <0 (non-flow) with eigenvalues: =1 (no flow fluctuations) and >1 give statistics and momentum dependence of flow fluctuations Bhalerao, Ollitrault, SP, Teaney: ar. Xiv: 1410. 7739 20

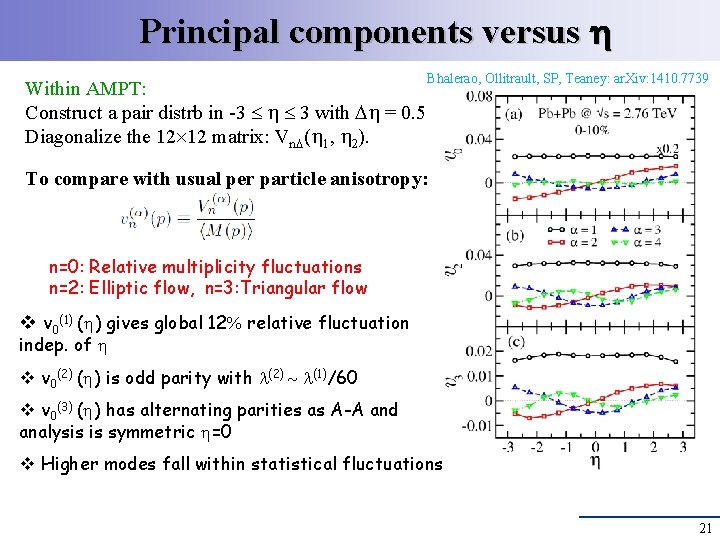
Principal components versus Within AMPT: Construct a pair distrb in -3 3 with = 0. 5 Diagonalize the 12 12 matrix: Vn ( 1, 2). Bhalerao, Ollitrault, SP, Teaney: ar. Xiv: 1410. 7739 To compare with usual per particle anisotropy: n=0: Relative multiplicity fluctuations n=2: Elliptic flow, n=3: Triangular flow v v 0(1) ( ) gives global 12 relative fluctuation indep. of v v 0(2) ( ) is odd parity with (2) (1)/60 v v 0(3) ( ) has alternating parities as A-A and analysis is symmetric =0 v Higher modes fall within statistical fluctuations 21

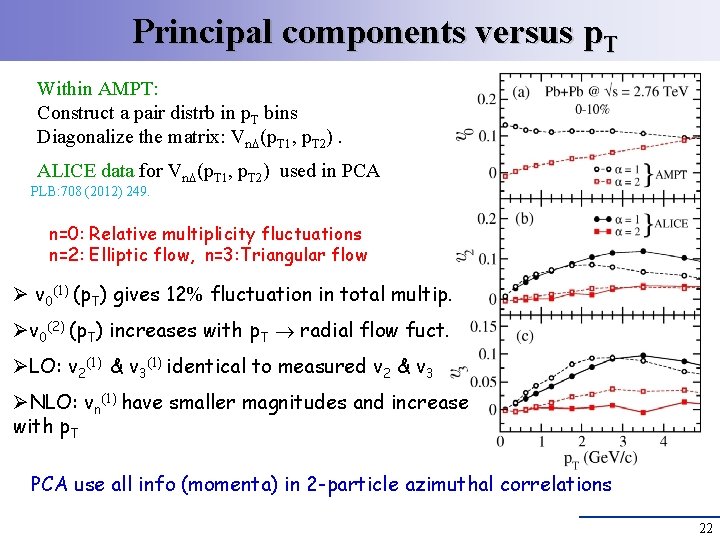
Principal components versus p. T Within AMPT: Construct a pair distrb in p. T bins Diagonalize the matrix: Vn (p. T 1, p. T 2). ALICE data for Vn (p. T 1, p. T 2) used in PCA PLB: 708 (2012) 249. n=0: Relative multiplicity fluctuations n=2: Elliptic flow, n=3: Triangular flow Ø v 0(1) (p. T) gives 12 fluctuation in total multip. Øv 0(2) (p. T) increases with p. T radial flow fuct. ØLO: v 2(1) & v 3(1) identical to measured v 2 & v 3 ØNLO: vn(1) have smaller magnitudes and increase with p. T PCA use all info (momenta) in 2 -particle azimuthal correlations 22

Summary & Conclusions v Ultimate goal: First principal calculation of non-equilibrium QCD for initial stages of HIC not yet possible v Pragmatic approach: Use “state-of-art” models to constrain the required initial state structures from experimental data v Observable: Anisotropic flow and flow fluctuations provide large number independent info. v Open issues: vn{2} hierarchy in ultra-central collisions; p(vn) distribution, multiparticle correlation analysis further constrain the initial condition 23

24

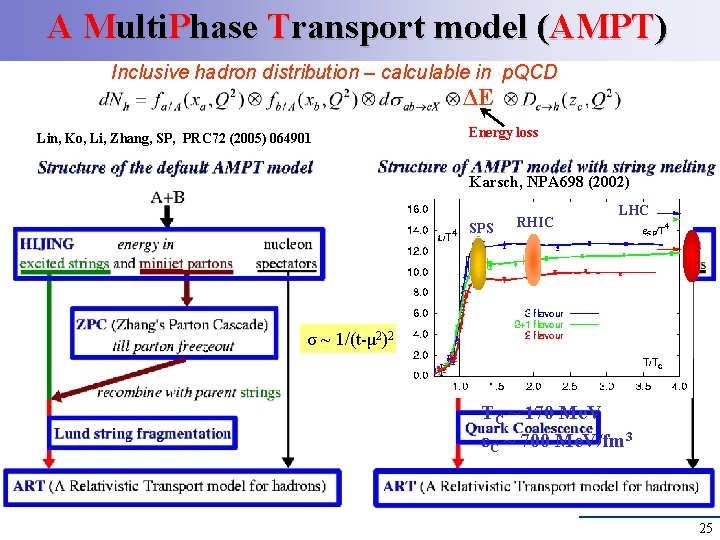
A Multi. Phase Transport model (AMPT) Inclusive hadron distribution – calculable in p. QCD ΔE Lin, Ko, Li, Zhang, SP, PRC 72 (2005) 064901 Energy loss Karsch, NPA 698 (2002) SPS RHIC LHC σ ~ 1/(t-μ 2)2 TC ~ 170 Me. V εC ~ 700 Me. V/fm 3 25

Hard jets & its energy loss in AMPT Momentum distribution of hard partons from LO p. QCD in p+p collision Gaussian NLO GRV 94 Total energy loss by a jet of energy E via gluon radiation L = 3 fm, αS = 0. 48 Parton density # of gluons emitted from energy loss ΔE is related to entropy increase ΔS T= ε(r , τ)/parton 3ρ(r, τ ) From cascade Radiated gluons scatter in medium with σ ~ 1/(t-μ 2)2 Parton hadron duality: Ng → Nπ 26

AMPT with updated HIJING 2. 0 • GRV parametrization of parton distribution function Deng, Wang, Xu, PLB 701 (2011) 133 PDF in nucleus: Impact parameter dependent shadowing sq = 0. 1 (fixed) from deep-inelastic- scattering data off nuclear targets. sg fitted to centrality dependence of measured d. Nch/dy in A+A collision.

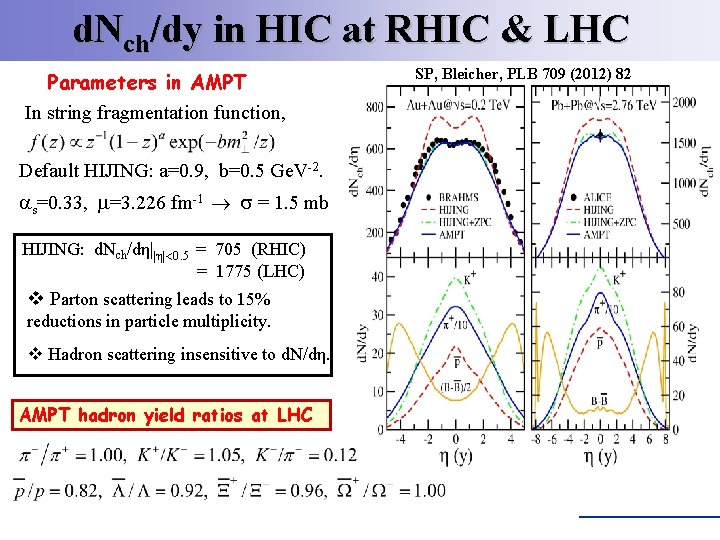
d. Nch/dy in HIC at RHIC & LHC Parameters in AMPT In string fragmentation function, Default HIJING: a=0. 9, b=0. 5 Ge. V-2. s=0. 33, =3. 226 fm-1 = 1. 5 mb HIJING: d. Nch/dη||η| 0. 5 = 705 (RHIC) = 1775 (LHC) v Parton scattering leads to 15% reductions in particle multiplicity. v Hadron scattering insensitive to d. N/dη. AMPT hadron yield ratios at LHC SP, Bleicher, PLB 709 (2012) 82

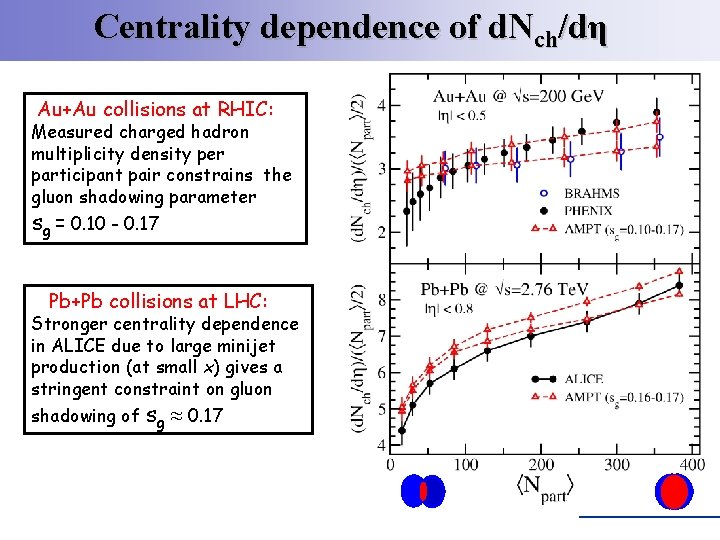
Centrality dependence of d. Nch/dη Au+Au collisions at RHIC: Measured charged hadron multiplicity density per participant pair constrains the gluon shadowing parameter sg = 0. 10 - 0. 17 Pb+Pb collisions at LHC: Stronger centrality dependence in ALICE due to large minijet production (at small x) gives a stringent constraint on gluon shadowing of sg ≈ 0. 17 [5]