Coleridge Maths Problem Solving and the New Curriculum

Coleridge Maths Problem Solving and the New Curriculum Conceptual Understanding Pupils become fluent in the fundamentals of mathematics, so that they develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately. Mathematical Reasoning Pupils reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language. Problem Solving Pupils can solve problems by applying their mathematics to a variety of routine and nonroutine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

Coleridge Maths Problem Solving and the New Curriculum ‘Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content’ (NC 2014)

Coleridge Maths Problem Solving • • Trial and Improvement Working Systematically Pattern Spotting Working Backwards Reasoning Visualising Conjecturing, Generalising and Proving

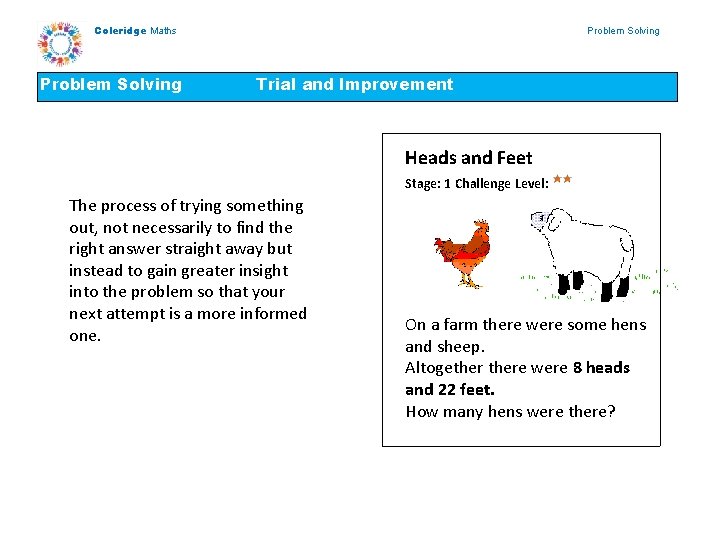
Coleridge Maths Problem Solving Trial and Improvement Heads and Feet Stage: 1 Challenge Level: The process of trying something out, not necessarily to find the right answer straight away but instead to gain greater insight into the problem so that your next attempt is a more informed one. On a farm there were some hens and sheep. Altogethere were 8 heads and 22 feet. How many hens were there?

Coleridge Maths Problem Solving Working Systematically Working in a methodical and efficient way to ensure you find all the possibilities. Three Ball Line Up Stage: 1 Challenge Level: Two children are playing with three balls, one blue, one red and one green. They toss up the balls, which run down a slope so that they land in a row of three. How many different ways could the balls land? You might like to use the interactivity below to explore the problem.

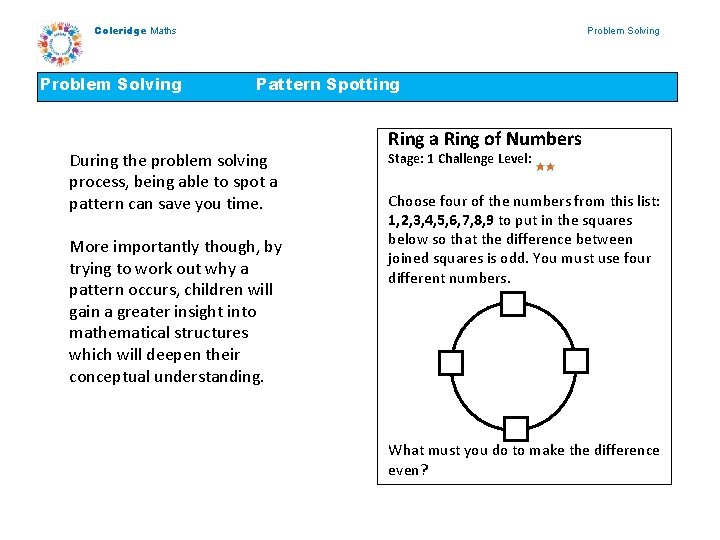
Coleridge Maths Problem Solving Pattern Spotting During the problem solving process, being able to spot a pattern can save you time. More importantly though, by trying to work out why a pattern occurs, children will gain a greater insight into mathematical structures which will deepen their conceptual understanding. Ring a Ring of Numbers Stage: 1 Challenge Level: Choose four of the numbers from this list: 1, 2, 3, 4, 5, 6, 7, 8, 9 to put in the squares below so that the difference between joined squares is odd. You must use four different numbers. What must you do to make the difference even?

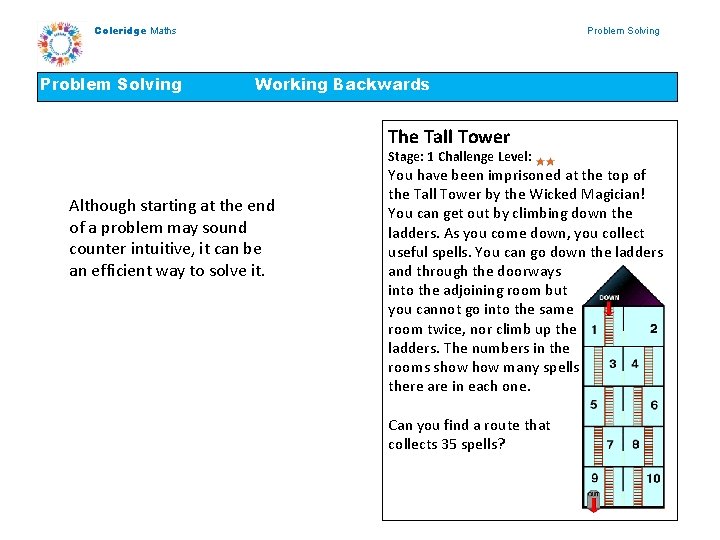
Coleridge Maths Problem Solving Working Backwards The Tall Tower Stage: 1 Challenge Level: Although starting at the end of a problem may sound counter intuitive, it can be an efficient way to solve it. You have been imprisoned at the top of the Tall Tower by the Wicked Magician! You can get out by climbing down the ladders. As you come down, you collect useful spells. You can go down the ladders and through the doorways into the adjoining room but you cannot go into the same room twice, nor climb up the ladders. The numbers in the rooms show many spells there are in each one. Can you find a route that collects 35 spells?

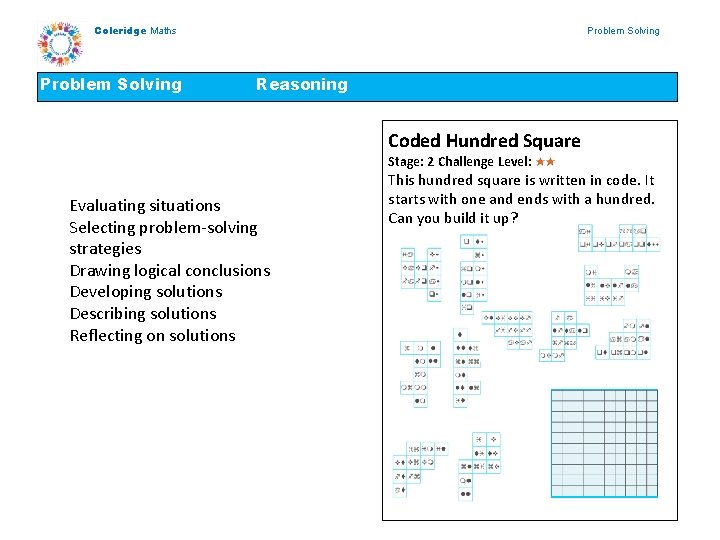
Coleridge Maths Problem Solving Reasoning Coded Hundred Square Stage: 2 Challenge Level: Evaluating situations Selecting problem-solving strategies Drawing logical conclusions Developing solutions Describing solutions Reflecting on solutions This hundred square is written in code. It starts with one and ends with a hundred. Can you build it up?

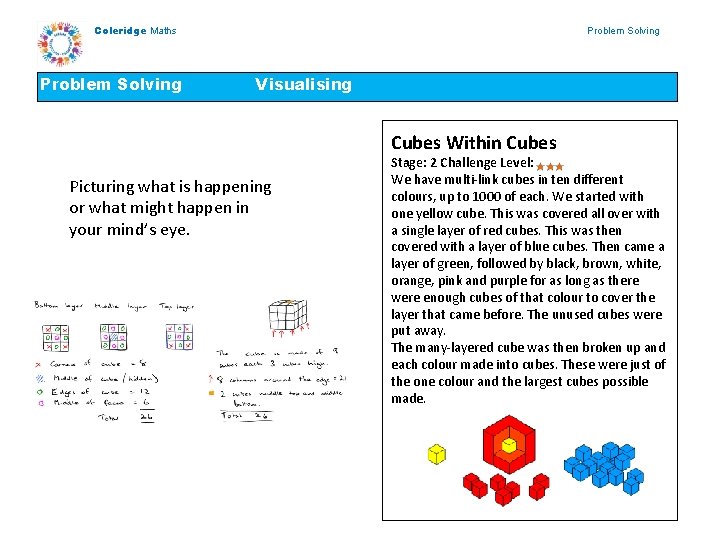
Coleridge Maths Problem Solving Visualising Cubes Within Cubes Picturing what is happening or what might happen in your mind’s eye. Stage: 2 Challenge Level: We have multi-link cubes in ten different colours, up to 1000 of each. We started with one yellow cube. This was covered all over with a single layer of red cubes. This was then covered with a layer of blue cubes. Then came a layer of green, followed by black, brown, white, orange, pink and purple for as long as there were enough cubes of that colour to cover the layer that came before. The unused cubes were put away. The many-layered cube was then broken up and each colour made into cubes. These were just of the one colour and the largest cubes possible made.

Coleridge Maths Problem Solving Conjecturing, Generalising and Proving Using similarities and differences that you find to speculate about what might happen if… An ability to make generalisations and predictions. Break it Up! Stage: 1 and 2 Challenge Level: You have a stick of 7 interlocking cubes. You cannot change the order of the cubes. You break off a bit of it leaving it in two pieces. Here are 3 of the ways in which you can do it: Shows a deeper understanding of the mathematical structure of a problem. Number of cubes Number of ways 6 cubes ? 7 cubes ? 8 cubes ? In how many different ways can it be done? Now try with a stick of 8 cubes and a stick of 6 cubes:

Coleridge Maths Problem Solving Amy's Dominoes Stage: 2 Challenge Level: Amy has a box containing ordinary domino pieces but she does not think it is a complete set. She has 24 dominoes in her box and there are 125 spots on them altogether. Which of her domino pieces are missing?

Coleridge Maths Problem Solving Use of partnered work in games to elicit constant mathematical discussion. Helps the children think through their ideas and strategies. Getting children to work out rules for the games themselves – children found this part the most challenging. Problem Solving