Colegiul Naional SILVANIA Zalu Evaluarea n programa de

























![2. Tehnica perechilor Descriere şi utilizare [I. Neacşu, A. Stoica , 1996] Tehnica perechilor 2. Tehnica perechilor Descriere şi utilizare [I. Neacşu, A. Stoica , 1996] Tehnica perechilor](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-26.jpg)







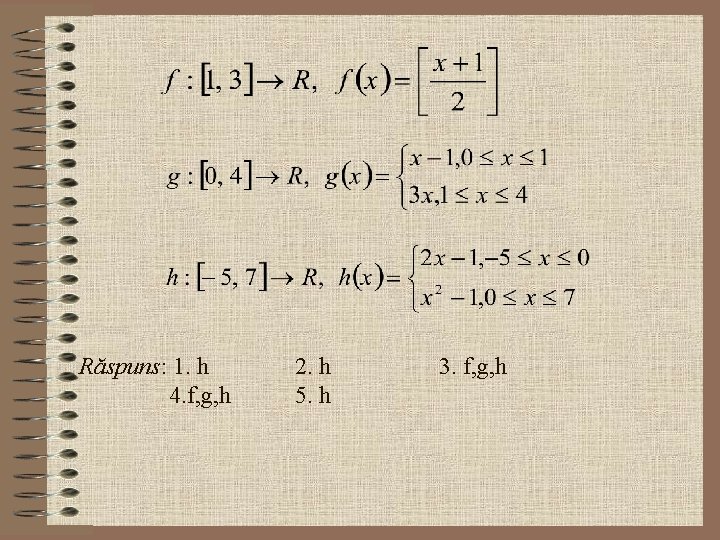
![3. Tehnica alegerii multiple Descrierea şi utilizarea [I. Neacşu, A Stoica , 1996] Itemii 3. Tehnica alegerii multiple Descrierea şi utilizarea [I. Neacşu, A Stoica , 1996] Itemii](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-35.jpg)






![Tehnici de testare – Itemi semiobiectivi Descriere [ I. Neacsu, A. Stoica, 1996 ] Tehnici de testare – Itemi semiobiectivi Descriere [ I. Neacsu, A. Stoica, 1996 ]](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-42.jpg)







![Întrebări structurate Descriere [ Stoica A. ( coordonator) 1996] O întrebare structurată este formată Întrebări structurate Descriere [ Stoica A. ( coordonator) 1996] O întrebare structurată este formată](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-50.jpg)






![Tehnici de testare – Itemi subiectivi Descriere [I. Neacşu, A. Stoica, 1996] Itemii subiectivi, Tehnici de testare – Itemi subiectivi Descriere [I. Neacşu, A. Stoica, 1996] Itemii subiectivi,](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-57.jpg)















- Slides: 72

Colegiul Naţional “SILVANIA” – Zalău Evaluarea în programa de matematică din licee prof. Florian Tuduce prof. Zay Éva

Evaluarea în programa de matematică din licee Se cunoaşte că procesul educaţional are trei componente: predare – învăţare – evaluare, primele două depinzând, în mare măsură, de modul cum este proiectată evaluarea. Evaluarea în procesul de învăţământ este o activitate de colectare, organizare şi interpretare a datelor privind efectele directe ale relaţiei profesor – elev cu scopul de a eficientiza funcţionarea întregului sistem educaţional.

Evaluarea are în primul rând un rol de feedback pentru elevi, profesori, părinţi şi factori de decizie. Deci, scopul major al evaluării este să ofere datele necesare care să permită luarea celor mai bune decizii educaţionale. Evaluarea se poate astfel raporta la unul sau mai multe dintre următoarele scopuri : a) Fundamentarea deciziilor b) Priza de cunoştinţă / Conştientizarea problemei c) Influenţarea evoluţiei sistemului evaluat

I. FORME ŞI TIPURI DE EVALUARE 1) Evaluarea iniţială -care se realizează la începutul unei secvenţe, unui capitol sau ciclu de învăţământ. 2) Evaluarea continuă -care loc pe tot parcursul desfăşurării procesului de învăţământ. Aceasta vizează nu atât comportamentele finale elevului, cât, mai ales formarea unor judecăţi asupra eficacităţii învăţării. Ea cere ca fiecare comportament realizat de elev să fie măsurat între anumite limite.

Metode şi procedee în evaluarea continuă a)Observarea şi aprecierea verbală (de tipul: „bine”, „ foarte bine”, „ai progresat” etc. ). b)Chestionarea orală Este necesar ca întrebările să depăşească cerinţa simplă de reproducere a cunoştinţelor, solicitând interpretarea şi prelucrarea lor , capacitatea de a opera cu ele, de a le aplica în practică.

Chestionarea orală poate fi: - curentă - finală Aceasta se realizează cu precădere în timpul lecţiilor şi se desfăşoară frontal sau individual. Chestionarea finală are loc în ore special destinate : la sfârşit de - capitol - semestru - an şcolar - la examene .

c) Lucrările scrise permit ca într-un timp scurt să se verifice cunoştinţele unui mare număr de elevi. d) Testele docimologice conţin seturi de itemi cu ajutorul cărora se evaluează nivelul asimilării cunoştinţelor şi al capacităţilor de a opera cu ele. Un tip special de teste docimologice îl reprezintă testele standardizate, a căror principală calitate este că pot fi administrate, cotate şi interpretate în condiţii identice (standard). Testele standardizate permit efectuarea de comparaţii între elevi sau grupuri de elevi.

e) Verificarea prin lucrări practice - oferă posibilitatea evaluării capacităţii elevilor de a aplica cunoştinţele în practică, precum şi gradul de stăpânire a priceperilor şi deprinderilor formate. f) Verificarea prin proiecte – permite o apreciere complexă şi nuanţată a învăţării şi mai ales identificarea unor elemente de performanţă individuală a elevilor.

3) Evaluarea cumulativă, sumativă sau globală - este în esenţă normativă şi se face la intervale mai mari de timp, la finele unor secvenţe temporale sau tematice (capitol, semestru, an şcolar sau ciclu de învăţământ). Aceasta oferă posibilitatea aprecierii modului în care au fost atinse obiectivele proiectate sau secvenţe ale lor acoperind un conţinut integral sau unităţi mari ale acestuia. În evaluarea sumativă, instrumentul cel mai recomandat este testul standardizat. Evaluarea de proces (a evolutiei rezultatelor şcolare) presupune o anumită metodologie, în stabilirea căreia trebuie date răspunsuri la următoarele întrebări:

· Cui foloseşte evaluarea? - elevilor - profesorilor - părinţilor - factorilor de decizie · Când evaluăm ? - de câteva ori pe an - la date fixe - continuu · Pe cine evaluăm? - toţi elevii - un anumit grup de vârstă - elevii luaţi individual · Cu ce instrumente evaluăm? - teste scrise / orale / practice - observaţia directă în clasă - teme pentru acasă - referate / proiecte

II. METODE ŞI TEHNICI DE MĂSURARE ŞI EVALUARE LA OBIECTUL MATEMATICĂ Din punctul de vedere al obiectivităţii în notare itemii se clasifică în : -itemi obiectivi -itemi semiobiectivi -itemi subiectivi ( cu răspuns deschis) Vom prezenta în continuare modul de proiectare al acestor tipuri de itemi ( însoţit de exemple):

1. Tehnica alegerii duale Tehnica se caracterizează prin solicitarea elevilor de a asocia unul sau mai multe enunţuri cu una din componentele unor cupluri de alternative duale, cum ar fi : • adevărat – fals • corect – greşit • acord – dezacord • da – nu • enunţ factual – enunţ de opinie, etc

Utilizarea tehnicii de testare cu răspuns dual a) Cunoaşterea unor noţiuni ( reguli de calcul) Exemplu: Citeşte cu atenţie afirmaţiile de mai jos. În cazul în care apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F şi înlocuieşte în spaţiul liber cuvintele subliniate care fac afirmaţia adevărată.

A F (___) 1. Fracţiile zecimale periodice reprezintă numere iraţionale. A F (___) 2. Triunghiul isoscel are toate bisectoarele congruente. A F (___) 3. Tetraedul regulat este o piramidă triunghiulară regulată. Răspuns: 1. raţionale 2. echilateral 3. A.

Avantaje şi limite ale utilizării tehnicii alegerii duale: Principalul avantaj legat de utilizarea acestei tehnici este acela al abordării, într-un interval de timp redus, a unui volum mare de rezultate ale învăţării. De obicei complexitatea acestor itemi este redusă sau medie. Una dintre cele mai întemeiate critici ce se aduc acestei tehnici este aceea că identificarea unui enunţ ca fiind incorect, neadevărat etc. nu implică în mod necesar cunoaşterea de către subiect a alternativei adevărate.

Recomandări pentru construirea itemilor, utilizând tehnica alegerii duale a) Vor fi evitate enunţurile cu caracter foarte general, atunci când se solicită aprecierea lor drept adevărate sau false Exemplu: A F 1. Rezultatul înmulţirii oricăror două numere este mai mare decât oricare dintre factori ( 8· 0, 5 =4 şi 7· 2=14 ) b) Vor fi evitate enunţuri nerelevante din punct de vedere matematic. Exemplu: A F 1. Prima carte de matematică a fost tipărită în limba română în anul 1837.

c) Vor fi evitate enunţuri a căror structură poate genera ambiguităţi sau dificultăţi de înţelegere. Exemple: A F 1. Un număr natural care nu se poate scrie sub forma 2 k este număr impar ( k Є N) Reformulare: A F 1. Un număr care se scrie sub forma 2 k + 1 este număr impar ( k Є N). d) Vor fi evitate enunţuri lungi, complexe, cu amănunte/ detalii inutile. e) Va fi evitată introducerea a două sau mai multe idei întrun enunţ ( cu excepţia situaţiilor în care se urmăreşte cunoaşterea sau înţelegerea unor relaţii cauză – efect).

Exemple de itemi Ex. 1. Disciplina / Clasa / Capitolul : Algebră / Clasa a IX-a / Funcţii Obiectivul: Elevul va fi capabil să aplice corect definiţia noţiunii de funcţie. Enunţ: Citeşte cu atenţie propoziţiile de mai jos. În cazul în care apreciezi că afirmaţia defineşte o funcţie , încercuieşte litera A. Dacă apreciezi că afirmaţia este falsă, încercuieşte litera F şi scrie în spaţiul liber subliniat o variantă corectă a domeniului de definiţie.

A F __1) Fie funcţia f: R → R , f (x) = A F __ 2) Fie funcţia f: R → R , f (x) = 2 x – 1 A F __ 3) Fie funcţia f : [ 0; 5 ] → [ 0; 2 ] , f (x) = x – 1 A F __ 4) Fie funcţia f: R → R , f (x) = A F __5) Fie funcţia f : [ 0 , ∞ ] → [ 3 ; 4] , f (x) = x 2. Răspuns: 1. R - { -1, 1 } ; 2. A; 3. [ 1; 3 ] ; 4. A ; 5. [ , 2]

Ex. 2. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. A F 1. Funcţia f : R → R , f(x) = sin 5 x este periodică cu perioada principală T 0 = A F 2. Funcţia f : R → R , f(x) = cos 2 x este periodică cu perioada principală T 0 = π A F 3. Funcţia f : R-{ ( 2 k+1) / k Є Z }→ R , f (x) = tgx + sin 2 x este periodică cu perioada principală T 0 = 2π Răspuns: Adevărate 1 şi 2

Ex. 3. Disciplina / Clasa / Capitolul : Algebră / Clasa a X –a / Combinatorică Obiectivul: Elevul va fi capabil să stabilească proprietăţi ale coeficienţilor unei dezvoltări. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. Se consideră dezvoltarea : ( 1+x+x 2)13 = a 0 + a 1 x + ………. . a 26 x 26. Atunci : A F 1. a 0+a 1+a 2+ …. . +a 26 = 213 A F 2. a 0+a 1+a 2+ …. . +a 26 = 313 A F 3. a 0+a 1+a 4+ …. . +a 26 = A F 4. a 3= Răspuns: Adevărate 2, 3 şi 4

Ex. 4. Disciplina / Clasa/ Capitolul : Algebră/Cl. a. XII–a/Polinoame cu coeficienţi complecşi Obiectivul: Elevul va fi capabil să cunoască natura rădăcinilor unui polinom cu coeficienţi complecşi. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. Se consideră polinomul f = X 3 + (i+3)X 2 + (2+3 i)X + 6 Є C [X]. Atunci rădăcini ale polinomului f sunt : A F 1. x = i A F 2. x = - i A F 3. x = 3 A F 4. x = -3

Ex. 5. Disciplina / Clasa / Capitolul : Analiză matematică / Clasa a XI –a / Numere reale Obiectivul : Elevul va fi capabil să aplice inegalităţi importante referitoare la funcţii trigonometrice. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. A F 1. Dacă , atunci au loc inegalităţile: A F 2. Dacă , atunci au loc inegalităţile: Răspuns: Adevărată 2

Ex. 6. Disciplina / Clasa / Capitolul: Analiză matematică/Cl. a XII – a / Funcţii integrabile Obiectivul: Elevul va fi capabil să calculeze integrale folosind substituţii trigonometrice. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. Valoarea integralei este: A F 1. A F 2. Rezolvare : Facem substituţia x = 3 cost=φ(t) , φ: [0, π/2] → [0, 3] este derivabilă cu derivata continuă φ I (t) = - 3 sint , φ (o) = 3, φ (π/2) = 0 deci

Ex. 7. Disciplina / Clasa / Capitolul: Analiză matematică / Cl. a XII – a / Inele şi corpuri. Obiectivul: Elevul va fi capabil să determine divizorii proprii ai unui polinom dat cu coeficienţi dintr-un corp finit. Enunţ: Dacă apreciezi că afirmaţia este adevărată, încercuieşte litera A. În caz contrar încercuieşte litera F. Polinomul f = X 4+1 є Z 5[X] este : A F 1. reductibil A F ireductibil Răspuns: Adevărată 1.
![2 Tehnica perechilor Descriere şi utilizare I Neacşu A Stoica 1996 Tehnica perechilor 2. Tehnica perechilor Descriere şi utilizare [I. Neacşu, A. Stoica , 1996] Tehnica perechilor](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-26.jpg)
2. Tehnica perechilor Descriere şi utilizare [I. Neacşu, A. Stoica , 1996] Tehnica perechilor solicită din partea elevilor stabilirea unor corespondenţe între cuvinte, propoziţii, fraze, numere, litere sau alte categorii de simboluri , distribuite pe două coloane. Elementele din prima coloană , denumite premise, constituie enunţul itemului, iar cele din coloana a doua reprezintă răspunsurile. Criteriul sau criteriile de bază cărora se stabileşte răspunsul corect sunt enunţate/ explicitate în instrucţiunile care preced coloanele de premise şi de răspunsuri. Utilizarea se limitează la măsurarea abilităţii de a identifica relaţia existentă între două categorii. termeni – definiţii; simboluri – concepte; reguli – exemple; metode – exemplificări.

Cerinţe de proiectare a) să includă un număr inegal de răspunsuri şi premise, iar elevii să fie instruiţi că fiecare răspuns poate fi folosit o dată, de mai multe ori sau niciodată; b) lista răspunsurilor să fie angajată într-o ordine logică (de exemplu: ordinea albabetică pentru răspunsuri care presupun exprimarea în cuvinte sau ordinea crescătoare/descrescătoare pentru răspunsuri numerice). Această cerinţă vizează eliminarea furnizării oricăror indicii care ar putea conduce elevul spre „ghicirea” răspunsului corect; c) toate premisele şi răspunsurile unui item de acelaşi tip să fie plasate pe aceeaşi pagină.

Avantaje şi limite Tehnica permite abordarea unui foarte important volum de rezultate de învăţare într-un interval de timp redus, cu utilizarea eficientă a spaţiului pe foile de test, cât şi cu utilizarea eficientă a timpului profesorului la notare. Uşurinţa construcţiei itemilor este de asemenea un avantaj frecvent menţionat în legătură cu această tehnică, cu toate că este probabil mai corect să spunem că este mai uşor de construit un item de calitate slabă decât unul de bună calitate. Tehnica nu poate fi utilizată pentru abordarea unor rezultate de învăţare complexe, fiind de asemenea dificil, în unele cazuri să construim liste de premise sau de răspunsuri care să fie omogene.

Exemple de itemi Ex. 1. Disciplina / Clasa / Capitolul: Algebră / Clasa a IX-a / Funcţii Obiectivul: Elevul va fi capabil să aplice proprietăţile funcţiilor învăţate. Enunţ: Se dă o listă de funcţii şi un tabel în care pe prima coloană sunt scrise proprietăţi ale acestora. Marchează cu X căsuţele corespunzătoare proprietăţilor adevărate.

Funcţia Proprietatea Funcţia este crescătoare Funcţia este strict crescătoare Funcţia este descrescătoare Funcţia este strict descrescătoare Funcţia este monotonă Funcţia este injectivă Funcţia este surjectivă Funcţia este bijectivă Funcţia este pară Funcţia este impară Funcţia nu este nici pară, nici impară

Ex. 2. Disciplina / Clasa / Capitolul: Algebră / Clasa a XII-a / Polinoame cu coeficienţi complecsi Obiectivul: Elevul va fi capabil să stabilească polinoamele ireductibile dintr-o listă dată de polinoame , utilizând principii cunoscute de ireductibilitate Enunţ: Înscrie în spaţiul din stânga fiecărei proprietăţi polinomul din a doua coloană ce corespunde acestuia. ___ 1. polinomul este ireductibil în Z[X] ______ 2. polinomul este ireductibil în Q[X] ______ 3. polinomul este ireductibil în R[X] ______ 4. polinomul este ireductibil în C[X]

f = X 2 – 2 g = X 2 + X + 1 h = X 3 + X p = X 4 + X 3 + X 2 + X + 1 q = 2 X + 3 Răspuns: 1. f, g, p, q. 2. f, g, p, q. 3. g, q 4. q

Ex. 4. Disiplina / Clasa / Capitolul: Analiză matematică/ Clasa a XII –a / Funcţii integrabile. Obiectivul: Elevul va fi capabil să determine punctele de continuitate ale unei funcţii date pentru a preciza ce proprietăţi are aceasta. Enunţ: Înscrie în spaţiul din stânga fiecărei proprietăţi date funcţia din a doua coloană ce are proprietatea respectivă. _______ 1. funcţia este continuă _______ 2. funcţia admite primitive _______ 3. funcţia este monotonă _______ 4. funcţia este integrabilă _______ 5. funcţia are proprietatea Darboux
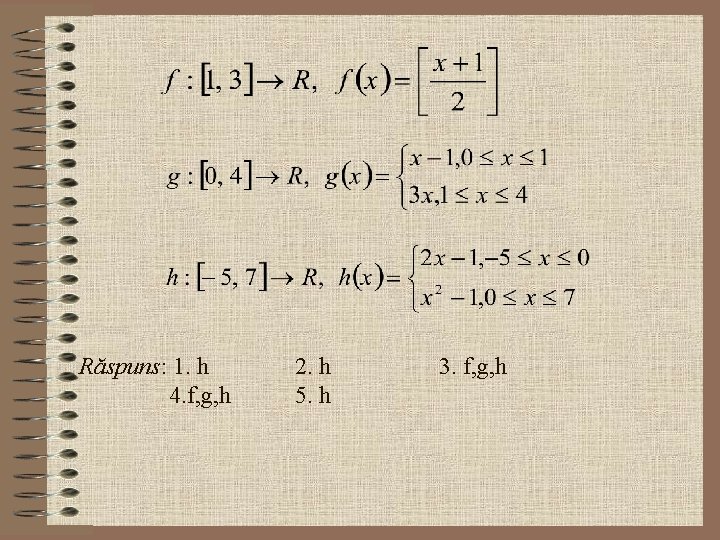
Răspuns: 1. h 4. f, g, h 2. h 5. h 3. f, g, h
![3 Tehnica alegerii multiple Descrierea şi utilizarea I Neacşu A Stoica 1996 Itemii 3. Tehnica alegerii multiple Descrierea şi utilizarea [I. Neacşu, A Stoica , 1996] Itemii](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-35.jpg)
3. Tehnica alegerii multiple Descrierea şi utilizarea [I. Neacşu, A Stoica , 1996] Itemii cu alegere multiplă solicită elevul să aleagă un răspuns dintr-o listă de variante oferite pentru o singură premisă. Elevul doar selectează un răspuns dintre cele care i se propun, nu creează el unul! Acest tip de itemi presupune, prin urmare, existenţa unei premise şi a unei liste de variante / opţiuni ( lista de variante reprezintă soluţiile itemului respectiv, sub forma unor cuvinte, numere simboluri sau fraze ). Elevul trebuie să aleagă singur răspunsul corect sau cea mai bună variantă. Celelalte răspunsuri, în afara celui corect, se numesc distractori ( variante incorecte, dar plauzibile şi paralele).

Itemii cu alegere multiplă pot fi utilizaţi pentru : - măsurarea rezultatelor învăţării, a cunoştinţelor asimilate pentru: v Cunoaşterea terminologiei; v Cunoaşterea elementelor: formule, proprietăţi, reguli; v Cunoaşterea metodelor -măsurarea rezultatelor învăţării ca reflectare a nivelului comprehensiv şi aplicativ: v Abilitatea de a aplica teoria în rezolvarea problemelor; v Abilitatea de a interpreta relaţia cauză – efect; v Abilitatea de a justifica alegerea metodelor şi procedeelor folosite;

Exemple de itemi Ex. 1. Disciplina / Clasa / Capitolul: Algebră / Clasa a IX-a / Mulţimi şi funcţii Obiectivul: Elevul va fi capabil să recunoască injectivitatea şi surjectivitatea unei funcţii Enunţ: Fie f : R → R , f(x) = x 7 + x + 2 , atunci : a) f este injectivă b) f nu este injectivă c) f este surjectivă d) f nu este surjectivă e) f este bijectivă şi f -1 (2) = 0 Încercuieşte literele corespunzătoare afirmaţiilor adevărate. Răspuns: Sunt adevărate afirmaţiile : a), c), e).

Notăm g(x) = x 7 şi h (x) = x + 2. Funcţiile sunt strict crescătoare şi f = g + h f strict crescătoare f injectivă. Fie Cum orice polinom de grad impar cu coeficienţi reali are cel puţin o rădăcină reală, rezultă că există cu f(x 0) = y, deci f surjectivă; f(0) = 2 f -1 (2) = 0.

Ex. 2. Disciplina / Clasa / Capitolul: Analiză matematică / Clasa a XI-a / Funcţii continue Obiectivul: Elevul va fi capabil să stabilească dacă o funcţie dată este continuă. Enunţ: Stabiliţi care din următoarele funcţii sunt uniform continue pe intervalele indicate: a) f(x) = x 3 pe [0 ; 1] b) f(x) = x 3 pe (0 ; 1) c) f(x) = x 3 pe R d) pe (0 ; 1) e) pe (0 ; 1) f) pe ( 0; 1 ] g) f(x) = tg x pe [0; π/4]

h) f(x) = tg x pe [0; π/2) i) pe ( 0 ; π/2) j ) pe ( 0 ; 3) k) pe ( 4 ; + ∞ ) Răspuns: Sunt uniform continue funcţiile definite la punctele: a), b), f), g), i), k).

Ex. 4. Disciplina / Clasa / Capitolul: Algebră / Clasa a XII –a / Inele şi corpuri Obiectivul: Elevul va fi capabil să determine elementele inversabile într-un inel de clase de resturi. Enunţ: În monoidul ( Z 9 , ) notăm A. ( U (Z 9) , · ) este monoid şi nu este grup B. (U (Z 9) , · ) este grup C. D. (U(Z 9), ·) ( S 3 , · ) E. (U(Z 9), ·) ( S 6 , + ). Încercuieşte literele corespunzătoare afirmaţiilor corecte : Răspuns: Sunt corecte afirmaţiile B, C, E. Є Z 9 este inversabilă (a, 9) = 1 . Grupul ( S 3 , ·) este necomutativ, iar grupul ( U(Z 9), · ) este comutativ.
![Tehnici de testare Itemi semiobiectivi Descriere I Neacsu A Stoica 1996 Tehnici de testare – Itemi semiobiectivi Descriere [ I. Neacsu, A. Stoica, 1996 ]](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-42.jpg)
Tehnici de testare – Itemi semiobiectivi Descriere [ I. Neacsu, A. Stoica, 1996 ] Prin concizia răspunsului pe care un elev este solicitat să răspundă la un item semiobiectiv , se dezvoltă: 1) profunzimea înţelegerii noţiunilor învăţate; 2) operarea cu noţiuni matematice într-un ritm mai alert decât a fost obişnuit până acum; 3) claritate în exprimare.

Timpul necesar de rezolvare în general a itemilor semiobiectivi fiind redus faţă de itemii cu răspuns deschis, se pot aplica în aceeaşi unitate de timp (de testare a elevului) un număr mai mare de itemi prin care verificăm o cantitate mai mare de cunoştinţe şi capacităţi pe care elevii le posedă. Gradul de dificultate în cadrul fiecărui item trebuie să fie crescător ceea ce duce la o apropiere de acesta a unui număr mai mare de elevi. Itemii semiobiectivi sunt de tipul : - întrebări cu răspuns scurt / de completare - întrebări structurate

Itemi cu răspuns scurt / de completare Descriere: Itemii cu răspuns scurt / de completare sunt cei prin care elevului i se cere să ofere un răspuns (scurt) în totalitatea lui sau o parte componentă a unei afirmaţii, astfel încât aceasta să capete sens şi valoare de adevăr. - răspunsul cerut elevului este limitat, ca spaţiu, formă şi conţinut, de structura întrebării; - sarcina este puternic structurată; - libertatea elevului de o reorganiza informaţia primită şi de a oferi răspunsul în forma dorită este redusă; - pentru a oferi răspunsul corect, elevul trebuie să demonstreze nu numai cunoaşterea, dar şi abilitatea de a structura, elabora cel mai potrivit şi scurt răspuns

Itemii cu răspuns scurt le cer elevilor să ofere răspunsul sub forma unei propoziţii, fraze, a unui cuvânt, număr, simbol. Itemii de completare solicită, în general, drept răspuns doar unul sau două cuvinte, care uneori să se încadreze în contextul – suport oferit. Diferenţa de formă a cerinţei este aceea că în primul caz se foloseşte o întrebare directă, iar în al doilea o informaţie incompletă.

Exemple de itemi Ex. 1. Disciplina / Clasa / Capitolul: Matematică / Clasa a IX-a / Ecuaţii trigonometrice Obiectivul: Elevul să determine imaginea unei funcţii trigonometrice date. Enunţ: Completează spaţiile punctate astfel încât să obţii afirmaţii adevărate Funcţia f : R → R, f(x) = sinx +cosx admite pe ………… ca minim şi pe …………. ca maxim. a) Ecuaţia nu are soluţii deoarece …… b) Ecuaţia are soluţie deoarece ……

Rezolvare: , deci şi . a) Cum , ecuaţia dată nu are soluţii. b)

Ex. 2. Disciplina / Clasa / Capitolul: Analiză matematică / Clasa a XI-a / Şiruri Obiectiv: Elevul va fi capabil să reproducă rezultatele de bază ale capitolului Şiruri reale. Enunţ: Completează spaţiile punctate astfel încât să obţii afirmaţii adevărate: 1) Orice şir convergent este. . . . . 2) Orice şir monoton are. . . . . 3) Orice şir nemărginit este. . . . . 4) Orice subşir al unui şir ce are limită are. . . . 5) Dacă un şir conţine două subşiruri ce au limite diferite, atunci. . . . 6) Orice şir monoton şi mărginit este. . . . . Răspuns: 1) mărginit. 2) limită. 3) divergent 4) aceeaşi limită. 5) şirul nu are limită. 6) Convergent

Ex. 3. Disciplina / Clasa / Capitolul: Matematică / Clasa a XII-a / Inele Obiectivul: Elevul va fi capabil să aplice operaţiile de adunare şi înmulţire cu clase de resturi într-o structură algebrică cunoscută. Enunţ: Completează spaţiile punctate astfel încât să obţii afirmaţii adevărate : Structura algebrică reprezentată de tripletul este. . . Rezolvând în Z 8 ecuaţia: obţinem soluţia. . . Răspuns: Inelul este comutativ şi unitar.
![Întrebări structurate Descriere Stoica A coordonator 1996 O întrebare structurată este formată Întrebări structurate Descriere [ Stoica A. ( coordonator) 1996] O întrebare structurată este formată](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-50.jpg)
Întrebări structurate Descriere [ Stoica A. ( coordonator) 1996] O întrebare structurată este formată din mai multe subîntrebări – de tip obiectiv sau semiobiectiv – legate între ele printr-un element comun. Există spaţiu gol între tehnicile de evaluare cu răspuns liber şi cele cu răspuns limitat impuse de itemii obiectivi. Acest gol poate fi acoperit prin utilizarea întrebărilor structurate.

Exemple de itemi Ex. 1. Disciplina / Clasa /Capitolul: Algebră / Clasa a IX-a / Funcţia de gradul al doilea Obiectivul: Elevul va fi capabil să determine mulţimi cu condiţii date. Enunţ: Fie M o mulţime de numere reale cu proprietăţile : a) b) c) Se cer : 1) Să se determine o ecuaţie cu coeficienţi întregi care are rădăcina a. 2) Demonstraţi că

Rezolvare : 1) Ridicând la pătrat obţinem : Ridicăm la pătrat şi obţinem 2) . Folosind proprietăţile a) , b) , c) , şi ultima relaţie obţinem că Deci şi

Ex. 2. Disciplina/ Clasa / Capitolul: Algebră / Clasa a IX-a/ Funcţii Obiectivul: Elevul va fi capabil să aplice proprietăţi ale funcţiilor. Enunţ: Fie funcţia f: R → R cu proprietatea şi mulţimea . a) Să se arate că şi f(R) = M. b) Dacă atunci g este bijecţie. c) Daţi exemplu de funcţie f care verifică ipoteza şi care nu este bijecţie, apoi determinaţi mulţimea M şi restricţia g a funcţiei f la M.

Rezolvare: a) Fie şi Fie atunci deci , adică . b) Fie , deci g este injectivă. Fie deci g este surjectivă c) f nu este bijectivă M={0} şi g : M→M , g(0) = 0 este bijectivă.

Ex. 3. Disciplina/ Clasa /Capitolul: Algebră / Clasa a IX-a / Inducţie matematică Obiectivul: Elevul va fi capabil să aplice o variantă a principiului inducţiei matematice Enunţ: a) Daţi un exemplu de număr iraţional z pentru care b) Dacă şi , atunci ; c)Dacă z este număr iraţional şi există astfel încât să fie iraţional , atunci este iraţional.

Rezolvare: a)Rezolvăm ecuaţia . Numărul şi b) Se demonstrează cu ajutorul variantei a II-a a inducţiei matematice. Pentru n = 1 avem Presupunem că c) Dacă , conform punctului b) rezultă contradicţie. Deci .
![Tehnici de testare Itemi subiectivi Descriere I Neacşu A Stoica 1996 Itemii subiectivi Tehnici de testare – Itemi subiectivi Descriere [I. Neacşu, A. Stoica, 1996] Itemii subiectivi,](https://slidetodoc.com/presentation_image/0fb42b91f1e556ce21eee6aa92d9eba8/image-57.jpg)
Tehnici de testare – Itemi subiectivi Descriere [I. Neacşu, A. Stoica, 1996] Itemii subiectivi, sau cu răspuns deschis, reprezintă forma „tradiţională” de evaluare în ţara noastră. Ele sunt relativ uşor de construit şi testează obiective ce scot în evidenţă originalitatea, creativitatea şi caracterul personal al răspunsului. Itemii cu răspuns deschis presupun: - rezolvarea de probleme; - eseu structurat sau liber (mai puţin la matematică)

Rezolvarea de probleme Descriere şi caracteristici Rezolvarea de probleme este o activitate curentă a procesului de instruire. Capacitatea de a rezolva probleme se dezvoltă prin exerciţiu de-a lungul unei perioade mai lungi. Obiective urmărite: -înţelegerea problemei; -obţinerea informaţiilor necesare rezolvării problemei; -formularea şi testarea ipotezelor; -descrierea metodelor de rezolvare a problemei; -elaborarea unui scurt raport despre rezultatele obţinute; -posibilitatea de generalizare şi transfer a tehnicilor de rezolvare

Avantaje: -permite formarea unei gândiri productive; -oferă posibilitatea unei interdependenţe; -dă posibilitatea de discuţie asupra diverselor metode şi soluţii; -activează atitudinea critică şi învaţă pe elevi să aprecieze metoda cea mai bună de lucru; -oferă posibilitatea analizei erorilor. Dezavantaje: -necesită un timp lung de proiectare; -implică resurse materiale uneori costisitoare; -necesită un timp mare de administrare şi complexitate a sarcinii; -dacă se doreşte notarea fiecărui elev, aceasta trebuie făcut nuanţat.

Exemple de itemi Ex. 1. Disciplina / Clasa / Capitolul: Algebră / Clasa a IX-a / Funcţii Obiectivul: Elevul va fi capabil să determine un punct fix al unei funcţii date printr-o relaţie funcţională. Enunţ: Fie funcţia f: R→R astfel încât Să se arate că există R cu proprietatea că f(c) = c.

Rezolvare şi barem de notare: Aplicăm pe f ambilor membrii şi obţinem : (se acordă 5 puncte). În particular pentru obţinem Deci este punct fix al lui f. (se acordă 5 puncte).

Ex. 2. Disciplina / Clasa / Capitolul: Matematică / Clasa a XII-a / Polinoame cu coeficienţi complecşi Obiectivul: Elevul va fi capabil să aplice teorema fundamentală a algebrei şi să rezolve o ecuaţie binomă dată. Enunţ: Studiaţi injectivitatea şi surjectivitatea funcţiei f: C →C definită prin . Rezolvaţi ecuaţia f(z) = 1 + i Rezolvare: z 3 = 1 are soluţiile , şi ( 3 puncte)

f(1) = f (ε 1) = 1 deci f nu este injectivă ( 1 punct) Fie , ecuaţia z 3 – y = 0 are cel puţin o soluţie datorită teoremei fundamentale a algebrei ( 1 punct) Rezultă f surjecţie. ( 1 punct) ( 2 puncte) Soluţiile : , . ( 2 puncte)

Ex. 3. Disciplina / Clasa / Capitolul: Algebră / Clasa a XI-a / Matrici Obiectivul: Elevul va fi capabil să calculeze puterea n-a a unei matrice de o formă specială. Enunţ: Fie . Determinaţi astfel ca şi calculaţi .

Rezolvare: deci putem lua λ = 2 şi sau . Din , rezultat demonstrat prin inducţie matematică. Se acordă 10 puncte.

Ex. 4. Disciplina / Clasa / Capitolul: Algebră / Clasa a XII-a / Grupuri Obiectivul: Elevul va fi capabil să stabilească dacă două grupuri date sunt sau nu izoforme. Enunţ: Să se arate că grupurile aditive Q şi Q X Q nu sunt izomorfe. Rezolvare: Presupunem că Q ≈ Q X Q, deci există f : Q → Q X Q un izomorfism de grup : f (1) = (a , b ) Q X Q. (2 puncte) f(2) = f ( 1 + 1) = f(1) + f(1) = ( 2 a, 2 b) ( 1 punct)

Prin inducţie se arată că: , deci Z (2 puncte) Fie adică (2 puncte) Dacă a = 0 sau b = 0 evident f nu este surjectivă. (1 punct) Dacă a ≠ 0 şi b ≠ 0 fie Q XQ . Cum f este surjectivă rezultă că există astfel încât şi , adică α şi β nu sunt independente. Deci f nu e surjectivă , contradicţie. (2 puncte)

Metode alternative de evaluare Investigaţia - elevul este pus în situaţia de a căuta o soluţie deosebită (faţă de soluţiile algoritmice). Proiectul – evaluare complexă desfăşurată pe o perioadă de timp mai lungă; - cuprinde două etape: - colectarea datelor; - realizarea efectivă a proiectului. - are un caracter practic mult mai accentuat. Portofoliul – prin care se urmăreşte progresul realizat într-un semestru sau un an şcolar, dar şi atitudinea sa faţă de disciplină.

Autoevaluarea - permite aprecierea propriilor performanţe în raport cu obiectivele operaţionale. În procesul autoevaluării elevul va înţelege mai bine obiectivele şi conţinutul sarcinii ce o are de rezolvat, căile prin care se găseşte soluţia corectă şi modul în care efortul său de rezolvare a sarcinii este valorificat. Autoevaluarea trebuie făcută sub atenta îndrumare a profesorului în special la clasele de liceu.

Bibliografie: 1. 2. 3. 4. 5. 6. Neacşu, A. Stoica, . . . – ”Ghid general de evaluare şi examinare”, Bucureşti, 1996, Editura “Aramis” A. Stoica (coord. ) -“Ghid practic de elaborare a itemilor pentru examene”, ISE, Bucureşti, 1996 M. Becheanu, . . . - “Probleme de algebră, analiză şi geometrie”, Ed. “Cartea românească”, Bucureşti, 1991 I. D. Ion, A. Ghioca, N. I. Nediţă, N. Angelescu “Algebra- cl. a XII-a”, Ed. “Paralela 45”, Piteşti, 1997 Virgil Nicula- “Numere comlexe”, Ed. Scorpion 7”, Bucureşti, 1993 C. Năstăsescu, C. Niţă, M. Brandiburu, D. Joiţa “Culegere de probleme de algebră pentru liceu”, Ed. “Roteh-Pro”, 1996

7. L. Panaitopol, M. E. Panaitopol, M. Lascu- “Inducţie matematică”, Ed. “GIL”, Zalău 8. V. Arsinte- “Probleme elementare de calcul integral”, Ed. Universităţii Bucureşti, 1995 9. M. Nicolescu, S. Marcus, N. Dinculeanu – “Analiza matematică”, Vol I. , Ed. Didactică şi Pedagogică, Bucureşti, 1980 10. M. Dincă, M. Chiriţă –”Numere complexe în matematica de liceu”, Ed. “ALL”, Bucureşti, 1995 11. D. Brânzei, S. Aniţa, M. Chirciu – “Geometrie, cl. a IX-a”, Ed. Paralela 45”, Piteşti, 1996.

CERCUL PEDAGOGIC AL PROFESORILOR DE MATEMATICĂ 19. Noiembrie 2010 SF RŞIT
 Colegiul national silvania zalau
Colegiul national silvania zalau Krist jednom stade na žalu
Krist jednom stade na žalu Macierz żalu
Macierz żalu Evaluarea performantelor angajatilor model
Evaluarea performantelor angajatilor model Metode de evaluare moderne
Metode de evaluare moderne Evaluarea online avantaje si dezavantaje
Evaluarea online avantaje si dezavantaje Analiza swot evaluare initiala
Analiza swot evaluare initiala Evaluarea documentelor
Evaluarea documentelor Raspunderea in afaceri se refera la
Raspunderea in afaceri se refera la Evaluarea criteriala
Evaluarea criteriala Evaluarea copiilor prescolari
Evaluarea copiilor prescolari Evaluarea functionarilor publici
Evaluarea functionarilor publici Monitorizarea si evaluarea unui proiect erasmus
Monitorizarea si evaluarea unui proiect erasmus Nevoia de a se misca si a avea o buna postura
Nevoia de a se misca si a avea o buna postura Henri coanda biografie
Henri coanda biografie Liceul lia galati
Liceul lia galati Cuza ploiesti
Cuza ploiesti Colegiul energetic rm valcea
Colegiul energetic rm valcea Karpen bacau
Karpen bacau Colegiul agricol dimitrie petrescu caracal
Colegiul agricol dimitrie petrescu caracal Colegiul hermes
Colegiul hermes Colegiul ecologic alexandru ionescu pitesti
Colegiul ecologic alexandru ionescu pitesti Liceul tehnologic de industrie alimentara
Liceul tehnologic de industrie alimentara Gheorghe sincai baia mare
Gheorghe sincai baia mare Tiberiu maior cluj
Tiberiu maior cluj Liceul teoretic alexandru ioan cuza corabia
Liceul teoretic alexandru ioan cuza corabia Colegiul economic buzau
Colegiul economic buzau Danubiana roman
Danubiana roman Liceul economic arad
Liceul economic arad Colegiul grigore antipa bacau
Colegiul grigore antipa bacau Adriana radu colegiul national iasi
Adriana radu colegiul national iasi Colegiul national gheorghe sincai
Colegiul national gheorghe sincai Colegiul vladimir streinu
Colegiul vladimir streinu Colegiul national gheorghe asachi
Colegiul national gheorghe asachi Dorin teodorescu boala
Dorin teodorescu boala Colegiul national nicolae iorga
Colegiul national nicolae iorga Liceul ionita asan caracal profesori
Liceul ionita asan caracal profesori Liceul tehnologic transilvania baia mare
Liceul tehnologic transilvania baia mare Ce inseamna ucecom
Ce inseamna ucecom Camin nicolae titulescu preturi
Camin nicolae titulescu preturi Daniela nicoara piatra neamt
Daniela nicoara piatra neamt Colegiul national george baritiu cluj
Colegiul national george baritiu cluj Elena doamna galati
Elena doamna galati Enteromorpha
Enteromorpha Colegiul economic delta dunarii tulcea
Colegiul economic delta dunarii tulcea Colegiul tehnic matei corvin hunedoara
Colegiul tehnic matei corvin hunedoara Colegiul national gheorghe sincai
Colegiul national gheorghe sincai Programa de apoio ao aluno
Programa de apoio ao aluno Servicio de salud del reloncaví
Servicio de salud del reloncaví Programa recreativo ejemplo
Programa recreativo ejemplo Software landirenzo
Software landirenzo Formato plan de desarrollo individual
Formato plan de desarrollo individual Halimbawa ng tekstong may sanhi at bunga
Halimbawa ng tekstong may sanhi at bunga Matematikos bendroji programa
Matematikos bendroji programa Raspored programa doma tv
Raspored programa doma tv Es el programa de control maestro del ordenador
Es el programa de control maestro del ordenador Programa hdt
Programa hdt Programa de colombia compite
Programa de colombia compitePrograma cisco networking academy
 Modelo de consultor moderniza
Modelo de consultor moderniza Programa investigacion
Programa investigacion Como se hacen los programas de radio
Como se hacen los programas de radio Programa especial para la seguridad alimentaria
Programa especial para la seguridad alimentaria Programa dua
Programa dua Nombres para club de guías mayores
Nombres para club de guías mayores Stop seguridad industrial
Stop seguridad industrial Estructura de un programa en c
Estructura de un programa en c Pmg project management group
Pmg project management group Estructura de un programa
Estructura de un programa Programa dis
Programa dis Biologijos vertinimo lentele
Biologijos vertinimo lentele Pagsasagawa ng enhanced retail access for the poor
Pagsasagawa ng enhanced retail access for the poor Actividades de artes visuales para segundo básico
Actividades de artes visuales para segundo básico