COLEGIO PARROQUIAL MIXTO SAN PEDRO CHANEL SOCIEDAD DE

COLEGIO PARROQUIAL MIXTO “SAN PEDRO CHANEL” SOCIEDAD DE MARIA (PADRES MARISTAS) SULLANA Ecuaciones Cuadráticas Por: Jhony Sandoval Juárez Especialidad: Matemática 4 to “B”

DEFINICION: Una ecuación cuadrática es una ecuación en su forma reales y a es diferente de cero , donde a, b, y c son números EJEMPLOS a = 9, b = 6, c = 10 a = 3, b = -9, c = 0 a = -6, b = 0, c = 10 La ecuación se llama completa cuando tiene los tres términos a, b y c, es decir cuando estos términos son distintos de cero. La ecuación es incompleta si faltan las constante “b” ó “c”. Pero sí b=0, la ecuación recibe el nombre de ecuación pura.

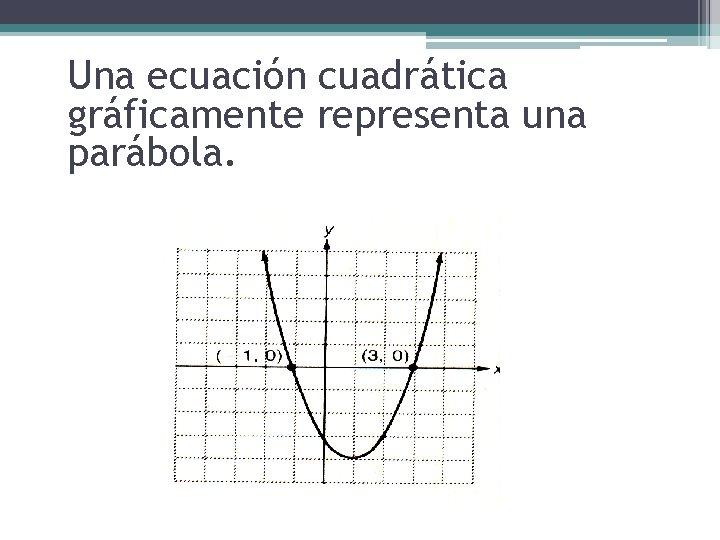
Una ecuación cuadrática gráficamente representa una parábola.

FORMAS DE SOLUCIONAR UNA ECUACION CUADRÁTICA • Hay tres formas de hallar las raíces ( el o los valores de la variable) de las ecuaciones cuadráticas: • 1. Factorización Simple 2. Completando el Cuadrados 3. Fórmula Cuadrática

Factorización Simple: La factorización simple consiste en convertir la ecuación cuadrática en un producto de binomios. Luego, se busca el valor de x de cada binomio. • Ejemplo: Realizar la factorización simple de la ecuación • a=1 b=2 c=-8 • • (x )=0 ( x + ) (x - ) = 0 4 y – 2 4 + -2 = 2 4 · -2 = -8 • (x + 4 ) (x – 2) = 0 • x+4=0 x– 2=0 • x+4=0 x=0– 4 x = -4 x– 2=0 x=0+2 x=2 Estas son las dos soluciones.

Completando Cuadrados: En este método, la ecuación tiene que estar en su forma ax 2+bx+c; y siempre la constante de a tiene que ser igual a 1. Para lograrlo hay que dividir a toda la ecuación por el valor de a así: Luego pasamos al otro miembro el valor de c/a y a la ecuación restante le sumaremos a ambos miembros el valor de: Por ejemplo, para factorizar la ecuación 4 x 2 + 12 x – 8 = 0, hay que despejar de la siguiente forma: Ahora, a= 1 .

Ahora la nueva ecuación será: Donde, a= 1, b= 3 y c= -2 Luego: Le sumamos a ambos miembros el (b/2)2 Finalmente la ecuación quedará: .

METODO DE LA FORMA GENERAL O CUADRÁTICA Este método es muy simple: hay que sustituir los valores de a, b y c de la ecuación cuadrática a la siguiente fórmula: Ejemplo: X 2 + 2 x – 8 = 0 x = -2 ± 6 2 X = -2 + 6 2 a = 1, b = 2, c = -8 x = -2 - 6 2 x=4 x = -8 2 2 x=-4

EL DISCRIMINANTE Como se vio anteriormente para resolver una ecuación cuadrática disponemos de la siguiente fórmula general Si llamamos D al discriminante de esta ecuación. Se concluye lo siguiente: D>0 La ecuación tiene 2 soluciones reales diferentes D=0 La ecuación tiene 2 soluciones reales iguales D<0 La ecuación tiene 2 soluciones complejas

Ecuaciones cuadráticas: PROPIEDADES DE LAS RAÍCES • En una ecuación de la forma ax 2 + bx + c = 0 • donde a = 0 , se tiene como raíces :

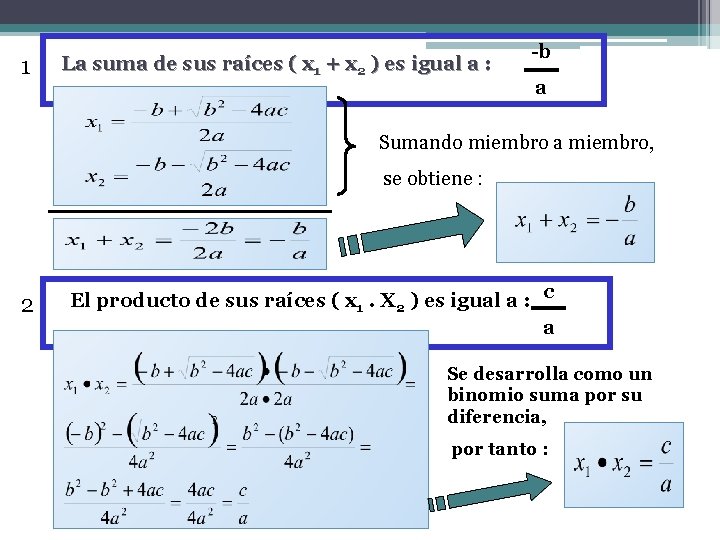
1 La suma de sus raíces ( x 1 + x 2 ) es igual a : -b a Sumando miembro a miembro, se obtiene : 2 El producto de sus raíces ( x 1. X 2 ) es igual a : c a Se desarrolla como un binomio suma por su diferencia, por tanto :

Determinación de la ecuación Si en la ecuación ax 2 + bx + c = 0 dividimos entre “a” la podemos transformar en : x 2 –(-b/a)x + c/a = 0 y por tanto reemplazar “–b/a” por la suma y “c/a” por el producto. x 2 – (x 1+x 2) x + (x 1. x 2) = 0

EJERCICIOS : 1. - Determina ( halla) la ecuación cuadrática cuyas raíces son 5 y -3 Recordar que la ecuación ax 2 + bx + c = 0 se puede transformar en : x 2 –(-b/a)x + c/a = 0 Si consideramos x 2 – (x 1+x 2) x + (x 1. x 2) = 0 a=1 será b = ( x 1+ x 2 ) = [ 5 +(-3)] = 2 será c = (x 1. X 2 ) = 5 ( -3 ) = - 15 Por tanto, la ecuación será : x 2 – 2 x – 15 = 0 Es conveniente recordar que en un trinomio como: x 2 + 5 x + 6 = 0, por la descomposición por método de aspa se cumple que b sale con la suma de factores y c con el producto de los mismos 2. - Determina la ecuación cuadrática cuyas raíces son 3/4 y 1/4 Será b = ( x 1 +x 2) = ( ¾ + ¼ ) = 4/4 = 1 Será c = (x 1. x 2 ) = ( ¾. ¼) = 3/16 Por tanto la ecuación será : x 2 – (1)x + 3/16 = 0 (se reduce a denominador común : 16 x 2 – 16 x + 3 = 0

ECUACIONES REDUCIBLES A CUADRÁTICAS • ECUACIONES RACIONALES FRACCIONARIAS • ECUACIONES IRRACIONALES (con RADICALES) • ECUACIONES POLINÓMICAS DE LA FORMA ax 4 + bx 2 + c = 0 (ecuaciones bicuadradas)

Ecuaciones racionales fraccionarias Son ecuaciones que al ser transformadas en otras equivalentes resultan ser cuadráticas. Ejemplo: Determinamos las restricciones Reducimos a denominador común y eliminamos denominadores Multiplicamos, reducimos y factorizamos (x – 8) (x + 2) = 0 por tanto x’ = 8 ; x” = -2 C. S. = { -2 ; 8 }

ECUACIONES IRRACIONALES Son ecuaciones donde la variable está afectada por un radical. Método para resolverlas * Se pasa a un miembro el término en que la incógnita esté bajo radical y al otro los demás términos. * Se elevan ambos miembros al cuadrado con el fin de hacer desaparecer los radicales y luego se procede como en los demás casos. * Se debe comprobar si las raíces halladas satisfacen a la ecuación inicial. EJEMPLO: Se ordena, se factoriza y se hallan las raíces Por tanto: x’ = 25 ; x” = 9 La raíz x” = 9 no satisface la ecuación inicial; se rechaza. C. S. = { 25 }

Otro ejemplo: Ecuación con 2 radicales. Se pasan ambos radicales a un miembro de la ecuación y el resto al otro, para proceder a elevar al cuadrado, y desarrollar. Habiendo quedado radical en el doble producto se repite el mismo proceso: se ordena, se eleva al cuadrado, se resuelve. Por tanto: x’ = 9 ; x” = 1 Al comprobar las raíces en la ecuación original, las 2 sirven. . C. S. ={1; 9}

ECUACIONES BICUADRADAS Son ecuaciones de cuarto grado : ax 4 + bx 2 + c = 0 ; No contienen más que las potencias pares de la incógnita. Para resolverlas se hace un cambio de variable. El número de soluciones lo determina el grado de la ecuación (4). EJEMPLO : (y - 4)(y - 9) = 0 y=4 y resolvemos; por tanto: y = 9 Como habíamos hecho x 2 = y lo reemplazamos y resolvemos Por tanto : C. S. = {-3; -2; 2; 3 }