Cold Melting of Solid Electron Phases in Quantum

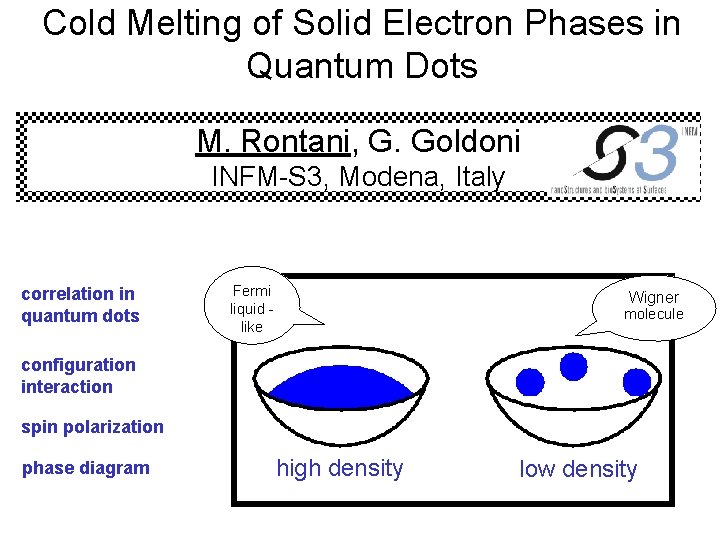
Cold Melting of Solid Electron Phases in Quantum Dots M. Rontani, G. Goldoni INFM-S 3, Modena, Italy correlation in quantum dots Fermi liquid like Wigner molecule configuration interaction spin polarization phase diagram high density low density

Why quantum dots? potential for new devices single-electron transistor, laser, single-photon emitter laboratory to explore fundamentals of few-body physics quantum control of charge and spin degrees of freedom easy access to different correlation regimes

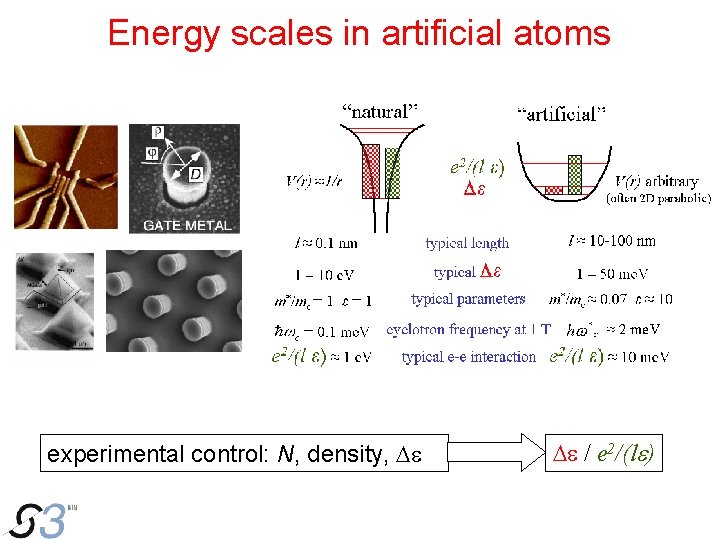
Energy scales in artificial atoms experimental control: N, density, De De / e 2/(le)

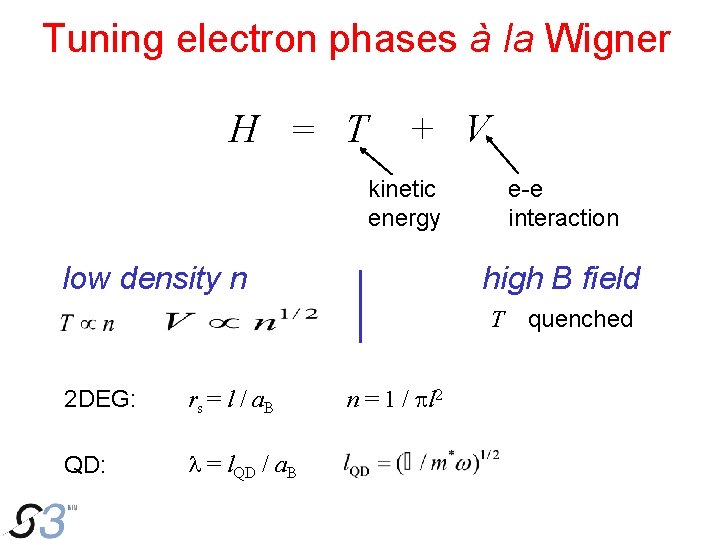
Tuning electron phases à la Wigner H = T + V kinetic energy low density n e-e interaction high B field T 2 DEG: rs = l / a. B QD: l = l. QD / a. B n = 1 / pl 2 quenched

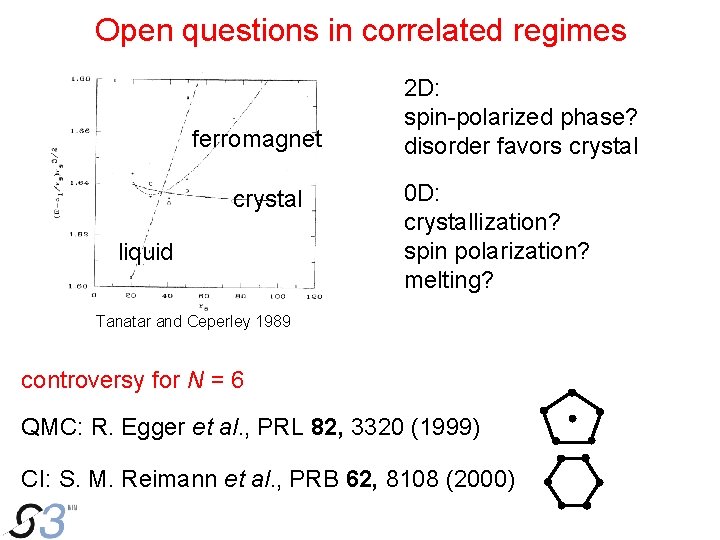
Open questions in correlated regimes ferromagnet crystal liquid 2 D: spin-polarized phase? disorder favors crystal 0 D: crystallization? spin polarization? melting? Tanatar and Ceperley 1989 controversy for N = 6 QMC: R. Egger et al. , PRL 82, 3320 (1999) CI: S. M. Reimann et al. , PRB 62, 8108 (2000)

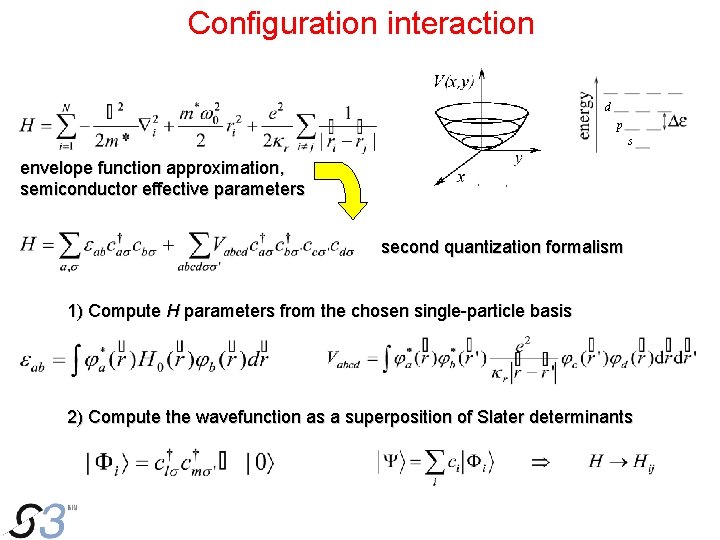
Configuration interaction d p s envelope function approximation, semiconductor effective parameters second quantization formalism 1) Compute H parameters from the chosen single-particle basis 2) Compute the wavefunction as a superposition of Slater determinants

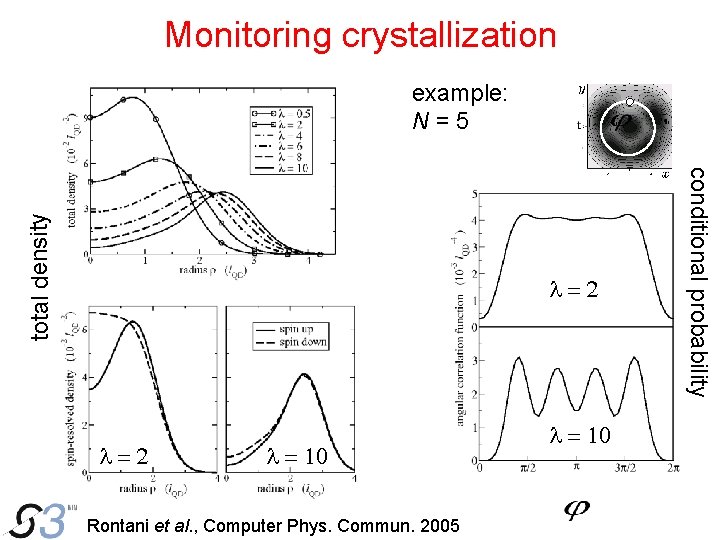
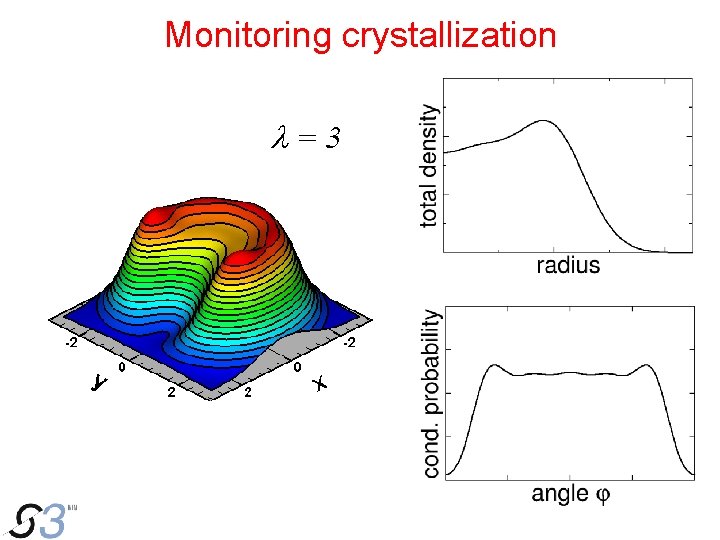
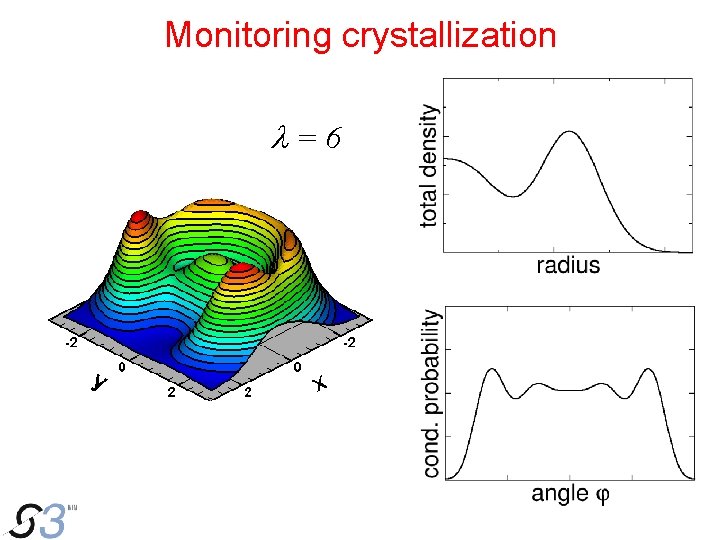
Monitoring crystallization l=2 l = 10 Rontani et al. , Computer Phys. Commun. 2005 l = 10 conditional probability total density example: N=5

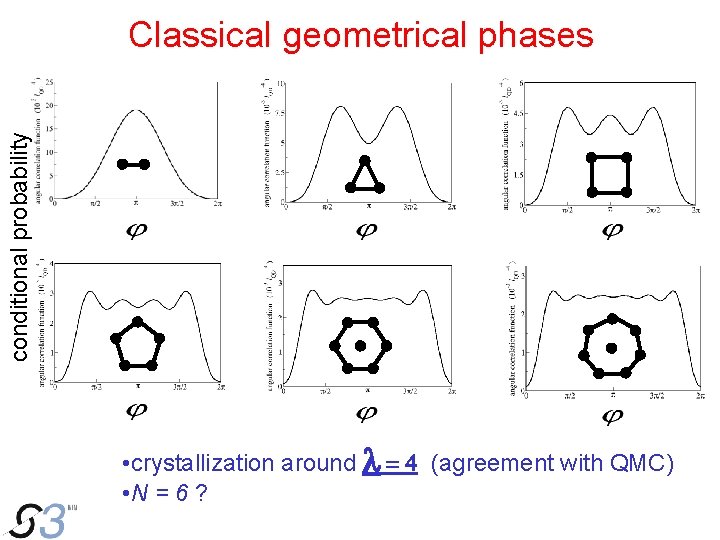
conditional probability Classical geometrical phases • crystallization around l = 4 (agreement with QMC) • N = 6 ?

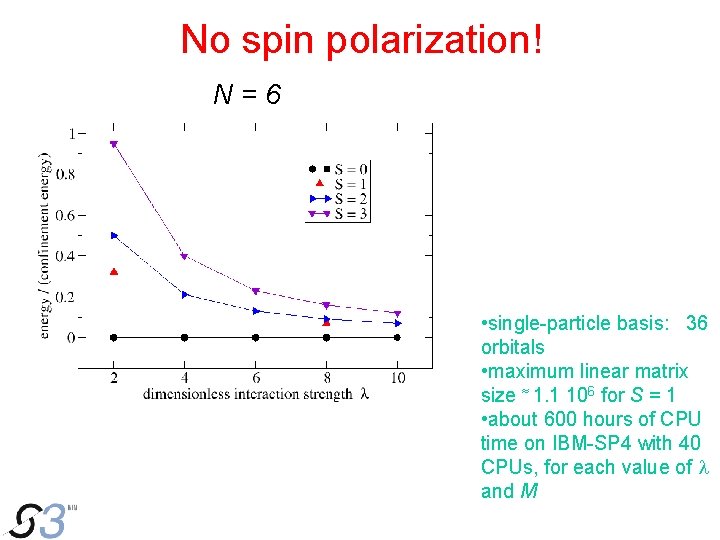
No spin polarization! N=6 • single-particle basis: 36 orbitals • maximum linear matrix size ≈ 1. 1 106 for S = 1 • about 600 hours of CPU time on IBM-SP 4 with 40 CPUs, for each value of l and M

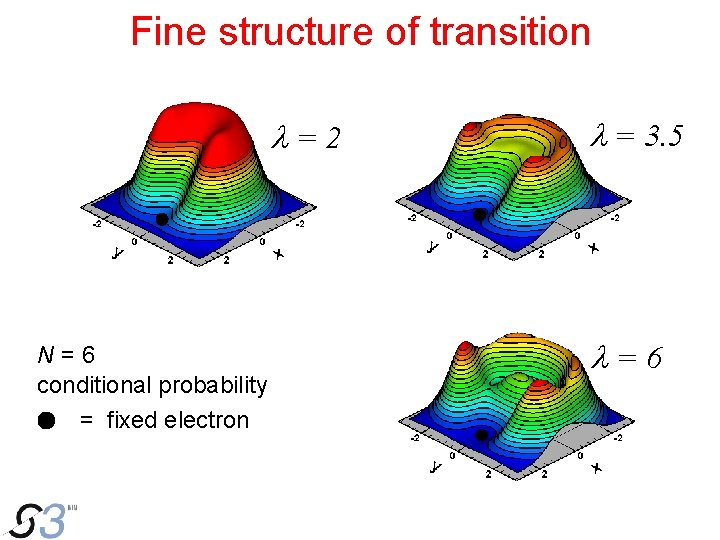
Fine structure of transition l=2 N=6 conditional probability = fixed electron l = 3. 5 l=6

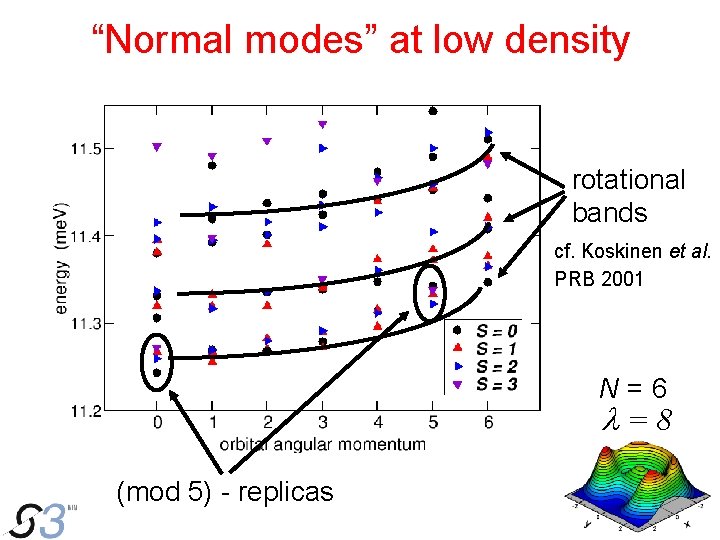
“Normal modes” at low density rotational bands cf. Koskinen et al. PRB 2001 N=6 l=8 (mod 5) - replicas

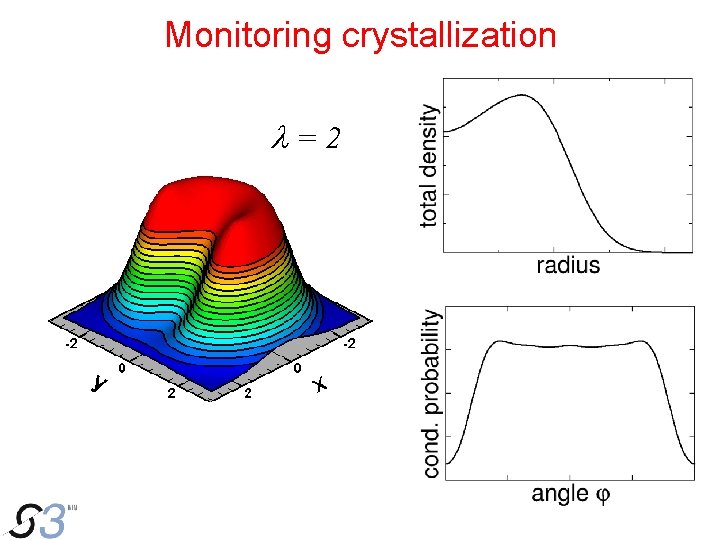
Monitoring crystallization l=2

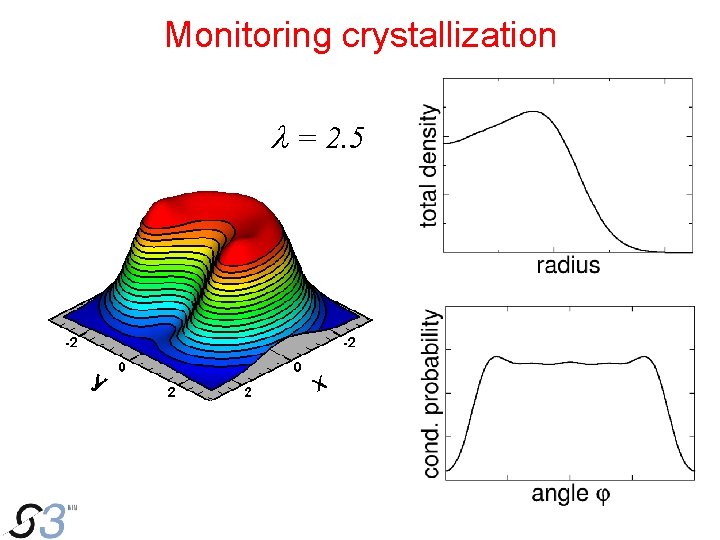
Monitoring crystallization l = 2. 5

Monitoring crystallization l=3

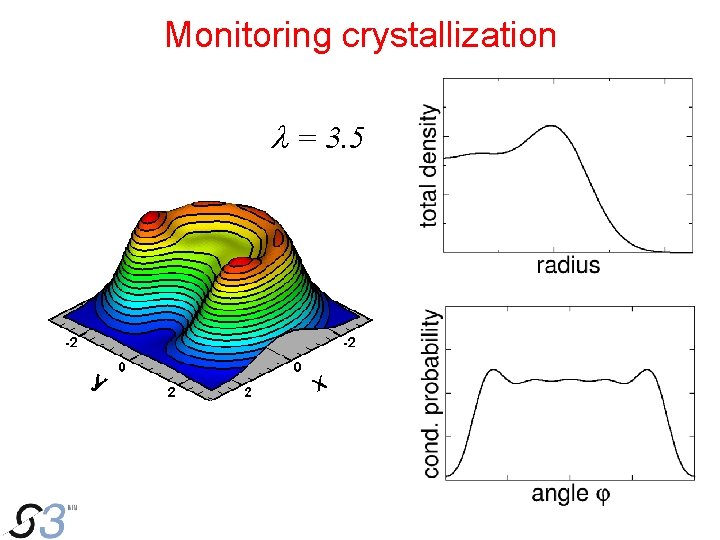
Monitoring crystallization l = 3. 5

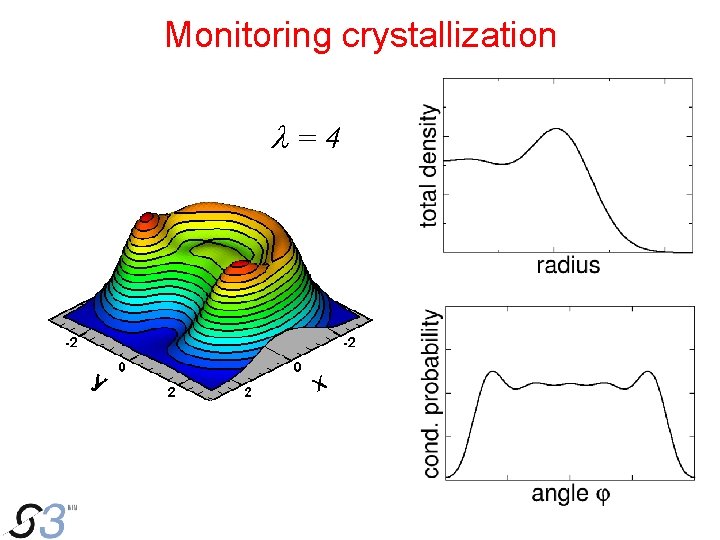
Monitoring crystallization l=4

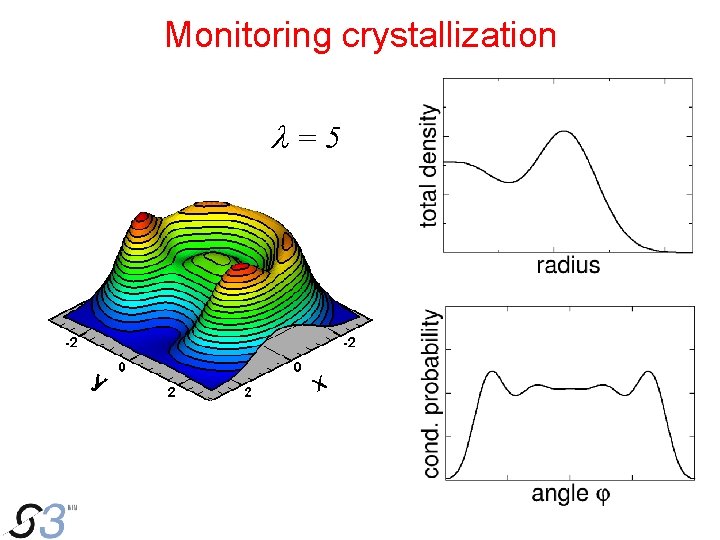
Monitoring crystallization l=5

Monitoring crystallization l=6

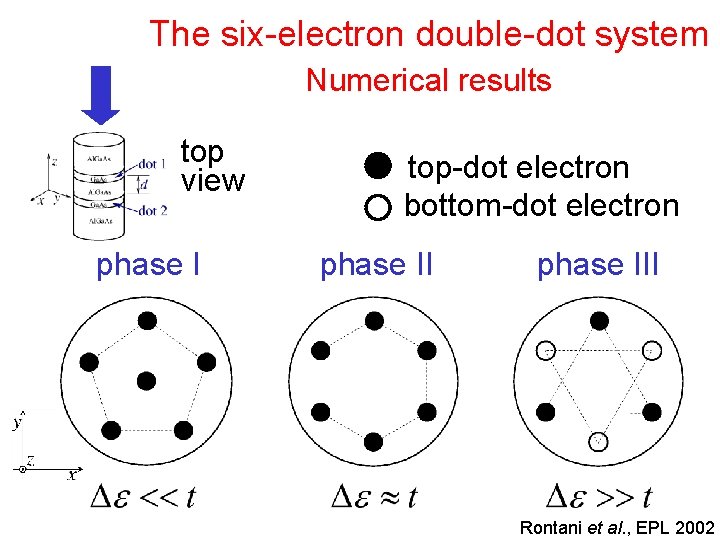
The six-electron double-dot system Numerical results top view phase I top-dot electron bottom-dot electron phase III Rontani et al. , EPL 2002

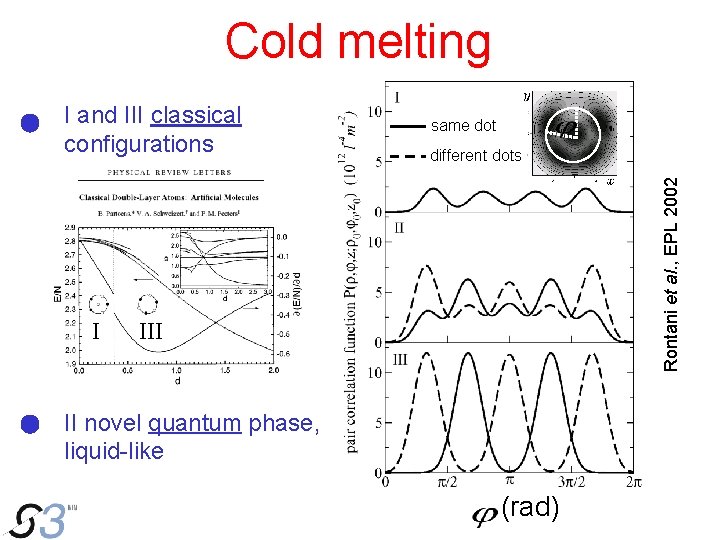
Cold melting I same dot different dots Rontani et al. , EPL 2002 I and III classical configurations III II novel quantum phase, liquid-like (rad)

Conclusion phase diagram of low-density quantum dots spin-unpolarized N = 6 ground state classically metastable phase close to melting How to measure? inelastic light scattering [EPL 58, 555 (2002); cond-mat/0506143] tunneling spectroscopies [cond-mat/0408454] FIRB, COFIN-2003, MAE, INFM I. T. Calcolo Parallelo http: //www. s 3. infm. it