Cold Gases Meet Condensed Matter Physics C Salomon

Cold Gases Meet Condensed Matter Physics C. Salomon Laboratoire Kastler Brossel, Ecole Normale Supérieure & UPMC, Paris, FR EMMI, GSI, Darmstadt, July 17 th, 2008

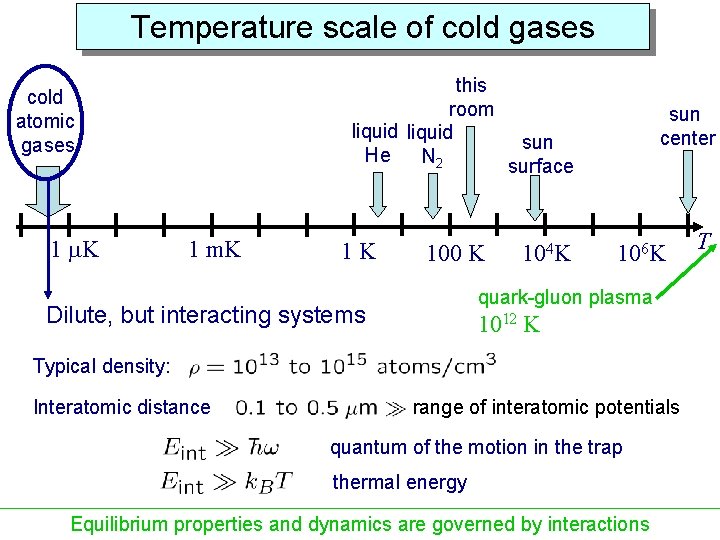
Temperature scale of cold gases this room liquid sun He N 2 surface cold atomic gases 1 m. K 1 K 100 K 104 K sun center 106 K quark-gluon plasma Dilute, but interacting systems 1012 K Typical density: Interatomic distance range of interatomic potentials quantum of the motion in the trap thermal energy Equilibrium properties and dynamics are governed by interactions T

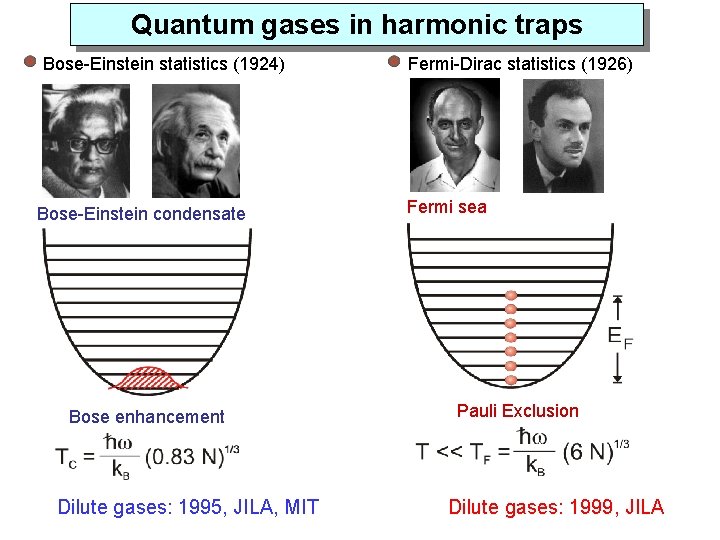
Quantum gases in harmonic traps Bose-Einstein statistics (1924) Bose-Einstein condensate Bose enhancement Dilute gases: 1995, JILA, MIT Fermi-Dirac statistics (1926) Fermi sea Pauli Exclusion Dilute gases: 1999, JILA

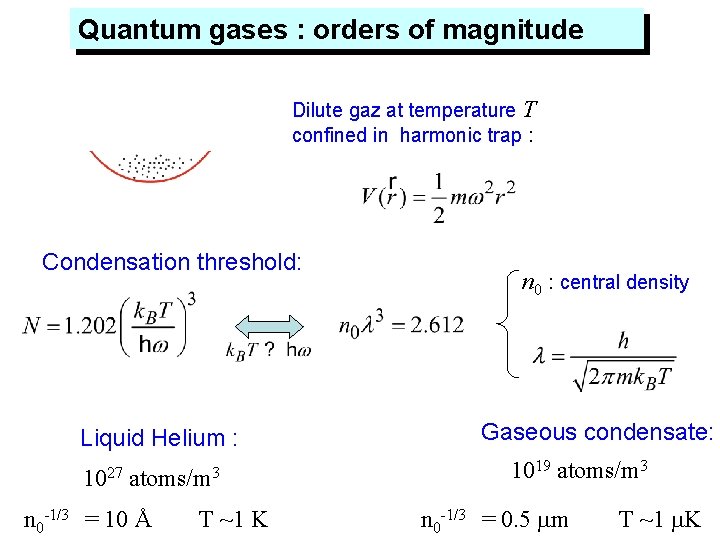
Quantum gases : orders of magnitude Dilute gaz at temperature T confined in harmonic trap : Condensation threshold: Liquid Helium : 1027 atoms/m 3 n 0 -1/3 = 10 Å T ~1 K n 0 : central density Gaseous condensate: 1019 atoms/m 3 n 0 -1/3 = 0. 5 mm T ~1 m. K

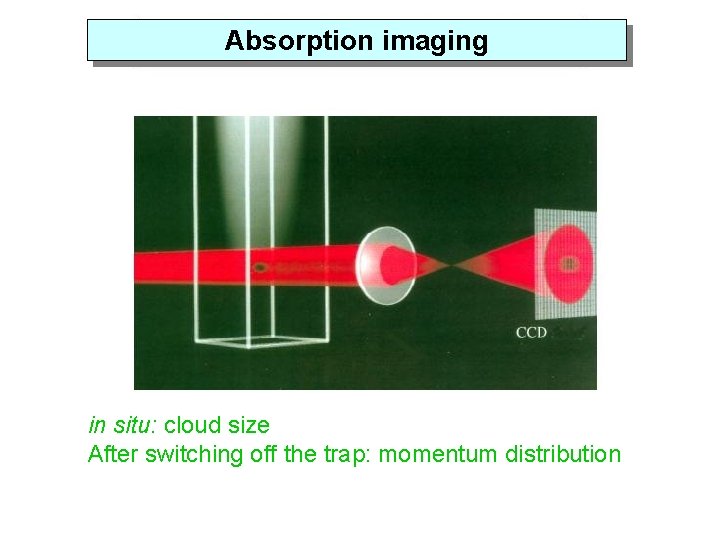
Absorption imaging in situ: cloud size After switching off the trap: momentum distribution

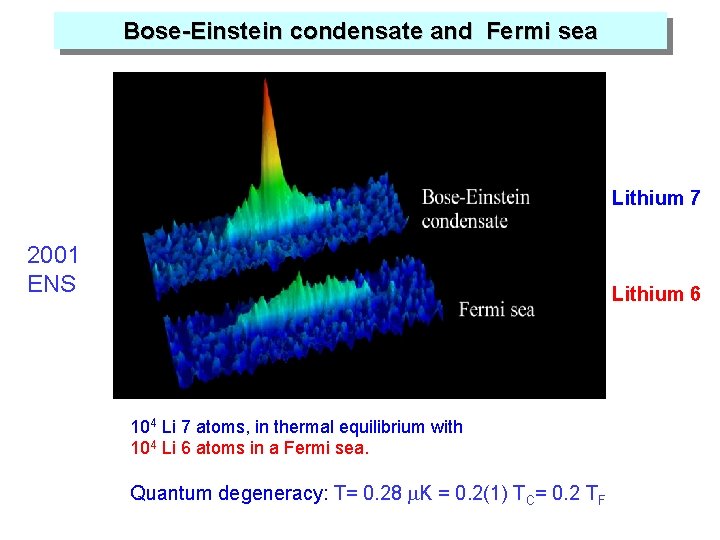
Bose-Einstein condensate and Fermi sea Lithium 7 2001 ENS Lithium 6 104 Li 7 atoms, in thermal equilibrium with 104 Li 6 atoms in a Fermi sea. Quantum degeneracy: T= 0. 28 m. K = 0. 2(1) TC= 0. 2 TF

Interest of cold gases Diluteness: atom-atom interactions described by 2 -body (and 3 body) physics At low energy: a single parameter, the scattering length Control of the sign and magnitude of interaction Control of trapping parameters: access to time dependent phenomena, out of equilibrium situations, 1 D, 2 D, 3 D Simplicity of detection n(k) Comparison with theory: 1 Gross-Pitaevskii, Bose and Fermi Hubbard models, 1 search for exotic phases, disorder effects, … Link with condensed matter (high Tc superconductors, magnetism in lattices), nuclear physics, high energy physics (quark-gluon plasma), and astrophysics (neutron stars) k/k. F 1 Towards quantum simulation with cold atoms « a la Feynman »

This talk 3 examples of the physics of strongly correlated systems Tuning atom-atom interactions: n(k) 1) Superfluidity in strongly interacting Fermi gas: a high Tc system n(k) 1 1 Tuning the trapping potential: 2) The Mott-Insulator transition in a 3 D periodic potential 3) Superfluidity in 2 D Bose gas: the Berezinski-Kosterlitz-Thouless transition 1 1 k/k. F

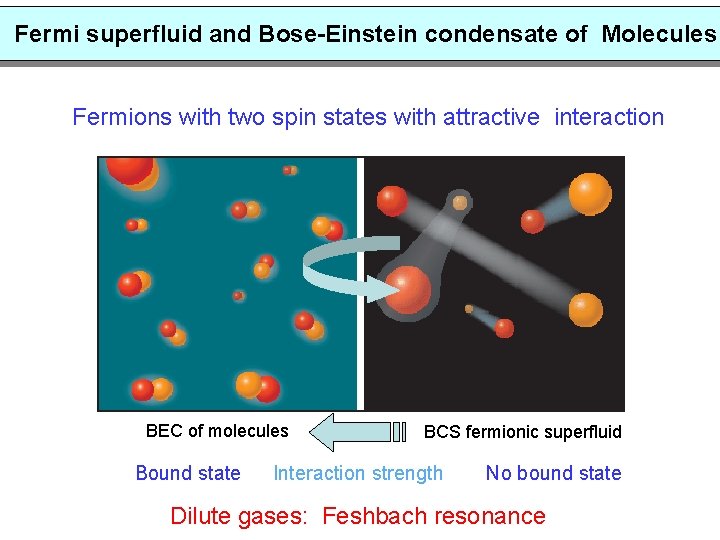
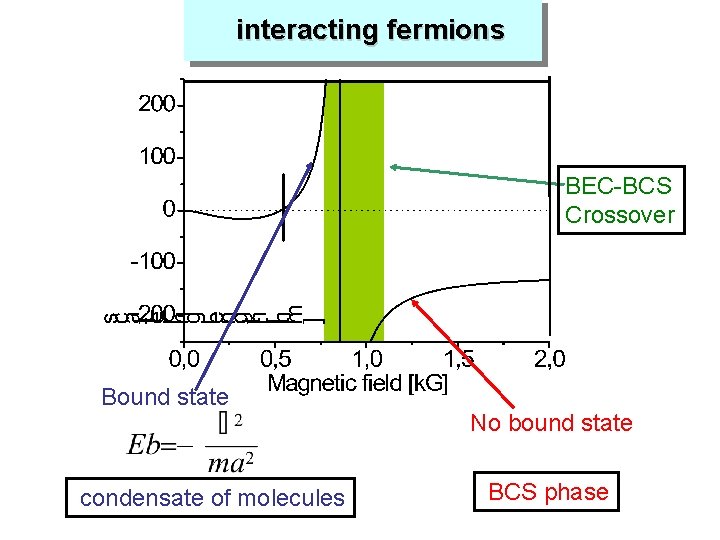
Fermi superfluid and Bose-Einstein condensate of Molecules Fermions with two spin states with attractive interaction BEC of molecules Bound state BCS fermionic superfluid Interaction strength No bound state Dilute gases: Feshbach resonance

n(k) 1 1 Tuning atom-atom interactions 1 1 k/k. F

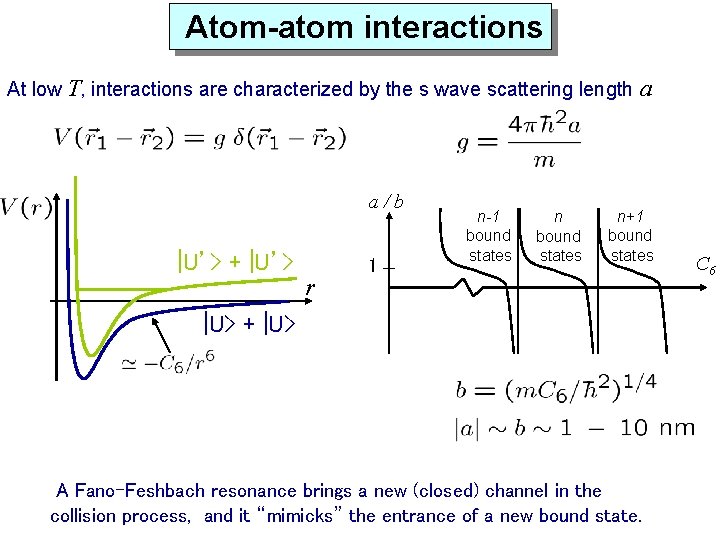
Atom-atom interactions At low T, interactions are characterized by the s wave scattering length a/b |U’> + |U’> r 1 n-1 bound states n bound states a n+1 bound states |U> + |U> A Fano-Feshbach resonance brings a new (closed) channel in the collision process, and it “mimicks” the entrance of a new bound state. C 6

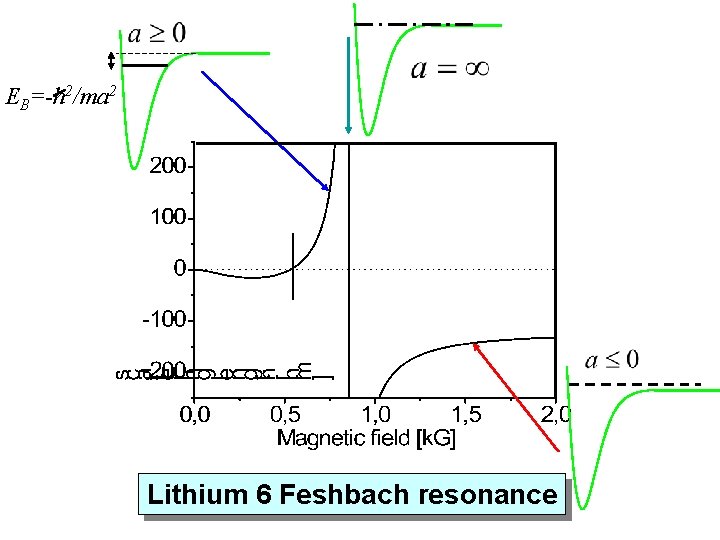
EB=-h 2/ma 2 Lithium 6 Feshbach resonance

interacting fermions BEC-BCS Crossover Bound state condensate of molecules No bound state BCS phase

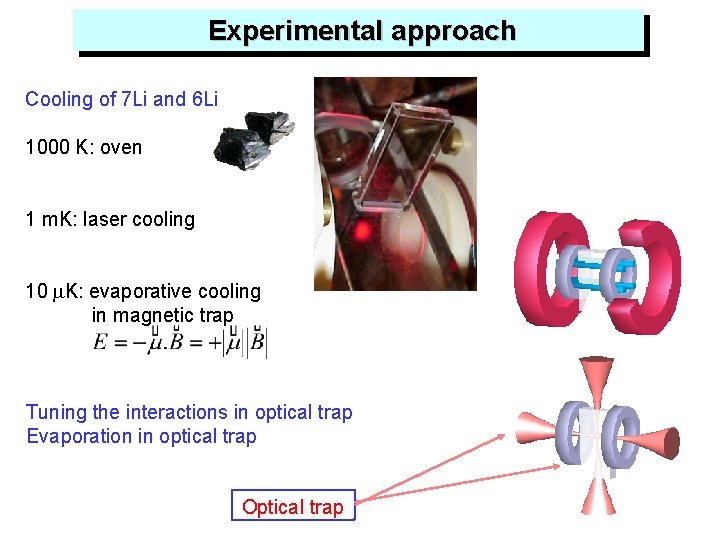
Experimental approach Cooling of 7 Li and 6 Li 1000 K: oven 1 m. K: laser cooling 10 m. K: evaporative cooling in magnetic trap Tuning the interactions in optical trap Evaporation in optical trap Optical trap

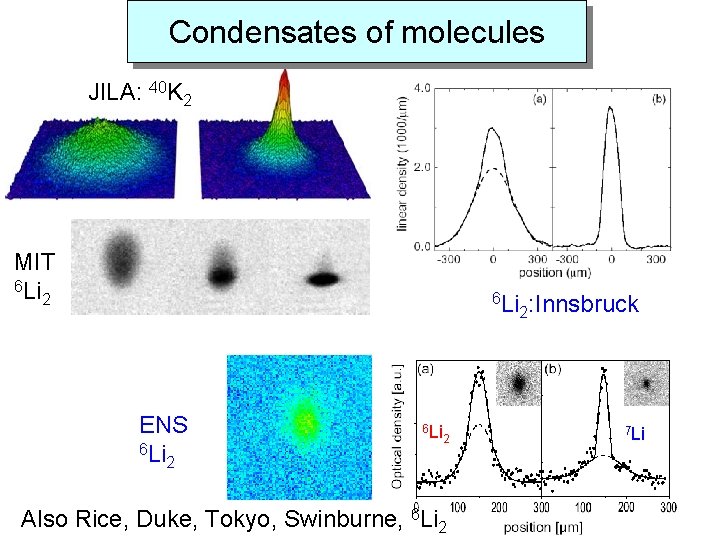
Condensates of molecules JILA: 40 K 2 MIT 6 Li 2 6 Li ENS 6 Li 2 Also Rice, Duke, Tokyo, Swinburne, 6 Li 2 2: Innsbruck 7 Li

Experiments on BEC-BCS crossover Interaction between molecules and lifetime of molecules Unitarity regime: k. Fa>>1 ? Probing fermionic superfluidity Momentum distribution of particles Superfluidity with imbalanced Fermi spheres Can we measure the excitation gap ? A high temperature superfluid: Tc=0. 2 TF JILA, Innsbruck, MIT, ENS, Rice, Duke, Swinburne, Tokyo, …

Universal equation of state of the unitary Fermi gas Balanced Fermi gas ( ) x numerical factor First example of a quantum simulator ! Determination of x Theory BCS 0. 59 Astrakharchik Experiment ENS (6 Li) 0. 42(15) 0. 42(1) Rice (6 Li) 0. 46(5) Perali 0. 455 JILA(40 K) 0. 46(10) Carlson 0. 42(1) Innsbruck (6 Li) 0. 27(10) Haussmann 0. 36 Duke (6 Li) 0. 51(4)

Direct proof of superfluidity: classical vs. quantum rotation Rotating classical gas velocity field of a rigid body Rotating a quantum macroscopic object macroscopic wave function: In a place where , irrotational velocity field: The only possibility to generate a non-trivial rotating motion is to nucleate quantized vortices (points in 2 D or lines in 3 D) Feynman, Onsager Vortices now all have the same sign, imposed by the external rotation

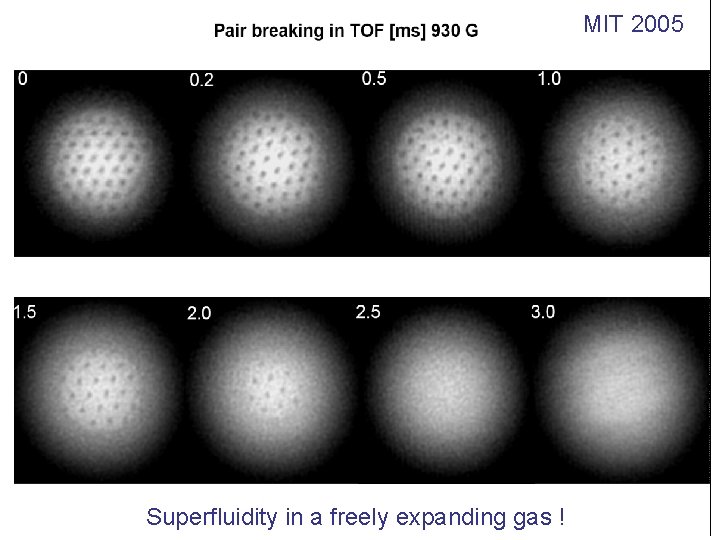
MIT 2005: Vortex lattices in the BEC-BCS Crossover Energy [MHz] Direct proof of superfluidity BEC side BCS side M. Zwierlein A. . Schirotzek C. Stan C. Schunk P. Zarth W. Ketterle Science 05 Magnetic Field [G]

MIT 2005 Superfluidity in a freely expanding gas !

2: Creating artificial crystals

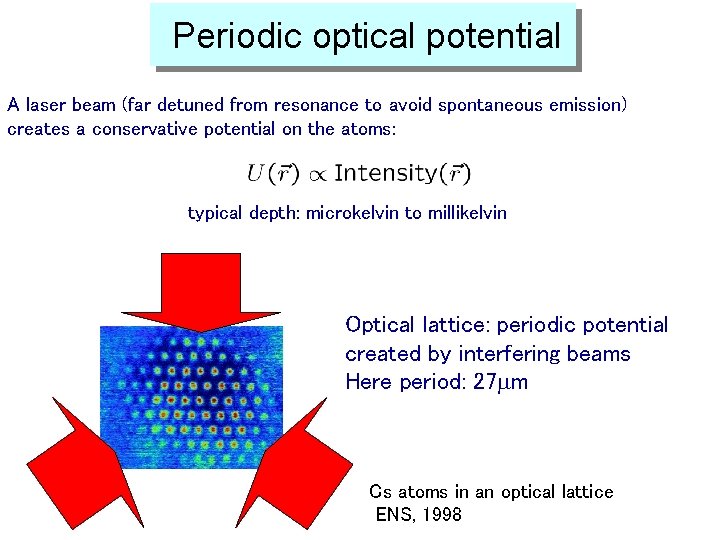
Periodic optical potential A laser beam (far detuned from resonance to avoid spontaneous emission) creates a conservative potential on the atoms: typical depth: microkelvin to millikelvin Optical lattice: periodic potential created by interfering beams Here period: 27 mm Cs atoms in an optical lattice ENS, 1998

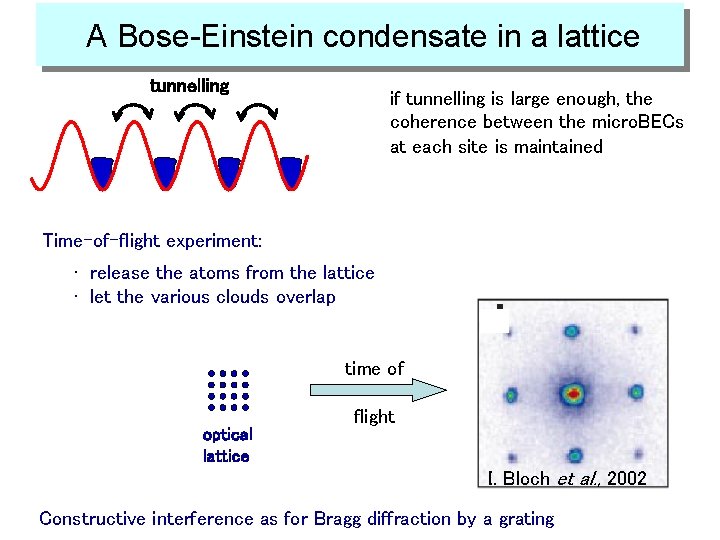
A Bose-Einstein condensate in a lattice tunnelling if tunnelling is large enough, the coherence between the micro. BECs at each site is maintained Time-of-flight experiment: • release the atoms from the lattice • let the various clouds overlap time of optical lattice flight I. Bloch et al. , 2002 Constructive interference as for Bragg diffraction by a grating

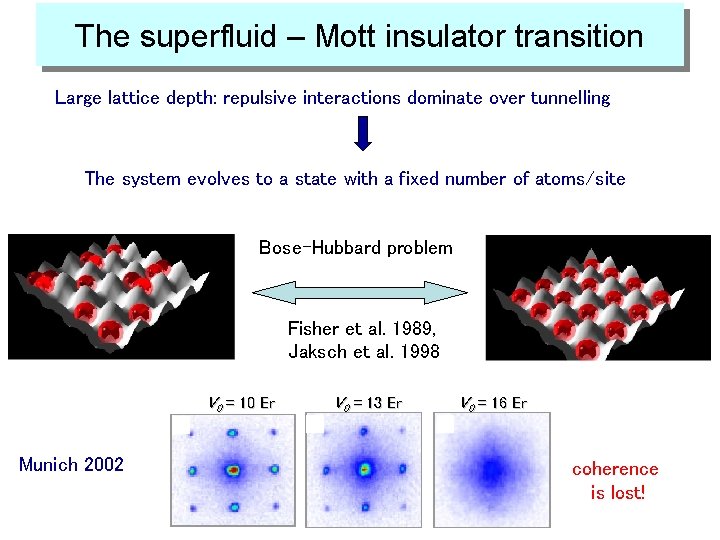
The superfluid – Mott insulator transition Large lattice depth: repulsive interactions dominate over tunnelling The system evolves to a state with a fixed number of atoms/site Bose-Hubbard problem Fisher et al. 1989, Jaksch et al. 1998 V 0 = 10 Er Munich 2002 V 0 = 13 Er V 0 = 16 Er coherence is lost!

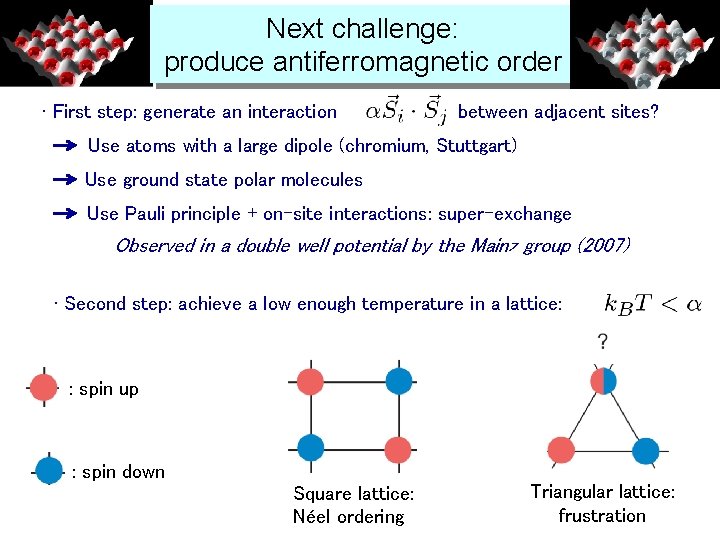
Next challenge: produce antiferromagnetic order • First step: generate an interaction between adjacent sites? Use atoms with a large dipole (chromium, Stuttgart) Use ground state polar molecules Use Pauli principle + on-site interactions: super-exchange Observed in a double well potential by the Mainz group (2007) • Second step: achieve a low enough temperature in a lattice: : spin up : spin down Square lattice: Néel ordering Triangular lattice: frustration

3: Cold gases in low dimensions

Two-dimensional Quantum Physics Quantum wells and MOS structures High Tc superconductivity also Quantum Hall effect, films of superfluid helium, … Key words of two-dimensional physics: • absence of true long range order (no BEC stricto sensu) • existence of a new kind of phase transition (Kosterlitz-Thouless) • No spin-statistics theorem, and existence of parastatistics: any-ons • Non abelian physics: towards topological quantum computing ? ?

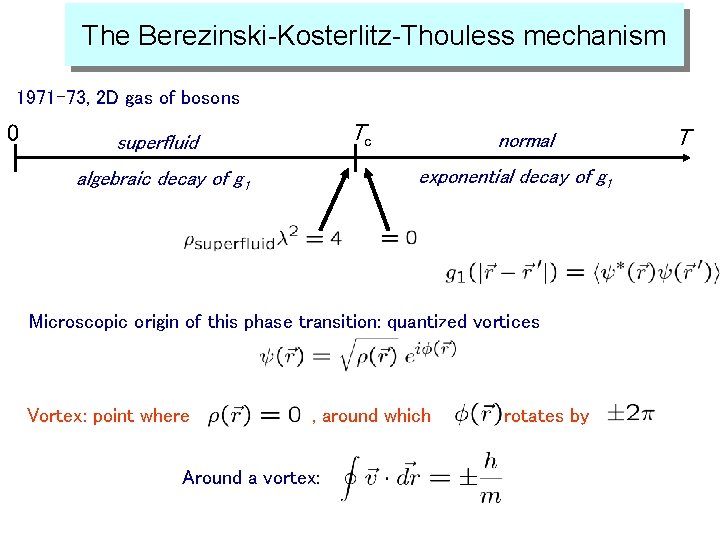
The Berezinski-Kosterlitz-Thouless mechanism 1971 -73, 2 D gas of bosons 0 Tc superfluid normal exponential decay of g 1 algebraic decay of g 1 Microscopic origin of this phase transition: quantized vortices Vortex: point where , around which Around a vortex: rotates by T

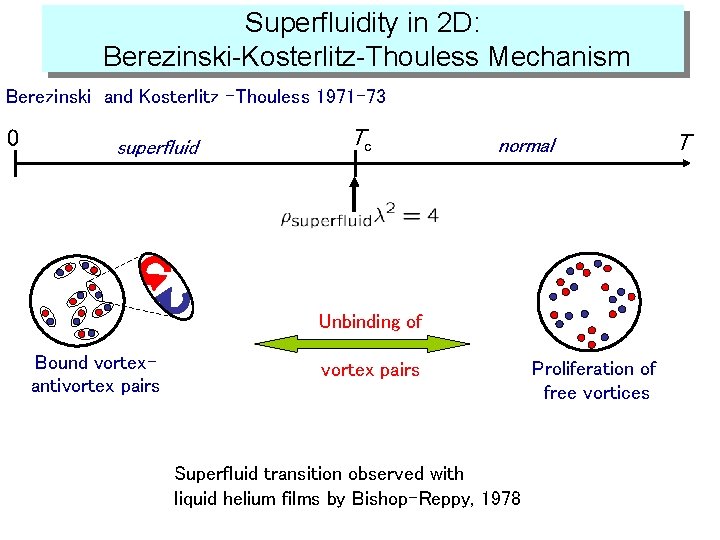
in 22 D: However: Superfluidity in dimensions Berezinski-Kosterlitz-Thouless Mechanism Berezinski and Kosterlitz –Thouless 1971 -73 0 superfluid Tc normal Unbinding of Bound vortexantivortex pairs Superfluid transition observed with liquid helium films by Bishop-Reppy, 1978 Proliferation of free vortices T

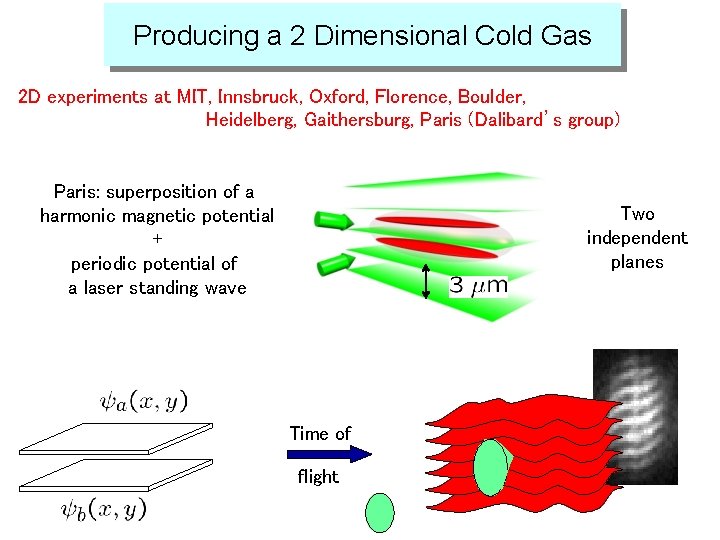
Producing a cold 2 D gas Producing a 2 Dimensional Cold Gas 2 D experiments at MIT, Innsbruck, Oxford, Florence, Boulder, Heidelberg, Gaithersburg, Paris (Dalibard’s group) Paris: superposition of a harmonic magnetic potential + periodic potential of a laser standing wave Two independent planes Time of flight

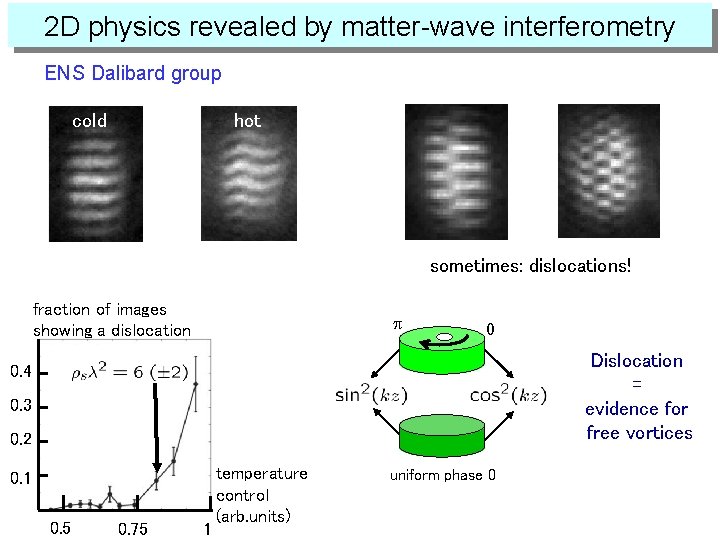
2 D physics revealed by matter-wave interferometry ENS Dalibard group cold hot sometimes: dislocations! fraction of images showing a dislocation p 0 Dislocation = evidence for free vortices 0. 4 0. 3 0. 2 0. 1 0. 5 0. 75 1 temperature control (arb. units) uniform phase 0

Prospects With cold atoms, one can simulate several many-body Hamiltonians • Bosons, fermions, and mixtures • Pairing with mismatched Fermi spheres, exotic phases • Periodic potential or disordered (Anderson localization) • Gauge field with rotation or geometrical phase • Non abelian Gauge field for simulating the Hamiltonian of strong interactions in particle physics • Quantum Hall physics and Laughlin states New experimental methods: • Image a many-body wavefunction with micrometer resolution • Measure correlation functions • Photoemission spectroscopy to measure Fermi surface and single particle excitations • Time-dependent phenomena in 1, 2, and 3 D

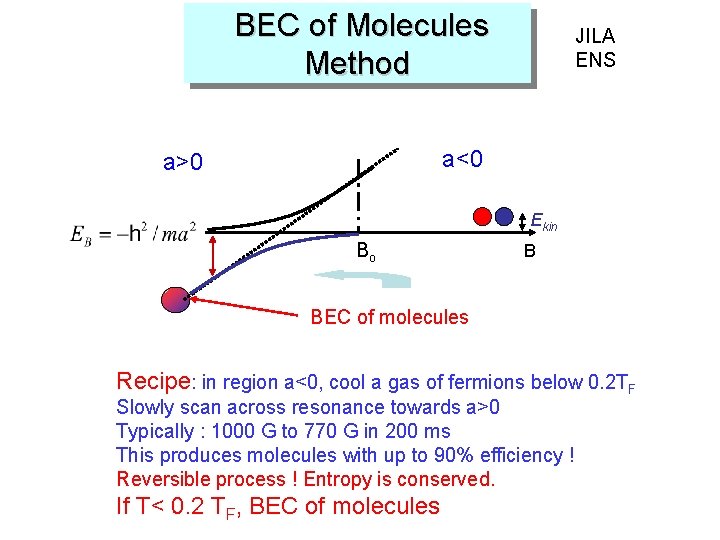
BEC of Molecules Method JILA ENS a<0 a>0 Ekin Bo B BEC of molecules Recipe: in region a<0, cool a gas of fermions below 0. 2 TF Slowly scan across resonance towards a>0 Typically : 1000 G to 770 G in 200 ms This produces molecules with up to 90% efficiency ! Reversible process ! Entropy is conserved. If T< 0. 2 TF, BEC of molecules