Coherent Quantum Phase Slip Oleg Astafiev NEC Smart

Coherent Quantum Phase Slip Oleg Astafiev NEC Smart Energy Research Laboratories, Japan and The Institute of Physical and Chemical Research (RIKEN), Japan Coherent quantum phase slip, Nature, 484, 355 (2012) RIKEN/NEC: O. V. Astafiev, S. Kafanov, Yu. A. Pashkin, J. S. Tsai Rutgers: L. B. Ioffe Jyväskylä: K. Yu. Arutyunov Weizmann: D. Shahar, O. Cohen

Outline Ø Introduction. Phase slip (PS) and coherent quantum phase slip (CQPS) Ø Duality between CQPS and the Josephson Effect Ø CQPS qubits Ø Superconductor-insulator transition (SIT) materials Ø Experimental demonstration of CQPS

Coherent Quantum Phase Slips (CQPS) Ø Very fundamental phenomenon of superconductivity (as fundamental as the Josephson Effect) Ø Exactly dual to the Josephson Effect • Flux interference (SQUID) Charge interference • Charge tunneling Flux tunneling Applications Ø Quantum information • Qubits without Josephson junctions Ø Metrology • Current standards (dual to voltage standards)

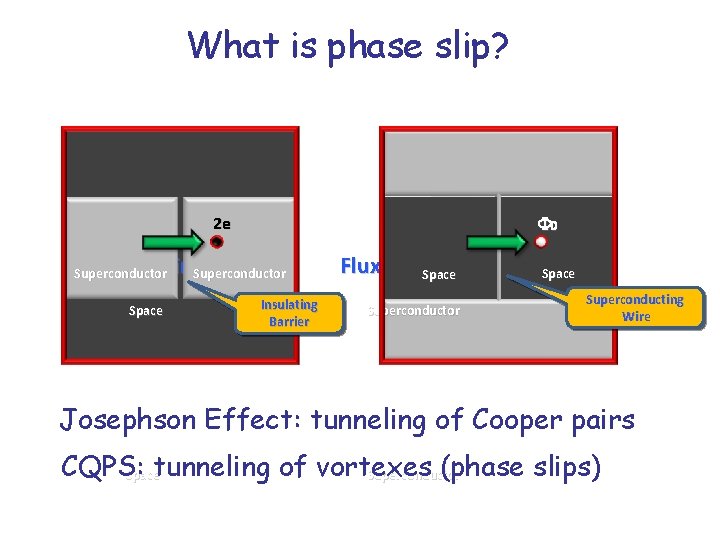
What is phase slip? F 0 2 e Cooper pair Superconductor tunneling Superconductor Space Insulating Barrier Flux tunneling Space Superconductor Space Superconducting Wire Josephson Effect: tunneling of Cooper pairs CQPS: (phase slips) Spacetunneling of vortexes Superconductor

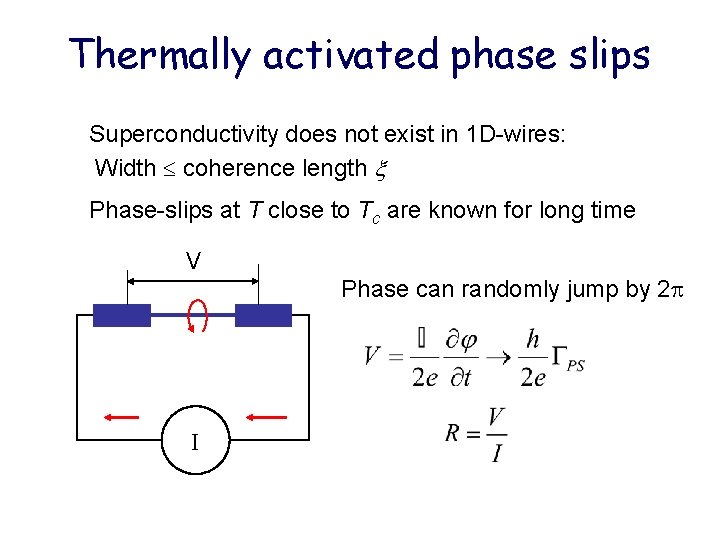
Thermally activated phase slips Superconductivity does not exist in 1 D-wires: Width coherence length Phase-slips at T close to Tc are known for long time V Phase can randomly jump by 2 I

Thermally activated and Quantum phase slip Thermally activated phase slips Are phase slips possible at T = 0? V Signature of QPS? Quantum phase slip T k. T At T = 0: Phase slips due to quantum fluctuations(? )

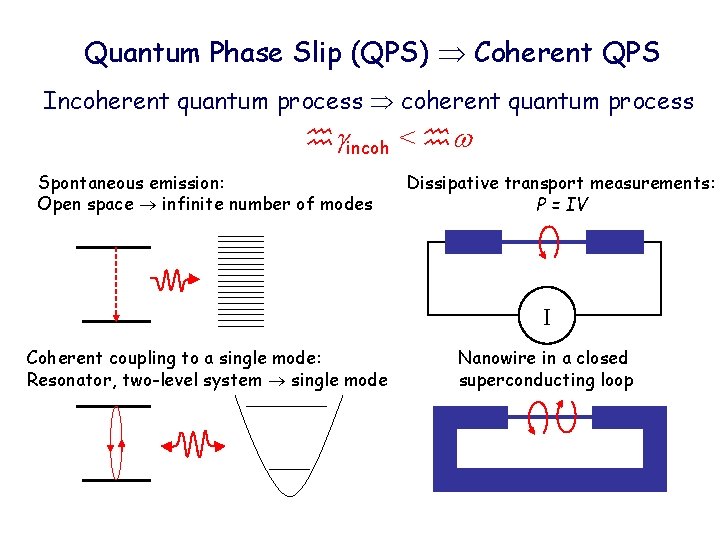
Quantum Phase Slip (QPS) Coherent QPS Incoherent quantum process incoh < Spontaneous emission: Open space infinite number of modes Dissipative transport measurements: P = IV I Coherent coupling to a single mode: Resonator, two-level system single mode Nanowire in a closed superconducting loop

Duality between CQPS and the Josephson Effect Mooij, Nazarov. Nature Physics 2, 169 -172 (2006) Josephson junction Z Y Phase-slip junction L C 0 2 e The CQPS is completely dual to the Josephson effect

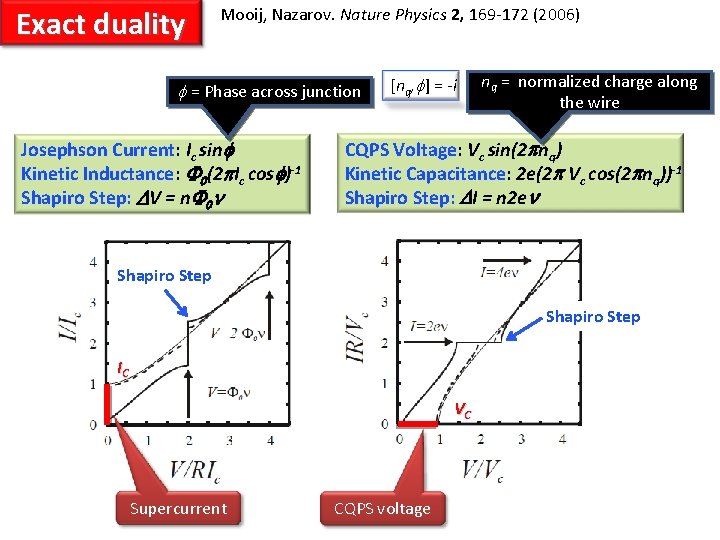
Exact duality Mooij, Nazarov. Nature Physics 2, 169 -172 (2006) f = Phase across junction Josephson Current: Ic sinf Kinetic Inductance: F 0(2 p. Ic cosf)-1 Shapiro Step: DV = n. F 0 n [nq, f] = -i nq = normalized charge along the wire CQPS Voltage: Vc sin(2 pnq) Kinetic Capacitance: 2 e(2 p Vc cos(2 pnq))-1 Shapiro Step: DI = n 2 en Shapiro Step IC VC Supercurrent CQPS voltage

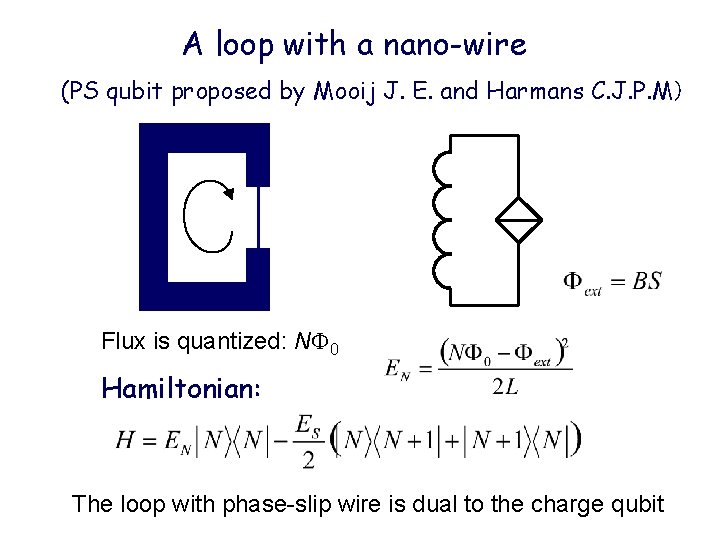
A loop with a nano-wire (PS qubit proposed by Mooij J. E. and Harmans C. J. P. M） Flux is quantized: N 0 Hamiltonian: The loop with phase-slip wire is dual to the charge qubit

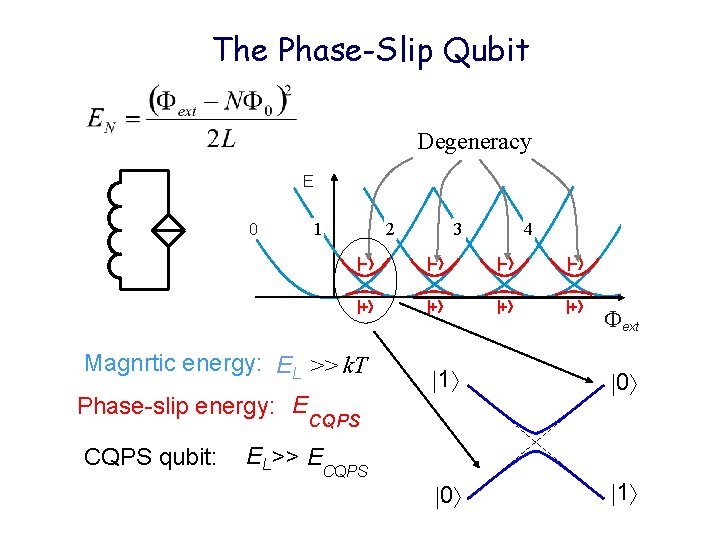
The Phase-Slip Qubit Degeneracy E 0 1 2 CQPS qubit: 4 - - + + Magnrtic energy: EL >> k. T Phase-slip energy: E 3 ext 1 0 0 1 CQPS EL >> E CQPS

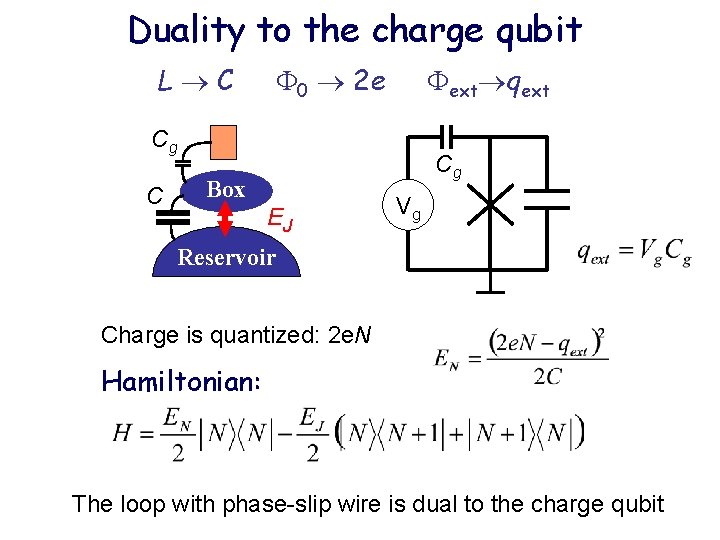
Duality to the charge qubit L C 0 2 e ext qext Cg C Cg Box EJ Vg Reservoir Charge is quantized: 2 e. N Hamiltonian: The loop with phase-slip wire is dual to the charge qubit

Choice of materials Ø Loops of usual (BCS) superconductors (Al, Ti) did not show qubit behavior Ø BCS superconductors become normal metals, when superconductivity is suppressed Ø Special class of superconductors turn to insulators, when superconductivity is suppressed Ø Superconductor-insulator transition (SIT) Ø High resistive films in normal state high kinetic inductance

Superconductor-insulator transition (SIT) 107 Requirements: high sheet resistance > 1 k Sheet resistance R□ ( ) 106 In. Ox, Ti. N, Nb. N 105 High resistance high kinetic inductance 104 103 102 101 0 5 10 T (K) 15 The materials demonstrating SIT transition are the most promising for CQPS

The device N 0 Amorphous In. Ox film: R□ = 1. 7 k (N+1) 0 E Es (N+1/2) 0 ext MW in Gold ground-planes In. Ox 0. 5 mm In. Ox Step-impedance resonator: High kinetic inductance 40 nm 5 m MW out

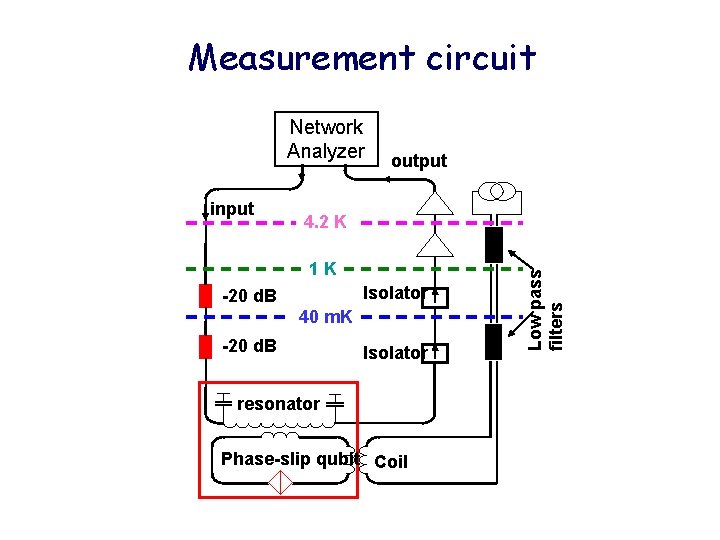
Measurement circuit Network Analyzer 4. 2 K 1 K Isolator -20 d. B 40 m. K -20 d. B Isolator resonator Phase-slip qubit Coil Low pass filters input output

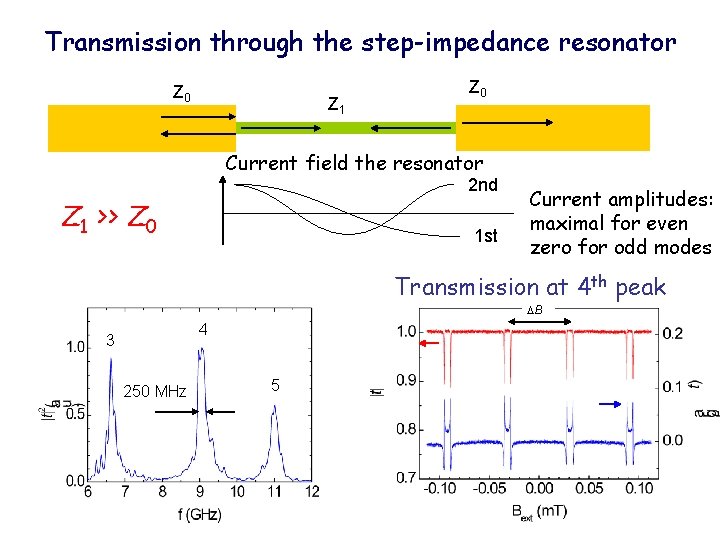
Transmission through the step-impedance resonator Z 0 Z 1 Z 0 Current field the resonator 2 nd Z 1 >> Z 0 1 st Current amplitudes: maximal for even zero for odd modes Transmission at 4 th peak B 4 3 250 MHz 5

Two-tone spectroscopy We measure transmission through the resonator at fixed frequency fres Another frequency fprobe is swept 0 arg(t) (mrad) f = 260 MHz -5 The fitting curve: Ip = 24 n. A, ES/h = 4. 9 GHz

Current driven loop with CQPS Ip |1 M |0 I 0 RWA: Transitions can happen only when ES 0 ES

The result is well reproducible Three identical samples show similar behavior with energies 4. 9, 5. 8 and 9. 5 GHz After “annealing” at room temperature In. Ox becomes more superconducting. The samples were loaded three times with intervals about 1 months. Es is decreased with time.

Wide range spectroscopy 2 fprobe + fres (3 -photons) fprobe + fres (2 photons) E / h = (2 I d ) + E 2 = p h 2 s fprobe Linear inductance!

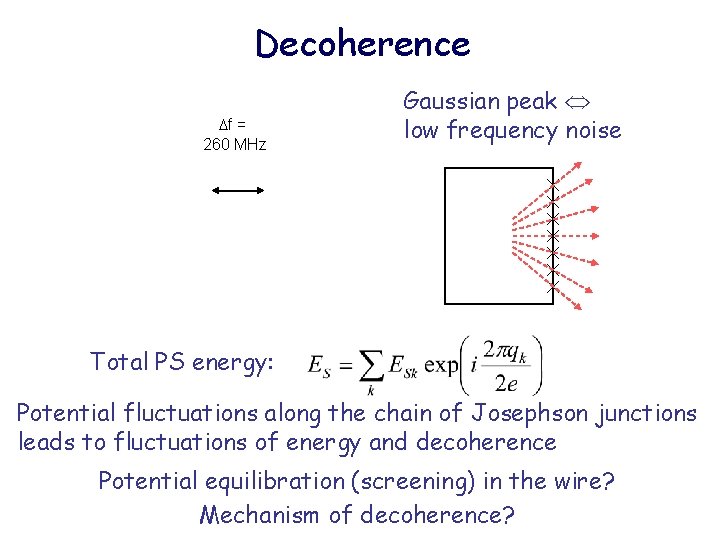
Decoherence f = 260 MHz Gaussian peak low frequency noise Total PS energy: Potential fluctuations along the chain of Josephson junctions leads to fluctuations of energy and decoherence Potential equilibration (screening) in the wire? Mechanism of decoherence?

Nb. N thin films R� 2 k In MW measurements Tc 5 K L 1. 6 n. H/sq 20 different loops with wires of 20 -50 nm width Many qubits can be identified General tendency: the higher resistance, the higher ES

Transmission amplitude f (GHz) Nb. N qubits

Conclusion Ø We have experimentally demonstrated Coherent Quantum Phase Slip Ø Phase-slip qubit has been realized in thin highly resistive films of In. Ox and Nb. N Ø Mechanism of decoherence in nano-wires is an open question