Coherent Multiscale Image Processing using Quaternion Wavelets Wai

Coherent Multiscale Image Processing using Quaternion Wavelets Wai Lam Chan M. S. defense Committee: Hyeokho Choi, Richard Baraniuk, Michael Orchard

Image Location Information Edges: “location” “orientation” Goal: Encode/Estimate location information from phase (coherent processing)

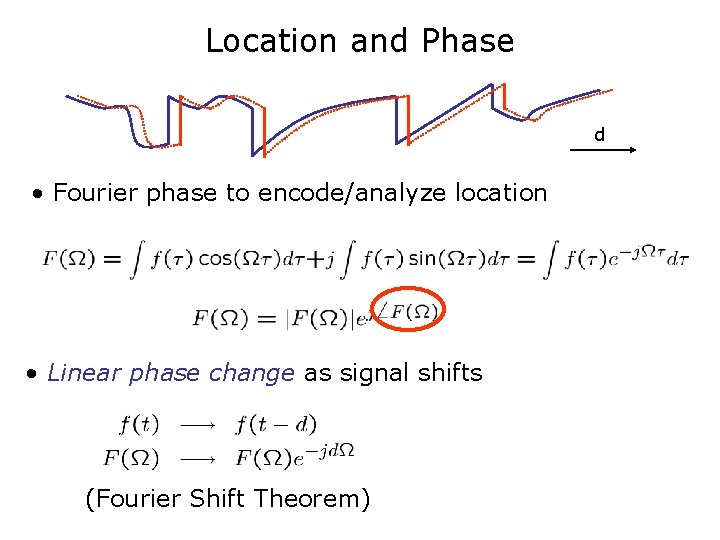
Location and Phase d • Fourier phase to encode/analyze location • Linear phase change as signal shifts (Fourier Shift Theorem)

Image Geometry and Phase Rich’s picture Rich’s phase-only picture • Global phase (no localization) Rich’s phase + Cameraman’s amplitude

Local Fourier Analysis • Local Fourier analysis for “location” • Short time Fourier transform (Gabor analysis) • Local Fourier phase (relates to local geometry)

Wavelet Analysis 1. “Multiscale” analysis 2. Sparse representation of piecewise smooth signals 3. Orthonormal basis / tight frame 4. Fast computation by filter banks But conventional discrete wavelets are “Real” Lack of phase to encode geometry!

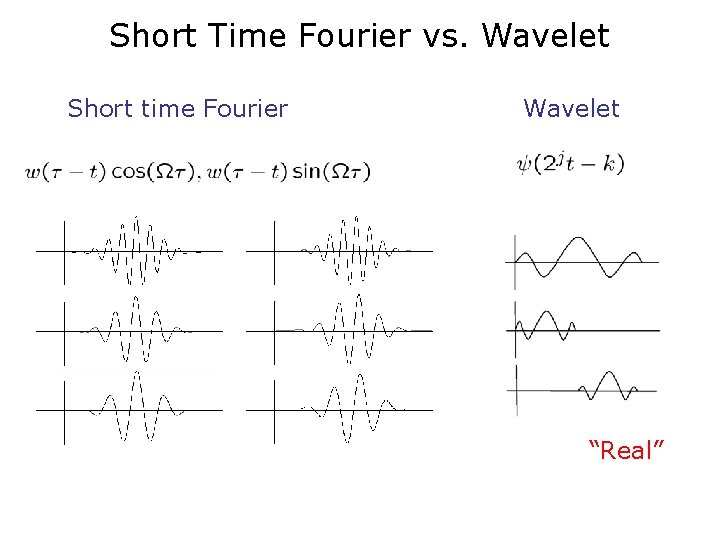
Short Time Fourier vs. Wavelet Short time Fourier Wavelet “Real”

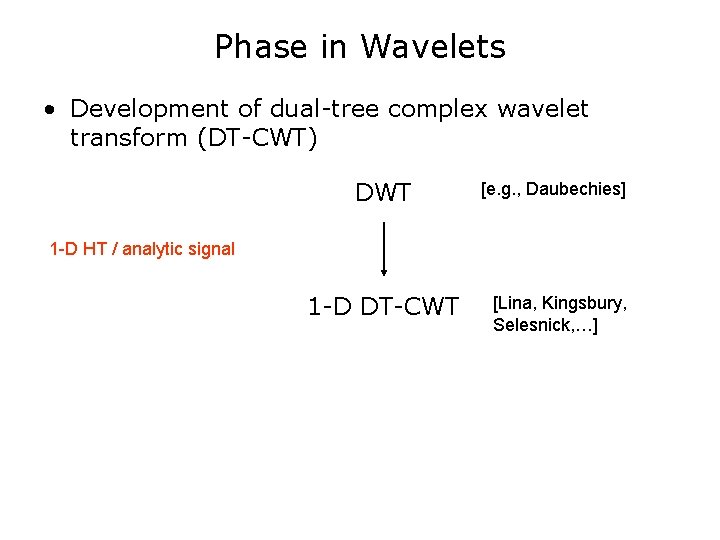
Phase in Wavelets • Development of dual-tree complex wavelet transform (DT-CWT) DWT [e. g. , Daubechies] 1 -D HT / analytic signal 1 -D DT-CWT [Lina, Kingsbury, Selesnick, …]

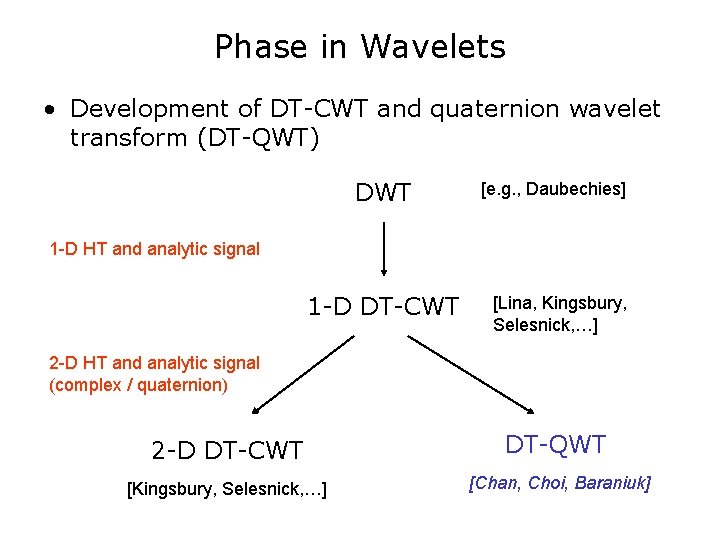
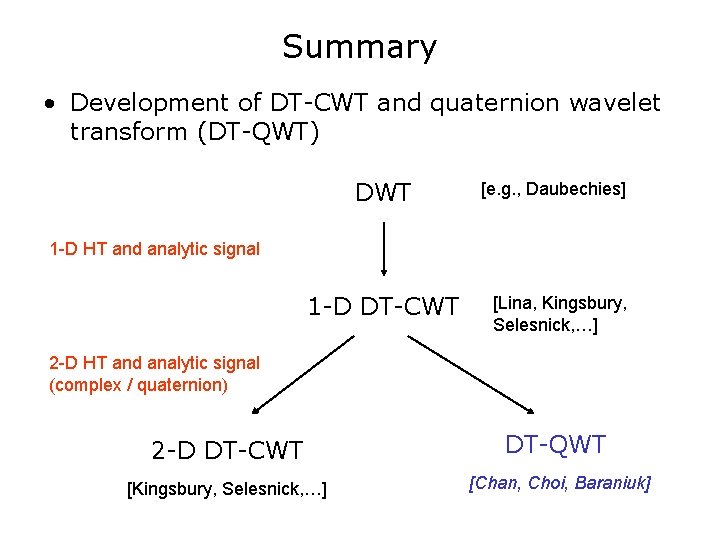
Phase in Wavelets • Development of DT-CWT and quaternion wavelet transform (DT-QWT) DWT [e. g. , Daubechies] 1 -D HT and analytic signal 1 -D DT-CWT [Lina, Kingsbury, Selesnick, …] 2 -D HT and analytic signal (complex / quaternion) 2 -D DT-CWT DT-QWT [Kingsbury, Selesnick, …] [Chan, Choi, Baraniuk]

Major Thesis Contributions • QWT Construction • QWT Properties • Magnitude-phase representation • Shift Theorem • QWT Applications • Edge Estimation • Image Flow Estimation

Phase for Wavelets ? • Need to have quadrature component • phase shift of

Complex Wavelet • Complex wavelet transform (CWT) [Kingsbury, Selesnick, Lina]

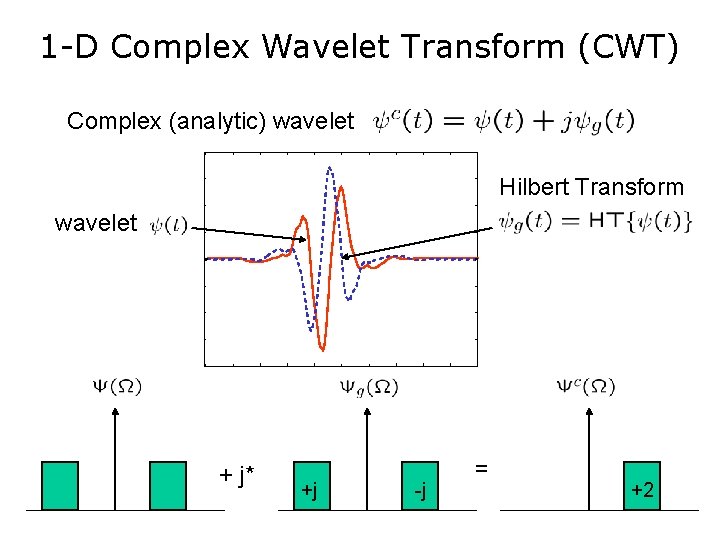
1 -D Complex Wavelet Transform (CWT) Complex (analytic) wavelet Hilbert Transform wavelet + j* +j -j = +2

2 -D Complex Fourier Transform (CFT) • Phase ambiguity • cannot obtain from phase shift

Quaternion Fourier Transform (QFT) [Bülow et al. ] • Separate 4 quadrature components • Organize as quaternion • Quaternions: • Multiplication rules: and

QFT Phase • Quaternion phase angles: Shift theorem • • QFT shift theorem: 1. invariant to signal shift 2. linear to signal shift encodes mixing of signal orientations

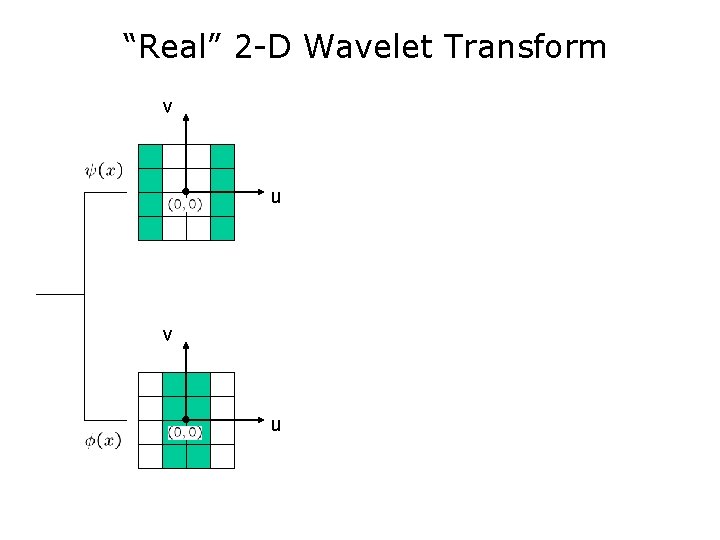
“Real” 2 -D Wavelet Transform v u

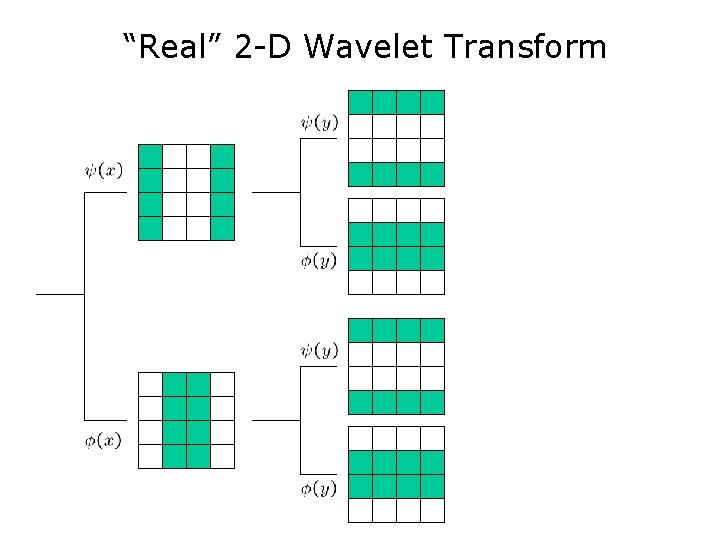
“Real” 2 -D Wavelet Transform

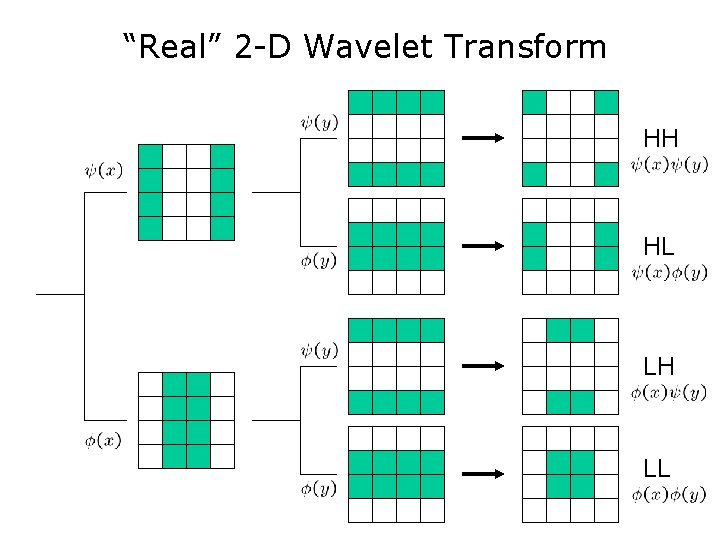
“Real” 2 -D Wavelet Transform HH HL LH LL

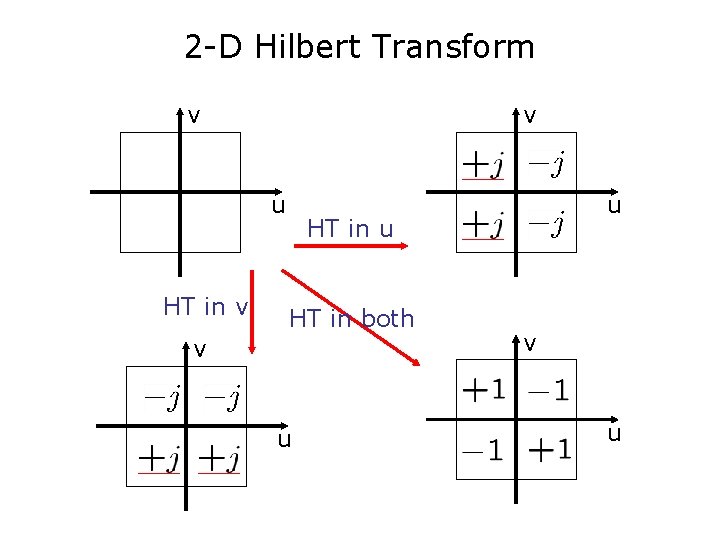
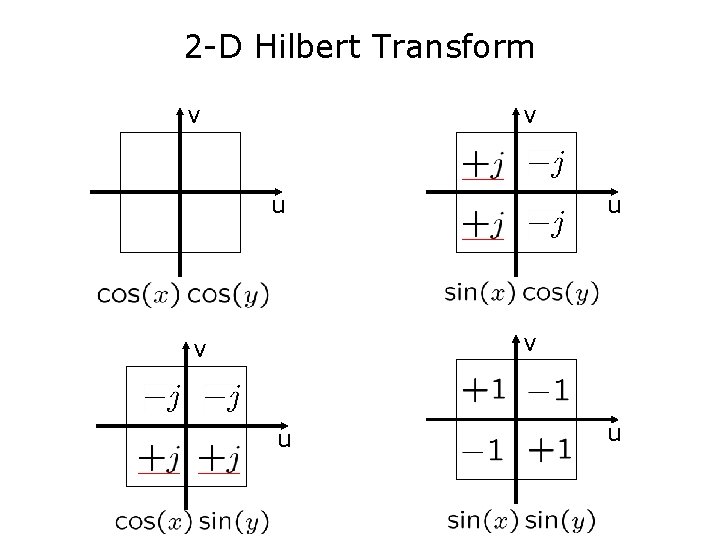
2 -D Hilbert Transform v v u HT in both v u

2 -D Hilbert Transform v v u u

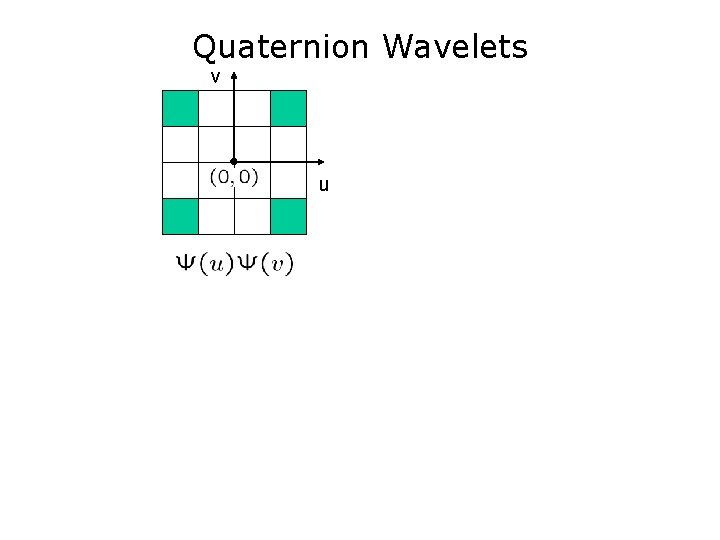
Quaternion Wavelets v u

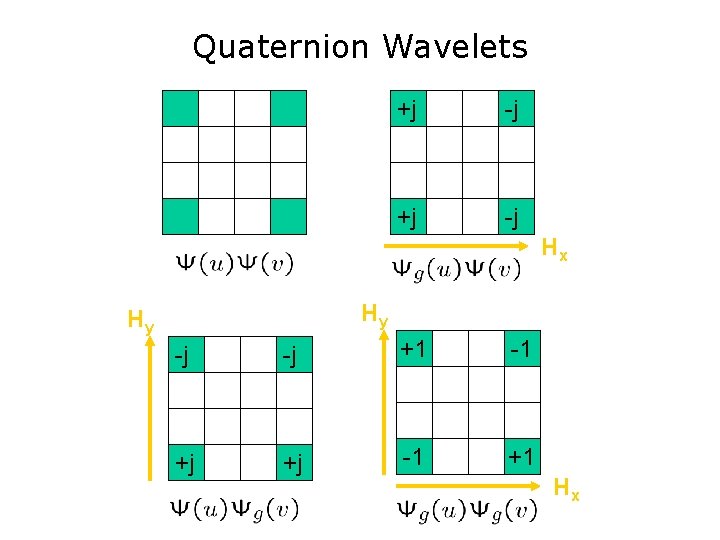
Quaternion Wavelets +j -j Hx Hy Hy -j -j +1 -1 +j +j -1 +1 Hx

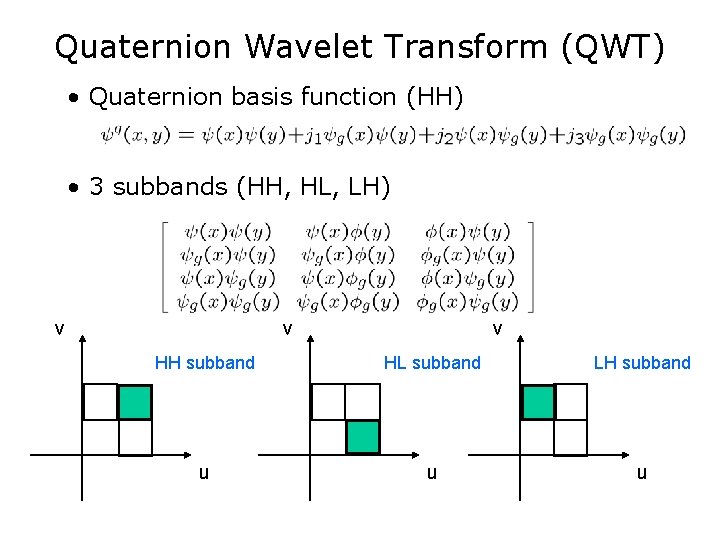
Quaternion Wavelet Transform (QWT) • Quaternion basis function (HH) • 3 subbands (HH, HL, LH) v v v HH subband HL subband LH subband u u u

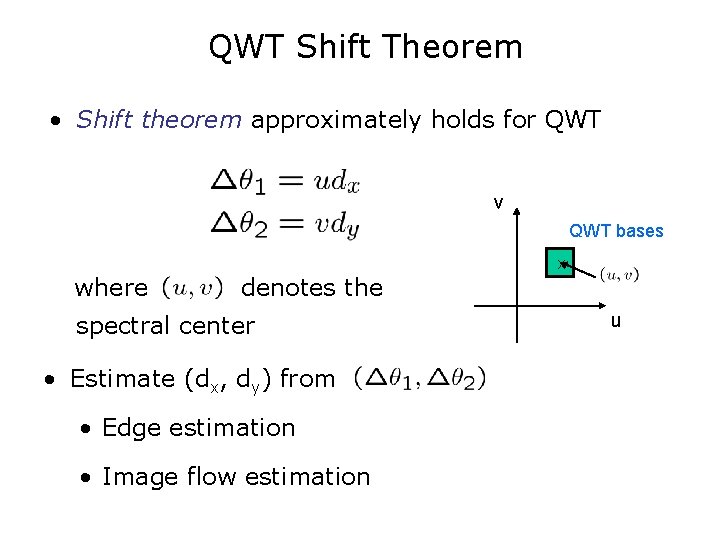
QWT Shift Theorem • Shift theorem approximately holds for QWT v QWT bases where denotes the spectral center • Estimate (dx, dy) from • Edge estimation • Image flow estimation x u

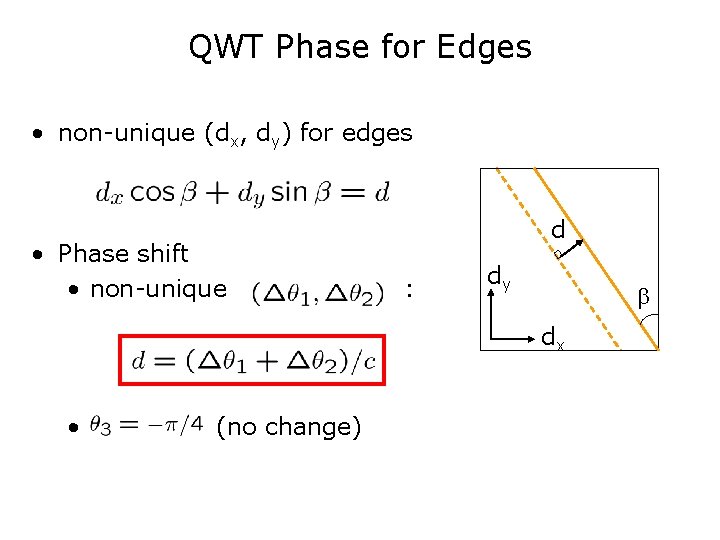
QWT Phase for Edges • non-unique (dx, dy) for edges • Phase shift • non-unique d : dy dx • (no change)

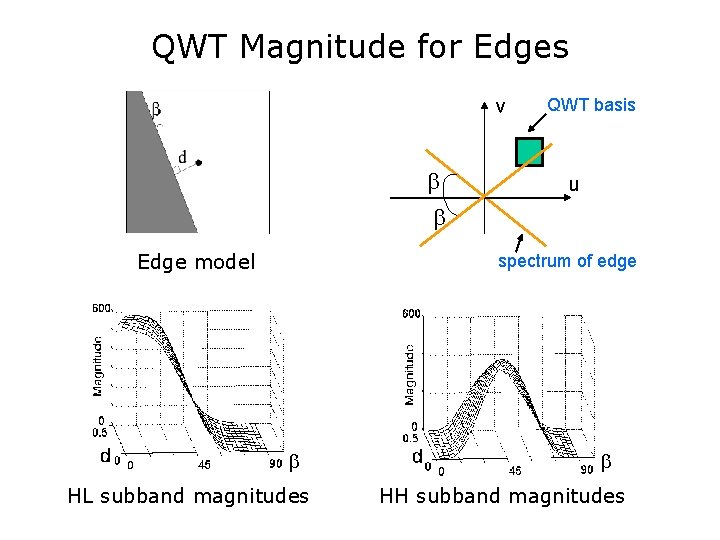
QWT Magnitude for Edges v Edge model QWT basis u spectrum of edge HL subband magnitudes HH subband magnitudes

QWT Edge Estimation • Edge parameter (offset/orientation) estimation – edge offset – QWT magnitude edge orientation

Multiscale Image Flow Estimation • Disparity estimation in QWT domain 1. QWT Shift Theorem 2. Multiscale phase-wrap correction 3. Efficient computation (O(N))

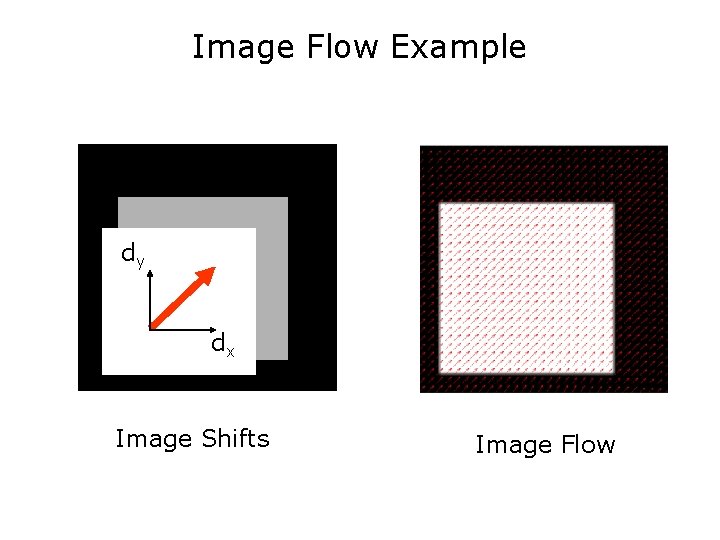
Image Flow Example dy dx Image Shifts Image Flow

Multiscale Estimation Algorithm • Step 1: Estimate from change in QWT phase for each image block • Step 2: Estimate (dx, dy) for each scale • Bilinear Interpolation • Multiscale phase unwrapping algorithm • Average over previous scale and subband estimates to improve estimation

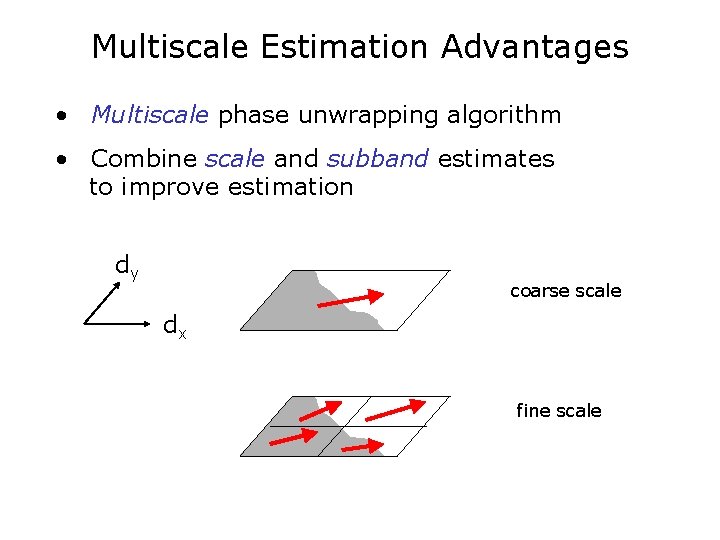
Multiscale Estimation Advantages • Multiscale phase unwrapping algorithm • Combine scale and subband estimates to improve estimation dy coarse scale dx fine scale

Image Flow Estimation Result

Summary • Development of DT-CWT and quaternion wavelet transform (DT-QWT) DWT [e. g. , Daubechies] 1 -D HT and analytic signal 1 -D DT-CWT [Lina, Kingsbury, Selesnick, …] 2 -D HT and analytic signal (complex / quaternion) 2 -D DT-CWT DT-QWT [Kingsbury, Selesnick, …] [Chan, Choi, Baraniuk]

Conclusions • Developed QWT for image analysis • Fast, “multiscale” • QWT phase and Shift Theorem • Multiscale flow estimation through QWT phase • Local QFT analysis (details in thesis) • Future Directions • Hypercomplex wavelets (3 -D or higher) • Image compression [Ates, Orchard, …]