Coherent Diffraction Imaging a novel and promising tool

Coherent Diffraction Imaging - a novel and promising tool to investigate non crystalline matter at atomic resolution Dr. Cinzia Giannini CNR - Istituto di Cristallografia BARI Email: cinzia. giannini@ic. cnr. it

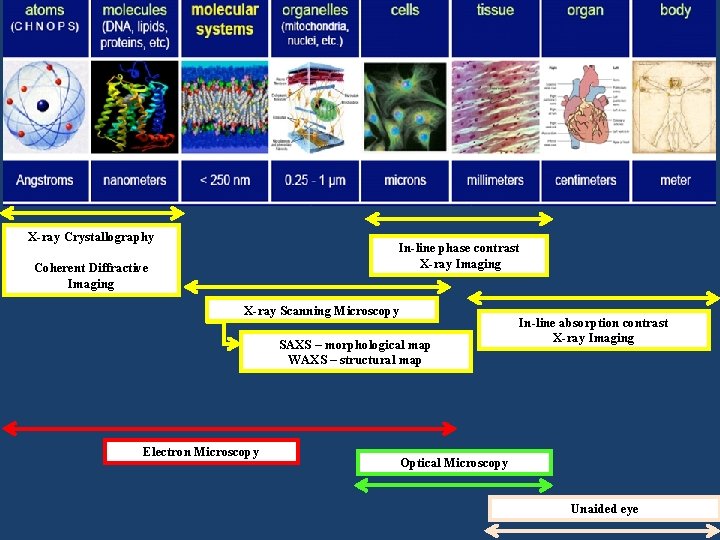
X-ray Crystallography In-line phase contrast X-ray Imaging Coherent Diffractive Imaging X-ray Scanning Microscopy SAXS – morphological map WAXS – structural map Electron Microscopy In-line absorption contrast X-ray Imaging Optical Microscopy Unaided eye

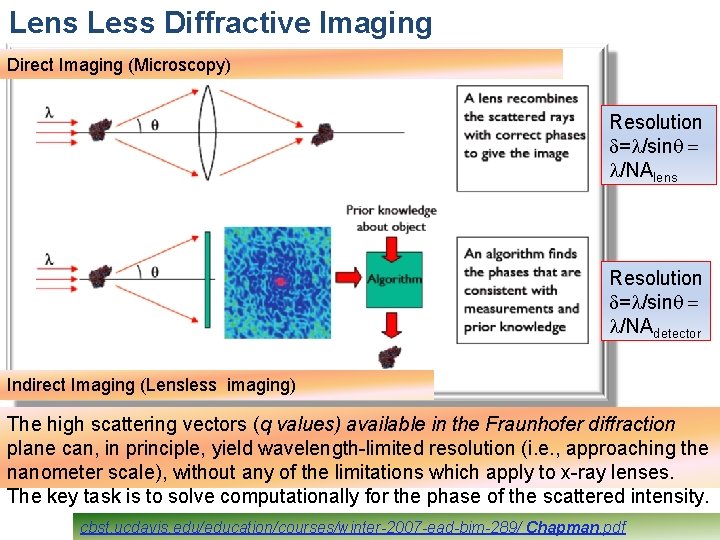
Lens Less Diffractive Imaging Direct Imaging (Microscopy) Resolution d=l/sinq = l/NAlens Resolution d=l/sinq = l/NAdetector Indirect Imaging (Lensless imaging) The high scattering vectors (q values) available in the Fraunhofer diffraction plane can, in principle, yield wavelength-limited resolution (i. e. , approaching the nanometer scale), without any of the limitations which apply to x-ray lenses. The key task is to solve computationally for the phase of the scattered intensity. cbst. ucdavis. edu/education/courses/winter-2007 -ead-bim-289/ Chapman. pdf

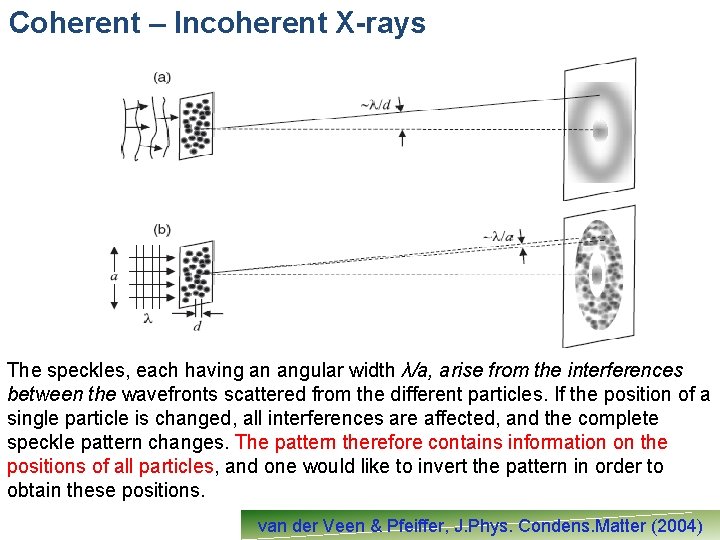
Coherent – Incoherent X-rays The speckles, each having an angular width λ/a, arise from the interferences between the wavefronts scattered from the different particles. If the position of a single particle is changed, all interferences are affected, and the complete speckle pattern changes. The pattern therefore contains information on the positions of all particles, and one would like to invert the pattern in order to obtain these positions. van der Veen & Pfeiffer, J. Phys. Condens. Matter (2004)

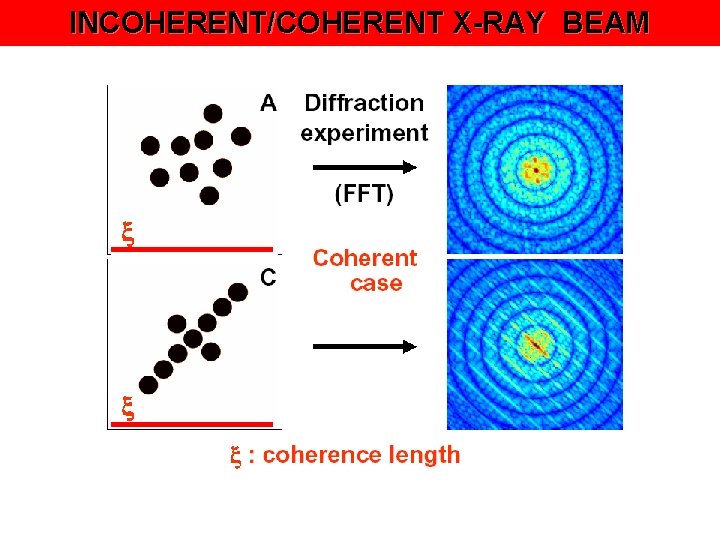
INCOHERENT/COHERENT X-RAY BEAM

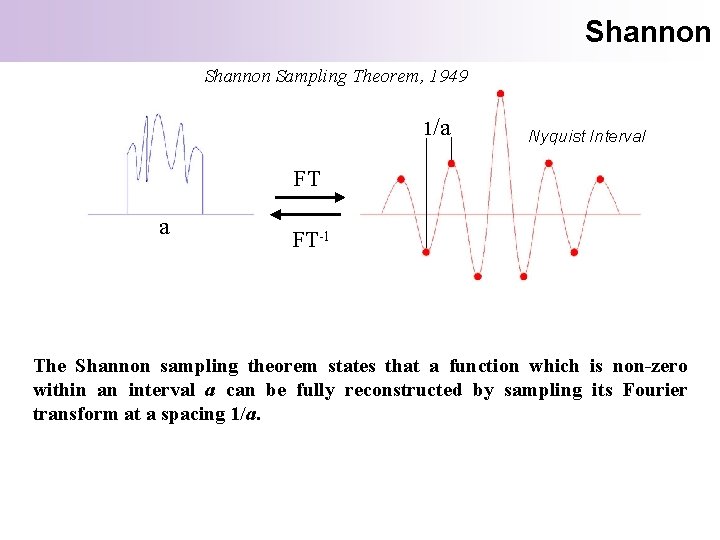
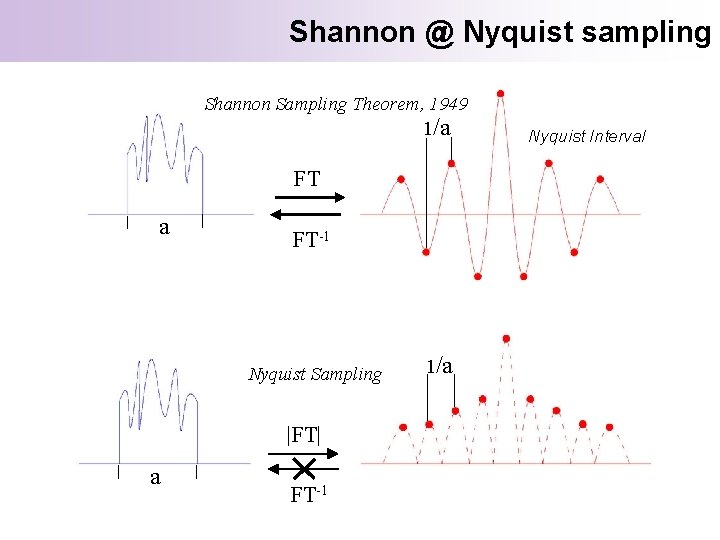
Shannon Sampling Theorem, 1949 1/a Nyquist Interval FT a FT-1 The Shannon sampling theorem states that a function which is non-zero within an interval a can be fully reconstructed by sampling its Fourier transform at a spacing 1/a.

Shannon @ Nyquist sampling Shannon Sampling Theorem, 1949 1/a FT-1 Nyquist Sampling |FT| a FT-1 1/a Nyquist Interval

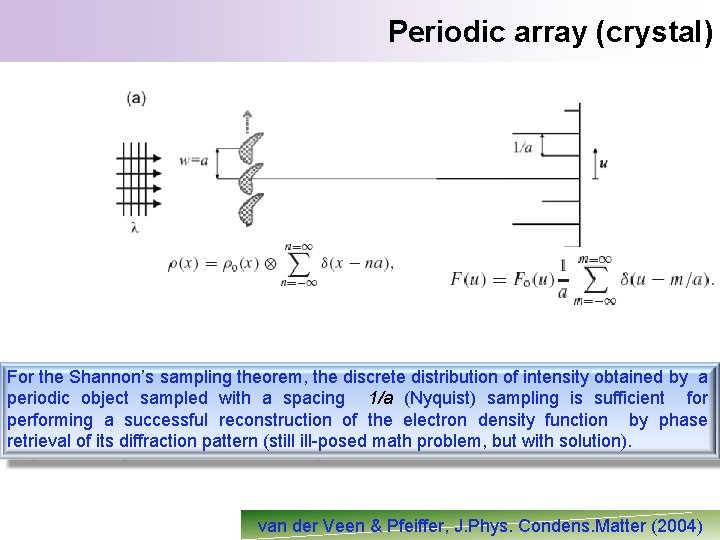
Periodic array (crystal) For the Shannon’s sampling theorem, the discrete distribution of intensity obtained by a periodic object sampled with a spacing 1/a (Nyquist) sampling is sufficient for performing a successful reconstruction of the electron density function by phase retrieval of its diffraction pattern (still ill-posed math problem, but with solution). van der Veen & Pfeiffer, J. Phys. Condens. Matter (2004)

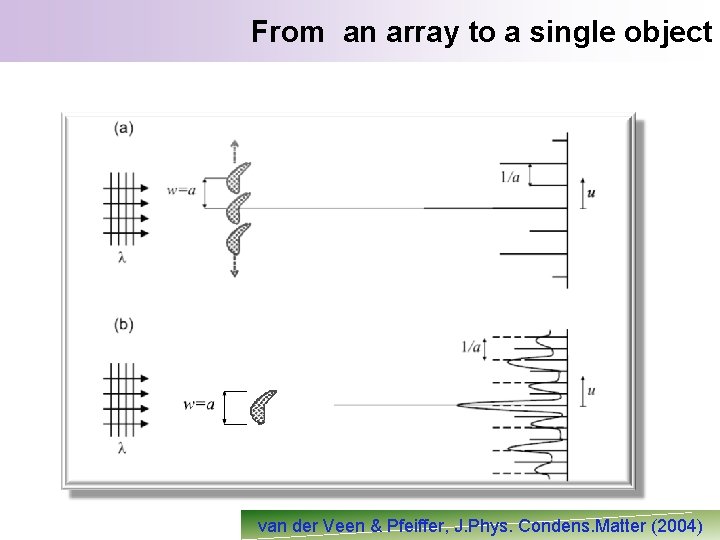
From an array to a single object van der Veen & Pfeiffer, J. Phys. Condens. Matter (2004)

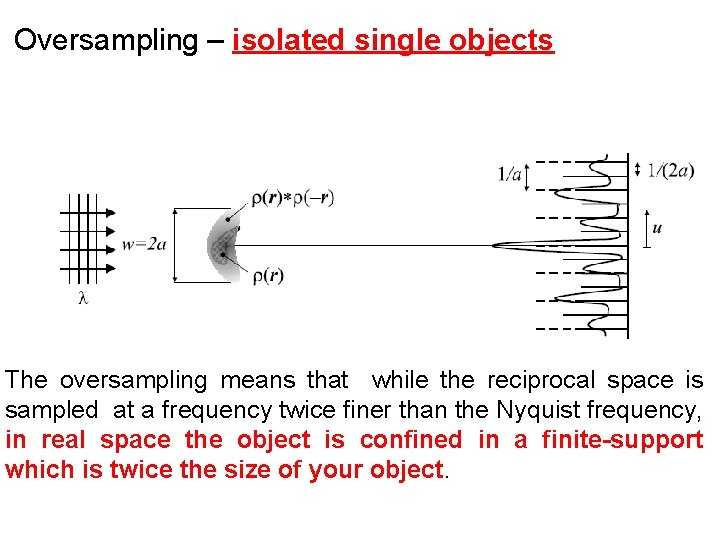
Oversampling – isolated single objects The oversampling means that while the reciprocal space is sampled at a frequency twice finer than the Nyquist frequency, in real space the object is confined in a finite-support which is twice the size of your object.

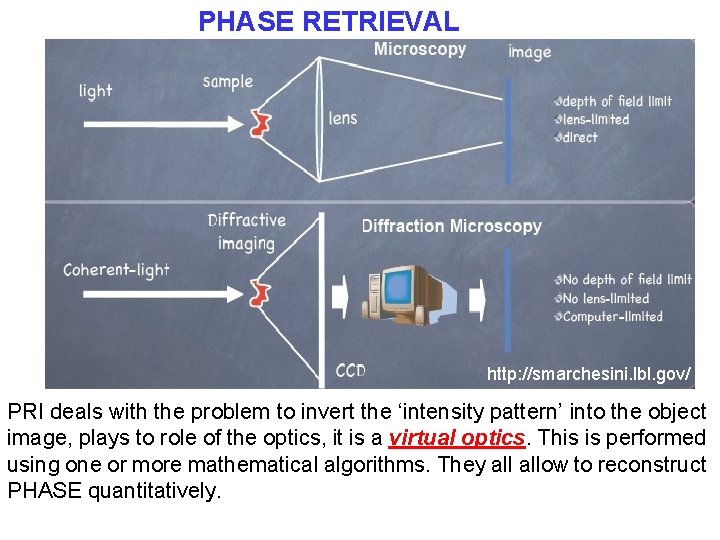
PHASE RETRIEVAL IMAGING (PRI) http: //smarchesini. lbl. gov/ PRI deals with the problem to invert the ‘intensity pattern’ into the object image, plays to role of the optics, it is a virtual optics. This is performed using one or more mathematical algorithms. They allow to reconstruct PHASE quantitatively.

THE FIRST EXPERIMENTAL DEMONSTRATION 2 D reconstruction ~ 75 nm resolution (a) SEM image (b) An oversampled (c) An image diffraction reconstructed from (b). pattern (in a log scale) from (a). The specimen was a collection of gold dots, each 100 nm in diameter and 80 nm thick, deposited on a 100 -nm-thick silicon nitride membrane, to form a set of six letters (a). This specimen was illuminated with l =1. 7 nm monochromatic and parallel X-rays from the X 1 A undulator beamline at the National Synchrotron Light Source.

FIRST HIGH RESOLUTION 3 D X-RAY BURIED STRUCTURES A double layered sample made of Ni (2. 7 x 2. 5 x 1 mm 3) DIFFRACTION MICROSCOPY The sample, fabricated by electron beam lithography, consists of two single-layered Ni patterns (each with a size of 2. 5 x 2 x 0. 1 mm) rotated relatively 65° to each other in-plane and separated by a distance of 1 mm. The sample is supported by a thin silicon nitride membrane window. Figure 1(a) shows a scanning electron microscopy (SEM) image of the sample. Because of the 1 mm separation of the two layers, the SEM image shows the pattern in the top layer, and the pattern in the bottom layer is visible only as a soft blur. The 3 D reconstruction has been carried out using a series of thirty-one 2 D diffraction patterns recorded from the sample with the rotation angles ranging from -75 ° to +75 ° in 5° increments. 3 D RECONSTRUCTION ON BURIED NANOSTRUCTURES (2 D resolution ~ 8 nm; 3 D resolution ~ 50 nm) Undulator beam line at SPring-8 with a wavelength of 0. 2 nm. A 150 mm horizontal slit at a distance of 27 m upstream of the sample J. Miao, T. Ishikawa, B. Johnson, E. H. Anderson, B. Lai, and K. O Phys. Rev. Lett. 89, 088303 (2002)

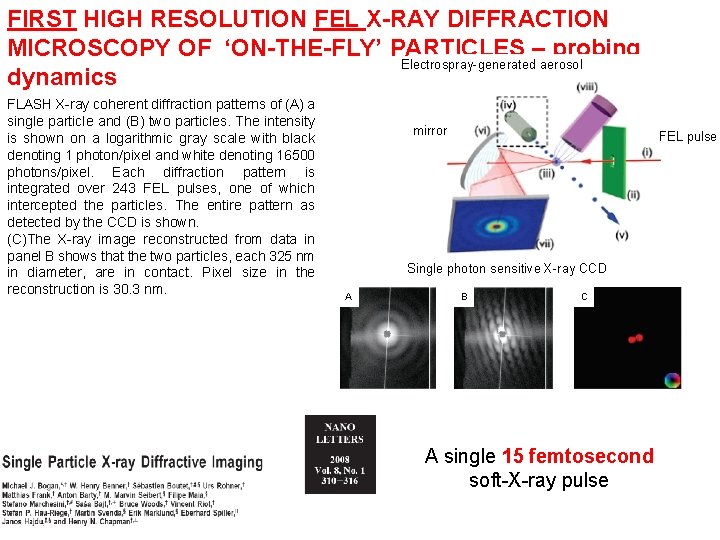
FIRST HIGH RESOLUTION FEL X-RAY DIFFRACTION MICROSCOPY OF ‘ON-THE-FLY’ PARTICLES – probing Electrospray-generated aerosol dynamics FLASH X-ray coherent diffraction patterns of (A) a single particle and (B) two particles. The intensity is shown on a logarithmic gray scale with black denoting 1 photon/pixel and white denoting 16500 photons/pixel. Each diffraction pattern is integrated over 243 FEL pulses, one of which intercepted the particles. The entire pattern as detected by the CCD is shown. (C)The X-ray image reconstructed from data in panel B shows that the two particles, each 325 nm in diameter, are in contact. Pixel size in the reconstruction is 30. 3 nm. mirror FEL pulse Single photon sensitive X-ray CCD A B C A single 15 femtosecond soft-X-ray pulse

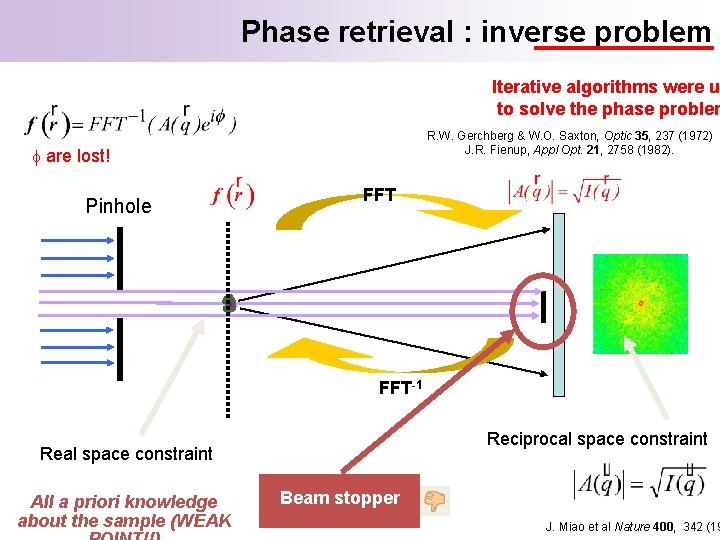
Phase retrieval : inverse problem Iterative algorithms were us to solve the phase problem R. W. Gerchberg & W. O. Saxton, Optic 35, 237 (1972) J. R. Fienup, Appl Opt. 21, 2758 (1982). are lost! Pinhole FFT-1 Reciprocal space constraint Real space constraint All a priori knowledge about the sample (WEAK Beam stopper J. Miao et al Nature 400, 342 (19

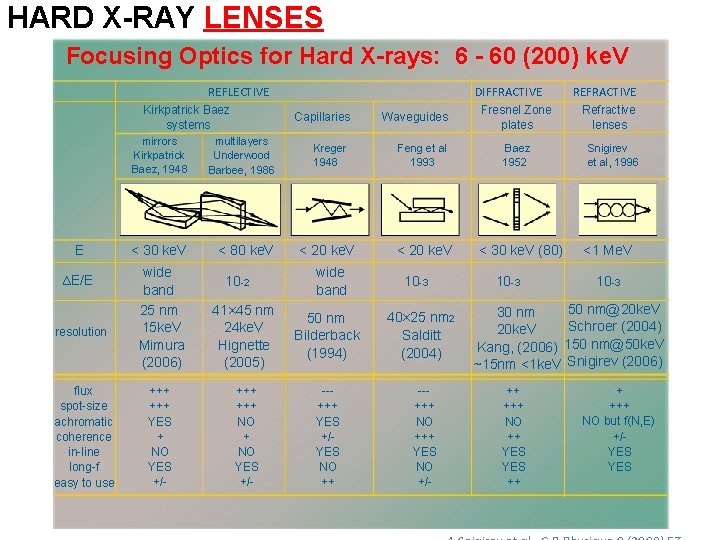
HARD X-RAY LENSES Focusing Optics for Hard X-rays: 6 - 60 (200) ke. V REFLECTIVE Kirkpatrick Baez systems E ∆E/E resolution flux spot-size achromatic coherence in-line long-f easy to use DIFFRACTIVE Capillaries mirrors Kirkpatrick Baez, 1948 multilayers Underwood Barbee, 1986 < 30 ke. V < 80 ke. V Kreger 1948 < 20 ke. V wide band 25 nm 15 ke. V Mimura (2006) 41× 45 nm 24 ke. V Hignette (2005) 50 nm Bilderback (1994) +++ YES + NO YES +/- +++ NO YES +/- --+++ YES +/YES NO ++ 10 -2 wide band Waveguides Feng et al 1993 < 20 ke. V 10 -3 40× 25 nm 2 Salditt (2004) --+++ NO +++ YES NO +/- Fresnel Zone plates Baez 1952 < 30 ke. V (80) 10 -3 REFRACTIVE Refractive lenses Snigirev et al, 1996 <1 Me. V 10 -3 50 nm@20 ke. V 30 nm Schroer (2004) 20 ke. V Kang, (2006) 150 nm@50 ke. V ~15 nm <1 ke. V Snigirev (2006) ++ +++ NO ++ YES ++ + +++ NO but f(N, E) +/YES

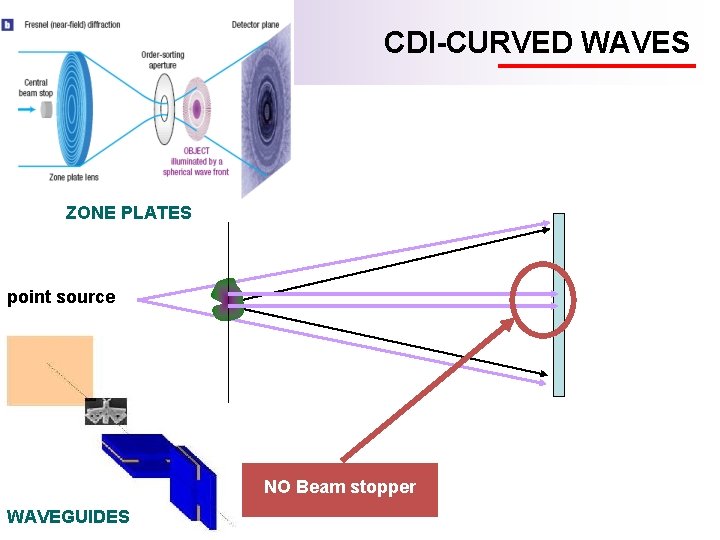
CDI-CURVED WAVES ZONE PLATES point source NO Beam stopper WAVEGUIDES

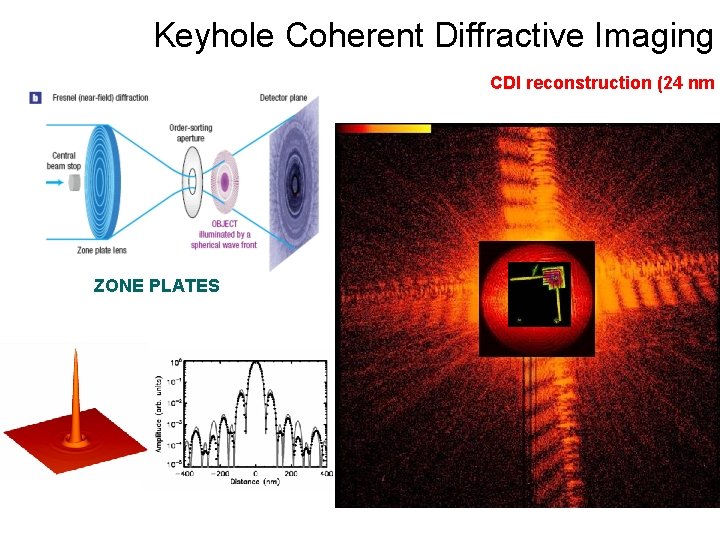
Keyhole Coherent Diffractive Imaging In Keyhole (Fresnel) CDI a finite, diverging beam, is used to as support of the phasing retrieval process.

Keyhole Coherent Diffractive Imaging CDI reconstruction (24 nm r ZONE PLATES

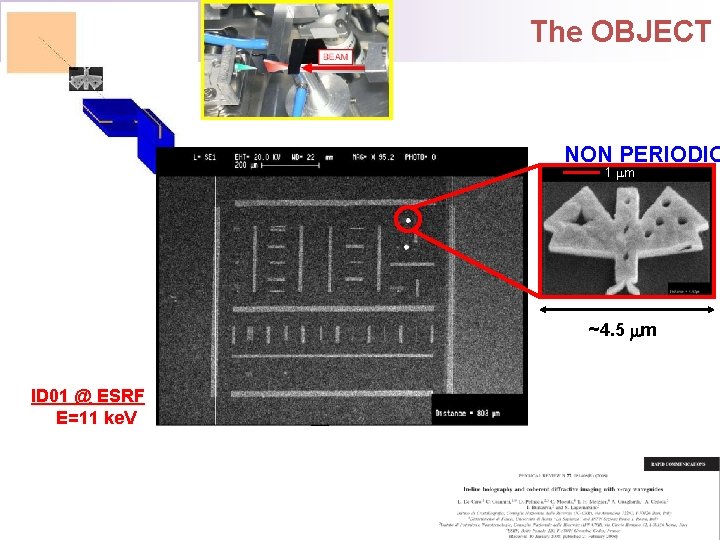
HOLOGRAPHY & CDI with TWO CROSSED Waveguides ID 01 @ ESRF SOURCE SIZE ~ 200 x 200 nm 2

The OBJECT NON PERIODIC 1 m ~4. 5 mm ID 01 @ ESRF E=11 ke. V

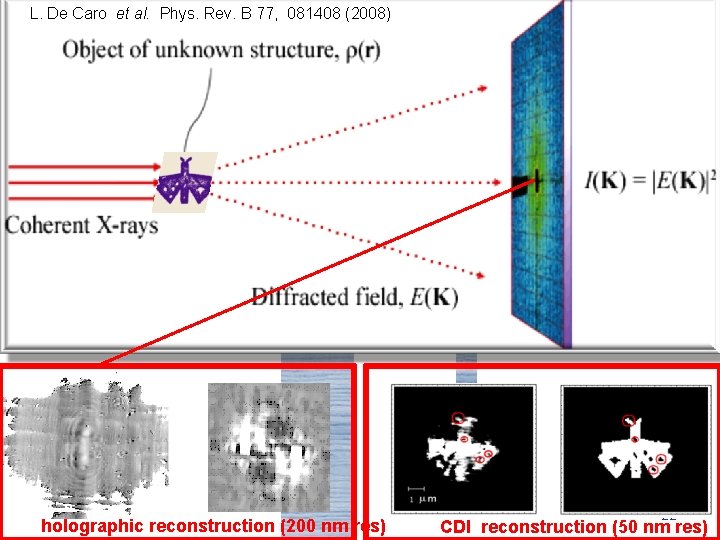
L. De Caro et al. Phys. Rev. B 77, 081408 (2008) holographic reconstruction (200 nm res) 22 CDI reconstruction (50 nm res)

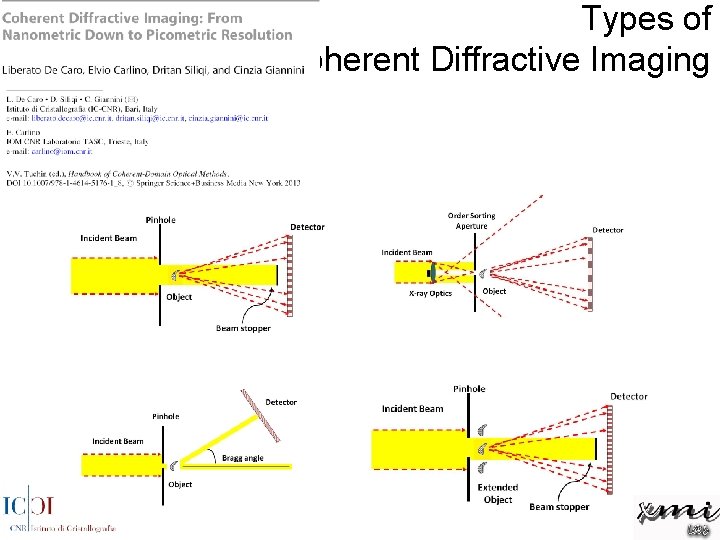
Types of Coherent Diffractive Imaging

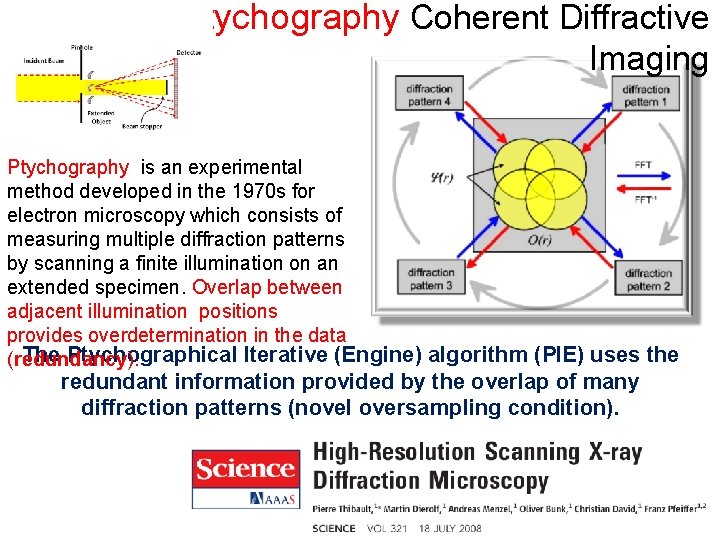
Ptychography Coherent Diffractive Imaging Ptychography is an experimental method developed in the 1970 s for electron microscopy which consists of measuring multiple diffraction patterns by scanning a finite illumination on an extended specimen. Overlap between adjacent illumination positions provides overdetermination in the data The Ptychographical Iterative (Engine) algorithm (PIE) uses the (redundancy). redundant information provided by the overlap of many diffraction patterns (novel oversampling condition).

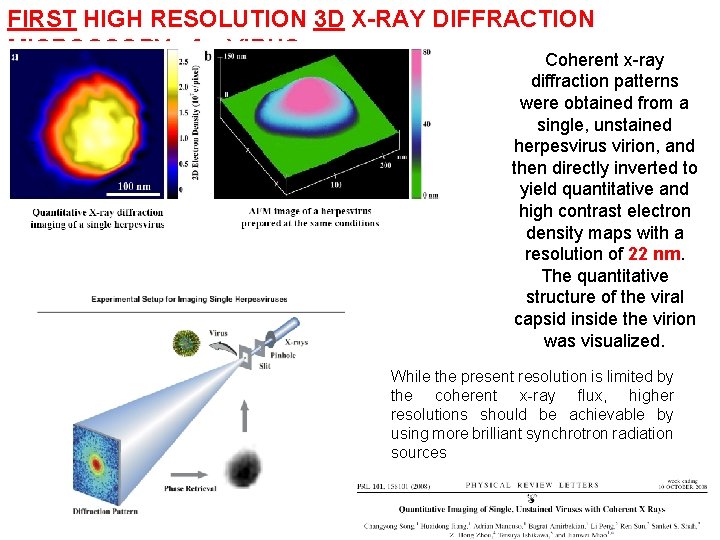
FIRST HIGH RESOLUTION 3 D X-RAY DIFFRACTION MICROSCOPY of a VIRUS Coherent x-ray diffraction patterns were obtained from a single, unstained herpesvirus virion, and then directly inverted to yield quantitative and high contrast electron density maps with a resolution of 22 nm. The quantitative structure of the viral capsid inside the virion was visualized. While the present resolution is limited by the coherent x-ray flux, higher resolutions should be achievable by using more brilliant synchrotron radiation sources

Dose problems The x-ray dose needed to image a single molecule is much larger than the dose required to completely destroy the molecule through radiation damage processes. X-ray crystallographers mitigate this problem by spreading the damage over billions of molecules in a single crystal. Since the molecules are all identical and precisely aligned in the crystal, the x-ray scattering information is preserved and the structure can be determined. FEL X-ray pulse could be focused onto a single molecule, which would be destroyed – but not before the scattered x-rays are already on their way to the detector carrying the information needed to deduce the image. Allowing: 3 D imaging at or near atomic resolution of non-crystalline biomolecules (e. g. viruses, large protein molecular machines), nanoparticles (e. g. quantum dots), and amorphous and disordered materials. 3 D structure determination of nanocrystals and ordered 2 D structures (e. g. biomembranes) 3 D characterization of strains and defects in crystals, dislocation and deformation

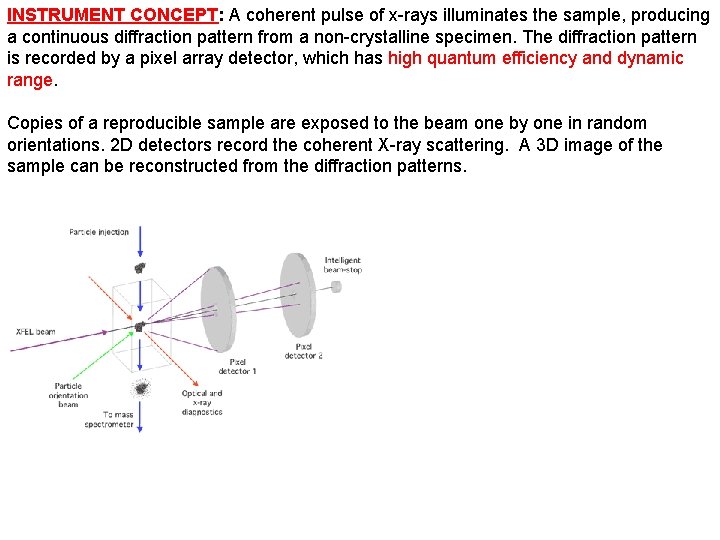
INSTRUMENT CONCEPT: A coherent pulse of x-rays illuminates the sample, producing a continuous diffraction pattern from a non-crystalline specimen. The diffraction pattern is recorded by a pixel array detector, which has high quantum efficiency and dynamic range. Copies of a reproducible sample are exposed to the beam one by one in random orientations. 2 D detectors record the coherent X-ray scattering. A 3 D image of the sample can be reconstructed from the diffraction patterns.

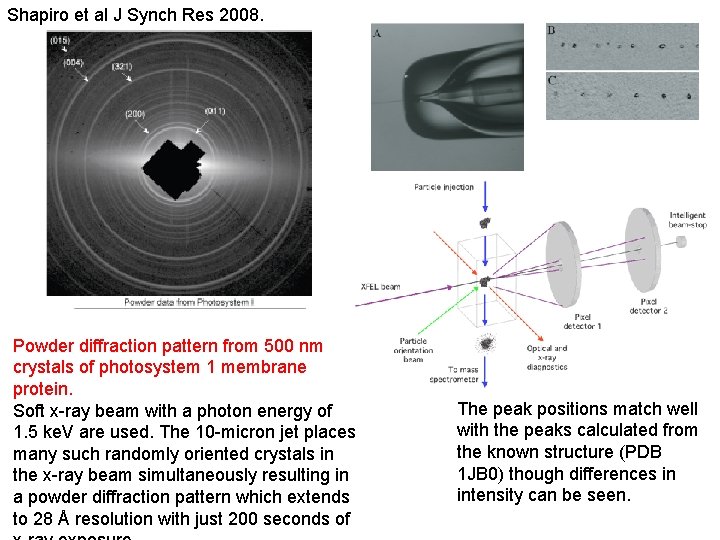
X-ray Powder Diffraction from Sub-micron Crystals of Photosystem-1 Membrane Protein Shapiro et al J Synch Res 2008.

Shapiro et al J Synch Res 2008. Powder diffraction pattern from 500 nm crystals of photosystem 1 membrane protein. Soft x-ray beam with a photon energy of 1. 5 ke. V are used. The 10 -micron jet places many such randomly oriented crystals in the x-ray beam simultaneously resulting in a powder diffraction pattern which extends to 28 Å resolution with just 200 seconds of The peak positions match well with the peaks calculated from the known structure (PDB 1 JB 0) though differences in intensity can be seen.

Membrane proteins constitute >30% of the proteins in an average cell, and yet the number of currently known structures of unique membrane proteins is <300. To develop new concepts for membrane protein structure determination, SERIAL NANOCRYSTALLOGRAPHY METHOD, was introduced in which fully hydrated protein nanocrystals are delivered to an x-ray beam within a liquid jet at room temperature. Serial nanocrystallography overcomes the problem of x-ray damage, which is currently one of the major limitations for x-ray structure determination of small crystals. By combining serial nanocrystallography with x-ray free-electron laser sources in the future, it may be possible to produce molecular-resolution electron-density maps using membrane protein crystals that contain only a few hundred or thousand unit cells.

Bragg Coherent Diffractive Imaging

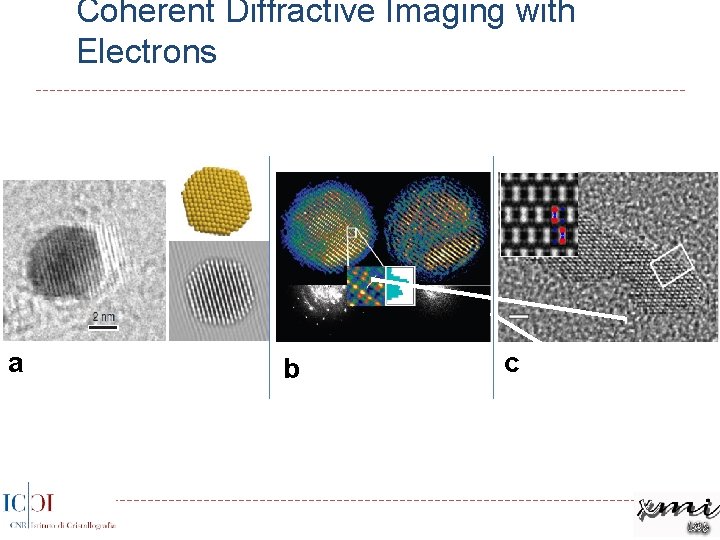
Coherent Diffractive Imaging with Electrons a b c

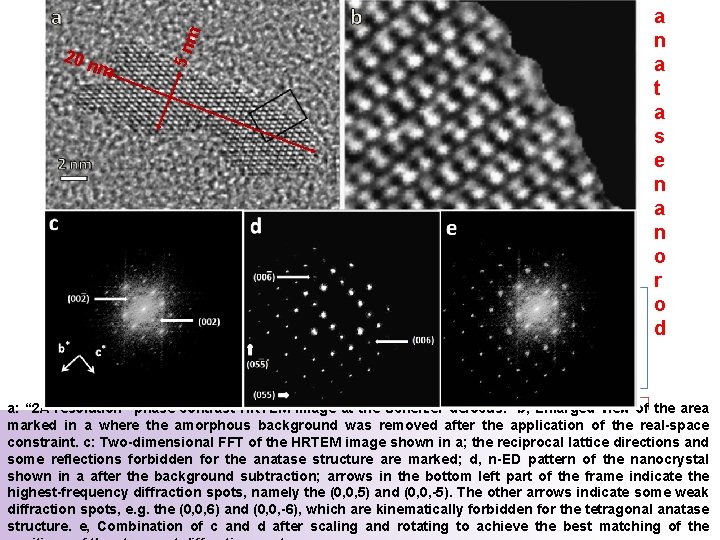
m 5 n 20 n m a n a t a s e n a n o r o d a: “ 2 A-resolution” phase-contrast HRTEM image at the Scherzer defocus. b, Enlarged view of the area marked in a where the amorphous background was removed after the application of the real-space constraint. c: Two-dimensional FFT of the HRTEM image shown in a; the reciprocal lattice directions and some reflections forbidden for the anatase structure are marked; d, n-ED pattern of the nanocrystal shown in a after the background subtraction; arrows in the bottom left part of the frame indicate the highest-frequency diffraction spots, namely the (0, 0, 5) and (0, 0, -5). The other arrows indicate some weak diffraction spots, e. g. the (0, 0, 6) and (0, 0, -6), which are kinematically forbidden for the tetragonal anatase structure. e, Combination of c and d after scaling and rotating to achieve the best matching of the

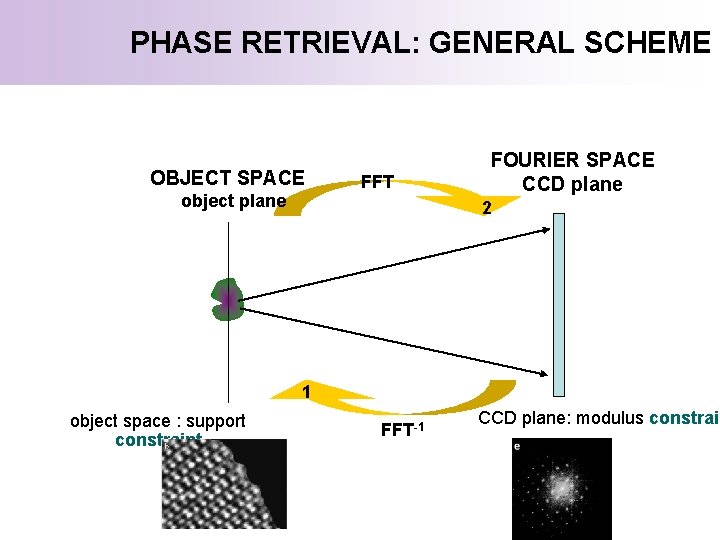
PHASE RETRIEVAL: GENERAL SCHEME OBJECT SPACE object plane FFT FOURIER SPACE CCD plane 2 1 object space : support constraint FFT-1 CCD plane: modulus constrain

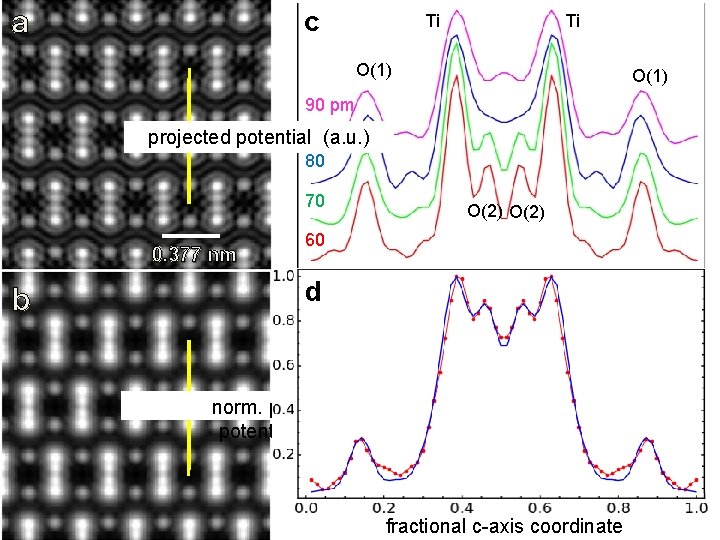
Phase-retrieved diffractive image - original HRTEM data NO ABERRATION CORRECTOR resolution of 70 pm

a c Ti Ti O(1) 90 pm projected potential (a. u. ) 80 70 0. 377 nm b O(2) 60 d norm. projected potential fractional c-axis coordinate

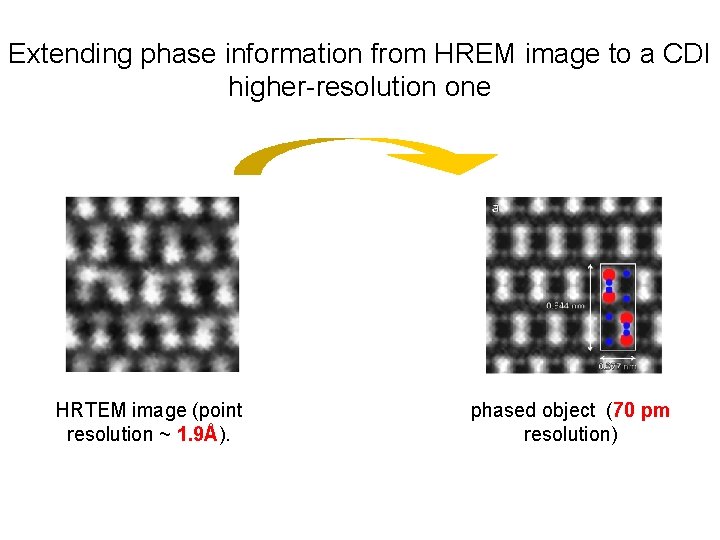
Extending phase information from HREM image to a CDI higher-resolution one HRTEM image (point resolution ~ 1. 9Å). phased object (70 pm resolution)

Perspectives: HYBRID nanocrystals Au@Fe 3 O 4 a b Cd. S-Pb. Se matchstick core@shell Shi, W. et al, Nano Lett 2006, 6, 875 Kudera et al, Nano Lett. 2005, 5, 445 20 nm nm 20 Au-Fe 3 O 4 c Au-Cd. Se-Au d dumbbells flowers Yu, H. et al. Nano Lett. 2005, 5, 379. Cd. S-Fe. Pt Mokari et al. , Science 2004, 304, 1787 e f Fe 3 O 4 -Au-Fe 3 O 4 hetero-dimers Gu, H. et al. J. Am. Chem. Soc. 2004, 126, 5664 hetero-oligomers 20 nm Shi, W. . et al, Nano Lett 2006, 6, 875

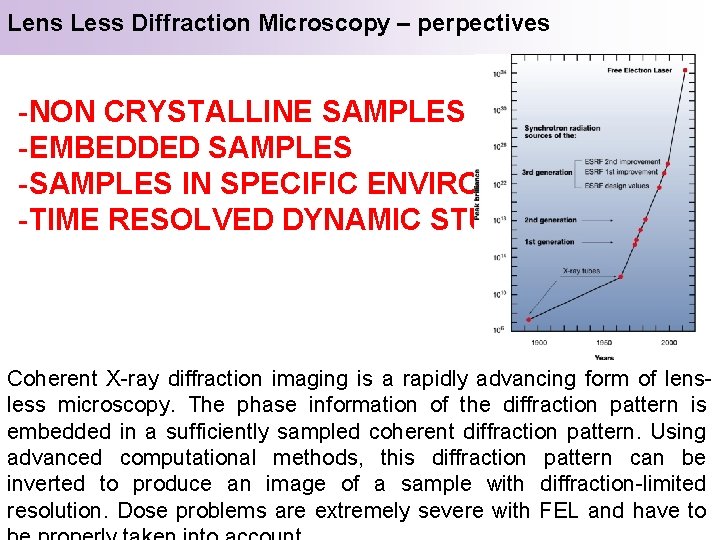
Lens Less Diffraction Microscopy – perpectives -NON CRYSTALLINE SAMPLES (BIO) -EMBEDDED SAMPLES -SAMPLES IN SPECIFIC ENVIROMENTS -TIME RESOLVED DYNAMIC STUDIES Coherent X-ray diffraction imaging is a rapidly advancing form of lensless microscopy. The phase information of the diffraction pattern is embedded in a sufficiently sampled coherent diffraction pattern. Using advanced computational methods, this diffraction pattern can be inverted to produce an image of a sample with diffraction-limited resolution. Dose problems are extremely severe with FEL and have to