Cognitive Computing 2012 Consciousness and Computation computing machinery

Cognitive Computing: 2012 Consciousness and Computation: computing machinery & intelligence 3. EMULATION Mark Bishop

The Universal Machine Norma l Thesis: “With suitable coding of data, every algorithm can be represented as a flowchart program for NORMA. ” l But how? Some obvious criticisms of NORMA include. . . l 1: NORMA does not define enough operations and tests: § l 2: NORMA data types are too restricted: § l § 9/10/2021 No mechanism for procedures. At the very least one needs to be able to refer to labels indirectly so that sub-routines can be constructed. 5: Other criticisms include: § l No provision for ARRAYs of numbers. 4: The restriction to flowchart programs is too restrictive: § l No provision for negative or floating point numbers. 3: Access to data is too restricted: § l No assignment, multiply, subtract, divide etc. The lack of string handling. No logical shifts etc. The criticisms [1. . 4] are considered the most important. (c) Bishop: Consciousness and Computations 2

Informal ‘proof’ of thesis l To demonstrate that every algorithm can be coded as a NORMA flowchart program it is necessary to show each of the main criticisms [1. . 4] can be answered. l Specify a new machine NORMA+ which has the desired feature. l Show any program in NORMA+ can be –recoded as a flowchart program for NORMA. 9/10/2021 (c) Bishop: Consciousness and Computations 3

Answer to 1 st criticism l Assignment to a constant (eg. A : = 0) l Theorem: “Every WHILE program can be mapped onto a corresponding flowchart program”. WHILE (A <> 0) DO A : = A -1; END; This WHILE program can be written as a ‘macro’. Similar macros can be written for (A : = 1), (A : = 2) etc. 9/10/2021 (c) Bishop: Consciousness and Computations 4

Addition A : = A + B using [a]; Consider a macro to calculate (A : = A + B). We need to use an extra register a, hence we write the macro as {A : = A + B using a} a : = 0; WHILE (B <> 0) DO {adds B into A and makes a copy of B} A : = A + 1; a : = a + 1; B : = B - 1; END; WHILE (a <> 0) DO {resets B to original value} a : = a - 1; B : = B + 1; END; 9/10/2021 (c) Bishop: Consciousness and Computations 5

Assignment to a register A : = B using [a]; A : = 0; A : = A + B using a; 9/10/2021 (c) Bishop: Consciousness and Computations 6

Subtraction A : = A - B using [a, b]; a : = B using b; WHILE (a <> 0) DO A : = A - 1; a : = a - 1; END; 9/10/2021 (c) Bishop: Consciousness and Computations 7

Register Test Operations 1 ? (A < 2) using [a, b]; IF ? (A < 2) THEN L 2: TRUE ELSE L 1: FALSE END; a : = A using b; IF (a = 0) THEN GOTO L 2; a : = a - 1; IF (a = 0) THEN GOTO L 2; L 1: FALSE; L 2: TRUE; 9/10/2021 (c) Bishop: Consciousness and Computations 8

Multiplication A : = A x B using a, b, c; a : = A using b; b : = B using c; A : = 0; WHILE (b <> 0) DO A : = A + a using c; b : = b - 1; END; 9/10/2021 (c) Bishop: Consciousness and Computations 9

Division A : = A DIV B using [a. . e]; {Remainder held in e} e : = A using a; A : = 0; WHILE (e >= B using [a. . c]) DO e : = e - B using d; {[a. . c] still in use} INC A END; 9/10/2021 (c) Bishop: Consciousness and Computations 10

NORMA and primes: on testing for integer division Div (A, B)? {True iff A is exactly divisible by B} a : = A; WHILE (a >= B) DO a : = a – B; IF (a = 0) THEN GOTO Label-Divisible ELSE GOTO Label-NOT-Divisible 9/10/2021 (c) Bishop: Consciousness and Computations 11

On the testing for prime a. Prime (A)? {NB. Zero and one are neither prime nor composite} IF (A < 2) THEN GOTO [Label-NOT-Prime] j : = A - 1; WHILE NOT (Div (A, j) DO j : = j – 1; IF (j = 1) THEN GOTO [Label-Prime] ELSE GOTO [Label-NOT-Prime] 9/10/2021 (c) Bishop: Consciousness and Computations 12

On calculating the kth prime A : = PRIME (K) {Stores the Kth prime in A, where the 1 st prime is 2} A : = 0; k : = K; WHILE (k <> 0) DO k : = k – 1; A : = A + 1; WHILE NOT ( a. Prime (A) ) DO A : = A + 1; END; 9/10/2021 (c) Bishop: Consciousness and Computations 13

Answer to criticism 2 Representing negative numbers An arbitrary integer m can easily be represented as the order pair (n, d) of non negative integers: n = |m| d = 0 IF (m >= 0) d = 1 otherwise 9/10/2021 (c) Bishop: Consciousness and Computations 14

Representing fixed length real numbers l Using a similar idea to that used for negative numbers, operations on a non negative rational number r can be defined in terms of the ordered pair (a, b), where (b > 0) and (r = a/b). l Since arithmetic on rationals conforms to the following rules: l Addition & Subtraction l l Multiplication l l 9/10/2021 (a, b) / (c, d) = (ad, bc) iff (c <> 0) Equality l l (a, b) × (c, d) = (ac, bd) Division l l (a, b) ± (c, d) = (ad ± bc, bd) ? ((a, b) = (c, d)) iff (ad = bc) . . . there is no problem constructing appropriate NORMA programs using fixed length reals. (c) Bishop: Consciousness and Computations 15

Answer to 3 rd criticism • To answer criticism 3 we define a new machine SAM (Simple Array Machine) with more flexible access to data. • SAM augments NORMA by possessing the array of registers, A[1], A [2]. . A [n] • • in addition to the standard registers A, B. . Y, which are now referred to as index registers. The operations defined by SAM are those of NORMA plus the array operations: • • 9/10/2021 A [J] : = A [J] + 1; A [J] : = A [J] - 1; where J is any index register. A [n] : = A [n] + 1; A [n] : = A [n] - 1; where n is any positive integer. (c) Bishop: Consciousness and Computations 16

Array test operations l SAM also has the array test operations: ? (A [J] = 0) ? (A [n] = 0) l SAMs input and output functions are the same as NORMAs except that the input function also initialises each array register to zero. 9/10/2021 (c) Bishop: Consciousness and Computations 17

Theorem 2: NORMA can simulate SAM l Proof: We have to show any given program P for SAM can be translated into a NORMA program Q such that: l l NORMA (Q) = SAM (P) Method: Pack all of SAM array into a single NORMA register. l If at some stage in the computation a SAM array contains [a 1, a 2, . . an] then at the equivalent stage a NORMA register will contain A. l A = P 1 a 1 × P 2 a 2 × P 3 a 3. . . × Pnan, where Pj = jth prime. 9/10/2021 (c) Bishop: Consciousness and Computations 18

Increment indexed array l To define Q from P, we translate each SAM instruction into a sequence of NORMA instructions as follows: l l All index register instructions are left unchanged. Array operations of the form A [J] : = A [J] + 1 are translated into: l l l B : = PRIME (J); A : = A × B Where PRIME is the PRIME number function defined earlier. 9/10/2021 (c) Bishop: Consciousness and Computations 19

Decrement indexed array l Array operations of the form A [J] : = A [J] - 1 are translated into: B : = PRIME (J); A : = A DIV B; Where DIV is a special integer division defined by: a DIV b= a / b =a 9/10/2021 If b divides exactly into a otherwise (c) Bishop: Consciousness and Computations 20

Testing an array element l A test of the form ? (A [J] <> 0) is translated into: B : = PRIME (J) RETURN div (A, B) Where div (A , B) is TRUE when A is exactly divisible by B and FALSE otherwise. ie. The test div (A, B) will return TRUE just in the case that A [J] ≠ 0. 9/10/2021 (c) Bishop: Consciousness and Computations 21

INC and DEC array using a constant index, n l An operation of the form (A [n] = A [n] + 1) is translated into: B : = PRIME (n); A : = A × B; l Similarly (A [n] = A [n] - 1) is translated into: B : = PRIME (n); A : = A DIV B; 9/10/2021 (c) Bishop: Consciousness and Computations 22

Proof of theorem 2 l The test ? (A [n] = 0) uses the test div (Pn, A) to RETURN the correct value, where Pn = PRIME (n). l Now each operation and test of Q must be replaced by the corresponding NORMA macro; l And if we ensure that Q initially sets A to 1 to represent the input condition of SAMs array then … l … the simulation clearly works and hence Theorem 2 is proved. 9/10/2021 (c) Bishop: Consciousness and Computations 23

Answer to criticism 4 - only flowcharts l To answer criticism 4 we need to define a new machine SIM (Simple Indirect Machine). l In a SIM program P with labels (1. . l. . k), the operations defined by SIM are those given by NORMA plus the following two Indirect Jump calls: l: GOTO (A); {GOTO a where a is the content of register A} l: IF (T) THEN GOTO (A); 9/10/2021 {IF TRUE GOTO label a} (c) Bishop: Consciousness and Computations 24

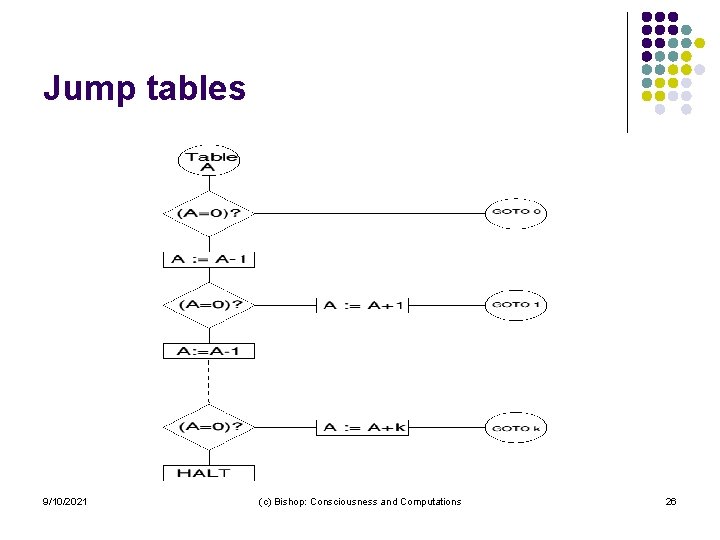
Theorem 3: NORMA can simulate SIM l Proof: We have to show any given program P for SIM can be translated into a NORMA program Q such that: l l NORMA (Q) = SIM (P) Method: Use a Jump Table. l 9/10/2021 For each register (eg. A) that appears in the program we need to define an extra segment of code, table. A. (c) Bishop: Consciousness and Computations 25

Jump tables 9/10/2021 (c) Bishop: Consciousness and Computations 26

For the SIM Indirected jump l This extra code can be added after instruction k of SIM program P. l We can now replace the new SIM instructions by the following NORMA code: l SIM l l: GOTO (A); l NORMA l l: GOTO table. A; {Where table. A is label of jump table for the A reg} 9/10/2021 (c) Bishop: Consciousness and Computations 27

The SIM indirected test l SIM l l l: IF (T) THEN GOTO (A); NORMA l l l: IF (T) THEN GOTO table. A; {Where table. A is label of the jump table for the A register} l Now each operation and test of SIM Q must be replaced by the corresponding NORMA macro. l It is now clear that the resulting NORMA program Q is equivalent to the SIM program P. l The simulation clearly works and hence Theorem 3 is proved. 9/10/2021 (c) Bishop: Consciousness and Computations 28

HOMEWORK: Implement NORMA_STACK l l Prove that the machine NORMA_STACK is no more powerful than the universal machine NORMA by designing two MACROs to implement: l (a) X=POP which removes the top value from the STACK and places it into the X register; l (b) PUSH (X) which places the contents of the X register on to the top of the STACK; and submit a short (no more than 1 -page) report detailing their operation. 9/10/2021 (c) Bishop: Consciousness and Computations 29