COEN 351 ECommerce Security Essentials of Cryptography Cryptography

COEN 351 E-Commerce Security Essentials of Cryptography

Cryptography n n Scrambles a plain-text into crypto-text. Enables to descramble plain text.

Symmetric Cryptography n Uses the same key for encryption, decryption

Asymmetric Cryptography n Uses different key for encryption, decryption

Message Authentication Codes n Condenses message into a short hash • SHA 1, … MD 5, … are appropriate cryptographically secure hash functions • For example, encrypt only the MAC with a key known to sender and receiver.

Message Authentication Code n n Alternatively, use a secret key. This also provides authentication.

Use of Asymmetric Cryptography n Generic idea: Make one key public. n How? n Website n n On your business card n n Website can be spoofed. Works for individuals, requires recipient to type in several lines of gibberish correctly. From a trusted source n Going back and back: Where does the trust stem from?

Use of Asymmetric Cryptography n n Notations: n E – public key, D – secret key n EC (M) – encryption of M using key C. n DC(M) – decryption of M using key C. Asymmetric cryptography key identities n DEED(M) = M n DDEE(M) = M

Use of Asymmetric Cryptography n Secret Transmission of messages n n Alice uses public key of Bob to encrypt her messages to him: EE(Bob)(M). Bob uses his private key to decrypt the message: DD(Bob)EE(Bob)(M).

Use of Asymmetric Cryptography n Signing a message I: n n n Alice encrypts the message with her private key: ED(Alice)(M). Bob decrypts with her public key and obtains M = DE(Alice) ED(Alice)(M). If M makes sense, Bob knows that someone with Alice secret key send the message.

Use of Asymmetric Cryptography n Signing a message II n This method avoids encryption of the whole message. n n Alice uses a MAC of her message: MAC(M). She sends Bob M and ED(Alice)(MAC(M)). Bob calculates n n n Asymmetric cryptography is very compute intensive. MAC(M) = DE(Alice) (ED(Alice)(MAC(M))). Bob verifies that this is the correct MAC. Bob concludes that the message was sent by someone knowing Alice’s private key.

Key Management n Generic Rules: n n n Use symmetric cryptography as much as possible for performance. Never use keys more than once. Key Management becomes an issue.

Key Management n Keys have limited lifetimes: n Cryptanalysis is easier with more material. n n Breaking WEP involves harvesting a large number of packets. Once found, a compromised key continues to do damage.

Key Management n Key Management Life Cycles: n Key establishment n n n Key generation Key distribution Key backup / recovery, key escrow Key replacement / update (rekeying) Key revocation Key expiration / Key termination / Key destruction

Key Management n Key generation n Uses random number generation n n Pseudo-random generation derived from a seed WEP: seed based on user key word. Not as random as appeared. Hardware random number generation Combined methods

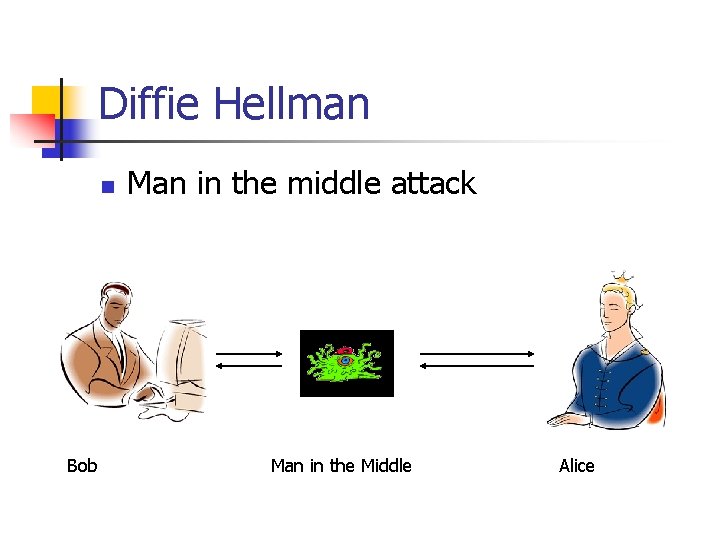
Key Management n Key distribution n n Has issues of authentication and confidentiality. Diffie-Hellman protocol solves confidentiality: n n Allows two parties to agree on a common secret. Subject to the man-in-the-middle attack n n n Alice thinks that she shares a secret with Bob. In reality, she communicates with M, and shares the secret with him. M shares another secret with Bob.

Key Management n Key backup / recovery n Accidental loss of key n n Control of encrypted information n n hardware failure, forgotten password … Employer cannot entrust enterprise-critical data to complete control of a single / group of employees. Key escrow n To preserve possibility of access by law enforcement agencies. n n In the UK, it is a crime to withhold a key to encrypted data under subpoena. In the US, such a law is seen to contradict 5 th amendment protection.

Key Management n Key destruction n Secure key destruction is far easier than secure file erasure. Key destruction destroys accessibility to encrypted data. Key archiving n Necessary for validation of old signatures, of integrity of old messages, …

Key Management n Symmetric key transport: n n Send symmetric key along, protected by public key of recipient. Saves on processing time

Diffie-Hellman n n Uses calculation modulo p, p a large prime. Chooses generator g. n n n Ideally, gx, x = 0, …, p -2 runs through all numbers 1, … p -1. Uses the fact that calculating powers gx is computationally feasible. But discrete logarithm (given gx find x) is not.

Diffie Hellman n n n Alice generates random number a mod p. Bob generates random number b mod p. Alice sends Bob ga mod p. Bob sends Alice gb mod p. Alice calculates (gb)a mod p. Bob calculates (ga)b mod p. These numbers are identical and the shared key.

Diffie Hellman n Bob Man in the middle attack Man in the Middle Alice

Diffie Hellman n Alice sends Bob ga mod p. n n Bob sends Alice gb mod p. n n But message goes to alien. Alien sends Bob gc mod p. But message goes to alien. Alien sends Alice gd mod p. Alice calculates (gd)a mod p. Bob calculates (gc)b mod p. These set up a secure communication channel between the alien and Bob and one between the alien and Alice.

Diffie Hellman n n Secure against eavesdroppers. Can be secured against man-in-themiddle by using authenticated gb mod p or by using a published value gb mod p.

Diffie Hellman and all other schemes n The problem is one of authentication and trust.