COE 561 Digital System Design Synthesis Sequential Logic

COE 561 Digital System Design & Synthesis Sequential Logic Synthesis Dr. Aiman H. El-Maleh Computer Engineering Department King Fahd University of Petroleum & Minerals

Outline n Modeling synchronous circuits n State-based optimization methods • State-based models. • Structural models. • State minimization. • State encoding for two-level logic • Input encoding • Output encoding • State encoding for multiple-level logic n Structural-based optimization methods • Retiming 2

Synchronous Logic Circuits n Interconnection of • Combinational logic gates. • Synchronous delay elements • E-T or M-S registers. n Assumptions • No direct combinational feedback. • Single-phase clocking. 3

Modeling Synchronous Circuits n State-based model • Model circuits as finite-state machines. • Represented by state tables/diagrams. • Lacks a direct relation between state manipulation and • corresponding area and delay variations. Apply exact/heuristic algorithms for • State minimization. • State encoding. n Structural models • Represent circuit by synchronous logic network. • Apply • Retiming. • Logic transformations. 4

State-Based Optimization 5

Formal Finite-State Machine Model n Defined by the quintuple ( , , S, , ). n A set of primary inputs patterns . n A set of primary outputs patterns . n A set of states S. n A state transition function n An output function • : S S. • : S for Mealy models • : S for Moore models. 6

State Minimization n Aims at reducing the number of machine states n State reduction may reduce n Completely specified finite-state machines n Incompletely specified finite-state machines • reduces the size of transition table. • the number of storage elements. • the combinational logic due to reduction in transitions • No don't care conditions. • Easy to solve. • Unspecified transitions and/or outputs. • Intractable problem. 7

State Minimization for Completely-Specified FSMs n Equivalent states • Given any input sequence the corresponding output sequences match. n Theorem: Two states are equivalent iff n Equivalence is transitive • they lead to identical outputs and • their next-states are equivalent. • Partition states into equivalence classes. • Minimum finite-state machine is unique. 8

Algorithm n Stepwise partition refinement. n Initially • 1 = States belong to the same block when outputs are the same for any input. n Refine partition blocks: While further splitting is possible • k+1 = States belong to the same block if they were previously in the same block and their next-states are in the same block of k for any input. n At convergence • Blocks identify equivalent states. 9

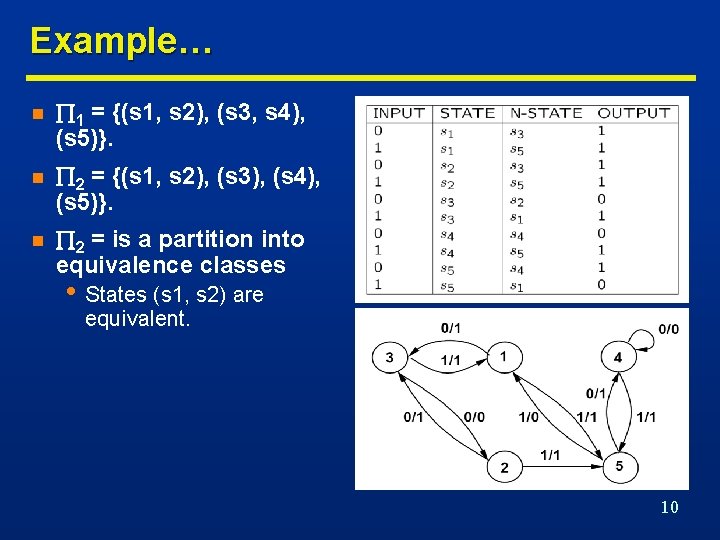
Example… n 1 = {(s 1, s 2), (s 3, s 4), (s 5)}. n 2 = {(s 1, s 2), (s 3), (s 4), (s 5)}. n 2 = is a partition into equivalence classes • States (s 1, s 2) are equivalent. 10

…Example… Original FSM Minimal FSM 11

…Example Original FSM {OUT_0} = IN_0 Latch. Out_v 1' + IN_0 Latch. Out_v 3' + IN_0' Latch. Out_v 2' v 4. 0 = IN_0 Latch. Out_v 1' + Latch. Out_v 1' Latch. Out_v 2' v 4. 1 = IN_0' Latch. Out_v 2 Latch. Out_v 3 + IN_0' Latch. Out_v 2' v 4. 2 = IN_0 Latch. Out_v 1' + IN_0' Latch. Out_v 1 + IN_0' Latch. Out_v 2 Latch. Out_v 3 sis> print_stats pi= 1 po= 1 nodes= 4 latches= 3 lits(sop)= 22 #states(STG)= 5 Minimal FSM {OUT_0} = IN_0 Latch. Out_v 1' + IN_0 Latch. Out_v 2 + IN_0' Latch. Out_v 2' v 3. 0 = IN_0 Latch. Out_v 1' + Latch. Out_v 1' Latch. Out_v 2‘ v 3. 1 = IN_0' Latch. Out_v 1' + IN_0' Latch. Out_v 2' sis> print_stats pi= 1 po= 1 nodes= 3 latches= 2 lits(sop)= 14 #states(STG)= 4 12

Computational Complexity n Polynomially-bound algorithm. n There can be at most |S| partition refinements. n Each refinement requires considering each state n Actual time may depend upon • Complexity O(|S|2). • Data-structures. • Implementation details. 13

State Minimization for Incompletely-Specified FSMs … n Applicable input sequences n Compatible states • All transitions are specified. • Does not lead to any unspecified transition. • Given any applicable input sequence the corresponding output sequences match. n Theorem: Two states are compatible iff n Compatibility is not an equivalency relation (not transitive). • they lead to identical outputs (when both are specified), • their next-states are compatible (when both are specified). 14

… State Minimization for Incompletely Specified FSMs n Minimum finite-state machine is not unique. n Implication relations make problem intractable. n Example • Replace * by 1. • {(s 1, s 2), (s 3), (s 4), (s 5)}. • Replace * by 0. • {(s 1, s 5), (s 2, s 3, s 4)}. • Compatible states (s 1, s 2). • Incompatible states (s 1, s 3), (s 1, s 4), (s 2, s 5), (s 3, s 5), (s 4, s 5). • If (s 3, s 4) are compatible • then (s 1, s 5) are compatible. 15

Compatibility and Implications… n Compatible pairs n Incompatible pairs • (s 1, s 2) • (s 1, s 5) (s 3, s 4) • (s 2, s 4) (s 3, s 4) • (s 2, s 3) (s 1, s 5) • (s 3, s 4) (s 2, s 4) and (s 1, s 5) • (s 2, s 5), (s 3, s 5) • (s 1, s 4), (s 4, s 5) • (s 1, s 3) 16

…Compatibility and Implications n A class of compatible states is such that all state pairs are compatible. n A class is maximal n Closure property • If not subset of another class. • A set of classes such that all compatibility implications are satisfied. n The set of maximal compatibility classes n Minimum covers may involve compatibility classes that are not necessarily maximal. • Satisfies always the closure property. • May not provide a minimum solution. 17

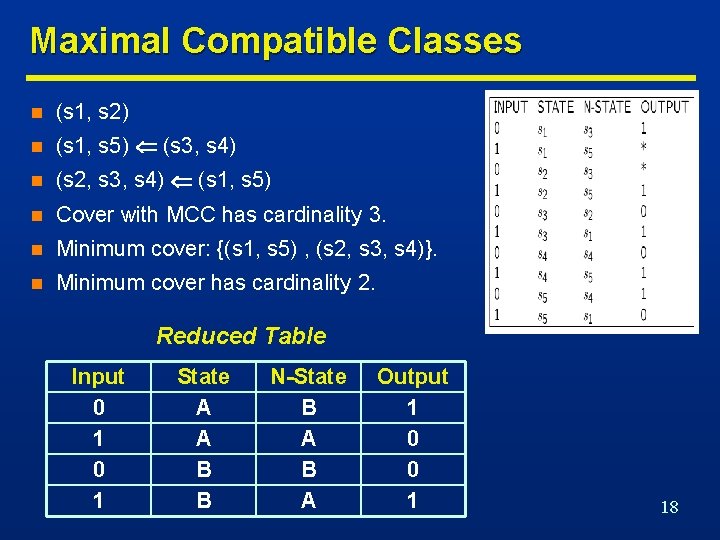
Maximal Compatible Classes n (s 1, s 2) n (s 1, s 5) (s 3, s 4) n (s 2, s 3, s 4) (s 1, s 5) n Cover with MCC has cardinality 3. n Minimum cover: {(s 1, s 5) , (s 2, s 3, s 4)}. n Minimum cover has cardinality 2. Reduced Table Input 0 1 State A A B B N-State B A Output 1 0 0 1 18

Finding Maximal Compatible Classes … n n n n Knowing that si and sj are two incompatible states implies that no maximal compatible class will contain both si and sj. Every set of states that does not contain any incompatible pair is a compatible set. Associate a variable xi to state si such that xi =1 implies that si is an element of the set. Write a conjunction of two-literal calluses. Each clause corresponds to an incompatible pair. Convert the expression into a prime and irredundant sum-of-product form. Every term corresponds to a maximal compatible set and represents the sets that do no appear in the prime implicant. 19

… Finding Maximal Compatible Classes n Example • Incompatible pairs • (s 2, s 5), (s 3, s 5) • (s 1, s 4), (s 4, s 5) • (s 1, s 3) • Two-literal Clauses • (x 2’+x 5’) (x 3’+x 5’) (x 4’+x 5’) (x 1’+x 4’) (x 1’+x 3’) • Prime and Irredundant sum-of-product • = (x 2’ x 3’ x 4’+x 5’) (x 1’+ x 3’x 4’) • = x 1’ x 2’ x 3’ x 4’+ x 1’x 5’+ x 2’ x 3’ x 4’+ x 3’x 4’ x 5’ • = x 1’x 5’+ x 2’ x 3’ x 4’+ x 3’x 4’ x 5’ • Maximal Compatible Classes • x 1’x 5’ → (S 2, S 3, S 4) • x 2’ x 3’ x 4’→ (S 1, S 5) • x 3’x 4’ x 5’ → (S 1, S 2) 20

Formulation of the State Minimization Problem n A class is prime, if not subset of another class implying the same set or a subset of classes. n Compute the prime compatibility classes. n Select a minimum number of PCC such that n Binate covering problem. n Upper bound on optimum solution given by n Lower bound on optimum solution given by • all states are covered. • all implications are satisfied. • Cardinality of set of maximal compatible classes and • Original state set cardinality. • A unate cover solution that disregards implications. 21

Setting Up Covering Problem… n All states must be contained in at least one compatible class (covering). n All compatible classes implied by any compatible class must be contained in a compatible class in the solution (closure). n Associate a variable ci to the i-th compatible class such that ci =1 implies that class i is part of the solution. n We write a Boolean formula (product of sum frm) to express the conditions for a set of compatible classes to represent a closed cover. • Terms representing covering constraints • Terms representing closure constraints. 22

…Setting Up Covering Problem… n Maximal compatibles classes n Covering constraints n Closure constraints • c 1: (s 1, s 2) • c 2: (s 1, s 5) (s 3, s 4) • c 3: (s 2, s 3, s 4) (s 1, s 5) • s 1: (c 1 + c 2) • s 2: (c 1 + c 3) • s 3: (c 3) • s 4: (c 3) • s 5: (c 2) • c 2 → c 3 : (c 2’ + c 3) • c 3 → c 2 : (c 3’ + c 2) 23

…Setting Up Covering Problem n Binate covering problem n Minimum cover: {c 2 c 3}. n Minimum cover: {(s 1, s 5) , (s 2, s 3, s 4)}. • (c 1 + c 2) (c 1 + c 3) (c 2) (c 3) (c 2’ + c 3) (c 3’ + c 2) • =(c 1 + c 2 c 3) (c 2) (c 3) (c 2’ + c 3) (c 3’ + c 2) • = (c 2 c 3) 24

Finding Prime Compatible Classes… n n All maximal compatible classes are prime. Let C 1 and C 2 be two compatible classes such that C 1 C 2. • One tempted to favor C 1 over C 2 as it covers more states. • It might be better to choose C 2 in case that C 1 implies the selection of other compatible classes that would not be required if C 2 is selected. n n n The set of compatible classes implied by a compatible class is denoted as its class set (CS). For each maximal compatible class p of size k with a non-empty class set, consider all its subsets Sp of compatible classes of size k-1. For each s Sp, and for all primes q of size > k-1, if s q and CSs CSq then s is not prime. Otherwise, it is prime. 25

…Finding Prime Compatible Classes n Maximal compatibles classes n Prime compatibles classes • (s 1, s 2) • (s 1, s 5) (s 3, s 4) • (s 2, s 3, s 4) (s 1, s 5) • (s 2, s 3, s 4) • (s 2, s 3) (s 1, s 5) Not prime • (s 2, s 4) (s 3, s 4) Prime • (s 3, s 4) (s 2, s 4) and (s 1, s 5) Not prime • (s 1, s 5) • (s 1) Not prime • (s 5) Prime n Set of prime compatible classes • (s 1, s 2), (s 1, s 5), (s 2, s 3, s 4), (s 2, s 4), (s 5) 26

An Interesting Example n Moore machine with 3 -states. n Replace don’t care output of s 1 by 0 → Can’t be minimized. n n Inpu Stat t e 0 Replace don’t care output of s 2 by 1 1 → Can’t be minimized. 0 Maximal compatible classes 1 • (s 1, s 2) (s 1, s 3) 0 • (s 1, s 3) (s 1, s 2) 1 Input Machine can be reduced to two states. 0 Replacing don’t cares with all 1 possible assignments does not guarantee a minimum solution. 0 1 NOut Stat e s 1 s 2 s 1 s 3 s 2 0 s 2 s 1 0 s 3 s 1 1 s 3 1 State NOut State A A 0 A B 0 B A 1 B B 1 27

State Encoding n Determine a binary encoding of the states (|S|=ns) that optimize machine implementation • • area. cycle-time. n Assume D-type registers. n Circuit complexity is related to • • Number of storage bits nb used for state representation Size of combinational component n There are n Modeling • • possible encodings Two-level circuits. Multiple-level circuits. 28

Two-Level Circuit Models n Sum of product representation. • PLA implementation. n Area n Delay • # of products (rows) # I/Os (columns). • Twice # of products (2 column length) plus # I/Os (1 row length). n Note • # products of a minimum implementation. • # I/Os depends on encoding length. 29

State Encoding for Two-Level Models n Early work focused on use of minimum-length codes i. e. using nb= log 2 ns. n Most classical heuristics are based on reduced dependency criterion • Encode states so that state variables have least • n dependencies on those representing previous states Correlates weakly with minimality of sum-of-products representation Symbolic minimization of state table. • Equivalent to minimizing the size of sum-of-products form related to all codes that satisfy the corresponding constraints n Constrained encoding problems. • Exact and heuristic methods. 30

Symbolic Minimization n n n Minimization of Boolean functions where codes of inputs and/or outputs are not specified. Minimize tables of symbols rather than binary tables. Extension to bvi and mvi function minimization. Reduce the number of rows of a table, that can have symbolic fields. Reduction exploits • Combination of input symbols in the same field. • Covering of output symbols. Applications • Encoding of op-codes. • State encoding of finite-state machines Problems: • Input encoding. • Output encoding. • Mixed encoding. 31

Input Encoding Example Replace symbols by binary strings to minimize corresponding covers 32

Definitions n Symbolic cover n Symbolic implicant n Symbolic literals • List of symbolic implicants. • List of rows of a table. • Conjunction of symbolic literals. • Simple: one symbol. • Compound: the disjunction of some symbols. 33

Input Encoding Problem n Degrees of freedom in encoding the symbols. n Goal n Approach • Reduce size of the representation. • Encode to minimize number of rows. • Encode to minimize number of bits. n Represent each string by 1 -hot codes. n Table with positional cube notation. n Minimize table with mvi minimizer. n Interpret minimized table • Compound mvi-literals. • Groups of symbols. 34

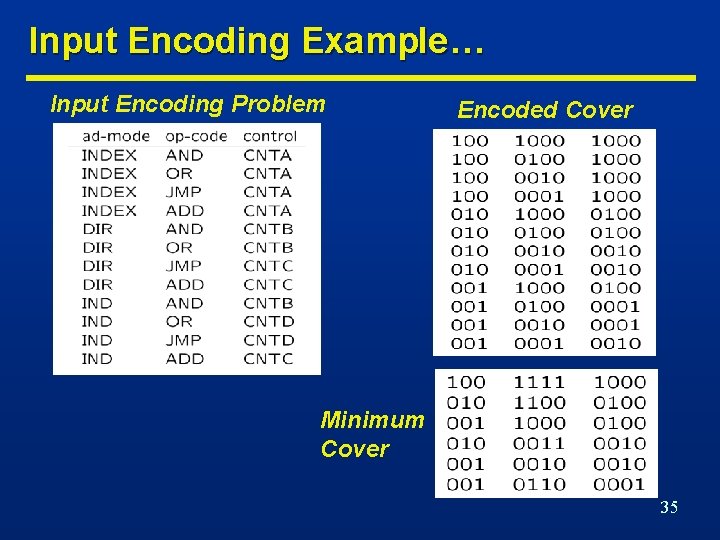
Input Encoding Example… Input Encoding Problem Encoded Cover Minimum Cover 35

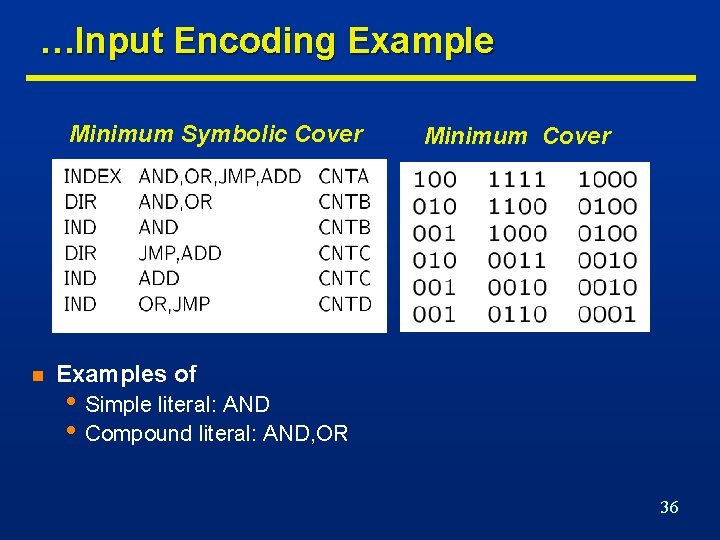
…Input Encoding Example Minimum Symbolic Cover n Minimum Cover Examples of • Simple literal: AND • Compound literal: AND, OR 36

Input Encoding Problem n Transform minimum symbolic cover into minimum bvcover. n Map symbolic implicants into bv implicants (one to one). n Compound literals • Encode corresponding symbols so that their supercube does not include other symbol codes. n Replace encoded literals into cover. 37

Example n Compound literals n Valid code • AND, OR, JMP, ADD • AND, OR • JMP, ADD • OR, JMP • {AND 00, OR 01, JMP 11, ADD 10} Replacement in cover Invalid code 38

Input Encoding Algorithms n Problem specification n Solution sought for • Constraint matrix A • aij = 1 iff symbol j belongs to literal i. • Encoding matrix E • As many rows as the symbols. • Encoding length nb. n Constraint matrix n Encoding matrix 39

Input Encoding Problem n Given constraint matrix A • Find encoding matrix E • satisfying all input encoding constraints (due to compound literals) • With minimum number of columns (bits). n An encoding matrix E satisfies the encoding constrains by A if for each row a. T of A • The supercube of rows of E corresponding to 1’s in a. T does not intersect any of the rows of E corresponding to 0’s in a. T. n Identity matrix is always a valid encoding. n Theorem: Given a constraint matrix A, the encoding matrix E=AT satisfies the constrains of A. • 1 -hot encoding 40

Dichotomy Theory n Dichotomy n Encoding n • Two sets (L, R). • Bipartition of a subset of the symbol set. • Set of columns of E. • Each column corresponds to a bipartition of symbol set. Rationale • Encoding matrix is equivalent to a set of bipartitions. • Each row of the constraint matrix implies some choice on the codes i. e. induces a bipartition. 41

Dichotomies n Dichotomy associated with row a. T of A • A set pair (L, R) • L has the symbols with the 1 s in a. T • R has the symbols with the 0 s in a. T n Seed dichotomy associated with row a. T of A • A set pair (L, R) • L has the symbols with the 1 s in a. T • R has one symbol with a 0 in a. T n n Dichotomy associated with constraint a. T = 1100 • ({AND, OR}; {JMP, ADD}). The corresponding seed dichotomies are • ({AND, OR}; {JMP}) • ({AND, OR}; {ADD}). 42

Definitions n Compatibility • (L 1, R 1) and (L 2, R 2) are compatible if • L 1 R 2 = and R 1 L 2 = or • L 1 L 2 = and R 1 R 2 = . n Covering • Dichotomy (L 1, R 1) covers (L 2, R 2) if • L 1 L 2 and R 1 R 2 or • L 1 R 2 and R 1 L 2. n Prime dichotomy • Dichotomy that is not covered by any compatible dichotomy of a given set. n Union of two compatible dichotomies is a dichotomy covering both with smallest left and right blocks. 43

Exact Input Encoding n Compute all prime dichotomies. n Form a prime/seed dichotomy table. n Find minimum cover of seeds by primes. n An encoding can be found based on n Prime dichotomies can be computed based on Compatibility graphs of seed dichotomies by • Compatibility graphs of seed dichotomies by a clique covering • Conflict graphs of seed dichotomies by a graph coloring • Finding largest clique covering each edge 44

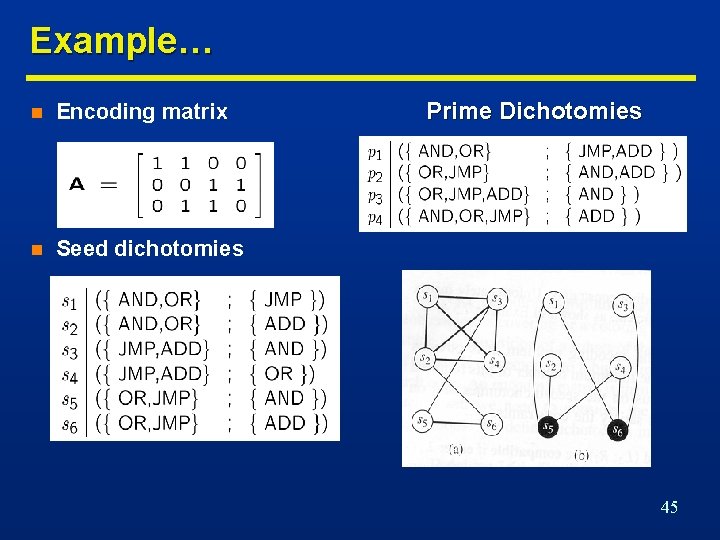
Example… n Encoding matrix n Seed dichotomies Prime Dichotomies 45

…Example n Table n Minimum cover: p 1 and p 2 n Encoding 46

Heuristic Encoding n Determine dichotomies of rows of A. n Column-based encoding n • Construct E column by column. Iterate • • • Determine maximum compatible set. Find a compatible encoding. Use it as column of E. n Dichotomies n First two dichotomies are compatible. n Encoding column [1100]T satisfies d 1 , d 2. n Need to satisfy d 3. Second encoding column [0110]T. 47

Output and Mixed Encoding n Output encoding n Mixed encoding • Determine encoding of output symbols. • Determine both input and output encoding • Examples • Interconnected circuits. • Circuits with feedback. 48

Symbolic Minimization n n n Extension to mvi-minimization. Accounts for • Covering relations. • Disjunctive relations. Exact and heuristic minimizers. Minimum symbolic cover computed before Can we use fewer implicants? Can we merge implicants? 49

Covering Relations Example n Assume the code of CNTD covers the codes of CNTB and CNTC. n Possible codes • CNTA = 00, CNTB = 01, • CNTC =10 and CNTD = 11. 50

Disjunctive Relations Example n Assume the code of CNTD is the OR of the codes of CNTB and CNTC. n Possible codes • CNTA = 00, CNTB = 01, • CNTC =10 and CNTD = 11. 51

Output Encoding Algorithms n Often solved in conjunction with input encoding. Exact algorithms n Heuristic algorithms n Compatibility n • Prime dichotomies compatible with output constraints. • Construct prime/seed table. • Solve covering problem. • Construct E column by column. • (L 1, R 1) and (L 2, R 2) are compatible if L 1 R 2 = and R 1 L 2 = n Covering n Prime dichotomies need to cover at least one element of all seed pairs. • Dichotomy (L 1, R 1) covers (L 2, R 2) if L 1 L 2 and R 1 R 2 52

Example… n Input constraint matrix of second stage n Output constraint matrix of first stage n Assume the code of CNTD covers the codes of CNTB and CNTC. 53

…Example… n Seed dichotomies associated with A S 1 A: S 1 B: S 2 A: S 2 B: S 3 A: S 3 B: S 4 A: S 4 B: n ( {CNTA, CNTB} ; {CNTC} ) ( {CNTC} ; {CNTA, CNTB} ) ( {CNTA, CNTB} ; {CNTD} ) ( {CNTD} ; {CNTA, CNTB} ) ( {CNTB, CNTD} ; {CNTA} ) ( {CNTA} ; {CNTB, CNTD} ) ( {CNTB, CNTD} ; {CNTC} ) ( {CNTC} ; {CNTB, CNTD} ) Seed dichotomies s 2 A, s 3 B and s 4 are not compatible with B bec. Encoding bit for CNTD is 0. 54

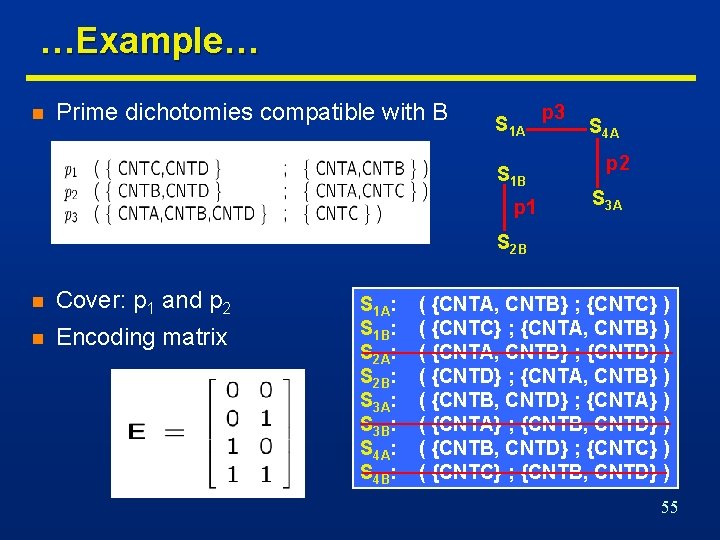
…Example… n Prime dichotomies compatible with B S 1 A S 1 B p 1 p 3 S 4 A p 2 S 3 A S 2 B n Cover: p 1 and p 2 n Encoding matrix S 1 A: S 1 B: S 2 A: S 2 B: S 3 A: S 3 B: S 4 A: S 4 B: ( {CNTA, CNTB} ; {CNTC} ) ( {CNTC} ; {CNTA, CNTB} ) ( {CNTA, CNTB} ; {CNTD} ) ( {CNTD} ; {CNTA, CNTB} ) ( {CNTB, CNTD} ; {CNTA} ) ( {CNTA} ; {CNTB, CNTD} ) ( {CNTB, CNTD} ; {CNTC} ) ( {CNTC} ; {CNTB, CNTD} ) 55

…Example n Heuristic encoding considers the dichotomy pairs associated with each row d 1 A: d 1 B: d 2 A: d 2 B: ( {CNTC, CNTD} ; {CNTA, CNTB} ) ( {CNTA, CNTB} ; {CNTC, CNTD} ) ( {CNTB, CNTD} ; {CNTA, CNTC} ) ( {CNTA, CNTC} ; {CNTB, CNTD} ) n Dichotomies d 1 B and d 2 B do not satisfy output constraints. n Dichotomies d 1 A and d 2 A are not compatible and considered one at a time yielding two-column encoding. 56

State Encoding of Finite-State Machines n Given a (minimum) state table of a finite-state machine • Find a consistent encoding of the states • that preserves the cover minimality • with minimum number of bits. n The state set must be encoded while satisfying simultaneously both input and output constraints 57

Example… Minimum Symbolic Covering Constraints • s 1 and s 2 cover s 3 • s 5 is covered by all other states. Encoding Constraint Matrices 58

…Example… After Implicant Merging: 0 1 2 3 4 5 6 s 1, s 2 1 s 3 0 s 4, s 5 s 1, s 4 0 s 3 1 s 5 s 3 s 1 0 1 s 4 1 0 s 5 s 2 s 3 If s 1 s 3 and s 1 s 3 : * 1 1 0 0 1 s 1, s 2, s 4 s 2 s 3 s 4, s 5 s 3 s 1 s 4 s 2 s 5 0 1 1 1 0 0 Last two rows, output is 0 => no impact on output equation. If s 5 is covered by all other states, a minimal code will have s 5 assigned the 0 code, i. e. no impact on next state equations => last two rows can be eliminated. * s 1, s 2, s 4 s 3 0 1 s 2 s 1 1 1 s 3 s 4 1 0 s 4, s 5 s 2 1 59

…Example n Encoding matrix (one row per state( Covering Constraints • s 1 and s 2 cover s 3 • s 5 is covered by all other states. n Encoded cover of combinational component 60

Limitation of Symbolic Minimization and Constrained Encoding n n The minimum-length solution compatible with a set of constraints may require bits larger than log 2 ns. Example: Consider an FSM whose minimal symblic cover is: • 00 • 01 • 10 s 1, s 2, s 3 s 1, s 3 100 s 1 010 s 2 001 n Satisfaction of input constraints requires at least 3 bits. n Assume we do not satisfy first input constraint • e. g. s 1=1000, s 2=010, s 3=001 • PLA size is 3 rows and 11 columns (2 PI+3 PS+3 NS+3 PO) • 2 bits are sufficient • PLA size is 4 rows and 9 columns (2 PI+2 PS+2 NS+3 PO) 61

State Encoding for Multiple-Level Models n Logic network representation. n Area: # of literals. n Delay: Critical path length. n Encoding based on cube-extraction heuristics [Mustang-Devadas]. n Rationale • When two (or more) states have a transition to the same nextstate • Keep the distance of their encoding short. • Extract a large common cube. n Exploit first stage of logic. n Works fine because most FSM logic is shallow. 62

Example n 5 -state FSM (3 -bits). n Encoding n Transition • s 1 s 3 with input i. • s 2 s 3 with input i’. • s 1 000 = a’b’c’. • s 2 001 = a’b’c. • i a’b’c’ +i’ a’b’c = a’b’ (ic+i’c’) • 6 literals instead of 8. 63

Algorithm n n Examine all state pairs • Complete graph with |V| = |S|. Add weight on edges • • Model desired code proximity. The higher the weight the lower the distance. Embed graph in the Boolean space. • Objective is to minimize the cost function Difficulties • • The number of occurrences of common factors depends on the next-state encoding. The extraction of common cubes interact with each other. 64

Mustang Algorithm Implementation… n Fanout-oriented algorithm • • • Consider state fanout i. e. next states and outputs. Assign closer codes to pair of states that have same next state transition or same output. Maximize the size of the most frequent common cubes. 65

… Mustang Algorithm Implementation … n Fanin-oriented algorithm • • • Consider state fan-in i. e. present states and inputs. Assign closer codes to pair of states that have transition from same present state or same input. Maximize the frequency of the largest common cubes. 66

…Mustang Algorithm Implementation 67

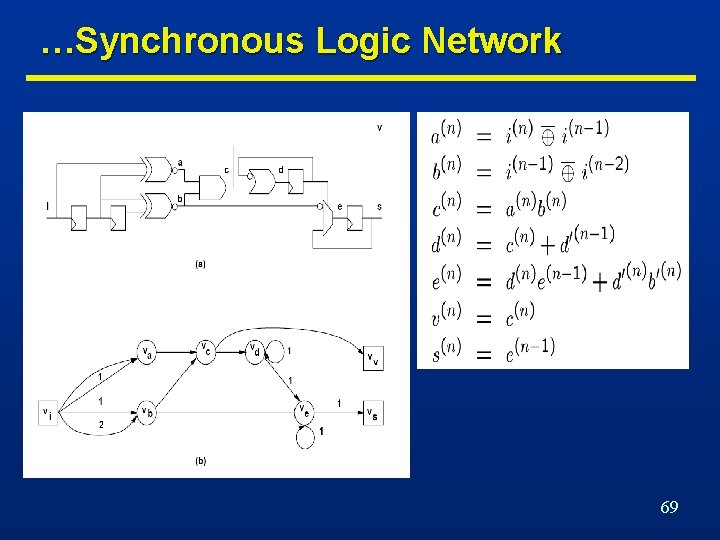
Synchronous Logic Network… n Synchronous Logic Network n Synchronous network graph: • Variables. • Boolean equations. • Synchronous delay annotation. • Vertices equations I/O , gates. • Edges dependencies nets. • Weights synch. delays registers. 68

…Synchronous Logic Network 69

Approaches to Synchronous Logic Optimization n Optimize combinational logic only. n Optimize register position only n Optimize overall circuit • Retiming. • Peripheral retiming. • Synchronous transformations • Algebraic. • Boolean. 70

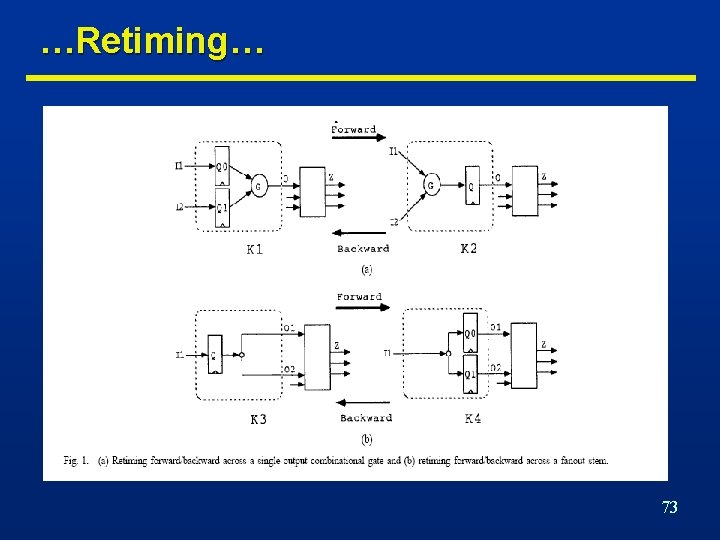
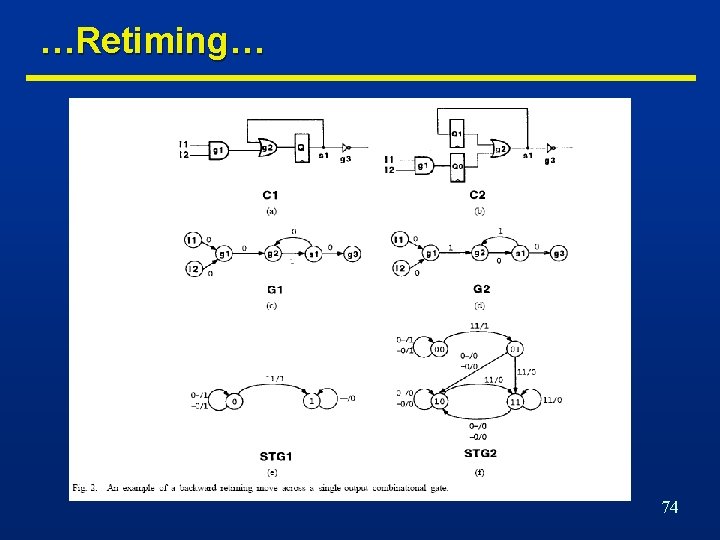
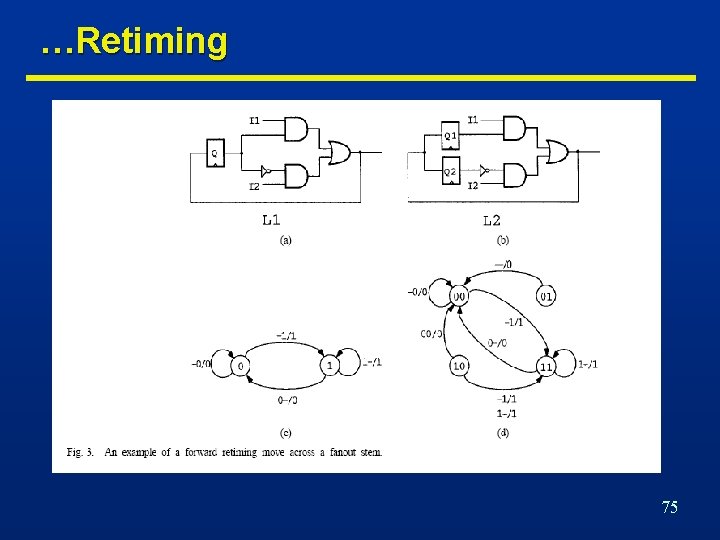
Retiming… n Minimize cycle-time or area by changing register positions. n Do not modify combinational logic. n Preserve network structure • Modify weights. • Do not modify graph structure. 71

…Retiming… n Global optimization technique [Leiserson]. n Changes register positions • affects area • changes register count. • affects cycle-time • changes path delays between register pairs. n Solvable in polynomial time. n Assumptions • Vertex delay is constant: No fanout delay dependency. • Graph topology is invariant: No logic transformations. • Synchronous implementation • Cycles have positive weights. • Edges have non-negative weights. 72

…Retiming… 73

…Retiming… 74

…Retiming 75

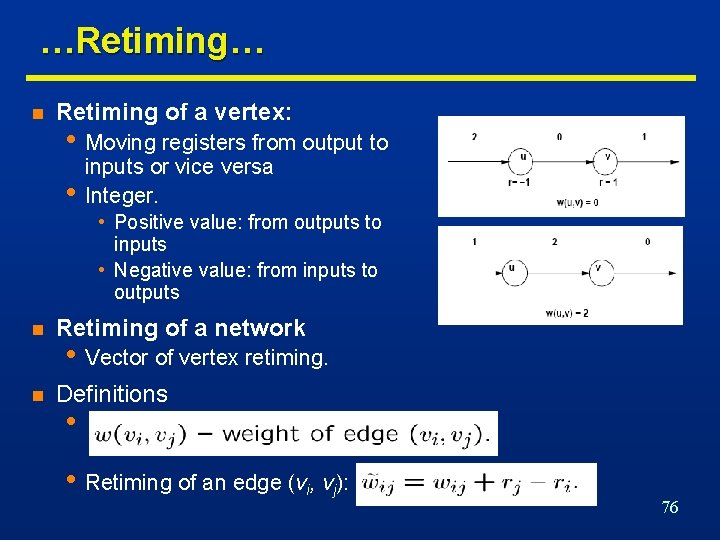
…Retiming… n Retiming of a vertex: • Moving registers from output to • inputs or vice versa Integer. • Positive value: from outputs to inputs • Negative value: from inputs to outputs n Retiming of a network n Definitions • Vector of vertex retiming. • • Retiming of an edge (vi, vj): 76

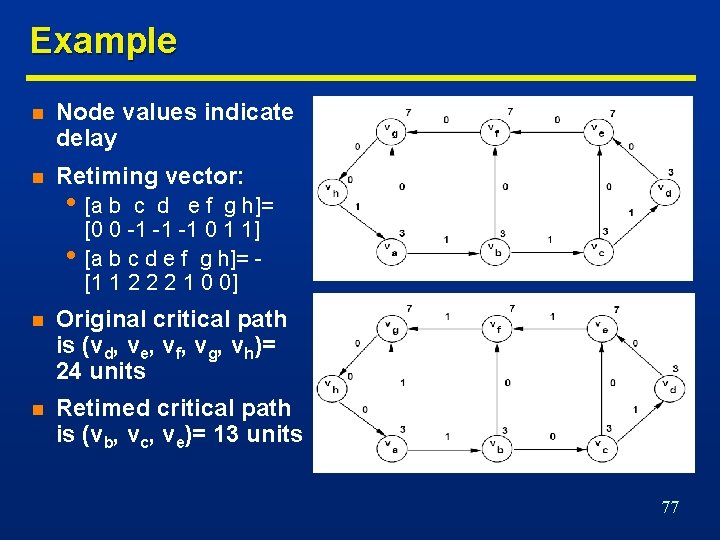
Example n Node values indicate delay n Retiming vector: • [a b • c d e f g h]= [0 0 -1 -1 -1 0 1 1] [a b c d e f g h]= [1 1 2 2 2 1 0 0] n Original critical path is (vd, ve, vf, vg, vh)= 24 units n Retimed critical path is (vb, vc, ve)= 13 units 77

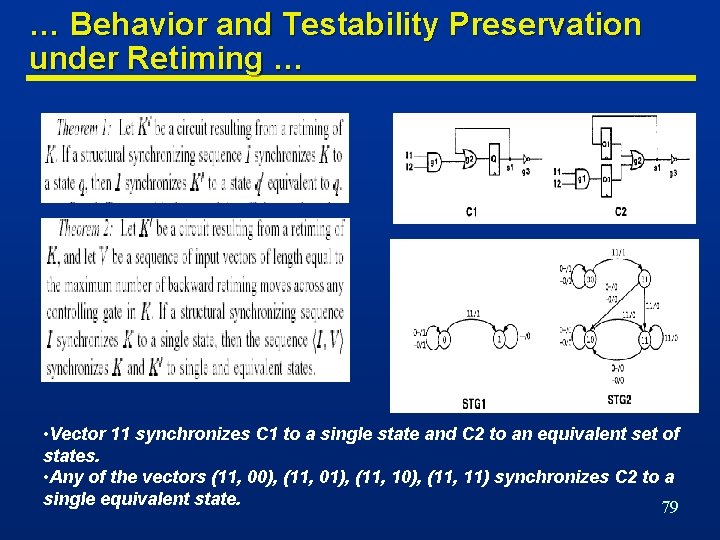
Behavior and Testability Preservation under Retiming … n A synchronizing sequence for a machine is an input sequence that brings the machine to a known and unique state determined without knowledge of output response or initial state of the machine. n An interesting class of synchronizing sequences allows the state reached after applying the synchronizing sequence to be either a single state or a set of equivalent states. n A synchronizing sequence (or a test) derived based on pessimistic 3 -valued simulation is called structural; otherwise, it is called functional. • functional synchronizing sequences (or tests) correspond to those derived based on the state transition graph of a circuit. 78

… Behavior and Testability Preservation under Retiming … • Vector 11 synchronizes C 1 to a single state and C 2 to an equivalent set of states. • Any of the vectors (11, 00), (11, 01), (11, 10), (11, 11) synchronizes C 2 to a single equivalent state. 79

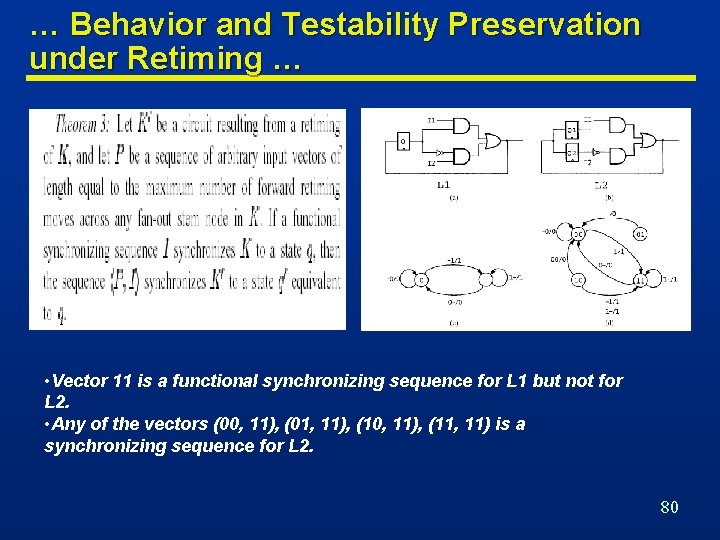
… Behavior and Testability Preservation under Retiming … • Vector 11 is a functional synchronizing sequence for L 1 but not for L 2. • Any of the vectors (00, 11), (01, 11), (10, 11), (11, 11) is a synchronizing sequence for L 2. 80

… Behavior and Testability Preservation under Retiming 81