COE 360 Principles of VLSI Design Conduction in

COE 360 Principles of VLSI Design Conduction in Semiconductors

Previous Lecture • • • Insulators, Semiconductors, and Conductors Semiconductors: Ge, Si, Ga. As, Si. C Si has 14 electrons: 2 , 8, 4 (Grop-4) At 0 ºK, silicon is an insulator As temperature increases, more bonds are broken creating more free electrons and more free holes. Carrier concentration = #/cm 3 Intrinsic semiconductor = pure semiconductor Extrinsic = impure or doped Mass Action Law np = ni 2 2

Previous Lecture • Intrinsic semiconductor + trivalent impurity (Group-3) p-type semiconductor. • Majority holes p ≈ NA (Acceptor) • Minority electrons n = ni 2 / NA • Intrinsic semiconductor + pentavalent impurity (Group-5) n -type semiconductor. • Majority electrons n ≈ ND (Donor) • Minority holes p = ni 2 / ND 3

Group Activity 4

Conduction in Semiconductors Conduction is carried out by means of 1. Drift Process. 2. Diffusion Process. 5

Current in Semiconductors • The two processes that cause free electrons and holes to move in a semiconductor are drift and diffusion. • Drift – the movement of holes and electrons due to an electric field • Diffusion – the movement of holes and electrons due to variations in concentrations. 6

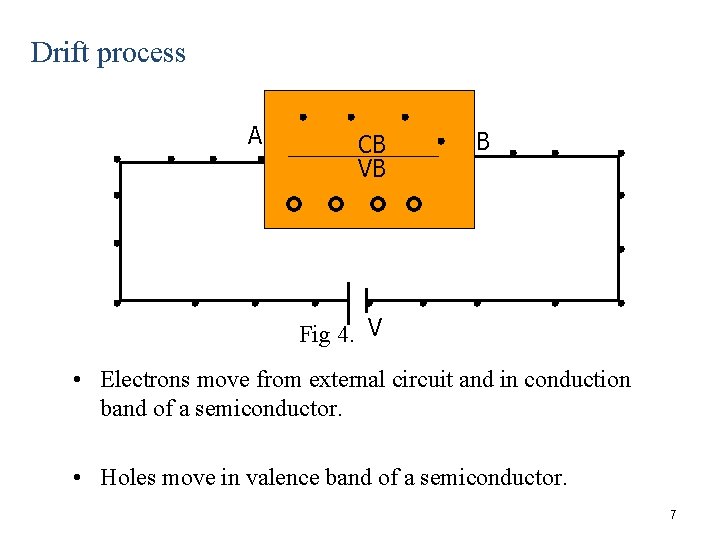
Drift process A CB VB B Fig 4. V • Electrons move from external circuit and in conduction band of a semiconductor. • Holes move in valence band of a semiconductor. 7

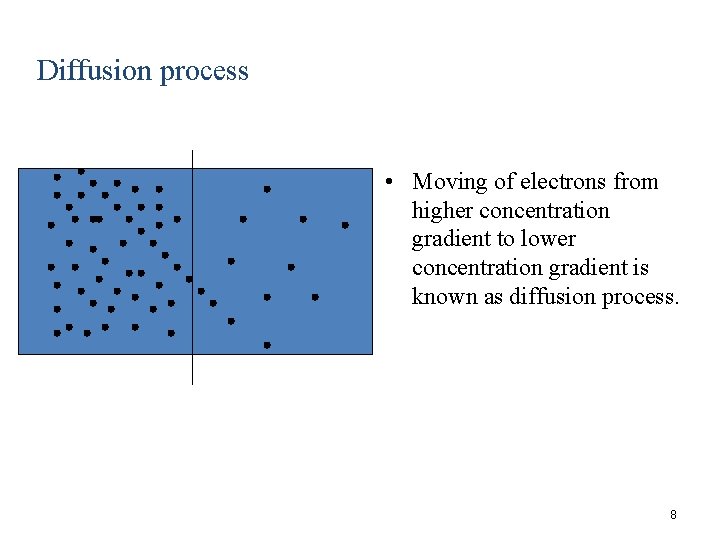
Diffusion process • Moving of electrons from higher concentration gradient to lower concentration gradient is known as diffusion process. 8

Current Density and Conductivity • Current density (J) is the current per unit area in the conducting medium J=I/A A/m 2 – J = current density in amperes/m 2 – I = current through a conductor, in amperes – A = cross-sectional area of the conductor, m 2 9

Example 1) A current of 6 m. A is flowing through a copper wire that has an area of 4 mm 2. What is the current density? • Answer: The current through the conductor is I = 6 m. A = 0. 006 amperes (or 6 x 10 -3 amps). • The area of the wire is A = 4 mm 2 = 0. 004 m 2 (or 4 x 10 -3 m 2). Use the equation for current density. J = I/A J = 0. 006 amps/0. 004 m 2 J = 1. 5 amps/m 2 10

Example • If 45 amperes of current is flowing through a battery with a given area of 8 m 2, what is the current density? • Answer: The current, I = 45 amps and the area A = 8 m 2. J = I/A J = 45 amps/8 m 2 J = 5. 63 amps/m 2 11

Current Density and Conductivity J=I/A A/m 2 J=qnμƐ=σƐ A/m 2 • Conductivity of the material σ=qnμ (Ω. m)-1 q : magnitude of electronic charge n : electron concentration , μ : mobility , Ɛ : electric field (Epsilon). σ : electric conductivity (Sigma) V = Ɛ L 12

Resistance, Resistivity Resistance, R Resistivity, : surface area of current flow path length The electrical conductivity σ = 1/

Conductivity and Resistivity • In a semiconductor, both electrons and holes conduct current: • The conductivity of a semiconductor is – Unit: mho/cm • The resistivity of a semiconductor is – Unit: ohm-cm (J) : Current density

Example What is the resistivity of a Si sample doped with 1016/cm 3 Boron (Group-3)? Assume μn=1500 cm 2/V. s, μp=450 cm 2/V. s, Answer:

Group Activity 16

Example • An N-type piece of Si has 1015 cm-3 donors concentration. Acceptors are added at a concentration of 1016 cm-3. What is the type of the resulting material and its resistance? 17

Example • An N-type piece of Si has 1015 cm-3 donors concentration. Acceptors are added at a concentration of 1016 cm-3. What is the type of the resulting material and its resistance? • NA >>ND ------ P-type • P = NA – ND = 1016 - 1015 • σ = 0. 684 = 1. 54 • R= 1. 54 x 104 = 15. 40 K 18

Example • P-type Si has a Resistivity of 1Ω. cm. What is the required donors concentration to invert it i. e ( make it n-type ) while keeping Resistivity the same ? • Assume μn=600 cm 2/V. s, μp=250 cm 2/V. s 19

Answer for p-type ignore electron conductivity for n-type ignore hole conductivity 20

Example • An n-type silicon sample is 3 mm long and has a rectangular cross section 50*100 μm. The donor concentration at 300 K is 5*1014 cm-3. A steady current of 1μA exists in the bar. Determine a)electron concentration b)hole concentration c)conductivity d)voltage across the bar Assume ni=1. 45*1010 cm-3, μn=1500 cm 2/V. s 21

Solution • 22

Example A conducting line on an IC chip is 2. 8 mm long and has a rectangular cross section 1*4μm. A current of 5 m. A produces a voltage drop of 100 m. V across the line. Determine electron concentration given that the electron mobility is 500 (cm 2/V. s) Solution R=V/I = 100/5 = 20 R= L/A = R A/L =( 20 *1*10 -6*4*10 -6)/(2. 8*10 -3) σ=1 / =3. 5*10 7(Ω. m) -1 σ = nqμ n=σ/(qμ)=3. 5*107/(1. 6*10 -19*500*10 -4)=4. 38*1027 m-3 = 4. 38*1021 cm-3 23