Code parameters optimization DTL Tank 1 error studies

Code parameters optimization & DTL Tank 1 error studies Maud Baylac, Emmanuel Froidefond Presented by JM De Conto LPSC-Grenoble HIPPI yearly meeting, Oxford, September, 2005

Overview • Goal, recall TW inputs • Optimization of code parameters • Nb runs • Nb calculations per βλ • Nb particles • Space charge routine: • 2 d vs 3 d • Mesh size • Error study • Individual sensitivity: longitudinal & transverse • Effect of input distribution • Global errors, loss • Set of tolerances

Goal • For us: learn how to use Trace. Win • Study sensitivity of DTL to quadrupole and field errors • Determine set of tolerances for tank 1 for quadrupole alignment quadrupole gradient klystron field amplitude and phase gap field amplitude

Trace. Win inputs • • • Several inputs: evolutive DTL design Input distribution: mainly type -32 (Gaussian) file Worse case scenario & Same for all studies 2 types of simulations: Sensitivity: one type of error at a time (e. g. : δx ) Global error effect: all types of errors at once Each error generated randomly & uniformly in [–max; +max] For all cases, transport to the end of the DTL

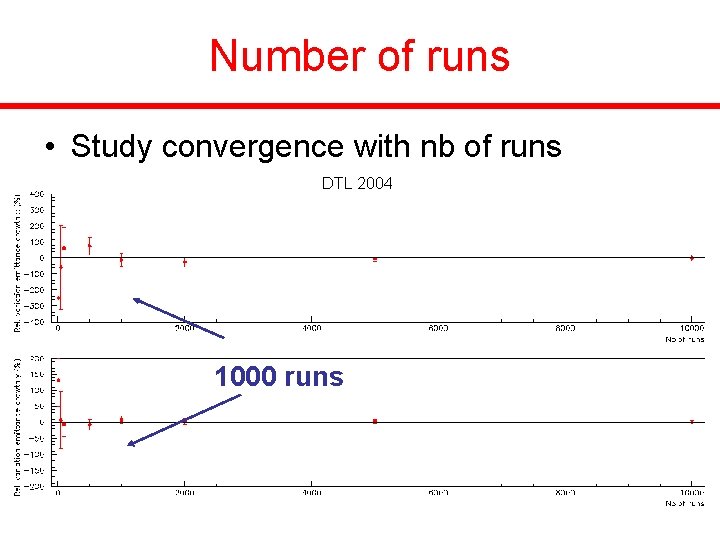
Number of runs • Study convergence with nb of runs DTL 2004 1000 runs

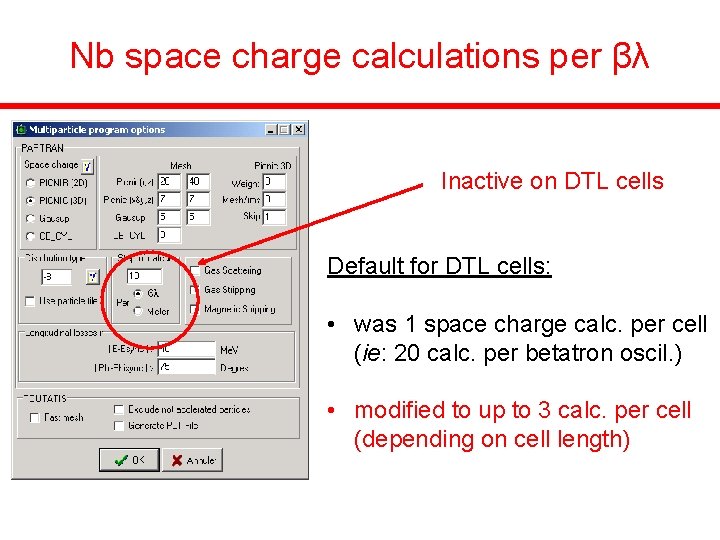
Nb space charge calculations per βλ Inactive on DTL cells Default for DTL cells: • was 1 space charge calc. per cell (ie: 20 calc. per betatron oscil. ) • modified to up to 3 calc. per cell (depending on cell length)

Number of particles • Most simulations use 50 kparticles (1000 runs) – Fast calculation – Minimal loss: 20 ppm • A few global error runs use 106 particles (5000 runs) – 250 to 400 CPU hours – Minimal loss: 1 ppm

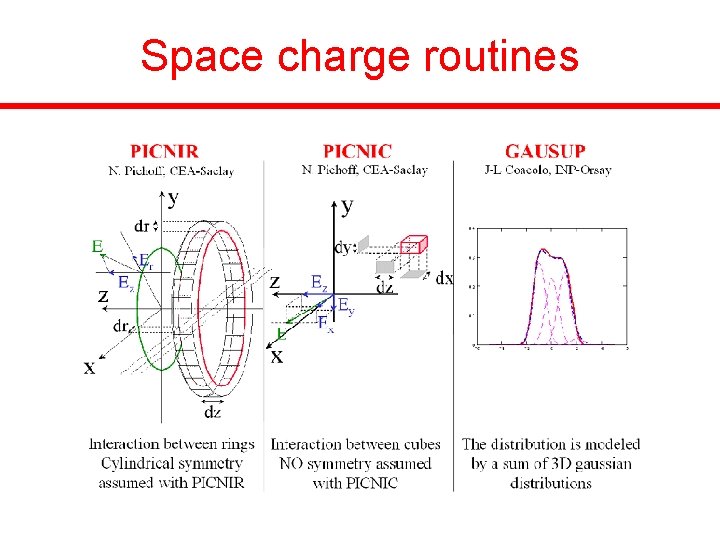
Space charge routines

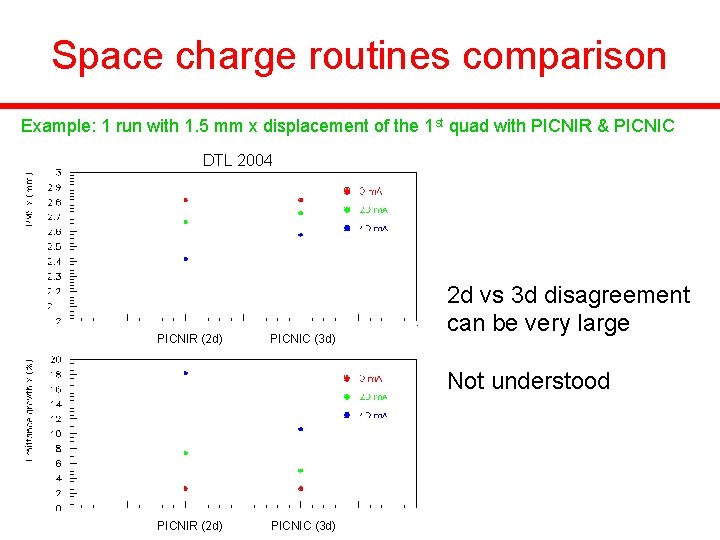
Space charge routines comparison Example: 1 run with 1. 5 mm x displacement of the 1 st quad with PICNIR & PICNIC DTL 2004 PICNIR (2 d) PICNIC (3 d) 2 d vs 3 d disagreement can be very large Not understood PICNIR (2 d) PICNIC (3 d)

Space charge routines disagreement • • • large for large emittance growth if X ≠ Y (our case) increases with beam current much more pronounced for FFDD vs FODO for transverse phenomenon Agreement for longitudinal errors (unexplained) Þ Use 3 d PICNIC with optimized mesh size

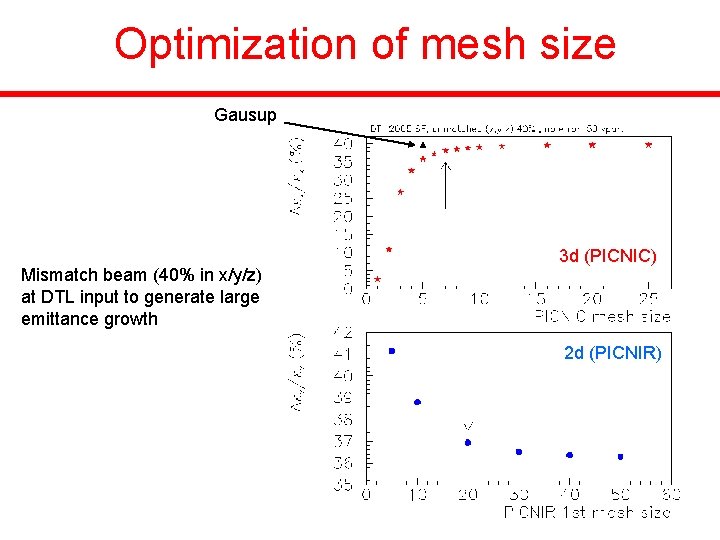
Optimization of mesh size Gausup Mismatch beam (40% in x/y/z) at DTL input to generate large emittance growth 3 d (PICNIC) 2 d (PICNIR)

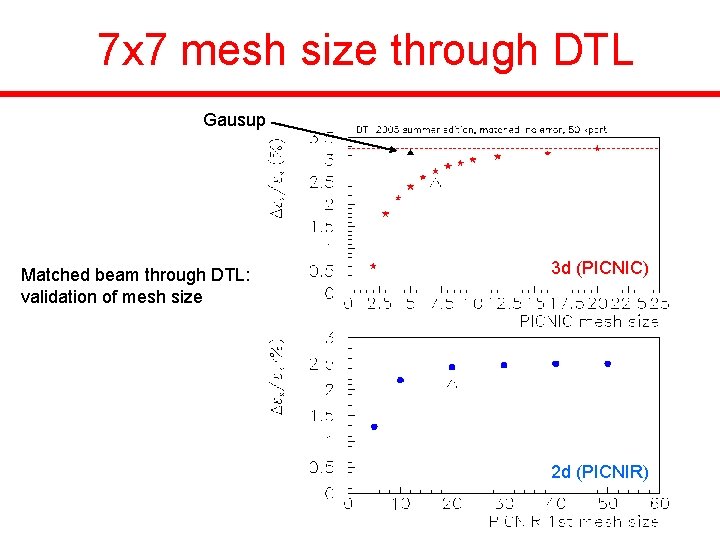
7 x 7 mesh size through DTL Gausup Matched beam through DTL: validation of mesh size 3 d (PICNIC) 2 d (PICNIR)

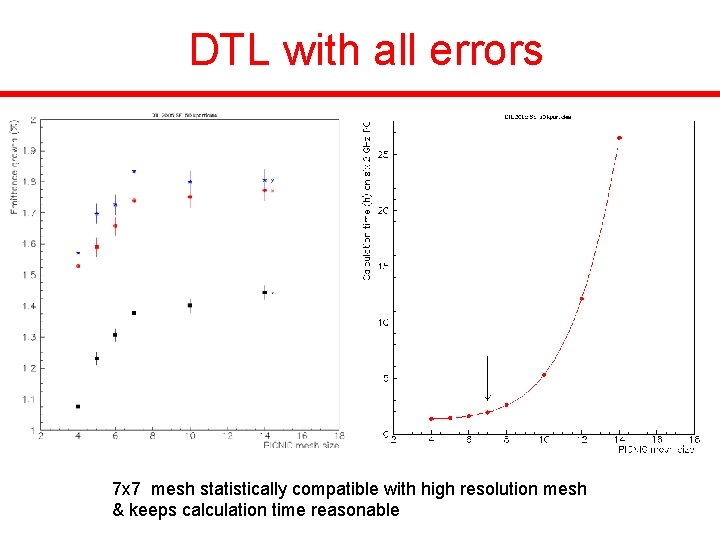
DTL with all errors 7 x 7 mesh statistically compatible with high resolution mesh & keeps calculation time reasonable

Sensitivities to longitudinal errors DTL 2005 Error type Longitudinal errors Max error amplitude (mm or deg) Eklys/Eklys = ± 1% φklys = ± 1 deg Egap/Egap = ± 1% < εx / εx > ± rms (%) < εy / εy > ± rms (%) < εz / εz > ± rms (%) 0. 0 ± 0. 5 0. 0 ± 0. 6 0. 5 ± 0. 7 Gaussian distribution, 50 kpart, 1000 runs Very little effect for all 3 longitudinal errors combined

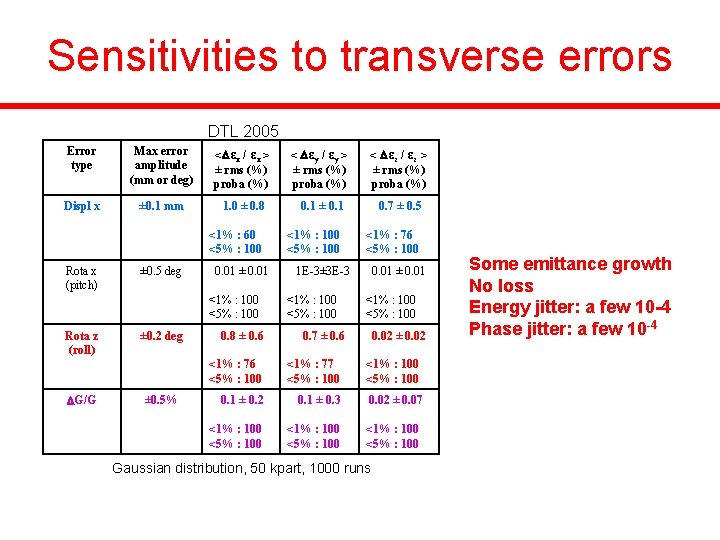
Sensitivities to transverse errors Error type Max error amplitude (mm or deg) Displ x ± 0. 1 mm DTL 2005 < εx / εx > ± rms (%) proba (%) 1. 0 ± 0. 8 <1% : 60 <5% : 100 Rota x (pitch) Rota z (roll) ± 0. 5 deg ± 0. 2 deg ± 0. 5% < εz / εz > ± rms (%) proba (%) 0. 1 ± 0. 1 <1% : 100 <5% : 100 0. 7 ± 0. 5 <1% : 76 <5% : 100 0. 01 ± 0. 01 1 E-3± 3 E-3 0. 01 ± 0. 01 <1% : 100 <5% : 100 0. 8 ± 0. 6 <1% : 76 <5% : 100 G/G < εy / εy > ± rms (%) proba (%) 0. 1 ± 0. 2 <1% : 100 <5% : 100 0. 7 ± 0. 6 0. 02 ± 0. 02 <1% : 77 <5% : 100 0. 1 ± 0. 3 <1% : 100 <5% : 100 0. 02 ± 0. 07 <1% : 100 <5% : 100 Gaussian distribution, 50 kpart, 1000 runs Some emittance growth No loss Energy jitter: a few 10 -4 Phase jitter: a few 10 -4

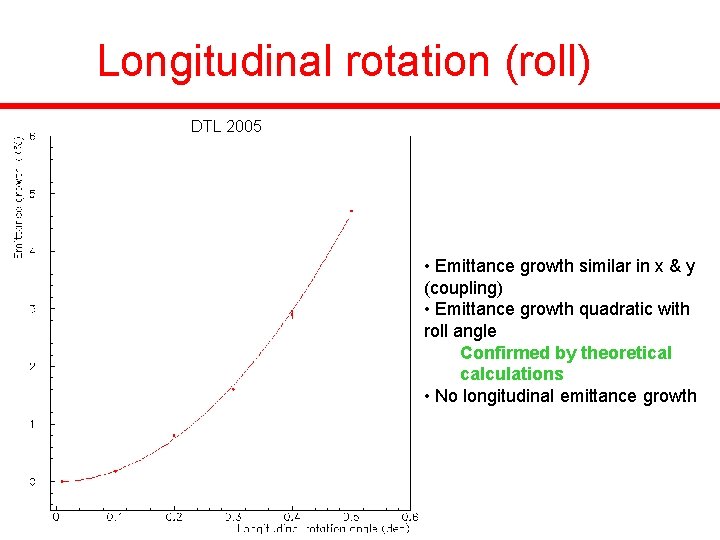
Longitudinal rotation (roll) DTL 2005 • Emittance growth similar in x & y (coupling) • Emittance growth quadratic with roll angle Confirmed by theoretical calculations • No longitudinal emittance growth

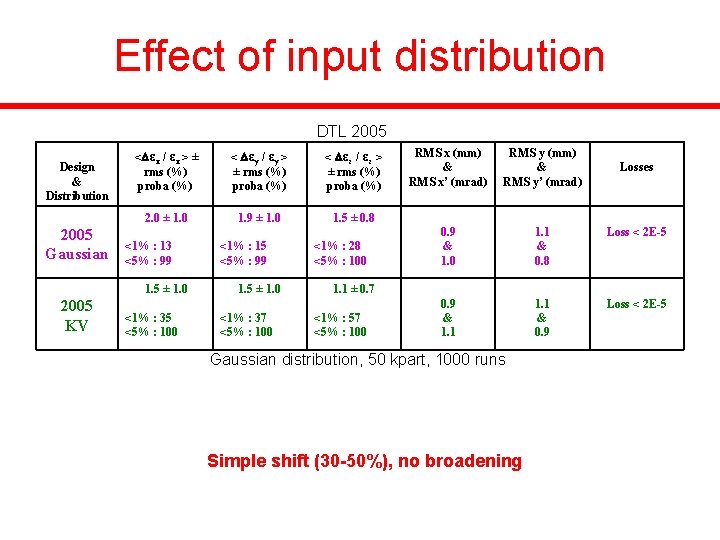
Effect of input distribution Design & Distribution 2005 Gaussian < εx / εx > ± rms (%) proba (%) < εy / εy > ± rms (%) proba (%) 2. 0 ± 1. 0 1. 9 ± 1. 0 <1% : 13 <5% : 99 1. 5 ± 1. 0 2005 KV <1% : 35 <5% : 100 <1% : 15 <5% : 99 1. 5 ± 1. 0 <1% : 37 <5% : 100 DTL 2005 < εz / εz > ± rms (%) proba (%) RMS x (mm) & RMS x’ (mrad) RMS y (mm) & RMS y’ (mrad) 0. 9 & 1. 0 1. 1 & 0. 8 0. 9 & 1. 1 & 0. 9 1. 5 ± 0. 8 <1% : 28 <5% : 100 1. 1 ± 0. 7 <1% : 57 <5% : 100 Gaussian distribution, 50 kpart, 1000 runs Simple shift (30 -50%), no broadening Losses Loss < 2 E-5

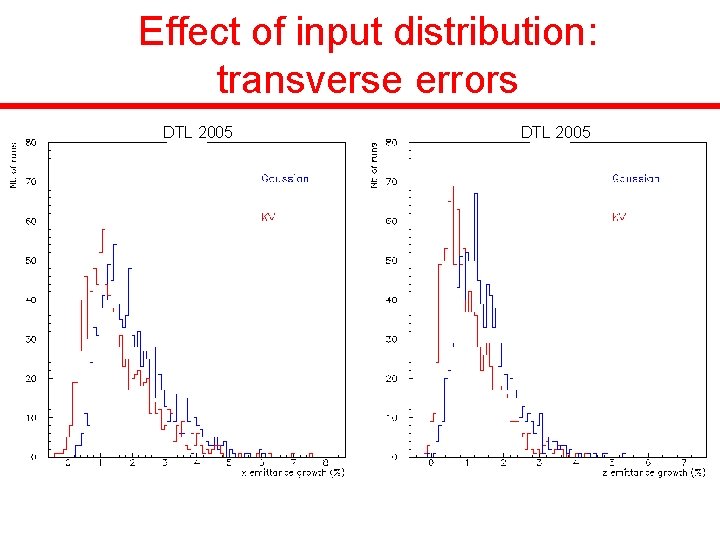
Effect of input distribution: transverse errors DTL 2005

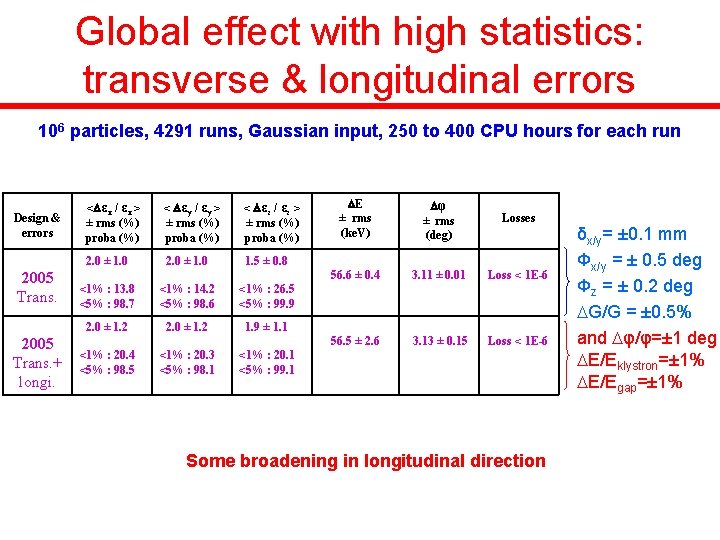
Global effect with high statistics: transverse & longitudinal errors 106 particles, 4291 runs, Gaussian input, 250 to 400 CPU hours for each run Design & errors < εx / εx > ± rms (%) proba (%) 2. 0 ± 1. 0 2005 Trans. + longi. < εy / εy > ± rms (%) proba (%) 2. 0 ± 1. 0 < εz / εz > ± rms (%) proba (%) E ± rms (ke. V) φ ± rms (deg) 56. 6 ± 0. 4 3. 11 ± 0. 01 Loss < 1 E-6 56. 5 ± 2. 6 3. 13 ± 0. 15 Loss < 1 E-6 1. 5 ± 0. 8 <1% : 13. 8 <5% : 98. 7 <1% : 14. 2 <5% : 98. 6 <1% : 26. 5 <5% : 99. 9 2. 0 ± 1. 2 1. 9 ± 1. 1 <1% : 20. 4 <5% : 98. 5 <1% : 20. 3 <5% : 98. 1 <1% : 20. 1 <5% : 99. 1 Losses Some broadening in longitudinal direction δx/y= ± 0. 1 mm Φx/y = ± 0. 5 deg Φz = ± 0. 2 deg G/G = ± 0. 5% and φ/φ=± 1 deg E/Eklystron=± 1% E/Egap=± 1%

Main trends of quadrupole alignment • Transverse displacement (symmetric x/y ) transverse & longitudinal emit. growth 2005 design: ~ 1% for ± 0. 1 mm • Transverse rotation (pitch & yaw): no effect • Longitudinal rotation (roll): transverse emit. growth 2005 design: ~ 0. 8% for ± 0. 2 deg • Emittance growth with 2005 design vs 2004 design: slightly worse with errors on all tanks • Individual sensitivities roughly add up

DTL tank 1 tolerances Tolerances agreed upon by DTL task force: • quadrupoles: longitudinal displacements: δx, y = ± 0. 1 mm longitudinal rotations: Φ x, y = ± 0. 5 deg transverse rotations: Φ z = ± 0. 2 deg gradient: G/G = ± 0. 5% • accelerating field: klystron field amplitude: Eklys/Eklys = ± 1% klystron field phase: φklys = ± 1 deg gap field amplitude: Egap/Egap = ± 1%

Conclusions • Sensitive parameters: transverse displacement & roll • Little effect due to longitudinal errors (longitudinal shift cannot be tested with TW) • With present tolerance budget, beam quality sees little degradation through DTL: Emittance growth x, y and z < 5% in 98% of runs Loss < 10 -6 RMS width in x and y < 1. 2 mm RMS width in x’ and y’ < 1. 1 mrad • Multipolar component contribution: waiting for TW debug • Code benchmarking to validate results

Acknowledgements • Didier URIOT (CEA/DSM) for discussions and multiple debugs • Nicolas PICHOFF (CEA/DAM) for discussions regarding space charge calculations • Edgar Sargsyan, Alessandra Lombardi and Frank Gerigk (CERN) for inputs and discussions