Code Optimization Introduction l l Criteria for CodeImproving

Code Optimization

Introduction l l Criteria for Code-Improving Transformation: – Meaning must be preserved (correctness) – Speedup must occur on average – Work done must be worth the effort Opportunities: – Programmer (algorithm, directives) – Intermediate code – Target code 29 -Sep-20

l l Machine Independent Machine Dependent 29 -Sep-20

Basic Blocks A basic block is a sequence of consecutive statements in which flow of control enters at the beginning and leaves at the end without halt or possibly of the branching except at the end. 29 -Sep-20

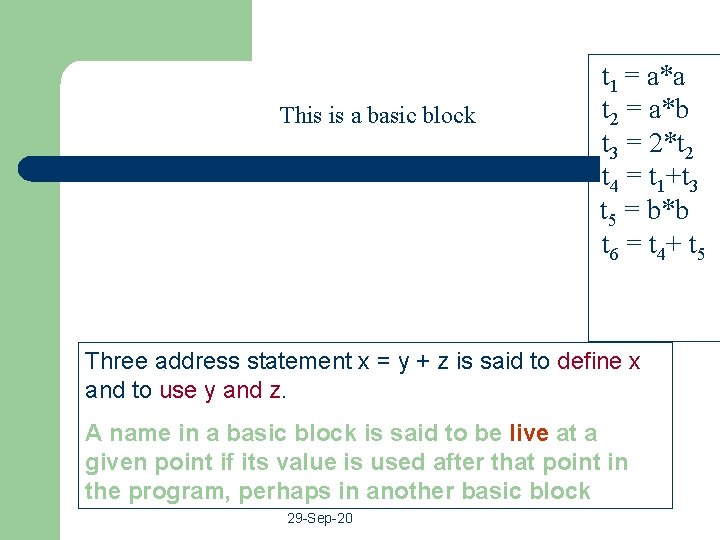
This is a basic block t 1 = a*a t 2 = a*b t 3 = 2*t 2 t 4 = t 1+t 3 t 5 = b*b t 6 = t 4+ t 5 Three address statement x = y + z is said to define x and to use y and z. A name in a basic block is said to be live at a given point if its value is used after that point in the program, perhaps in another basic block 29 -Sep-20

Partition into basic blocks Method – We first determine the set of leaders l The first statement is a leader. l Any statement that is the target of a conditional or unconditional goto is a leader. l Any statement that immediately follows a goto or unconditional goto statement is a leader. For each leader, its basic block consists of the leader and all the statements up to but not including the next leader or the end of the program. 29 -Sep-20

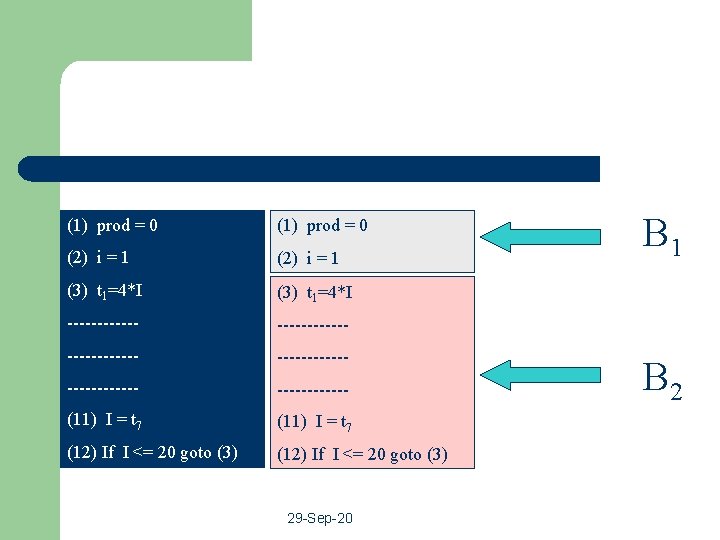
(1) prod = 0 (2) i = 1 (3) t 1=4*I ------------ ------------ (11) I = t 7 (12) If I <= 20 goto (3) 29 -Sep-20 B 1 B 2

Transformations on Basic Blocks l l A code-improving transformation is a code optimization to improve speed or reduce code size Global transformations are performed across basic blocks Local transformations are only performed on single basic blocks Transformations must be safe and preserve the meaning of the code – A local transformation is safe if the transformed basic block is guaranteed to be equivalent to its original form 29 -Sep-20

Classic Examples of Local and Global Code Optimizations l Local – – – l Constant folding Constant combining Strength reduction Constant propagation Common subexpression elimination Backward copy propagation Global – – – – 29 -Sep-20 Dead code elimination Constant propagation Forward copy propagation Common subexpression elimination Code motion Loop strength reduction Induction variable elimination

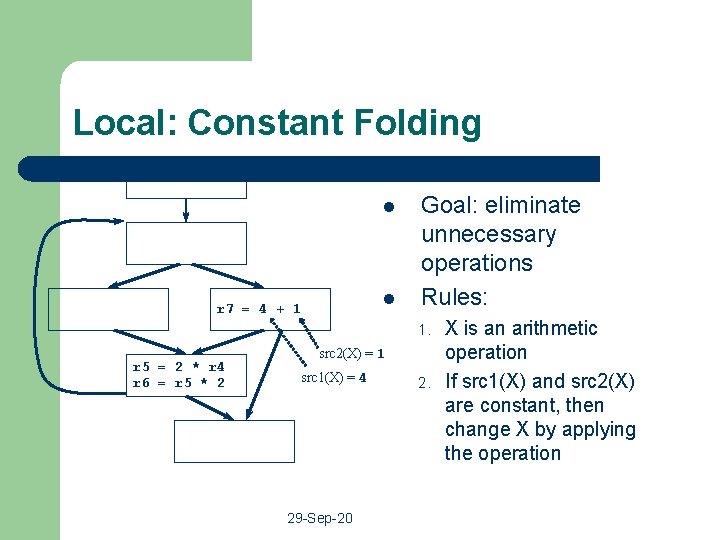
Local: Constant Folding l l r 7 = 4 + 1 Goal: eliminate unnecessary operations Rules: 1. r 5 = 2 * r 4 r 6 = r 5 * 2 src 2(X) = 1 src 1(X) = 4 29 -Sep-20 2. X is an arithmetic operation If src 1(X) and src 2(X) are constant, then change X by applying the operation

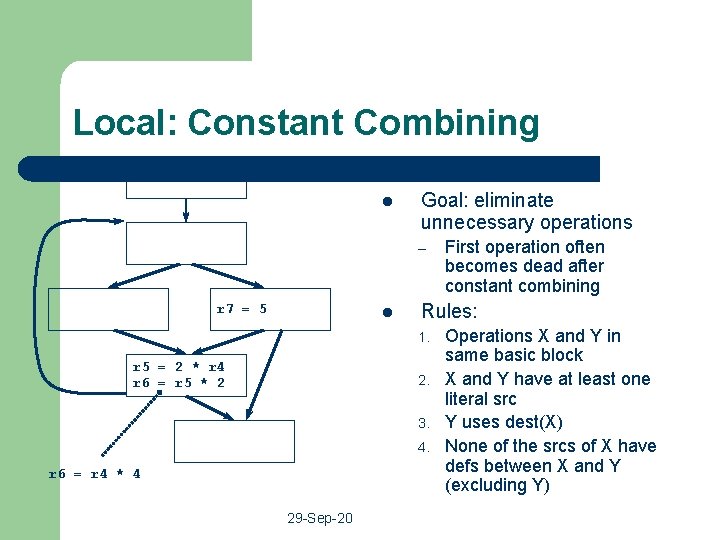
Local: Constant Combining l Goal: eliminate unnecessary operations – r 7 = 5 l Rules: 1. r 5 = 2 * r 4 r 6 = r 5 * 2 2. 3. 4. r 6 = r 4 * 4 29 -Sep-20 First operation often becomes dead after constant combining Operations X and Y in same basic block X and Y have at least one literal src Y uses dest(X) None of the srcs of X have defs between X and Y (excluding Y)

Local: Strength Reduction l l r 7 = 5 Goal: replace expensive operations with cheaper ones Rules (common): 1. r 5 = 2 * r 4 r 6 = r 4 * 4 2. r 5 = r 4 + r 4 3. r 6 = r 4 << 2 29 -Sep-20 X is an multiplication operation where src 1(X) or src 2(X) is a const 2 k integer literal Change X by using shift operation For k=1 can use add

Local: Constant Propagation r 1 = 5 r 2 = _x r 3 = 7 r 4 = r 4 r 1 = r 1 r 3 = 12 r 8 = r 1 r 9 = r 3 = r 2 r 7 = r 3 M[r 7] = l + r 1 + r 2 + 1 r 4 = r 4 + 5 r 1 = 5 + _x + 1 + + 0 r 8 r 9 r 3 r 7 r 2 r 5 1 r 1 = = 5 + _x + 1 - _x l 12 + r 5 _x + 1 - 5 - _x - 1 Goal: replace register uses with literals (constants) in a single basic block Rules: 1. 2. 3. 4. 29 -Sep-20 Operation X is a move to register with src 1(X) literal Operation Y uses dest(X) There is no def of dest(X) between X and Y (excluding defs at X and Y) Replace dest(X) in Y with src 1(X)

Local: Common Subexpression Elimination (CSE) r 1 r 4 r 1 r 6 r 2 r 5 r 7 r 5 = = = = r 2 r 4 6 r 2 r 1 r 4 r 2 r 1 l + r 3 + 1 Goal: eliminate re-computations of an expression – + + + - r 3 1 1 r 3 1 – r 5 = r 2 l More efficient code Resulting moves can get copy propagated (see later) Rules: 1. 2. 3. 4. 5. Operations X and Y have the same opcode and Y follows X src(X) = src(Y) for all srcs For all srcs, no def of a src between X and Y (excluding Y) No def of dest(X) between X and Y (excluding X and Y) Replace Y with move dest(Y) = dest(X) 29 -Sep-20

Local: Backward Copy Propagation r 1 r 2 r 4 r 6 r 9 r 7 r 5 r 4 r 8 = = = = = r 8 r 9 r 2 r 1 r 6 r 7 0 r 2 + r 9 + r 1 + 1 l r 7 = r 2 + 1 Goal: propagate LHS of moves backward – + 1 remove r 7 = r 6 l Rules (dataflow required) 1. 2. + r 7 3. r 7 not live 4. 5. 6. 7. 29 -Sep-20 Eliminates useless moves X and Y in same block Y is a move to register dest(X) is a register that is not live out of the block Y uses dest(X) dest(Y) not used or defined between X and Y (excluding X and Y) No uses of dest(X) after the first redef of dest(Y) Replace src(Y) on path from X to Y with dest(X) and remove Y

Global: Dead Code Elimination r 1 = 3 r 2 = 10 l r 4 = r 4 + 1 r 7 = r 1 * r 4 r 3 = r 3 + 1 r 7 not live l Goal: eliminate any operation who’s result is never used Rules (dataflow required) 1. r 2 = 0 2. l r 3 = r 2 + r 1 Rules too simple! – – M[r 1] = r 3 29 -Sep-20 X is an operation with no use in def-use (DU) chain, i. e. dest(X) is not live Delete X if removable (not a mem store or branch) Misses deletion of r 4, even after deleting r 7, since r 4 is live in loop Better is to trace UD chains backwards from “critical” operations

Global: Constant Propagation r 1 = 4 r 2 = 10 l r 5 = 2 r 7 = r 1 * r 5 r 7 = 8 l Goal: globally replace register uses with literals Rules (dataflow required) 1. r 3 = r 3 + r 5 r 2 = 0 2. 3. r 3 = r 2 + r 1 r 6 = r 7 * r 4 r 3 = r 2 + 4 r 6 = 8 * r 4 4. r 3 = r 3 + 2 M[r 1] = r 3 M[4] = r 3 29 -Sep-20 X is a move to a register with src 1(X) literal Y uses dest(X) has only one def at X for use-def (UD) chains to Y Replace dest(X) in Y with src 1(X)

Global: Forward Copy Propagation l r 1 = r 2 r 3 = r 4 Goal: globally propagate RHS of moves forward – – r 6 = r 3 + 1 l r 2 = 0 Rules (dataflow required) 1. r 5 = r 2 + r 3 r 5 = r 2 + r 4 2. 3. r 6 = r 4 + 1 4. 5. 29 -Sep-20 Reduces dependence chain May be possible to eliminate moves X is a move with src 1(X) register Y uses dest(X) has only one def at X for UD chains to Y src 1(X) has no def on any path from X to Y Replace dest(X) in Y with src 1(X)

Global: Common Subexpression Elimination (CSE) r 1 = r 2 * r 6 l r 3 = r 4 / r 7 r 10 = r 3 l r 2 = r 2 + 1 r 3 = r 3 + 1 Goal: eliminate recomputations of an expression Rules: 1. r 1 = r 3 * 7 2. r 5 = r 2 * r 6 r 8 = r 4 / r 7 3. r 8 = r 10 4. r 9 = r 3 * 7 5. 29 -Sep-20 X and Y have the same opcode and X dominates Y src(X) = src(Y) for all srcs For all srcs, no def of a src on any path between X and Y (excluding Y) Insert rx = dest(X) immediately after X for new register rx Replace Y with move dest(Y) = rx

Global: Code Motion preheader r 1 = 0 r 4 = M[r 5] r 7 = r 4 * 3 l header l Goal: move loop-invariant computations to preheader Rules: 1. r 8 = r 2 + 1 r 7 = r 8 * r 4 r 3 = r 2 + 1 2. 3. r 1 = r 1 + r 7 4. 5. M[r 1] = r 3 6. 29 -Sep-20 Operation X in block that dominates all exit blocks X is the only operation to modify dest(X) in loop body All srcs of X have no defs in any of the basic blocks in the loop body Move X to end of preheader Note 1: if one src of X is a memory load, need to check for stores in loop body Note 2: X must be movable and not cause exceptions

Global: Loop Strength Reduction B 1: i : = 0 t 1 : = n-2 t 2 : = 4*i B 2: t 2 : = 4*i A[t 2] : = 0 i : = i+1 B 2: A[t 2] : = 0 i : = i+1 t 2 : = t 2+4 B 3: if i < t 1 goto B 2 Replace expensive computations with induction variables 29 -Sep-20

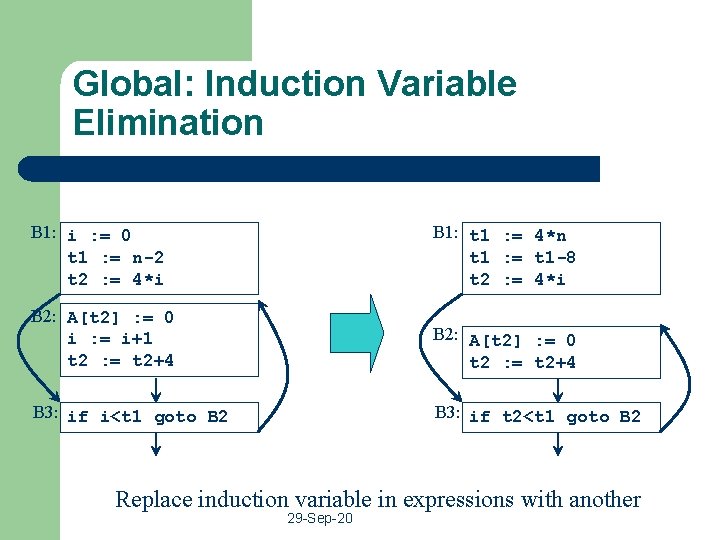
Global: Induction Variable Elimination B 1: i : = 0 t 1 : = n-2 t 2 : = 4*i B 1: t 1 : = 4*n t 1 : = t 1 -8 t 2 : = 4*i B 2: A[t 2] : = 0 i : = i+1 t 2 : = t 2+4 B 2: A[t 2] : = 0 t 2 : = t 2+4 B 3: if i<t 1 goto B 2 B 3: if t 2<t 1 goto B 2 Replace induction variable in expressions with another 29 -Sep-20

Flow Graphs l l l A graph representation of three address statements, called flow graph. Nodes in the flow graph represent computations Edges represent the flow of control 29 -Sep-20

l Flow graph: – – We can add flow of control information to the set of basic blocks making up a program by constructing directed graph called flow graph. There is a directed edge from block B 1 to block B 2 if l l There is conditional or unconditional jump from the last statement of B 1 to the first statement of B 2 or B 2 immediately follows B 1 in the order of the program, and B 1 does not end in an unconditional jump. 29 -Sep-20

Loops l A loop is a collection of nodes in a flow graph such that – – All nodes in the collection are strongly connected, that is from any node in the loop to any other, there is a path of length one or more, wholly within the loop, and The collection of nodes has a unique entry, that is, a node in the loop such that, the only way to reach a node from a node outside the loop is to first go through the entry. 29 -Sep-20

DAG Representation? l l l l l 1 2 3 4 5 6 7 8 9 10 A = 4*i B = a[A] C = 4*i D = b[C] E=B*D F = prod + E Prod = F G=i+1 i=G if I <= 20 goto (1) 29 -Sep-20

DAG representation of Basic Block + * prod <= [] [] a b 4 29 -Sep-20 20 + * i 0 1

Common expression can be eliminated Simple example: a[i+1] = b[i+1] l l t 1 = i+1 t 2 = b[t 1] t 3 = i + 1 a[t 3] = t 2 l l 29 -Sep-20 t 1 = i + 1 t 2 = b[t 1] t 3 = i + 1 a[t 1] = t 2 no longer live

Now, suppose i is a constant: l l i=4 t 1 = i+1 t 2 = b[t 1] a[t 1] = t 2 l l i=4 t 1 = 5 t 2 = b[t 1] a[t 1] = t 2 Final Code: i=4 t 2 = b[5] a[5] = t 2 29 -Sep-20 i=4 t 1 = 5 t 2 = b[5] a[5] = t 2

Simple Loop Optimizations l Code Motion Move invariants out of the loop. Example: while (i <= limit - 2) becomes t : = limit - 2 while (i <= t) 29 -Sep-20

Code for quicksort i = m-1; j = n; v = a[n]; while (1){ do i = i+1; while (a[i] < v); do j = j-1; while (a[j] > v); if (i>=j) break; x = a[i]; a[i] = a[j]; a[j]= x; } x = a[i]; a[i] = a[n]; a[n] = x; 29 -Sep-20

Three Address Code of Quick Sort 1 i=m-1 16 t 7 = 4 * I 2 j=n 17 t 8 = 4 * j 3 t 1 =4 * n 18 t 9 = a[t 8] 4 v = a[t 1] 19 a[t 7] = t 9 5 i=i +1 20 t 10 = 4 * j 6 t 2 = 4 * i 21 a[t 10] = x 7 t 3 = a[t 2] 22 goto (5) 8 if t 3 < v goto (5) 23 t 11 = 4 * I 9 j=j– 1 24 x = a[t 11] 10 t 4 = 4 * j 25 t 12 = 4 * i 11 t 5 = a[t 4] 26 t 13 = 4 * n 12 if t 5 > v goto (9) 27 t 14 = a[t 13] 13 if i >= j goto (23) 28 a[t 12] = t 14 14 t 6 = 4 * i 29 t 15 = 4 * n 15 x = a[t 6] 29 -Sep-20 30 a[t 15] = x

Find The Basic Block 1 i=m-1 16 t 7 = 4 * I 2 j=n 17 t 8 = 4 * j 3 t 1 =4 * n 18 t 9 = a[t 8] 4 v = a[t 1] 19 a[t 7] = t 9 5 i=i +1 20 t 10 = 4 * j 6 t 2 = 4 * i 21 a[t 10] = x 7 t 3 = a[t 2] 22 goto (5) 8 if t 3 < v goto (5) 23 t 11 = 4 * i 9 j=j– 1 24 x = a[t 11] 10 t 4 = 4 * j 25 t 12 = 4 * i 11 t 5 = a[t 4] 26 t 13 = 4 * n 12 if t 5 > v goto (9) 27 t 14 = a[t 13] 13 if i >= j goto (23) 28 a[t 12] = t 14 14 t 6 = 4 * i 29 t 15 = 4 * n 15 x = a[t 6] 30 a[t 15] = x 29 -Sep-20

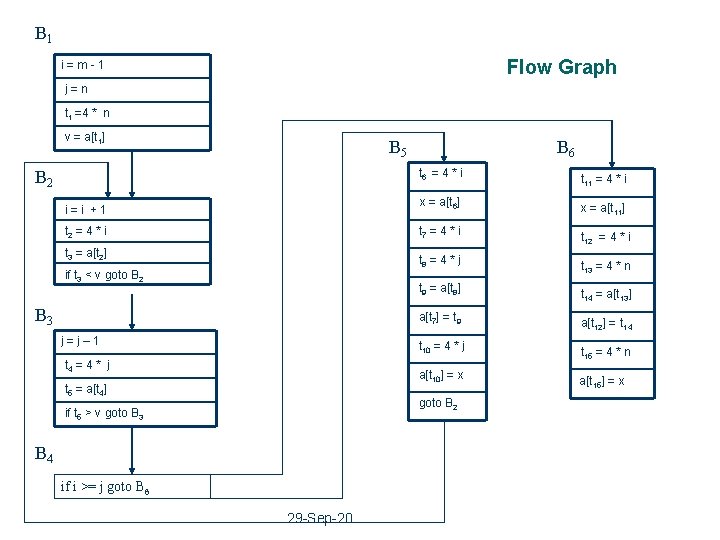
B 1 Flow Graph i=m-1 j=n t 1 =4 * n v = a[t 1] B 5 B 6 t 6 = 4 * i t 11 = 4 * i i=i +1 x = a[t 6] x = a[t 11] t 2 = 4 * i t 7 = 4 * i t 12 = 4 * i t 8 = 4 * j t 13 = 4 * n t 9 = a[t 8] t 14 = a[t 13] a[t 7] = t 9 a[t 12] = t 14 t 10 = 4 * j t 15 = 4 * n a[t 10] = x a[t 15] = x B 2 t 3 = a[t 2] if t 3 < v goto B 2 B 3 j=j– 1 t 4 = 4 * j t 5 = a[t 4] goto B 2 if t 5 > v goto B 3 B 4 if i >= j goto B 6 29 -Sep-20

i=m-1 B 1 j=n t 1 =4 * n v = a[t 1] t 2 = 4 * i a[t 2] = t 5 t 4 = 4 * j B 5 goto B 2 t 2 = t 2 + 4 t 3 = a[t 2] if t 3 < v goto B 2 B 3 t 4 = t 4 - 4 t 5 = a[t 4] if t 5 > v goto B 3 if i >= j goto B 6 B 4 a[t 4] = t 3 29 -Sep-20 t 14 = a[t 1] B 6 a[t 2] = t 14 a[t 1] = t 3

Peephole Optimizations • A Simple but effective technique for locally improving the target code is peephole optimization, • a method for trying to improve the performance of the target program • by examining a short sequence of target instructions and replacing these instructions by a shorter or faster sequence whenever possible. 29 -Sep-20

Peephole Optimizations l Constant Folding x : = 32 x : = x + 32 l becomes Unreachable Code goto L 2 x : = x + 1 No need 29 -Sep-20 x : = 64

l Flow of control optimizations goto L 1 … L 1: goto L 2 Not required if no other L 1 branch becomes goto L 2 29 -Sep-20

l Algebraic Simplification x : = x + 0 No needed l Dead code x : = 32 where x not used after statement y : = x + y y : = y + 32 l Reduction in strength Replace expensive arithmetic operations with cheaper ones x : = x * 2 x : = x + x x : = x << 2 29 -Sep-20