CMU Graduate Complexity Lecture 20 Valiants Theorem Permanent

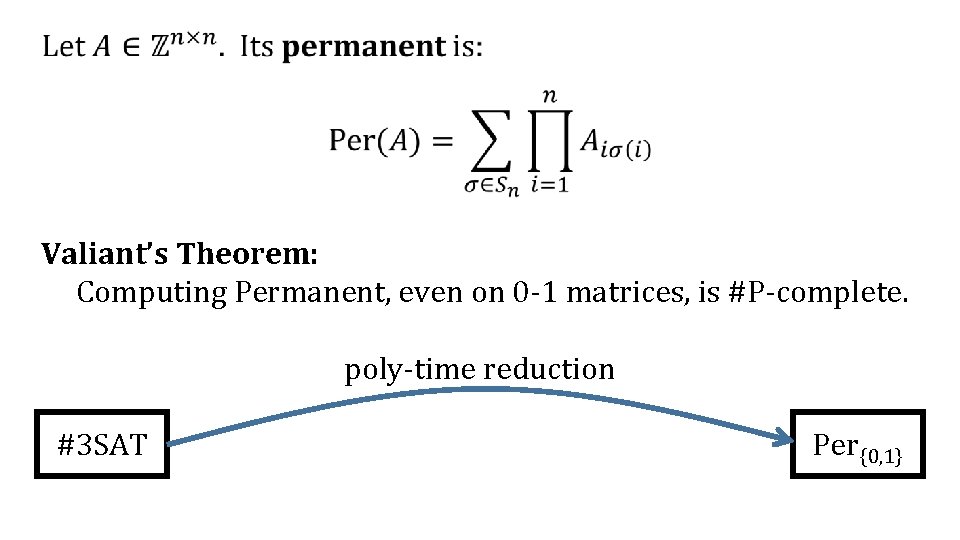
CMU Graduate Complexity Lecture 20 Valiant’s Theorem: Permanent is #P-complete Ryan O’Donnell (Proof exposition from [Dell–Husfeldt–Marx–Taslaman–Wáhlen’ 14 & Bläser’ 15]. )

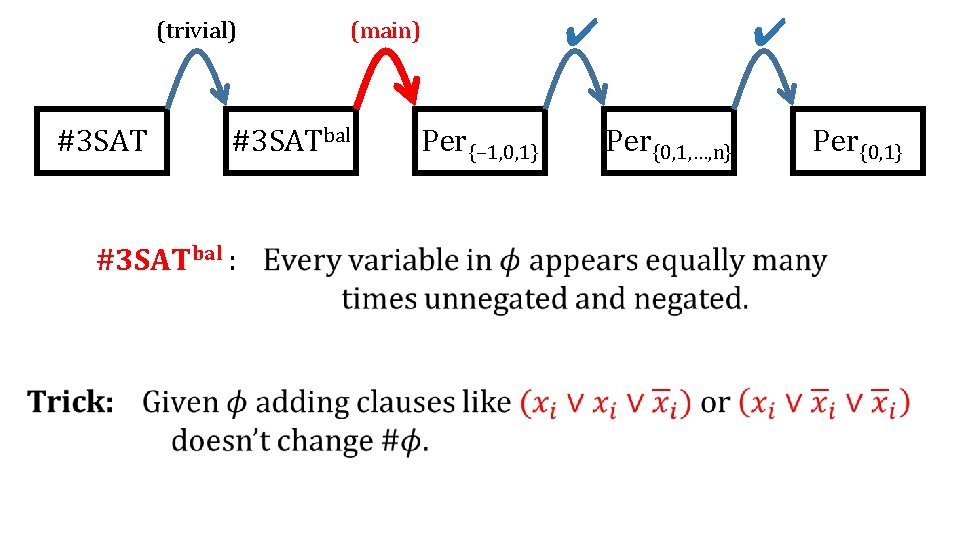
Valiant’s Theorem: Computing Permanent, even on 0 -1 matrices, is #P-complete. poly-time reduction #3 SAT Per{0, 1}

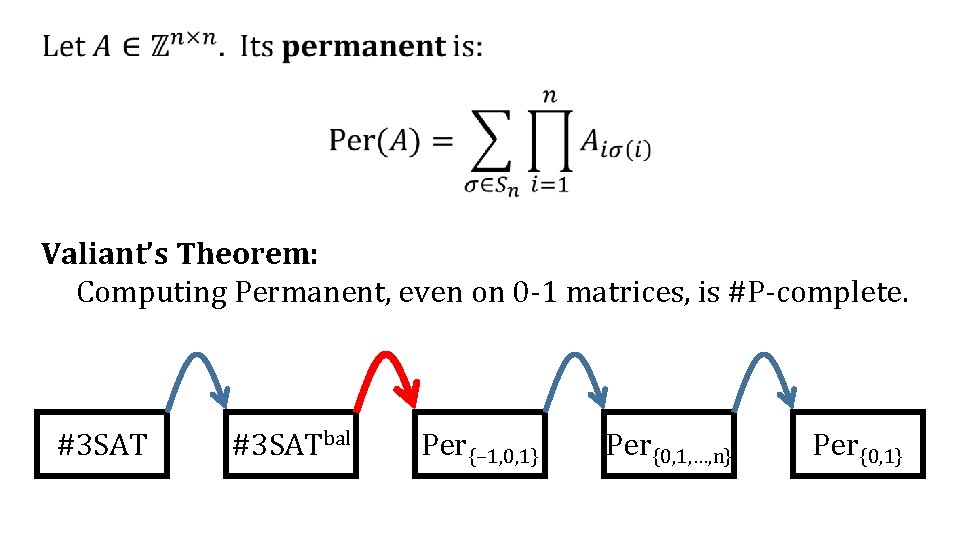
Valiant’s Theorem: Computing Permanent, even on 0 -1 matrices, is #P-complete. #3 SATbal Per{− 1, 0, 1} Per{0, 1, …, n} Per{0, 1}

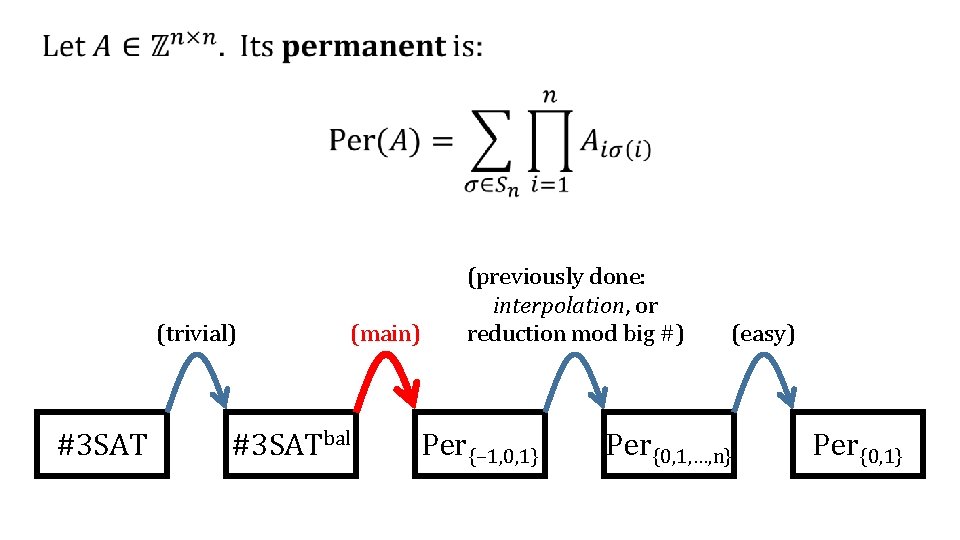
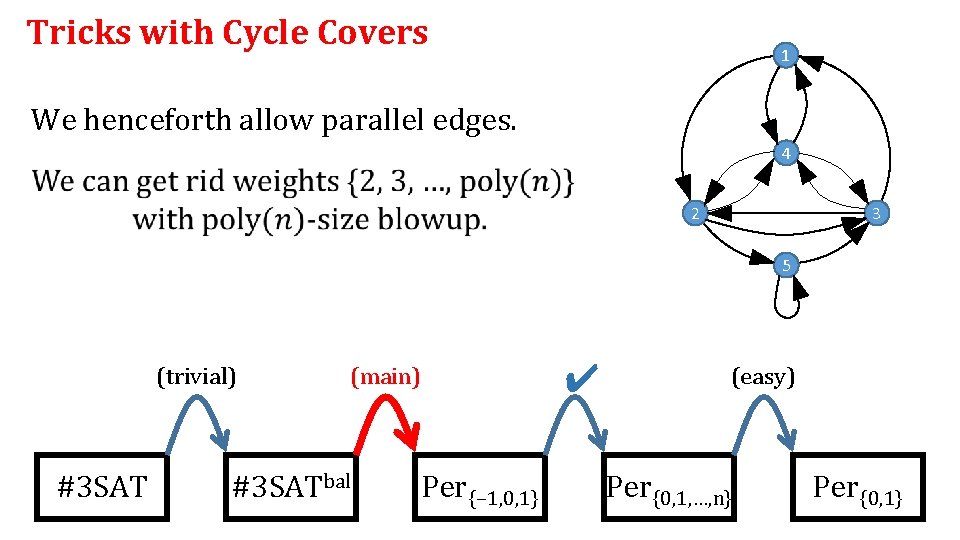
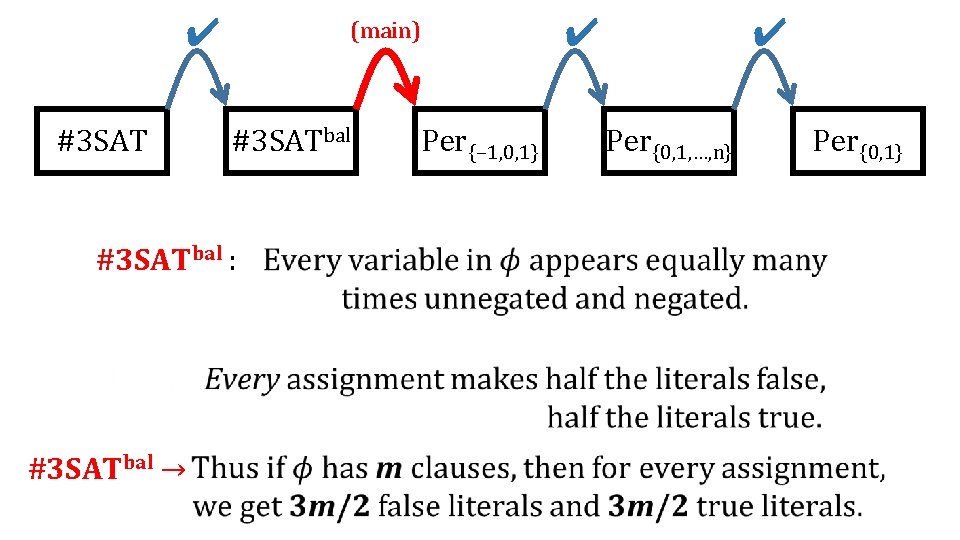
(trivial) #3 SAT (main) #3 SATbal (previously done: interpolation, or reduction mod big #) Per{− 1, 0, 1} (easy) Per{0, 1, …, n} Per{0, 1}

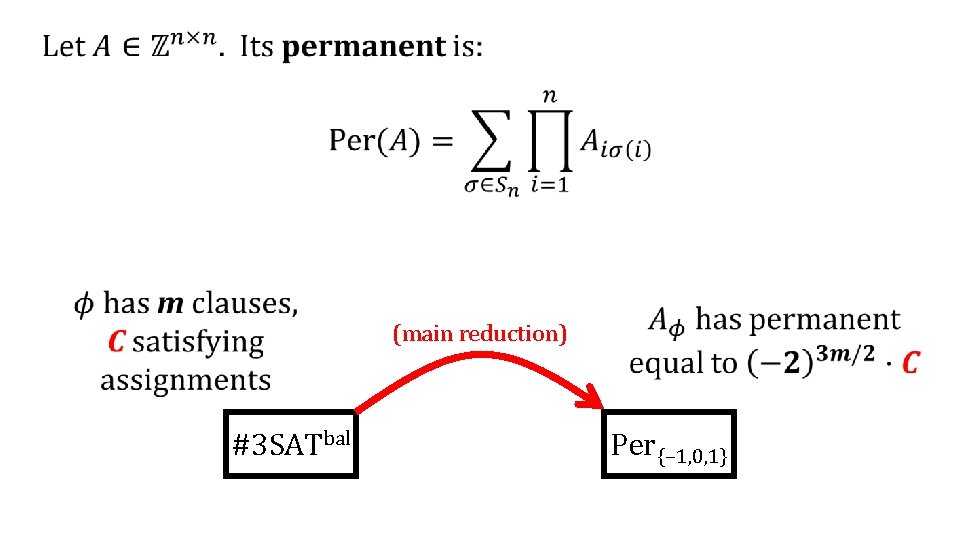
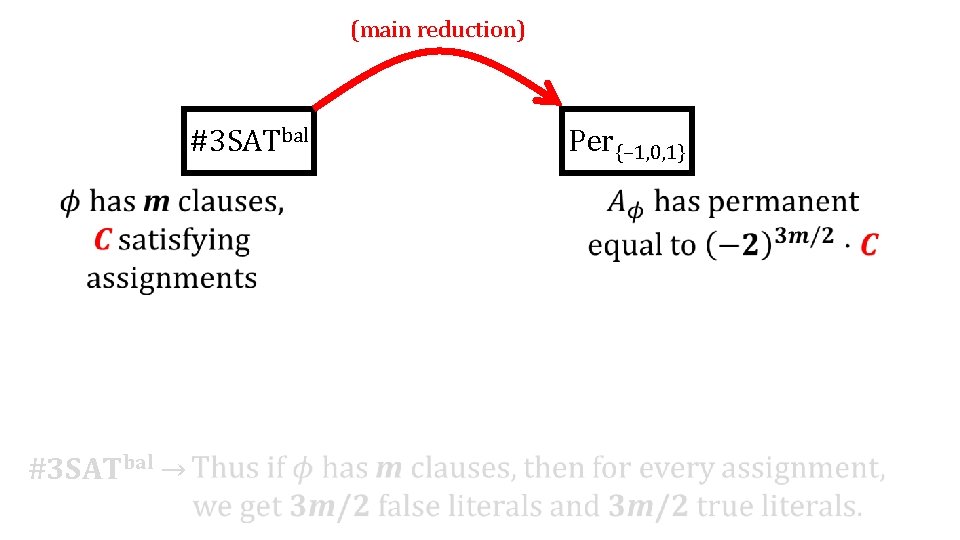
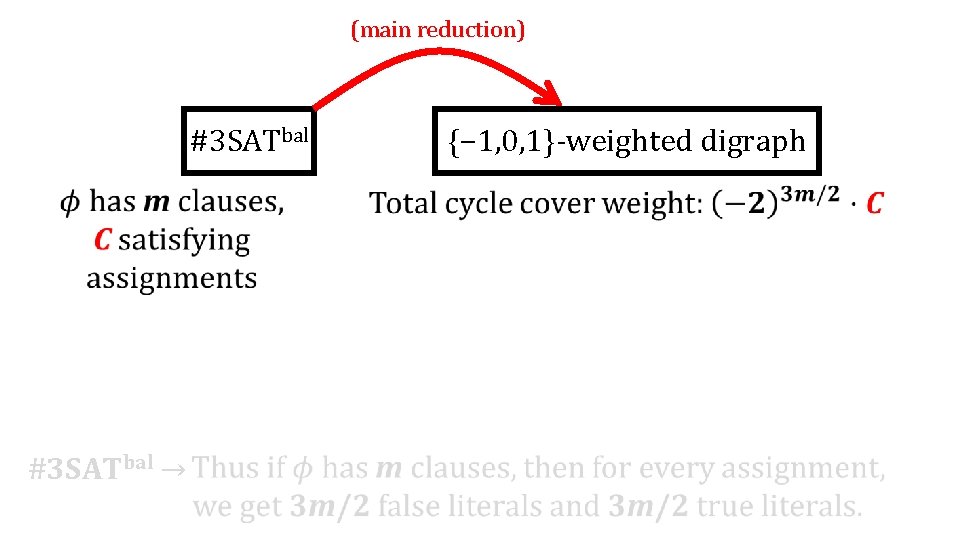
(main reduction) #3 SATbal Per{− 1, 0, 1}

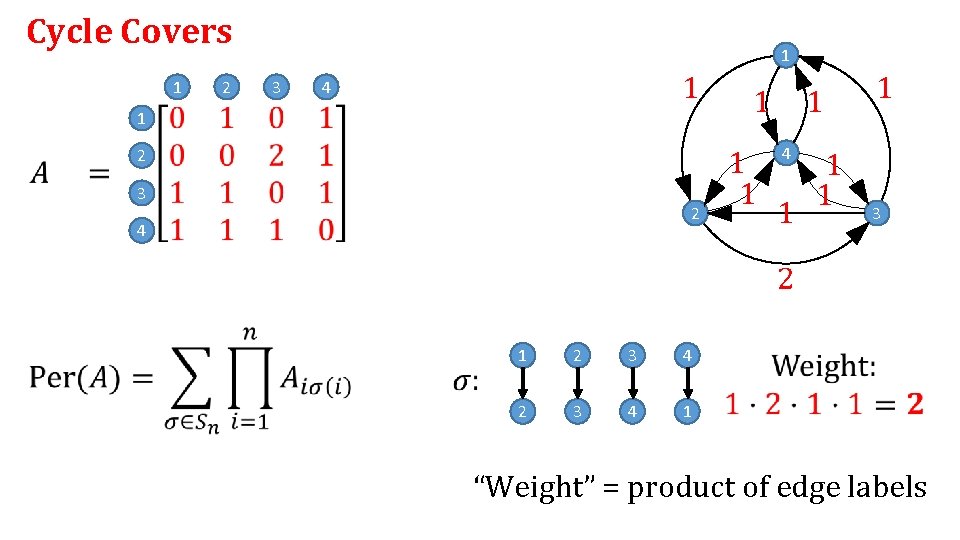
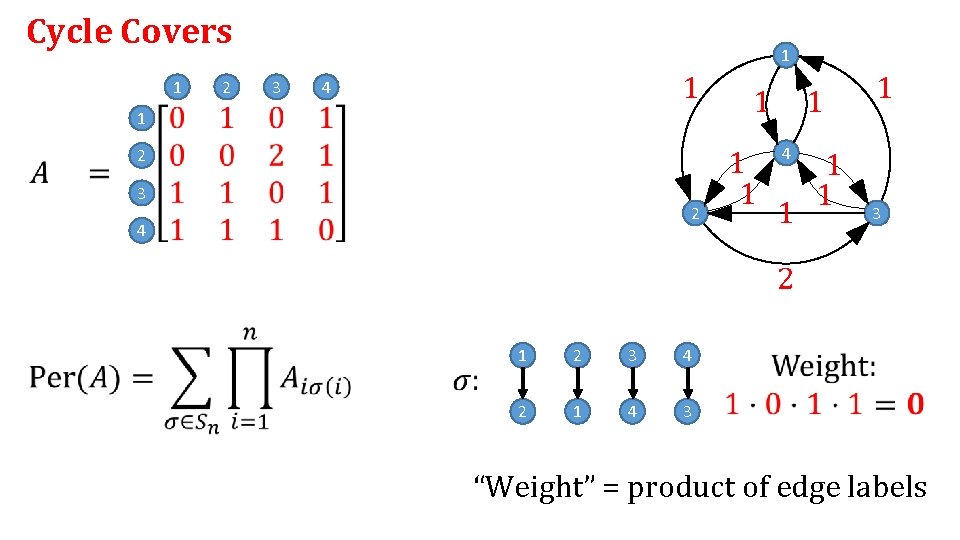
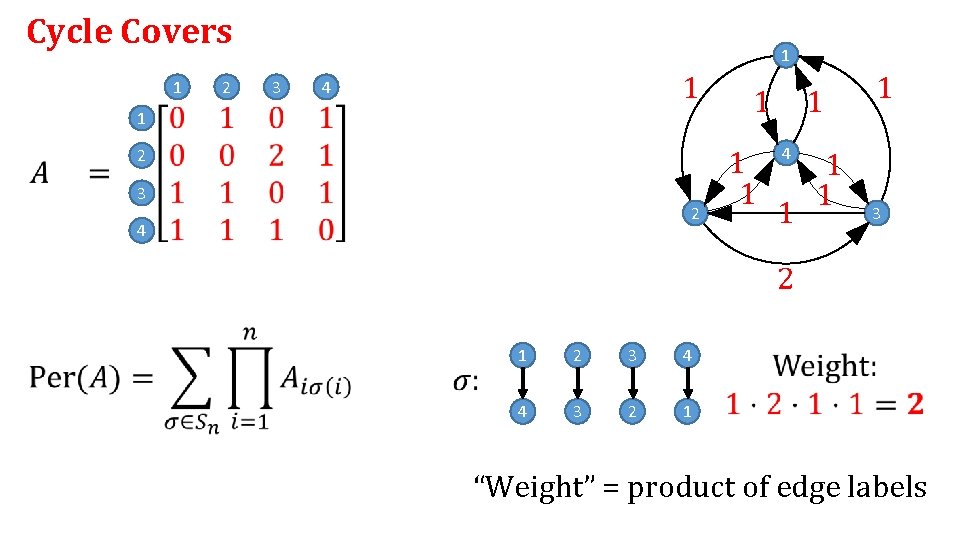
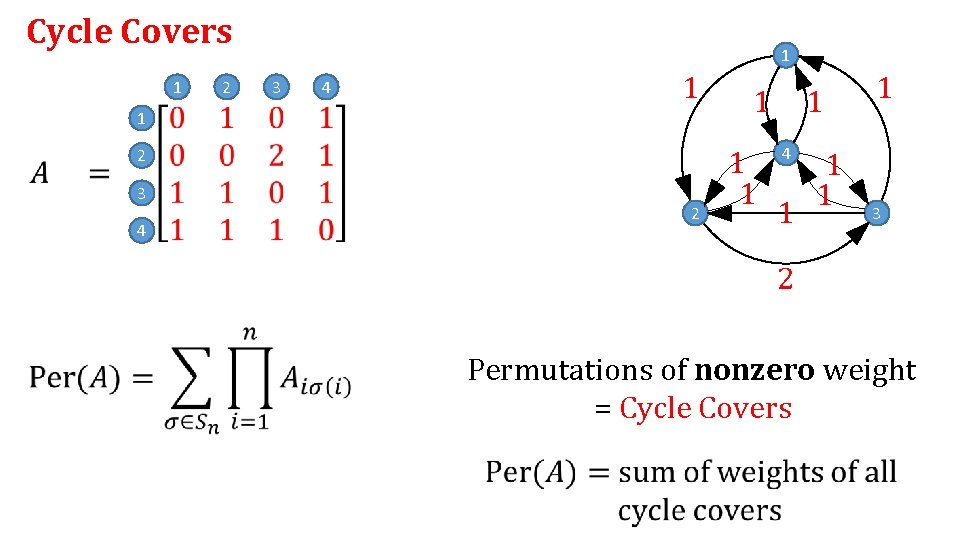
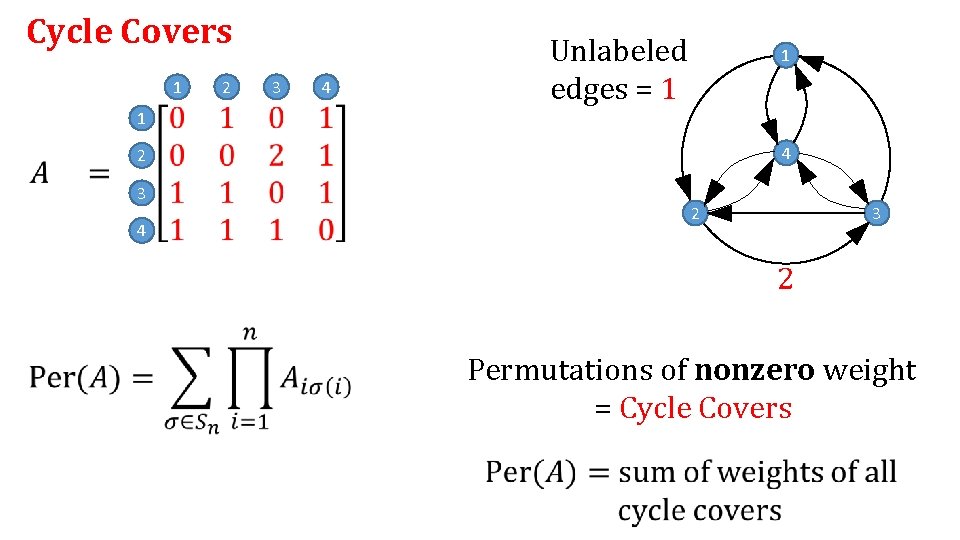
Cycle Covers

Cycle Covers 1 2 1 3 1 4 1 1 2 3 2 4 1 1 1 1 3 2 1 2 3 4 1 “Weight” = product of edge labels

Cycle Covers 1 2 1 3 1 4 1 1 2 3 2 4 1 1 1 1 3 2 1 2 3 4 2 1 4 3 “Weight” = product of edge labels

Cycle Covers 1 2 1 3 1 4 1 1 2 3 2 4 1 1 1 1 3 2 1 2 3 4 4 3 2 1 “Weight” = product of edge labels

Cycle Covers 1 2 1 3 1 4 1 2 3 2 4 1 1 1 1 3 2 Permutations of nonzero weight = Cycle Covers

Cycle Covers 1 2 3 Unlabeled edges = 1 4 1 1 4 2 3 2 4 3 2 Permutations of nonzero weight = Cycle Covers

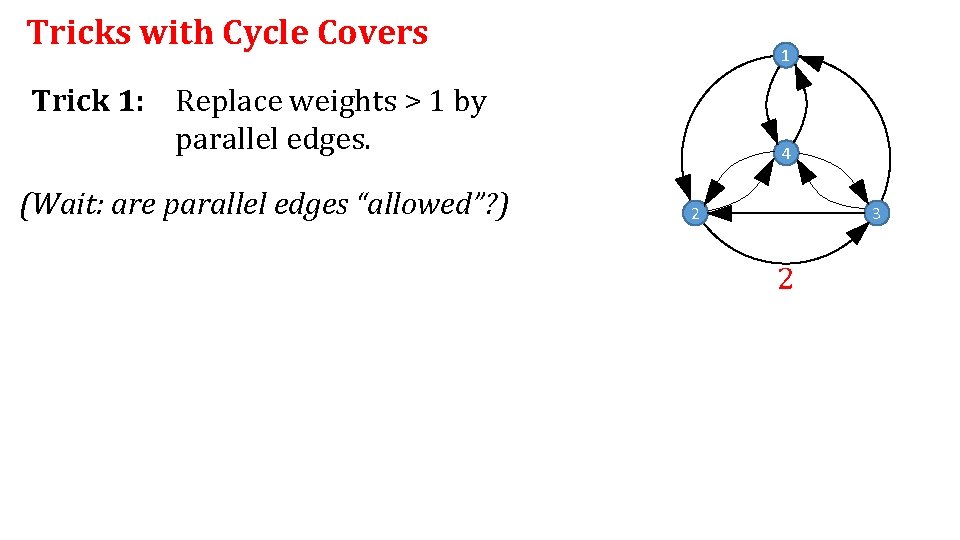
Tricks with Cycle Covers 1 Trick 1: Replace weights > 1 by parallel edges. (Wait: are parallel edges “allowed”? ) 4 2 3 2

Tricks with Cycle Covers 1 Trick 1: Replace weights > 1 by parallel edges. Claim: Total cycle cover weight unchanged. 4 2 3 2

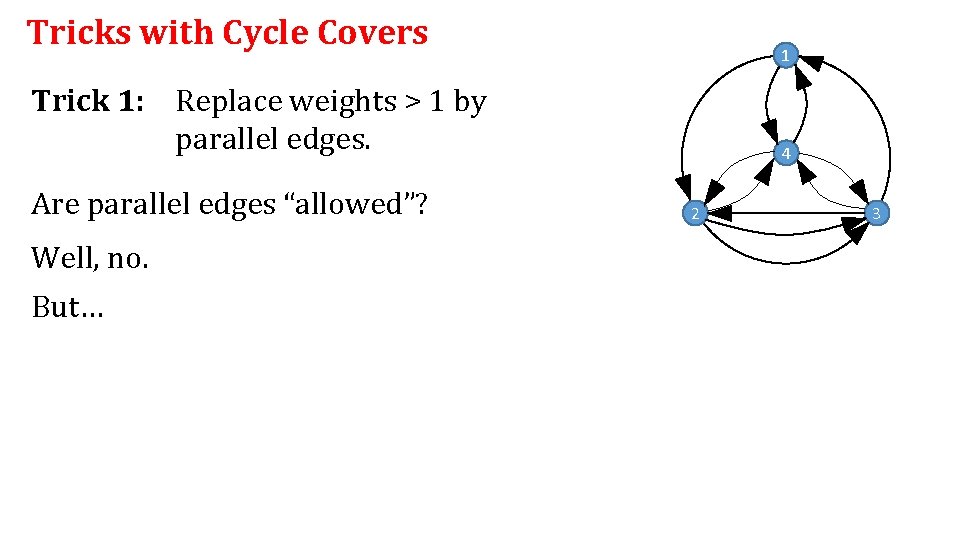
Tricks with Cycle Covers 1 Trick 1: Replace weights > 1 by parallel edges. Are parallel edges “allowed”? Well, no. But… 4 2 3

Tricks with Cycle Covers 1 Trick 2: Can always subdivide any edge, sticking in a self-loop. Claim: Total cycle cover weight unchanged. 4 2 Proof: What are the cycle covers in the new graph? 3 5 Type I: An old cycle cover that didn’t use the subdivided edge: → new same-weight cycle cover by adding the self-loop Type II: An old cycle cover that did use the subdivided edge: → new same-weight cycle cover that takes the length-2 path, avoiding the self-loop.

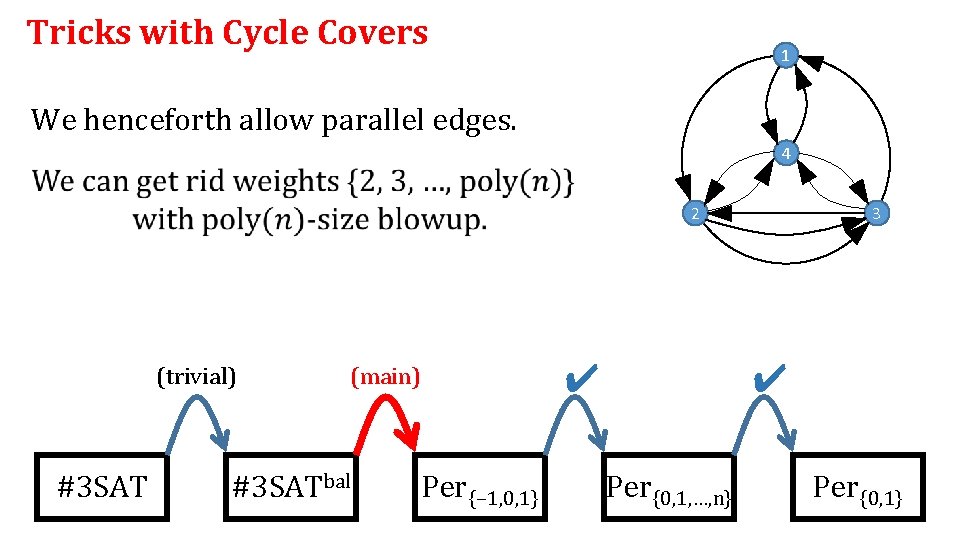
Tricks with Cycle Covers 1 We henceforth allow parallel edges. 4 2 3 5 (trivial) #3 SAT ✔ (main) #3 SATbal Per{− 1, 0, 1} (easy) Per{0, 1, …, n} Per{0, 1}

Tricks with Cycle Covers 1 We henceforth allow parallel edges. 4 2 (trivial) #3 SAT ✔ (main) #3 SATbal Per{− 1, 0, 1} 3 ✔ Per{0, 1, …, n} Per{0, 1}

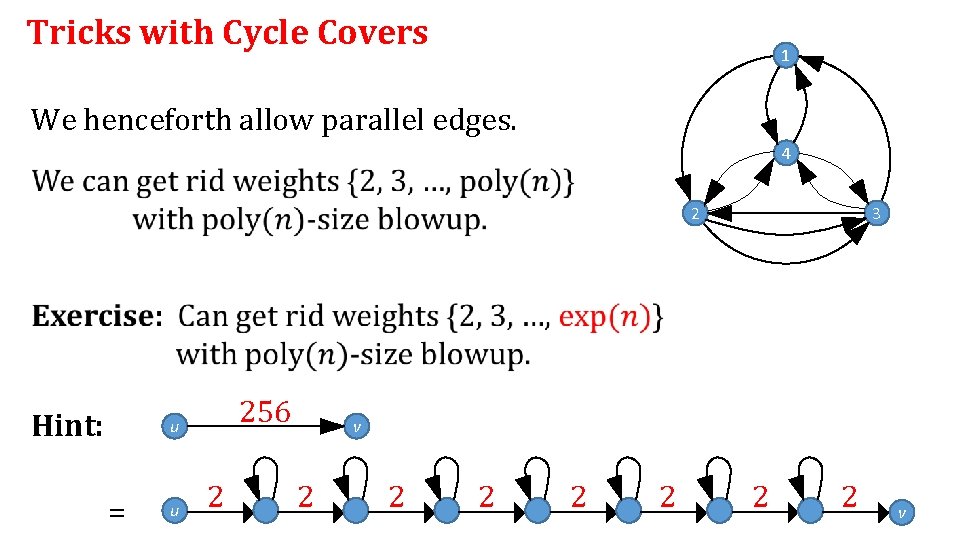
Tricks with Cycle Covers 1 We henceforth allow parallel edges. 4 2 3 Hint: 256 u = u 2 v 2 2 2 2 v

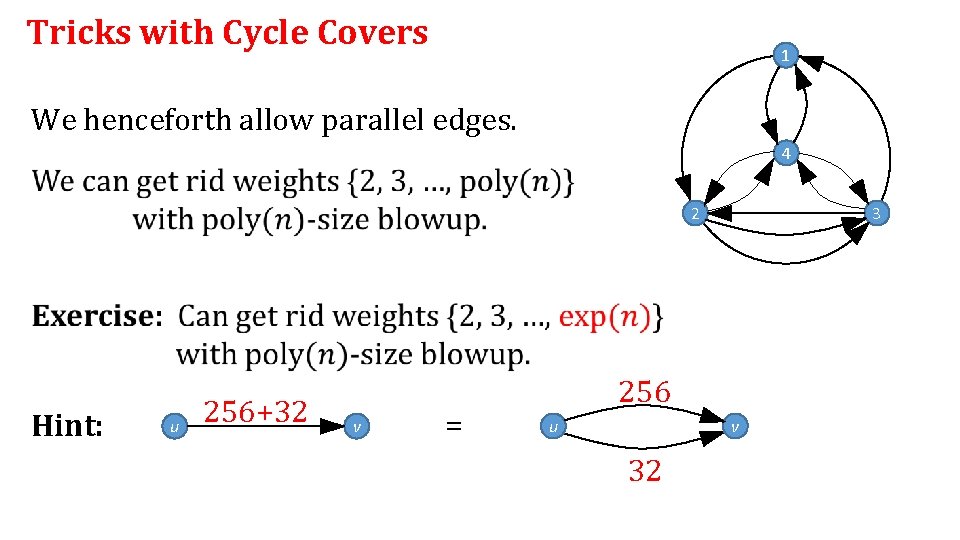
Tricks with Cycle Covers 1 We henceforth allow parallel edges. 4 2 3 Hint: u 256+32 v = 256 u v 32

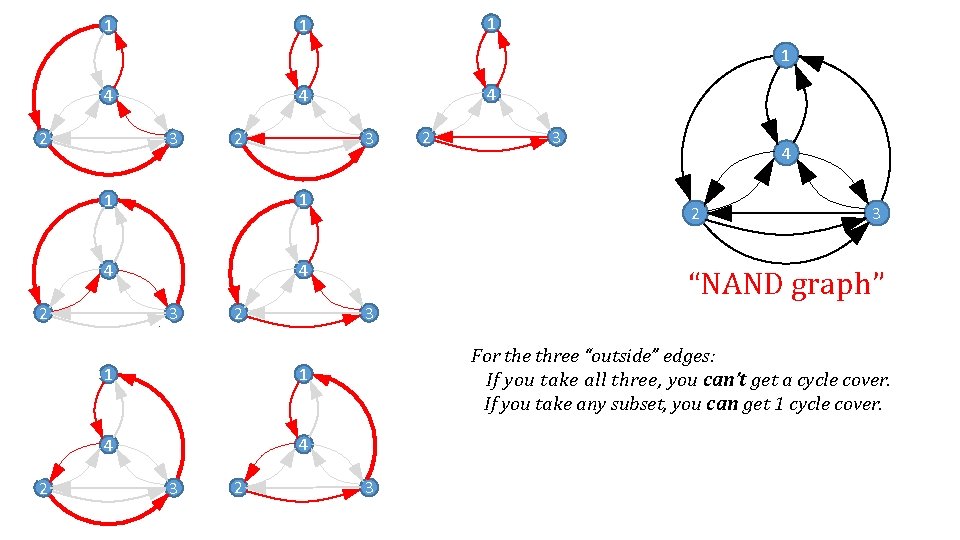
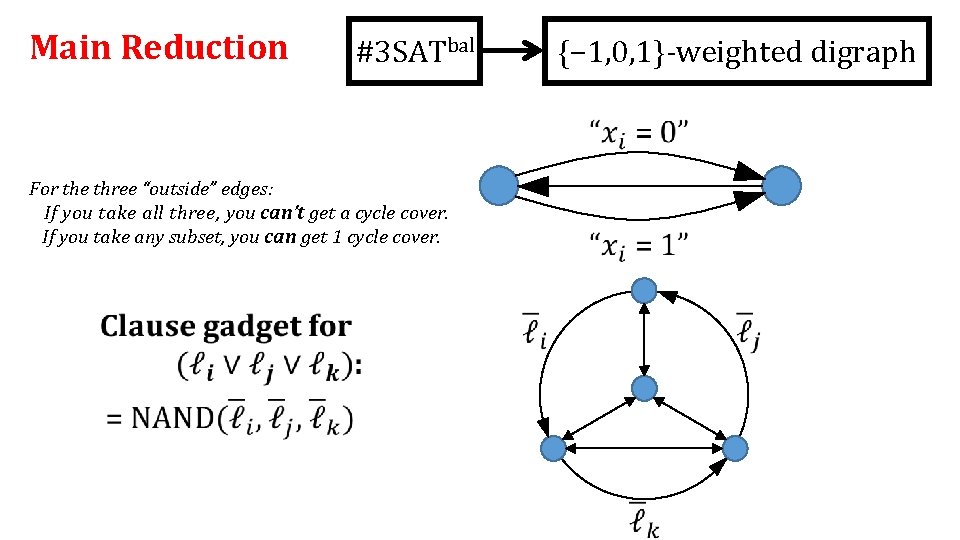
1 By the way… 4 2 3 “NAND graph” Key property: For the three “outside” edges: If you take all three, you can’t get a cycle cover. If you take any subset, you can get 1 cycle cover.

1 1 4 2 3 2 2 3 1 1 4 4 2 4 4 3 2 1 4 4 2 3 “NAND graph” 3 1 3 2 For the three “outside” edges: If you take all three, you can’t get a cycle cover. If you take any subset, you can get 1 cycle cover. 3

(trivial) #3 SATbal : ✔ (main) Per{− 1, 0, 1} ✔ Per{0, 1, …, n} Per{0, 1}

✔ #3 SAT ✔ (main) #3 SATbal : Per{− 1, 0, 1} ✔ Per{0, 1, …, n} Per{0, 1}

✔ #3 SATbal : #3 SATbal → ✔ (main) Per{− 1, 0, 1} ✔ Per{0, 1, …, n} Per{0, 1}

(main reduction) #3 SATbal Per{− 1, 0, 1} #3 SATbal →

(main reduction) #3 SATbal {− 1, 0, 1}-weighted digraph #3 SATbal →

(main reduction) #3 SATbal {− 1, 0, 1}-weighted digraph #3 SATbal → There are many more cycle covers, but their total weight is zero!

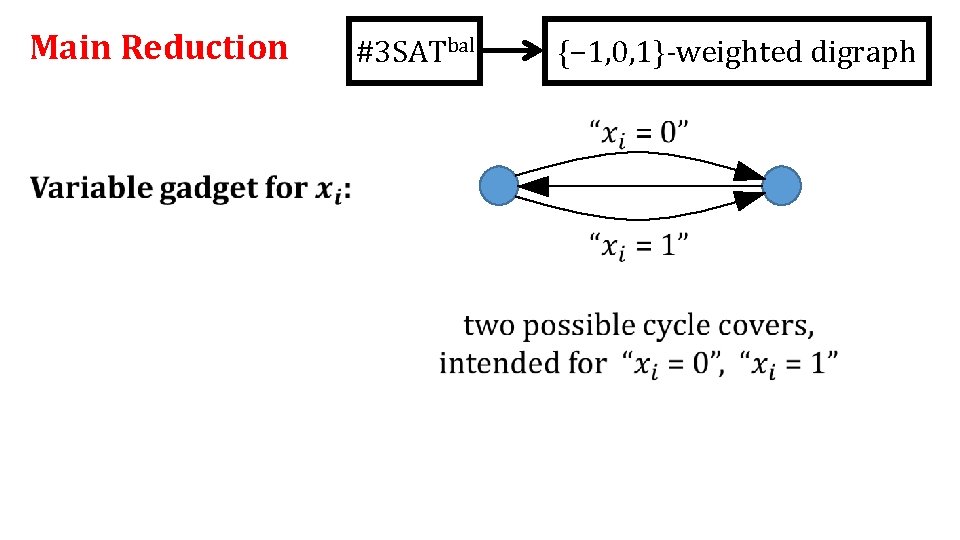
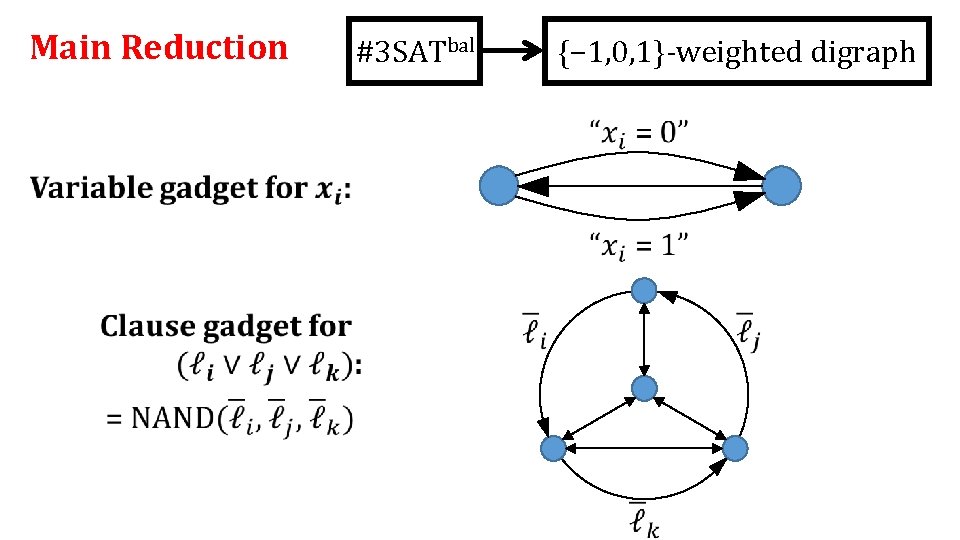
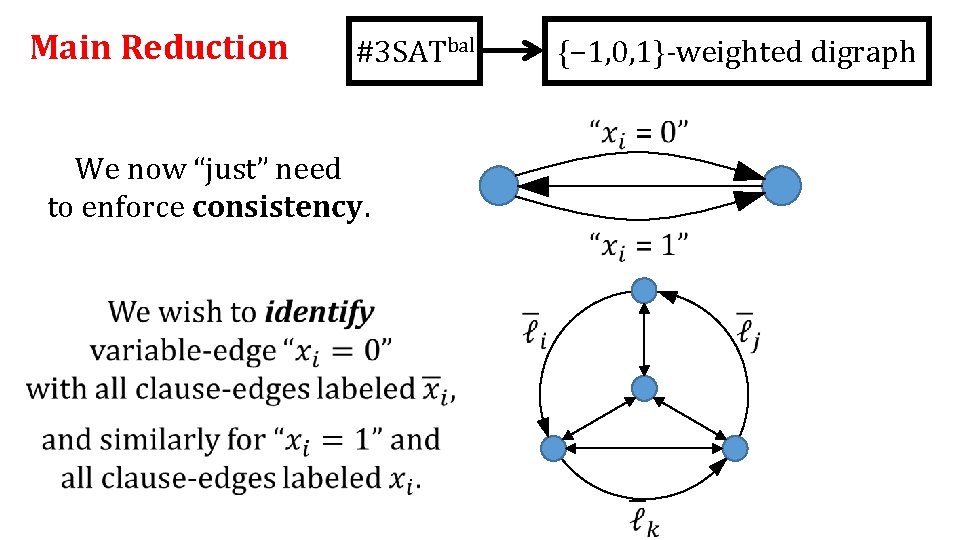
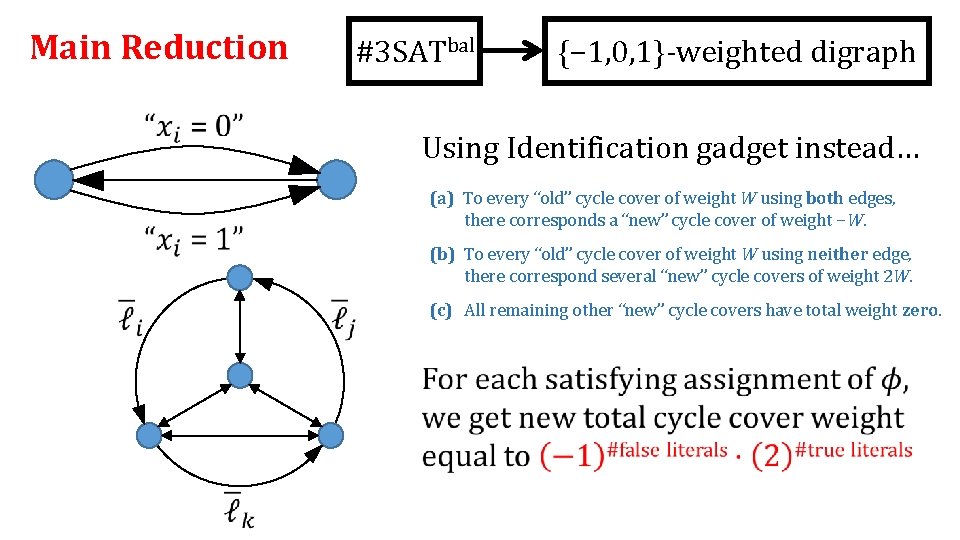
Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph For the three “outside” edges: If you take all three, you can’t get a cycle cover. If you take any subset, you can get 1 cycle cover.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph We now “just” need to enforce consistency.

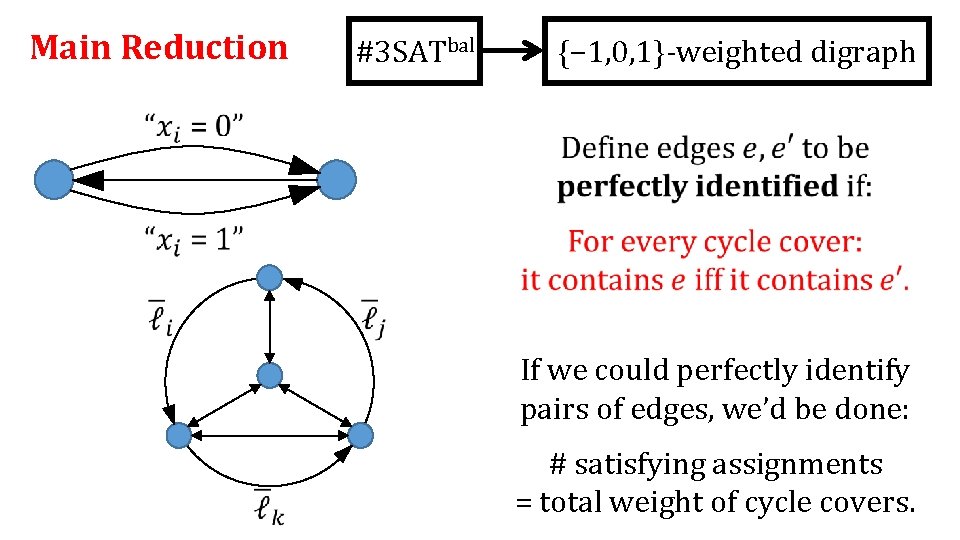
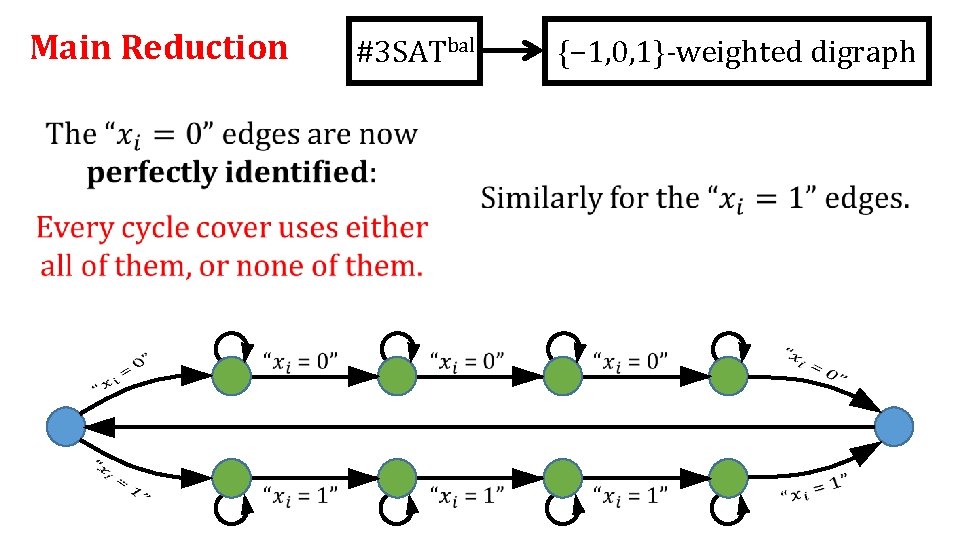
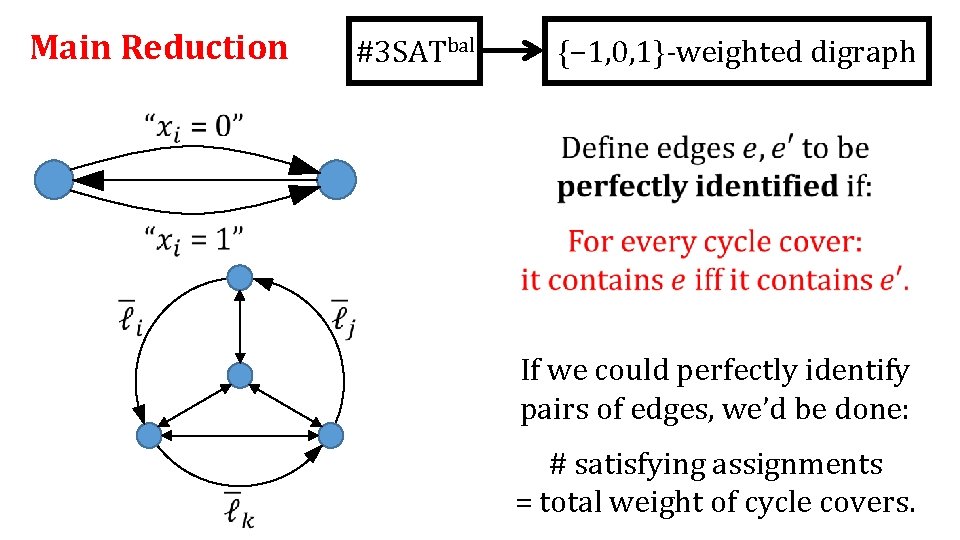
Main Reduction #3 SATbal We now “just” need to enforce consistency. {− 1, 0, 1}-weighted digraph If we could perfectly identify pairs of edges, we’d be done: # satisfying assignments = total weight of cycle covers.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph If we could perfectly identify pairs of edges, we’d be done: # satisfying assignments = total weight of cycle covers.

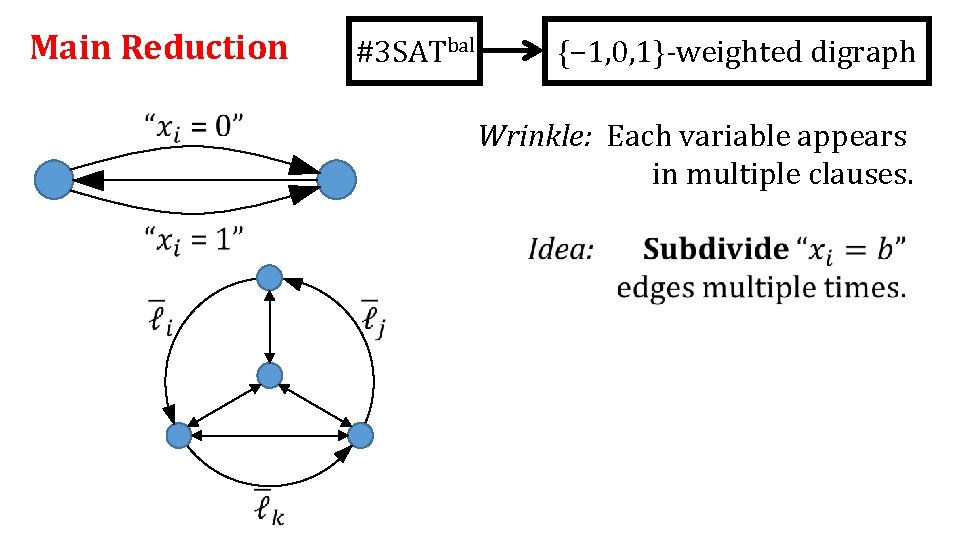
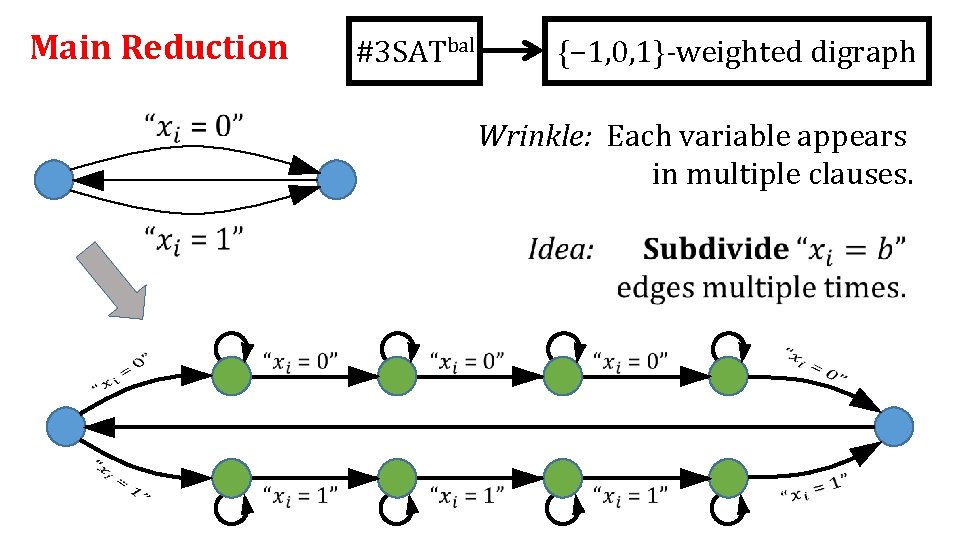
Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph Wrinkle: Each variable appears in multiple clauses.

Tricks with Cycle Covers 1 Trick 2: Can always subdivide any edge, sticking in a self-loop. Claim: Total cycle cover weight unchanged. 4 2 3 5

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph Wrinkle: Each variable appears in multiple clauses.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph Wrinkle: Each variable appears in multiple clauses.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph

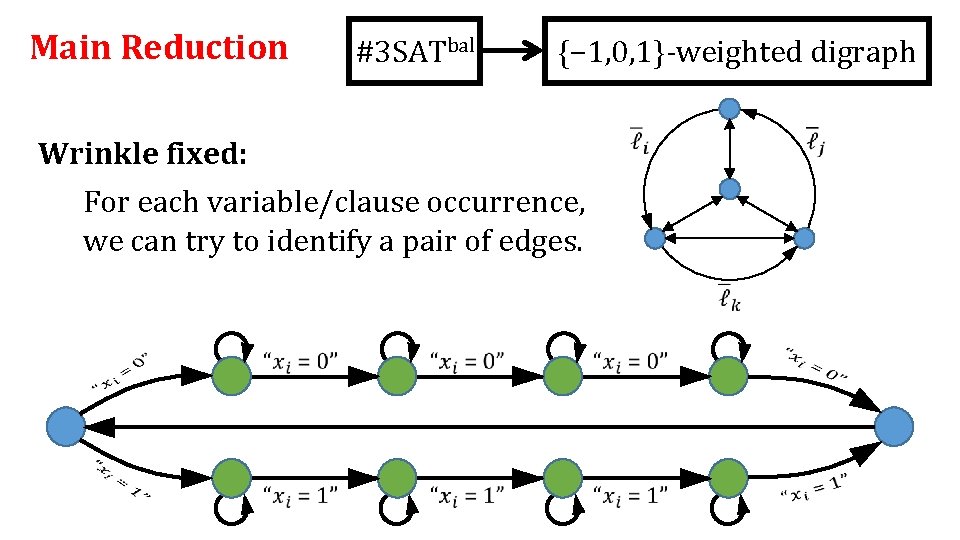
Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph Wrinkle fixed: For each variable/clause occurrence, we can try to identify a pair of edges.

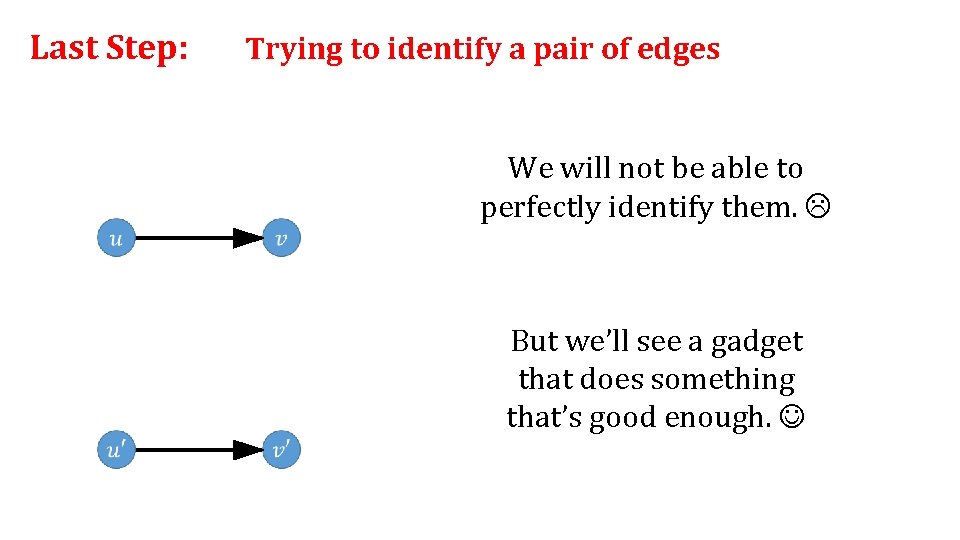
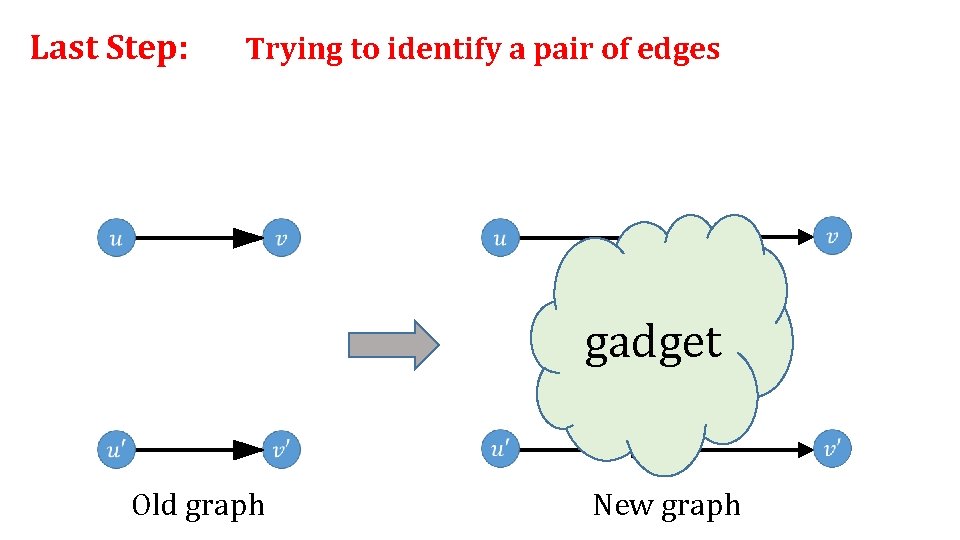
Last Step: Trying to identify a pair of edges We will not be able to perfectly identify them. But we’ll see a gadget that does something that’s good enough.

Last Step: Trying to identify a pair of edges gadget Old graph New graph

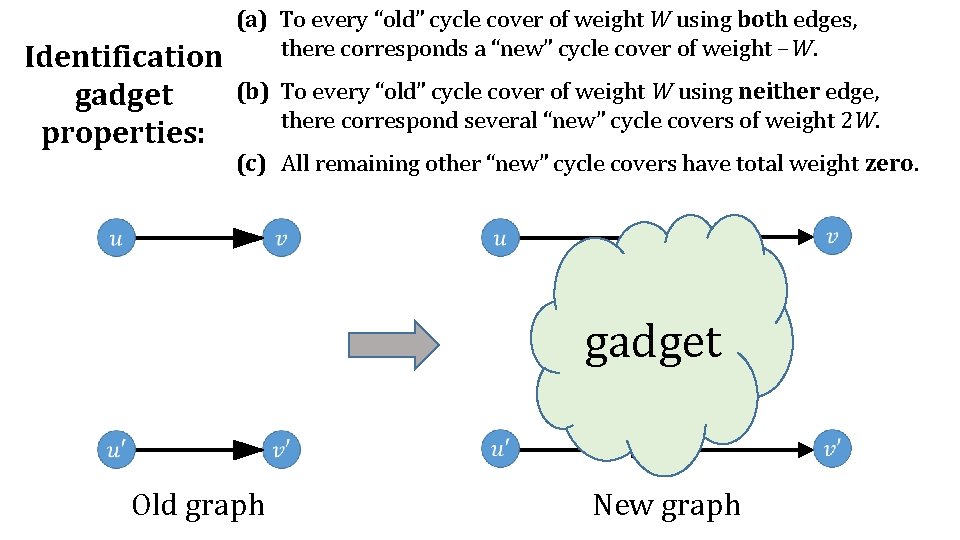
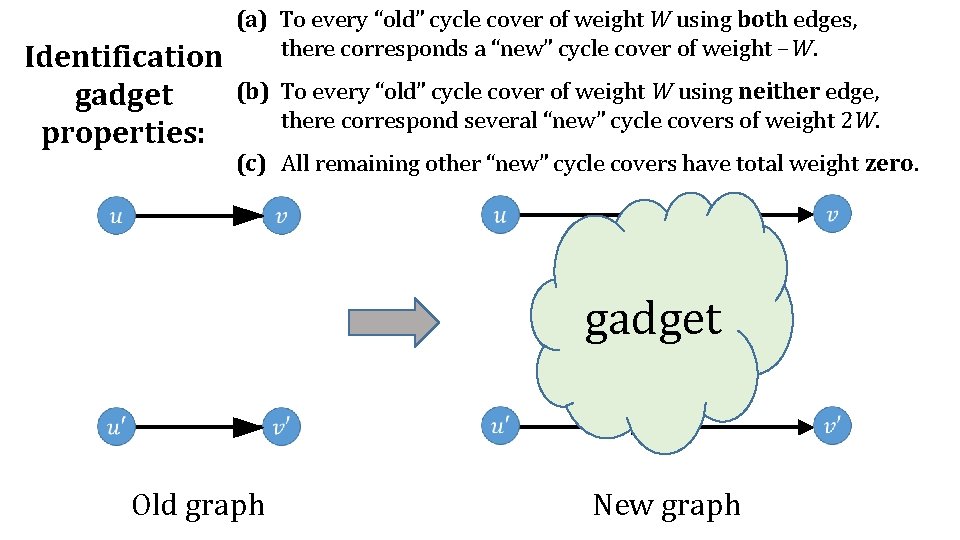
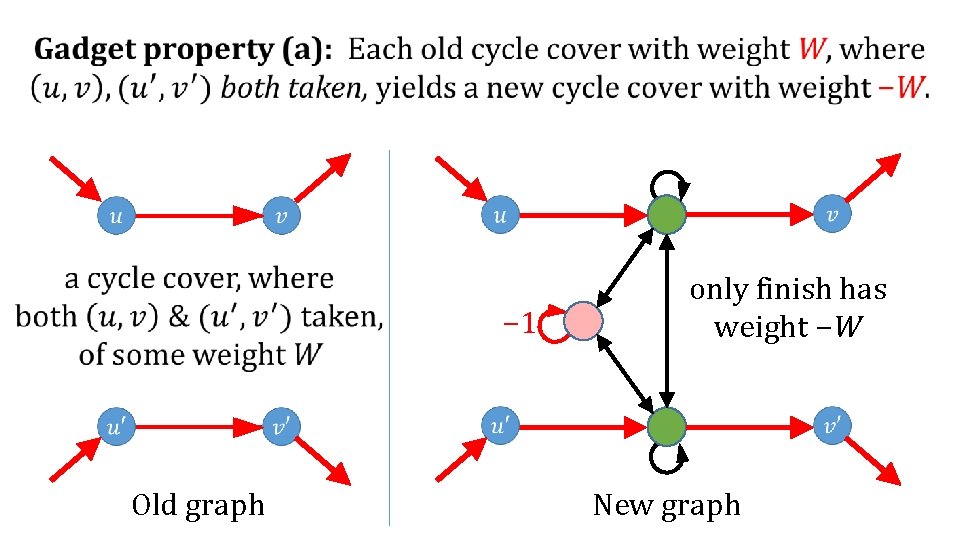
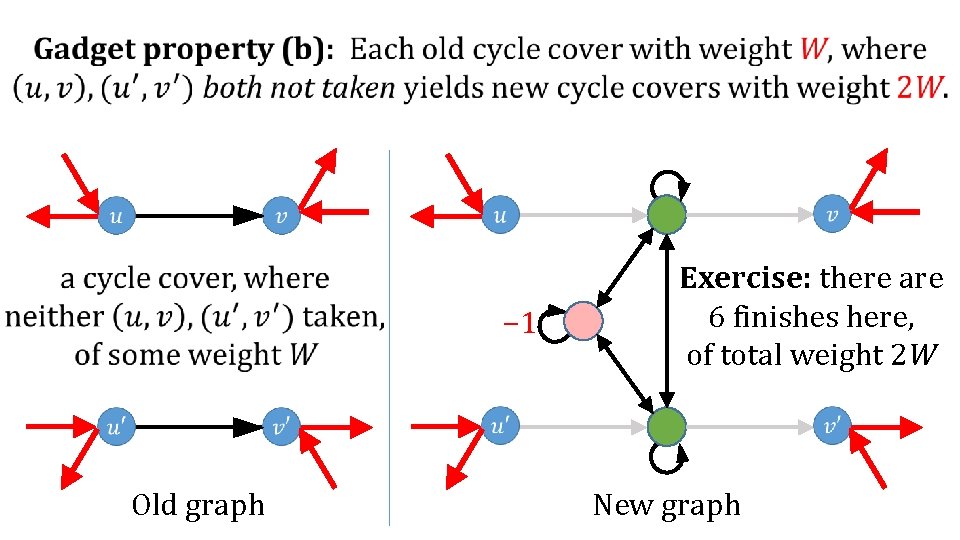
Identification gadget properties: (a) To every “old” cycle cover of weight W using both edges, there corresponds a “new” cycle cover of weight −W. (b) To every “old” cycle cover of weight W using neither edge, there correspond several “new” cycle covers of weight 2 W. (c) All remaining other “new” cycle covers have total weight zero. gadget Old graph New graph

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph We now “just” need to enforce consistency.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph If we could perfectly identify pairs of edges, we’d be done: # satisfying assignments = total weight of cycle covers.

Main Reduction #3 SATbal {− 1, 0, 1}-weighted digraph Using Identification gadget instead… (a) To every “old” cycle cover of weight W using both edges, there corresponds a “new” cycle cover of weight −W. (b) To every “old” cycle cover of weight W using neither edge, there correspond several “new” cycle covers of weight 2 W. (c) All remaining other “new” cycle covers have total weight zero.

Thus the Identification gadget completes the reduction! #3 SATbal {− 1, 0, 1}-weighted digraph #3 SATbal →

Identification gadget properties: (a) To every “old” cycle cover of weight W using both edges, there corresponds a “new” cycle cover of weight −W. (b) To every “old” cycle cover of weight W using neither edge, there correspond several “new” cycle covers of weight 2 W. (c) All remaining other “new” cycle covers have total weight zero. gadget Old graph New graph

Identification gadget revealed gadget Old graph New graph

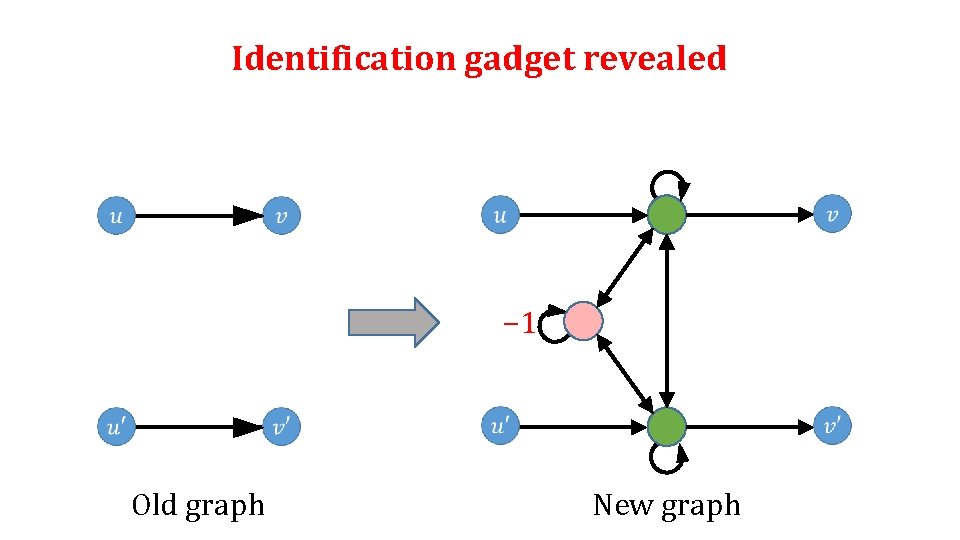
Identification gadget revealed − 1 Old graph New graph

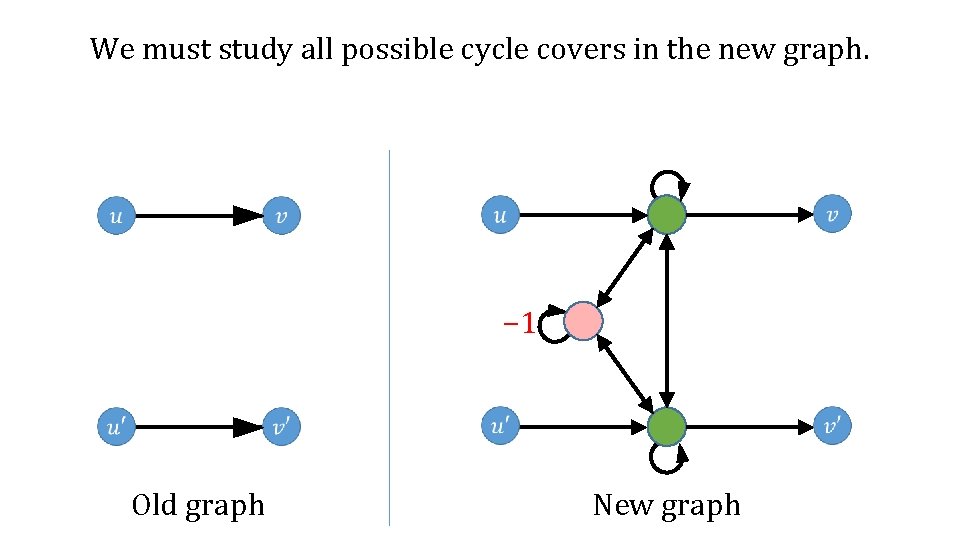
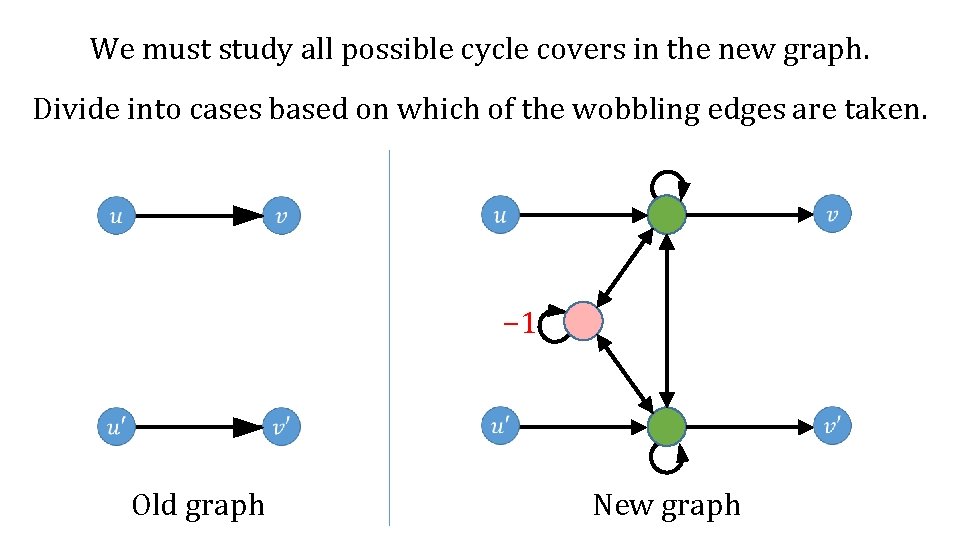
We must study all possible cycle covers in the new graph. − 1 Old graph New graph

We must study all possible cycle covers in the new graph. Divide into cases based on which of the wobbling edges are taken. − 1 Old graph New graph

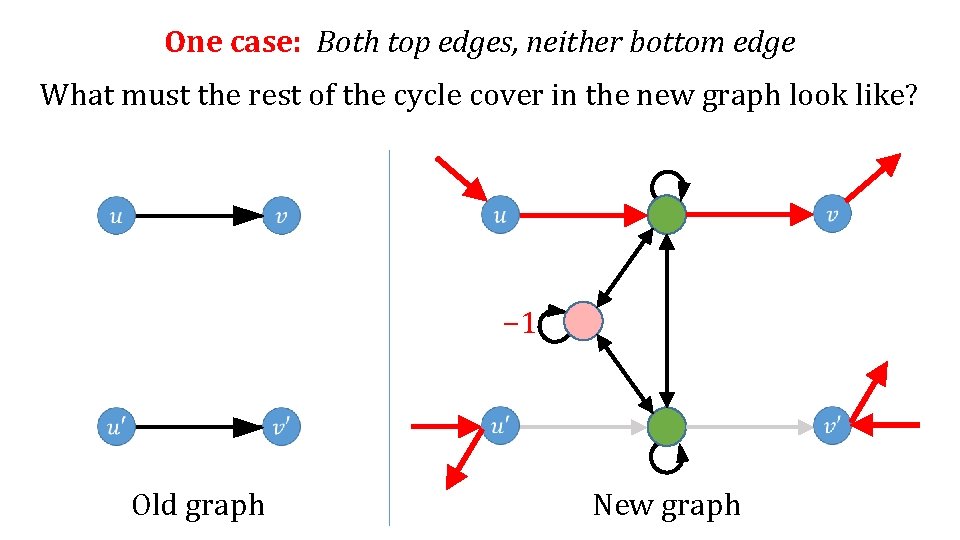
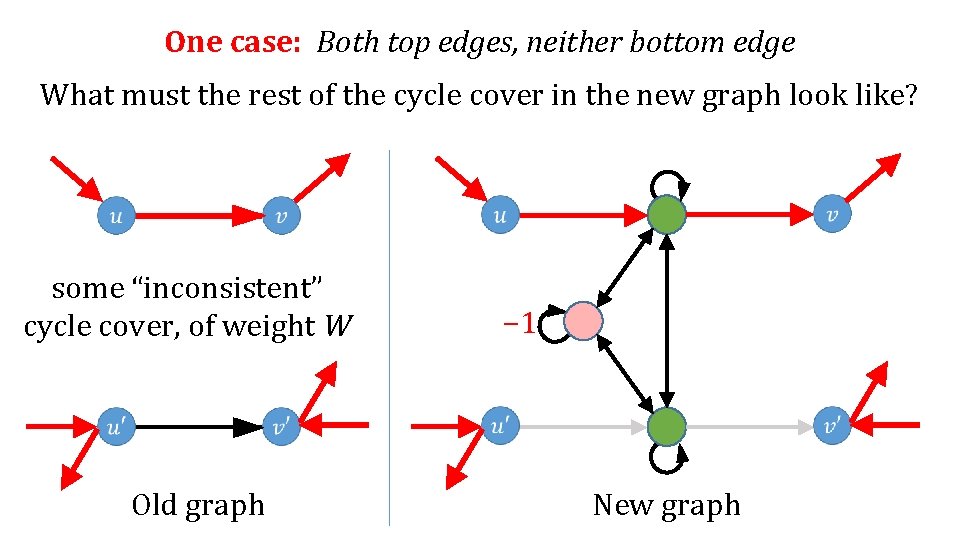
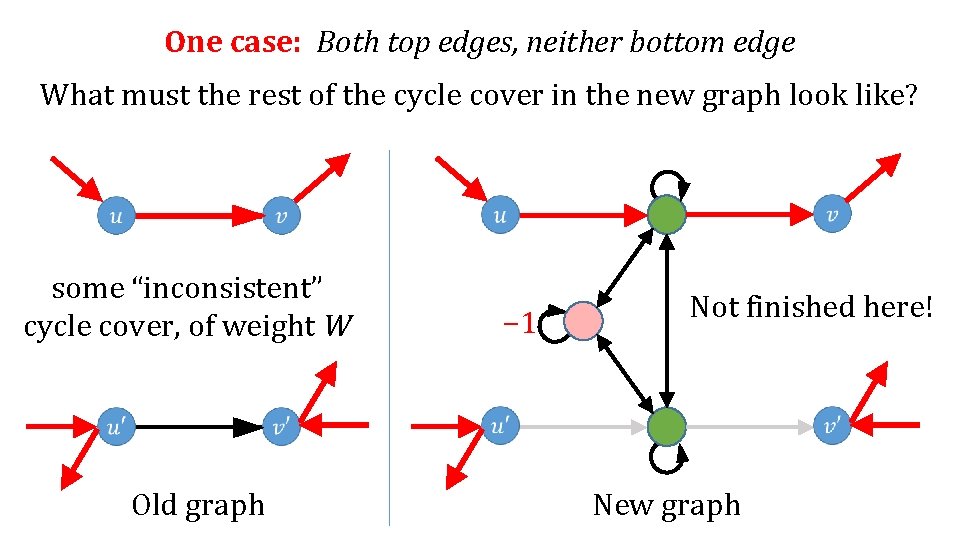
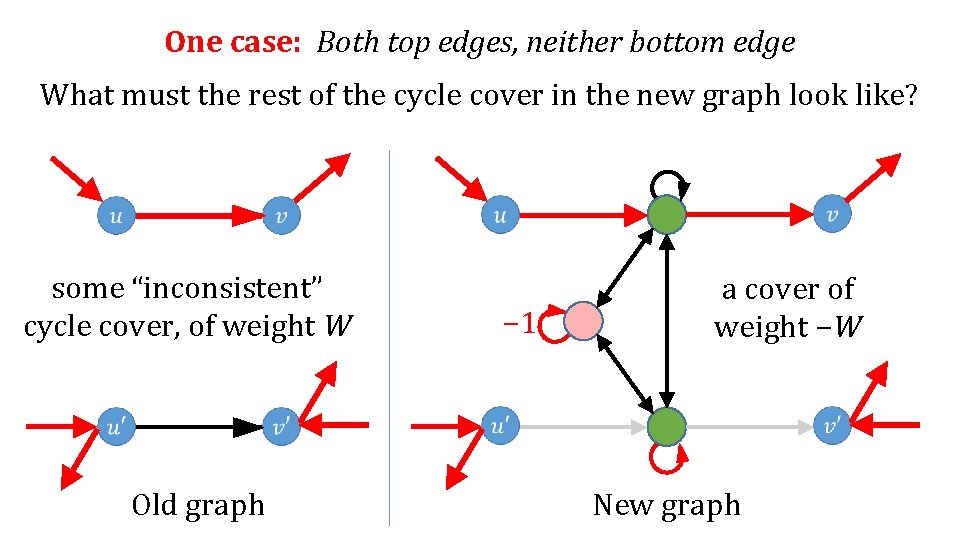
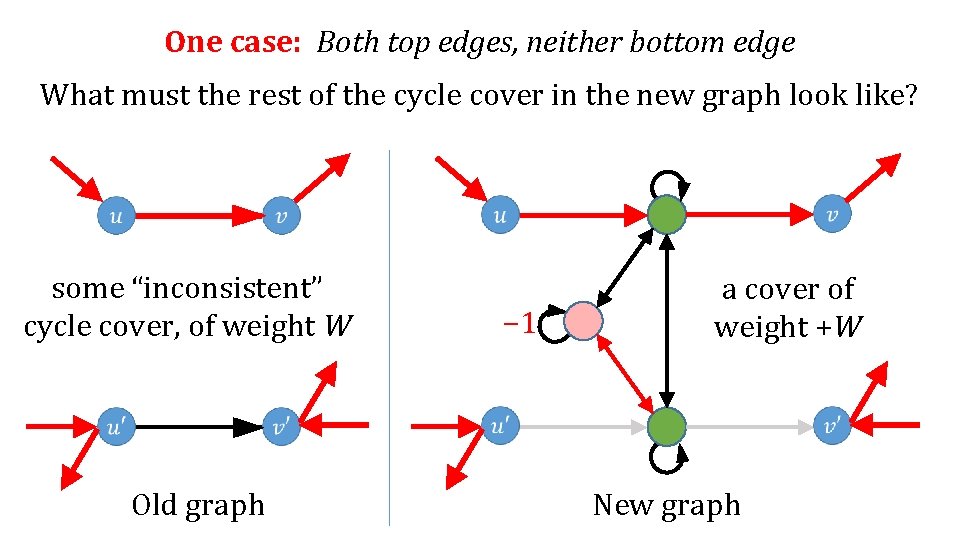
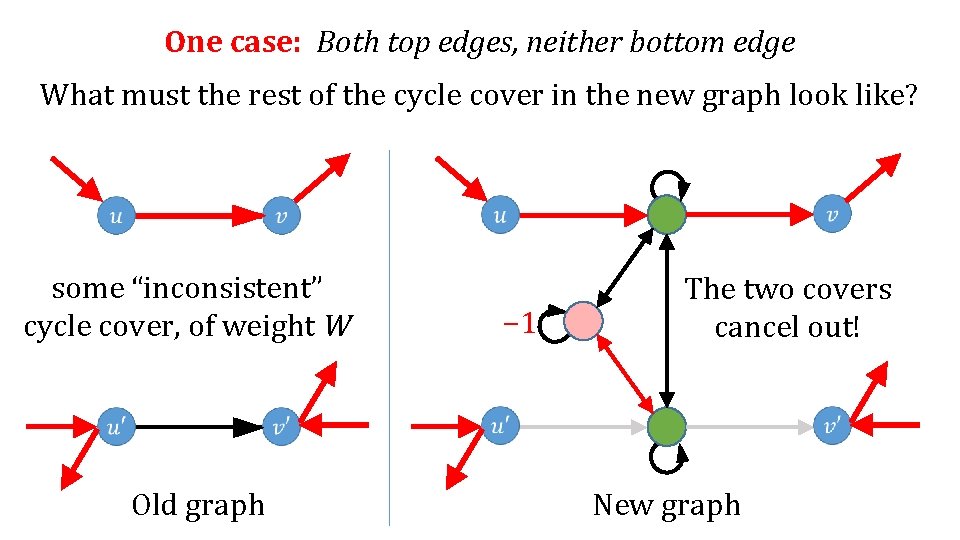
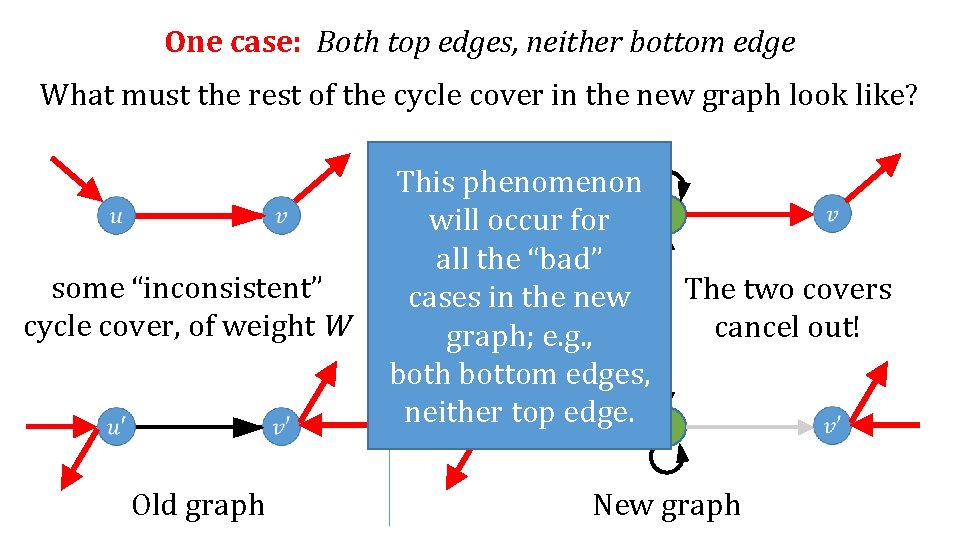
One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? − 1 Old graph New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph − 1 New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph − 1 Not finished here! New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph − 1 a cover of weight −W New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph − 1 a cover of weight +W New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph − 1 The two covers cancel out! New graph

One case: Both top edges, neither bottom edge What must the rest of the cycle cover in the new graph look like? some “inconsistent” cycle cover, of weight W Old graph This phenomenon will occur for all the “bad” cases in the new − 1 e. g. , graph; both bottom edges, neither top edge. The two covers cancel out! New graph

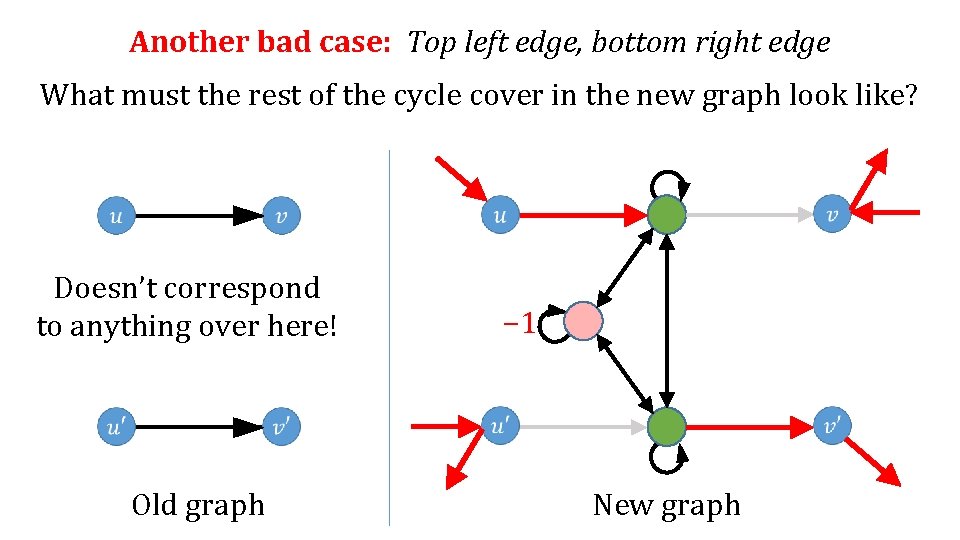
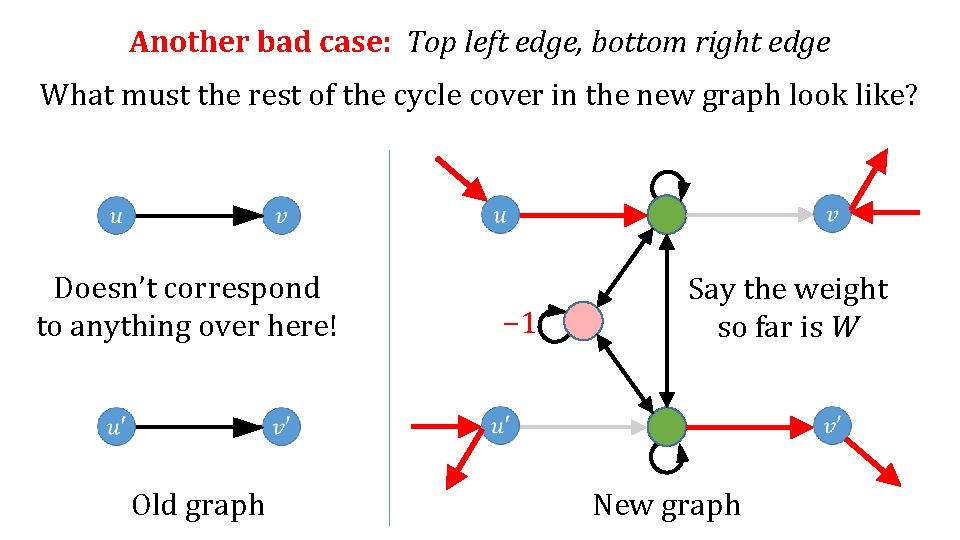
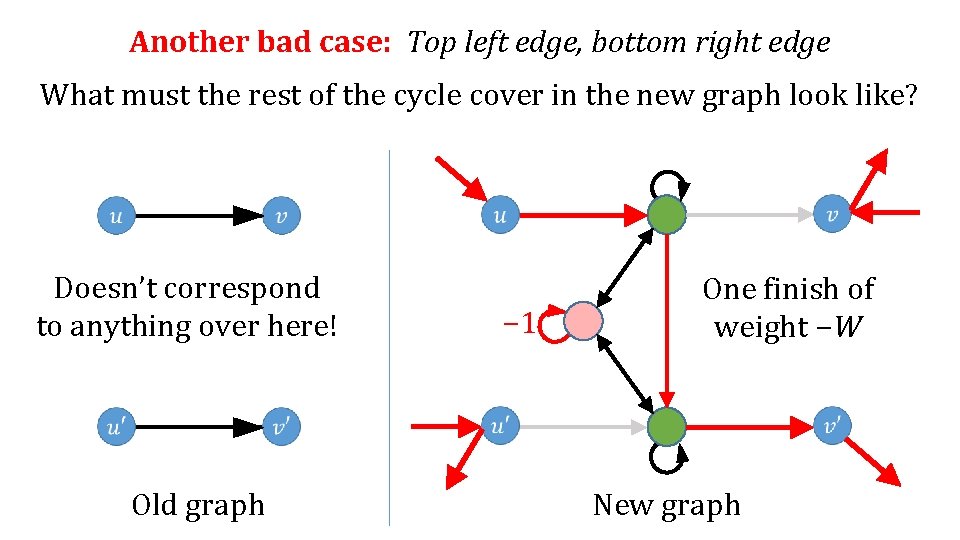
Another bad case: Top left edge, bottom right edge What must the rest of the cycle cover in the new graph look like? Doesn’t correspond to anything over here! Old graph − 1 New graph

Another bad case: Top left edge, bottom right edge What must the rest of the cycle cover in the new graph look like? Doesn’t correspond to anything over here! Old graph − 1 Say the weight so far is W New graph

Another bad case: Top left edge, bottom right edge What must the rest of the cycle cover in the new graph look like? Doesn’t correspond to anything over here! Old graph − 1 One finish of weight −W New graph

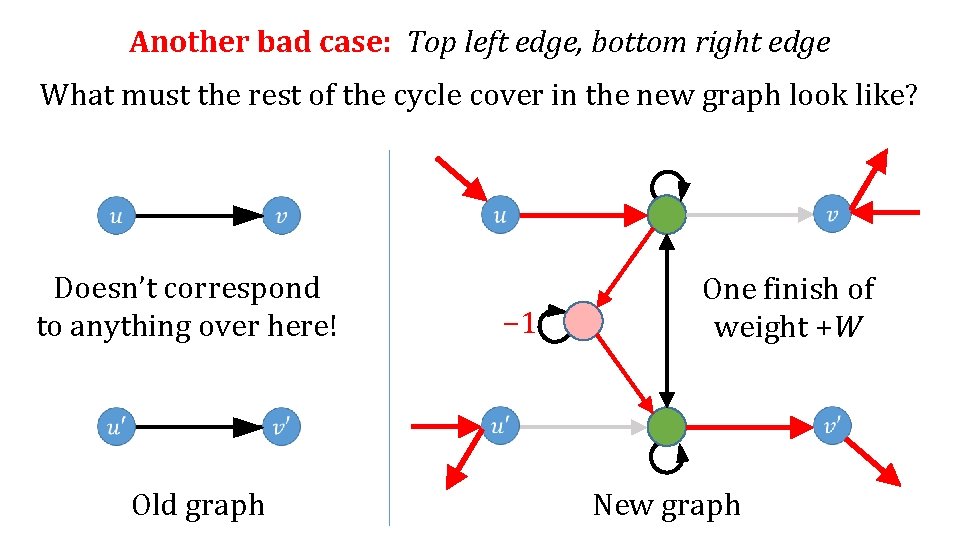
Another bad case: Top left edge, bottom right edge What must the rest of the cycle cover in the new graph look like? Doesn’t correspond to anything over here! Old graph − 1 One finish of weight +W New graph

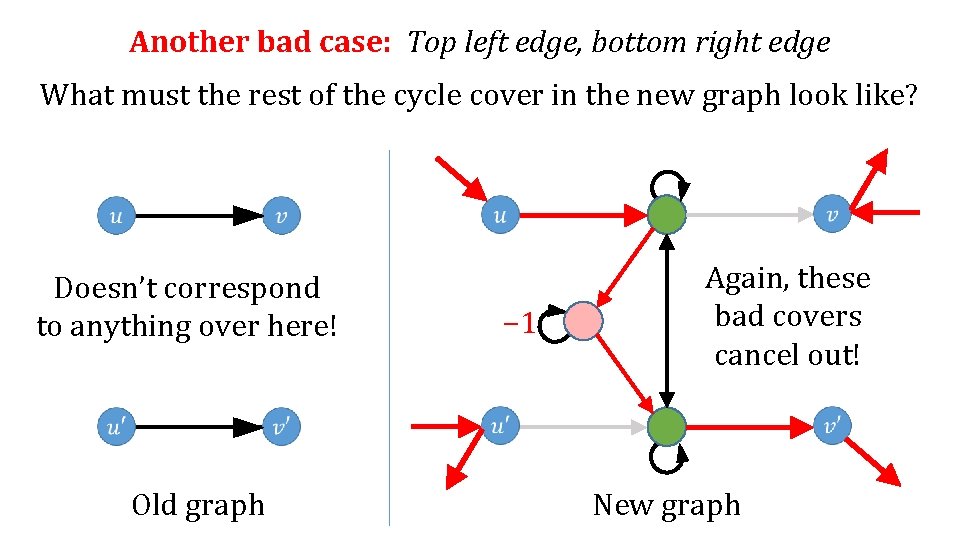
Another bad case: Top left edge, bottom right edge What must the rest of the cycle cover in the new graph look like? Doesn’t correspond to anything over here! Old graph − 1 Again, these bad covers cancel out! New graph

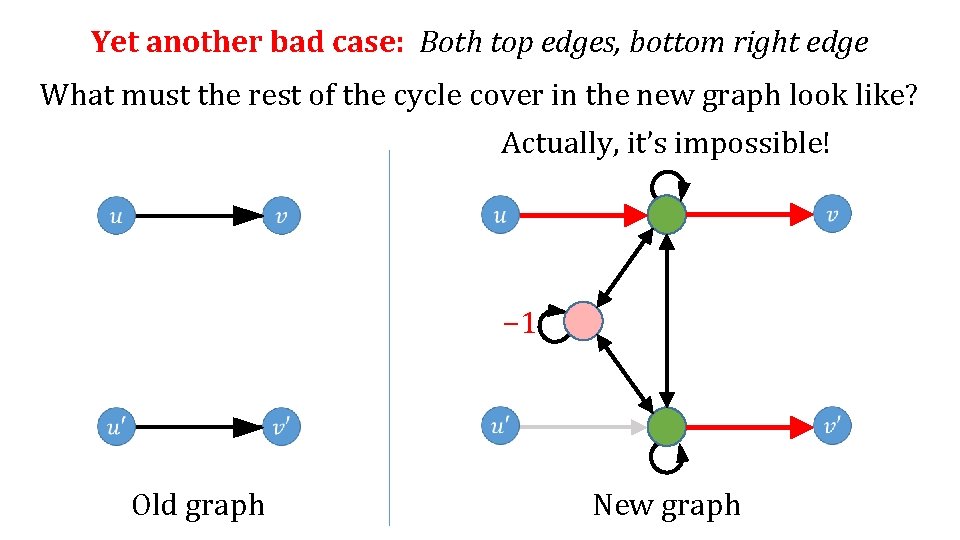
Yet another bad case: Both top edges, bottom right edge What must the rest of the cycle cover in the new graph look like? Actually, it’s impossible! − 1 Old graph New graph

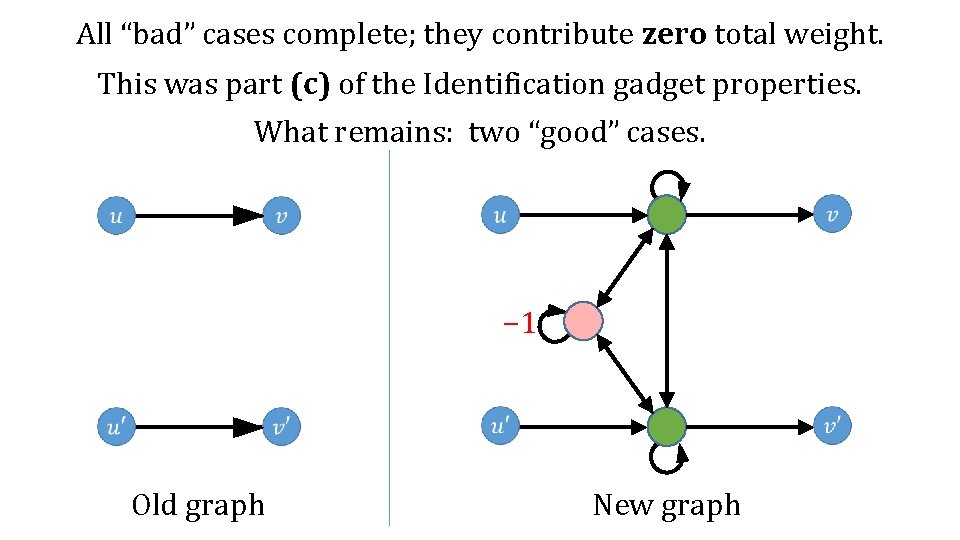
All “bad” cases complete; they contribute zero total weight. This was part (c) of the Identification gadget properties. What remains: two “good” cases. − 1 Old graph New graph

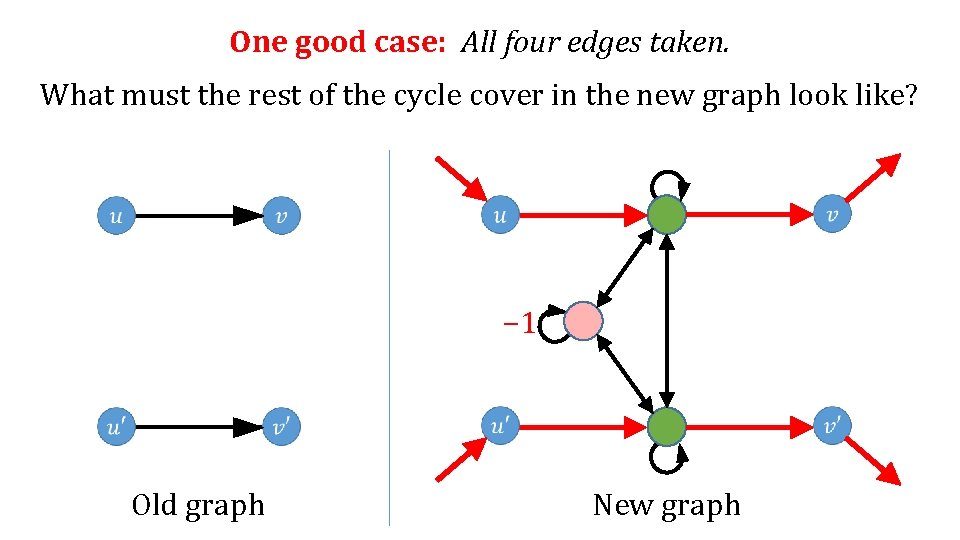
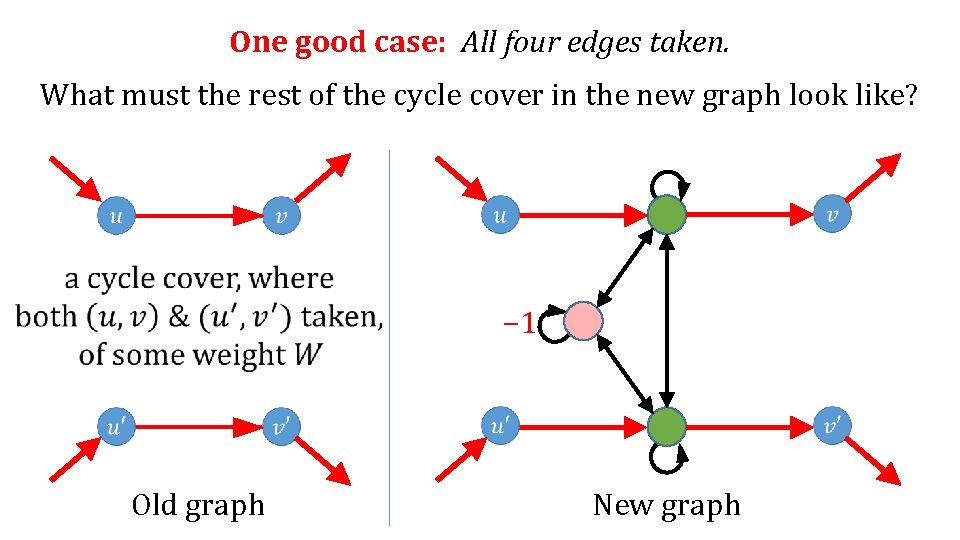
One good case: All four edges taken. What must the rest of the cycle cover in the new graph look like? − 1 Old graph New graph

One good case: All four edges taken. What must the rest of the cycle cover in the new graph look like? − 1 Old graph New graph

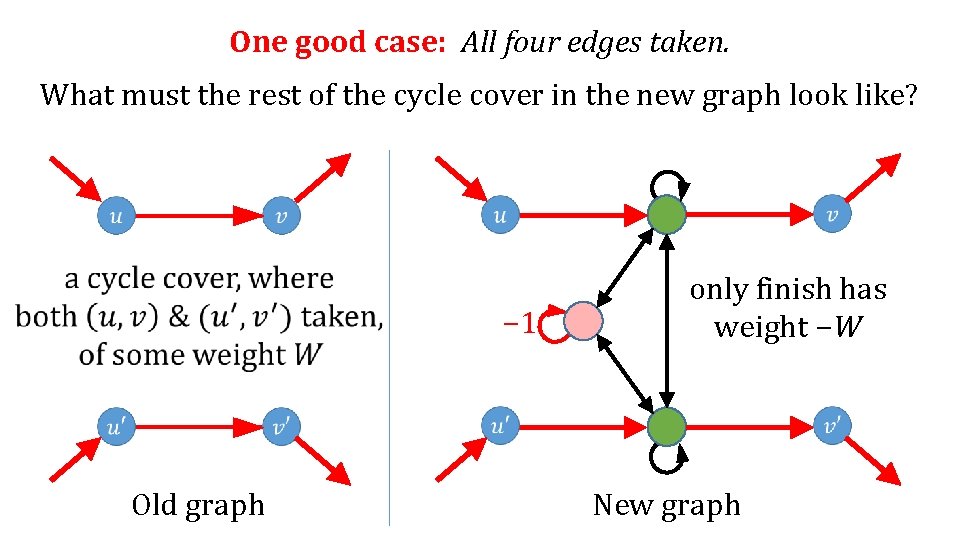
One good case: All four edges taken. What must the rest of the cycle cover in the new graph look like? − 1 Old graph only finish has weight −W New graph

− 1 Old graph only finish has weight −W New graph

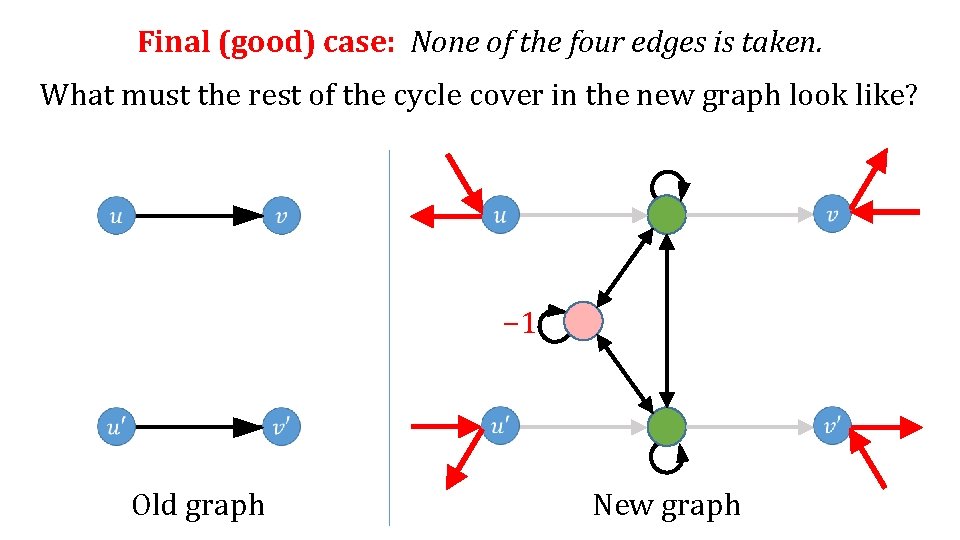
Final (good) case: None of the four edges is taken. What must the rest of the cycle cover in the new graph look like? − 1 Old graph New graph

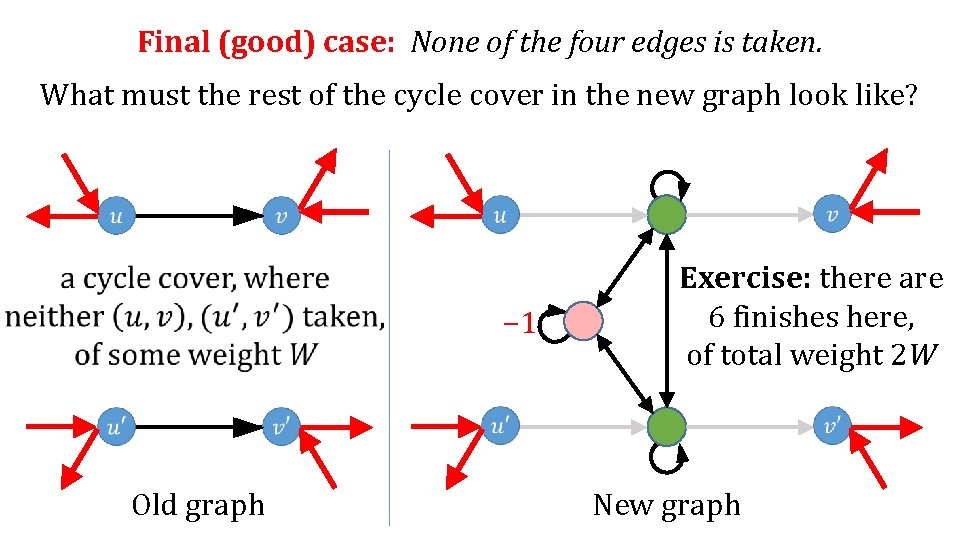
Final (good) case: None of the four edges is taken. What must the rest of the cycle cover in the new graph look like? − 1 Old graph Exercise: there are 6 finishes here, of total weight 2 W New graph

− 1 Old graph Exercise: there are 6 finishes here, of total weight 2 W New graph

Identification gadget properties: (a) To every “old” cycle cover of weight W using both edges, there corresponds a “new” cycle cover of weight −W. (b) To every “old” cycle cover of weight W using neither edge, there correspond several “new” cycle covers of weight 2 W. (c) All remaining other “new” cycle covers have total weight zero. All gadget properties verified! The reduction is complete.