CMSC 341 Lecture 21 Graphs Introduction Prof Neary

CMSC 341 Lecture 21 Graphs (Introduction) Prof. Neary Based on slides from previous iterations of this course (Dr. Katherine Gibson)

Basic Graph Definitions § A graph G = (V, E) consists of a finite set of vertices, V, and a finite set of edges, E. § Each edge is a pair (v, w) where v, w V q q q V and E are sets, so each vertex v V is unique, and each edge e E is unique. Edges are sometimes called arcs or lines Vertices are sometimes called nodes or points UMBC CMSC 341 Graphs (Introduction) 2

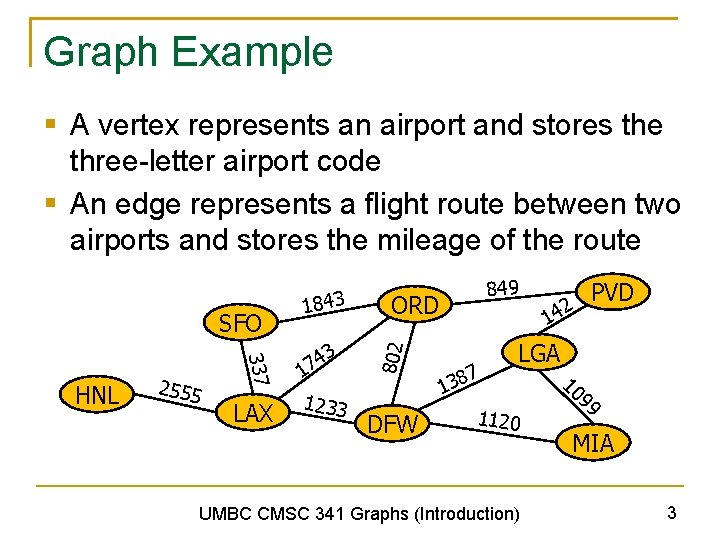
Graph Example § A vertex represents an airport and stores the three-letter airport code § An edge represents a flight route between two airports and stores the mileage of the route 337 HNL 2555 LAX 3 4 7 1 1233 849 ORD 802 SFO 1843 DFW PVD 42 1 7 138 LGA 1120 UMBC CMSC 341 Graphs (Introduction) 10 99 MIA 3

Graph Applications § Graphs can be used to model a wide range of applications including q q q Intersections and streets within a city Roads/trains/airline routes connecting cities/countries Computer networks Electronic circuits What else? UMBC CMSC 341 Graphs (Introduction) 4

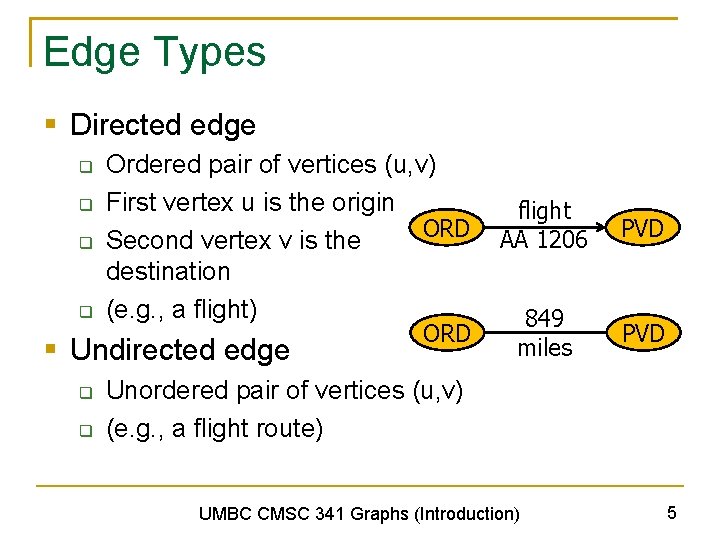
Edge Types § Directed edge q q Ordered pair of vertices (u, v) First vertex u is the origin ORD Second vertex v is the destination (e. g. , a flight) § Undirected edge q q ORD flight AA 1206 PVD 849 miles PVD Unordered pair of vertices (u, v) (e. g. , a flight route) UMBC CMSC 341 Graphs (Introduction) 5

Graph Types § Directed graph q q q All the edges are directed (edges are ordered pairs) (e. g. , route network) Sometimes called a digraph § Undirected graph q q All the edges are undirected (unordered pairs) (e. g. , flight network) § Sparse and dense graphs q “Few” and “many” edges, respectively UMBC CMSC 341 Graphs (Introduction) 6

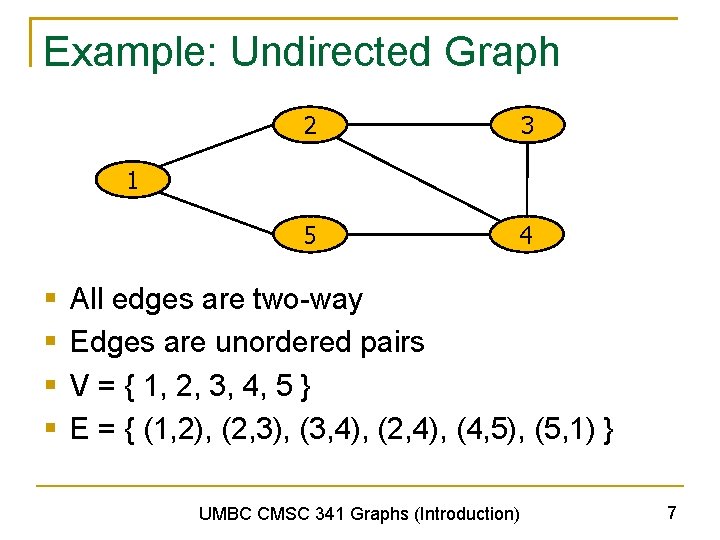
Example: Undirected Graph 2 3 5 4 1 § § All edges are two-way Edges are unordered pairs V = { 1, 2, 3, 4, 5 } E = { (1, 2), (2, 3), (3, 4), (2, 4), (4, 5), (5, 1) } UMBC CMSC 341 Graphs (Introduction) 7

Example: Directed Graph 2 3 5 4 1 § § All edges are “one-way” (as shown by arrows) Edges are ordered pairs V = { 1, 2, 3, 4, 5 } E = { (1, 2), (3, 2), (4, 3), (2, 4), (4, 5), (5, 1), (5, 4) } UMBC CMSC 341 Graphs (Introduction) 8

Graph Terminology and Vocabulary

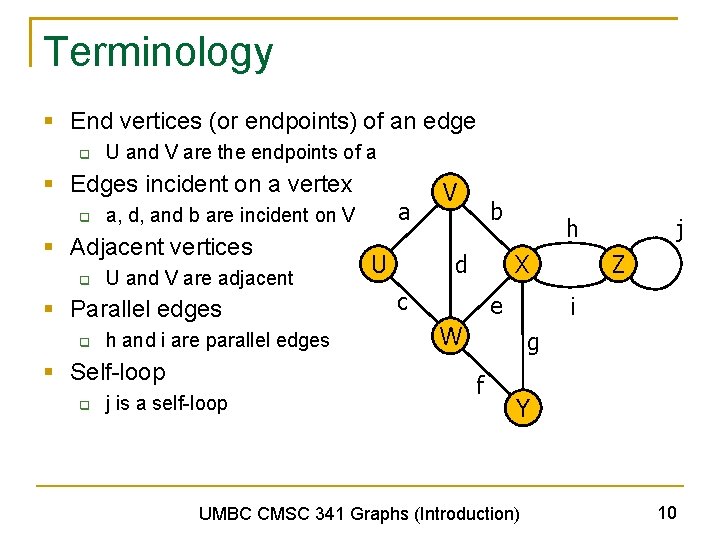
Terminology § End vertices (or endpoints) of an edge q U and V are the endpoints of a § Edges incident on a vertex q § Adjacent vertices q U and V are adjacent § Parallel edges q h and i are parallel edges § Self-loop q a a, d, and b are incident on V j is a self-loop U V b h X d c e j Z i W g f Y UMBC CMSC 341 Graphs (Introduction) 10

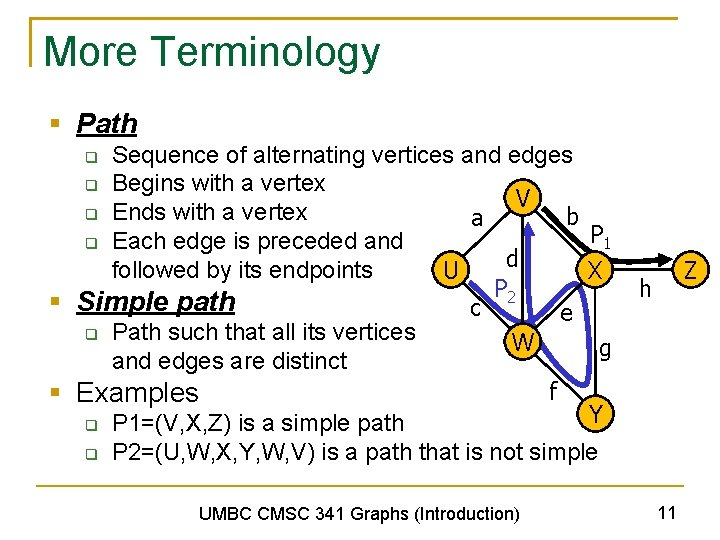
More Terminology § Path Sequence of alternating vertices and edges q Begins with a vertex V q Ends with a vertex b a P 1 q Each edge is preceded and d followed by its endpoints U X P 2 § Simple path c e q Path such that all its vertices W g and edges are distinct f § Examples Y q P 1=(V, X, Z) is a simple path q P 2=(U, W, X, Y, W, V) is a path that is not simple q UMBC CMSC 341 Graphs (Introduction) Z h 11

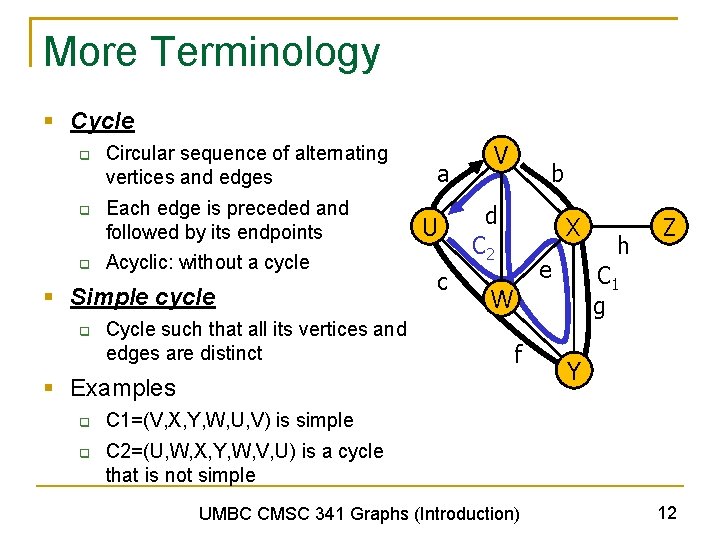
More Terminology § Cycle q q q Circular sequence of alternating vertices and edges Each edge is preceded and followed by its endpoints Acyclic: without a cycle § Simple cycle q Cycle such that all its vertices and edges are distinct a U c V b d C 2 X e § Examples q q C 1 g W f h Z Y C 1=(V, X, Y, W, U, V) is simple C 2=(U, W, X, Y, W, V, U) is a cycle that is not simple UMBC CMSC 341 Graphs (Introduction) 12

Vocabulary § Vertex w is adjacent to vertex v if and only if (v, w) E. § For undirected graphs, with edge (v, w), and hence also (w, v), w is adjacent to v and v is adjacent to w. § An edge may also have: q q Weight or cost -- an associated value Label -- a unique name § The degree of a vertex, v, is the number of vertices adjacent to v. Degree is also called valence. UMBC CMSC 341 Graphs (Introduction) 13

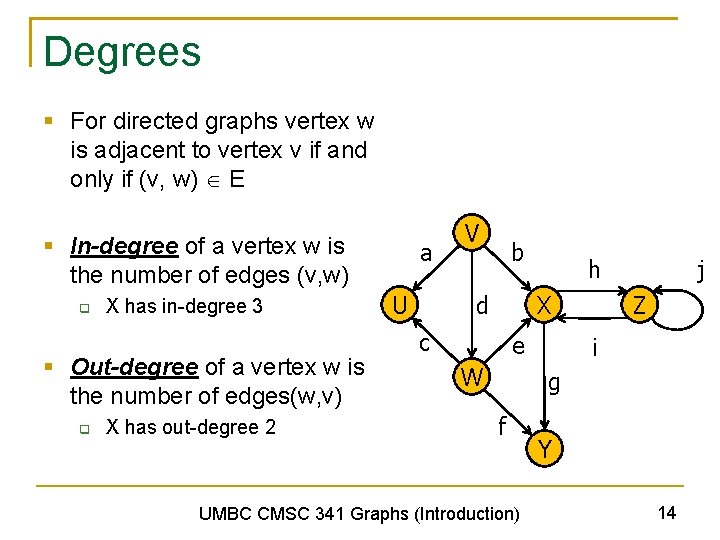
Degrees § For directed graphs vertex w is adjacent to vertex v if and only if (v, w) E § In-degree of a vertex w is the number of edges (v, w) q X has in-degree 3 § Out-degree of a vertex w is the number of edges(w, v) q X has out-degree 2 a U V b h X d c e W j Z i g f UMBC CMSC 341 Graphs (Introduction) Y 14

Connectedness § An undirected graph is connected if there is a path from every vertex to every other vertex § A directed graph is strongly connected if there is a path from every vertex to every other vertex § A directed graph is weakly connected if there would be a path from every vertex to every other vertex, disregarding the direction of the edges § A complete graph is one in which there is an edge between every pair of vertices § A connected component of a graph is any maximal connected subgraph. Connected components are sometimes simply called components UMBC CMSC 341 Graphs (Introduction) 15

Graph Algorithms § Graph Traversal q q q Breadth First Search (BFS) Depth First Search (DFS) Uniform Cost Search (UCS) A/A* Search Etc. . . § Shortest Paths q q q Bellman-Ford Dijsktra’s Floyd-Warshall UMBC CMSC 341 Graphs (Introduction) 16

Graph Traversal § Depth First Search (DFS) § DFS(v): q q Mark v as ”visited” For each edge v -> u: § DFS(u) § (could use a stack instead of recursion) UMBC CMSC 341 Graphs (Introduction) 17

Graph Traversal § Breadth First Search q BFS(v): § Initialize a queue Q § Mark v as visited, and enqueue v § While Q is not empty: q q w = Q. dequeue() For each edge w -> u: § If u is not visited, mark it as visited and enqueue it UMBC CMSC 341 Graphs (Introduction) 18

A Graph ADT § Has some data elements q Vertices and Edges § Has some operations q q q get. Degree( u ) -- Returns the degree of vertex u (outdegree of vertex u in directed graph) get. Adjacent( u ) -- Returns a list of the vertices adjacent to vertex u (list of vertices that u points to for a directed graph) is. Adjacent. To( u, v ) -- Returns TRUE if vertex v is adjacent to vertex u, FALSE otherwise. § Has some associated algorithms to be discussed. 8/3/2007 UMBC CMSC 341 Graphs 19

Adjacency Matrix Implementation § Uses array of size |V| where each entry (i , j) is boolean q TRUE if there is an edge from vertex i to vertex j q FALSE otherwise q store weights when edges are weighted § Very simple, but large space requirement = O(|V|2) § Appropriate if the graph is dense. § Otherwise, most of the entries in the table are FALSE. § For example, if a graph is used to represent a street map like Manhattan in which most streets run E/W or N/S, each intersection is attached to only 4 streets and |E| < 4*|V|. If there are 3000 intersections, the table has 9, 000 entries of which only 12, 000 are TRUE. 8/3/2007 UMBC CMSC 341 Graphs 20

Undirected Graph / Adjacency Matrix 1 2 5 3 4 8/3/2007 UMBC CMSC 341 Graphs 21

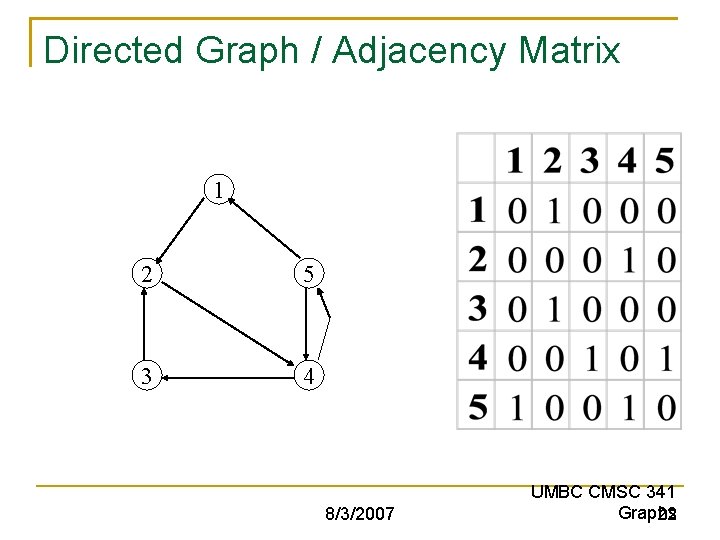
Directed Graph / Adjacency Matrix 1 2 5 3 4 8/3/2007 UMBC CMSC 341 Graphs 22

Weighted, Directed Graph / Adjacency Matrix 1 8 2 2 5 6 5 7 2 3 3 4 8/3/2007 UMBC CMSC 341 Graphs 23

Adjacency Matrix Performance Storage requirement: O(|V|2 ) Performance: get. Degree ( u ) O(|V|) is. Adjacent. To( u, v ) O(1) get. Adjacent( u ) O(|V|) 8/3/2007 UMBC CMSC 341 Graphs 24

Adjacency List Implementation § If the graph is sparse, then keeping a list of adjacent vertices for each vertex saves space. Adjacency Lists are the commonly used representation. The lists may be stored in a data structure or in the Vertex object itself. q Vector of lists: A vector of lists of vertices. The ith element of the vector is a list, Li, of the vertices adjacent to vi. § If the graph is sparse, then the space requirement is O( |E| + |V| ), “linear in the size of the graph” § If the graph is dense, then the space requirement is O( |V|2 ) 8/3/2007 UMBC CMSC 341 Graphs 25

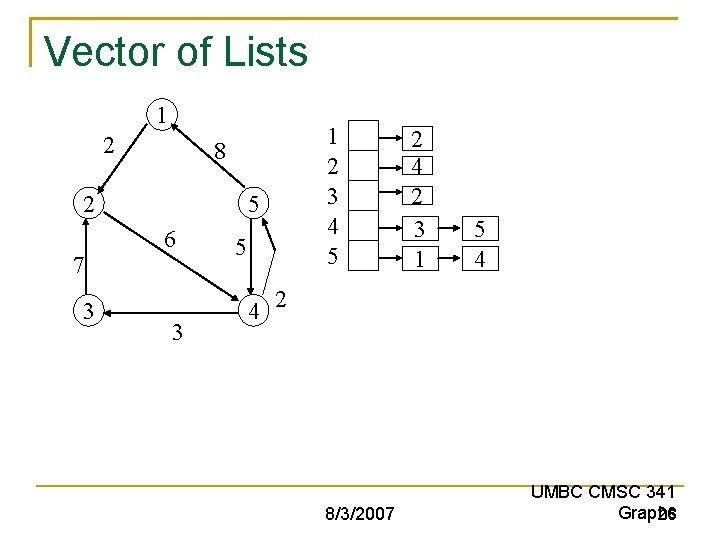
Vector of Lists 1 2 8 2 7 3 1 2 3 4 5 5 6 3 5 4 2 3 1 5 4 2 8/3/2007 UMBC CMSC 341 Graphs 26

Adjacency List Performance Storage requirement: O(|V| + |E|) Performance: O get. Degree( u ) is. Adjacent. To( u, v ) get. Adjacent( u ) 8/3/2007 UMBC CMSC 341 Graphs 27