CMSC 341 Hashing 9162021 1 Hash Table 0

CMSC 341 Hashing 9/16/2021 1

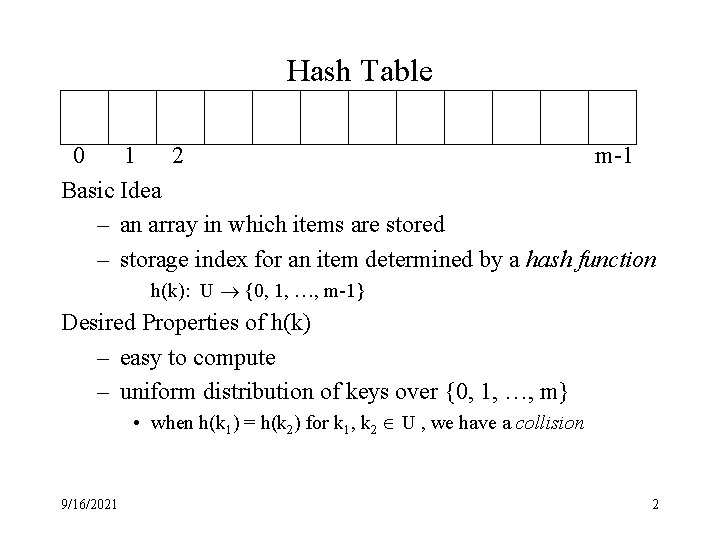
Hash Table 0 1 2 m-1 Basic Idea – an array in which items are stored – storage index for an item determined by a hash function h(k): U {0, 1, …, m-1} Desired Properties of h(k) – easy to compute – uniform distribution of keys over {0, 1, …, m} • when h(k 1) = h(k 2) for k 1, k 2 U , we have a collision 9/16/2021 2

Division Method The function: h(k) = k mod m where m is the table size. m must be chosen to spread keys evenly. – Ex: m = a factor of 10 – Ex: m = 2 b, b> 1 A good choice of m is a prime number. Also we want the table to be no more than 80% full. – Choose m as smallest prime number greater than mmin, where mmin = (expected number of entries)/0. 8 9/16/2021 3

Multiplication Method The function h(k) = m(k. A - k. A ) where A is some real positive constant. A very good choice of A is the inverse of the “golden ratio. ” Given two positive numbers x and y, the ratio x/y is the golden ratio if = x/y = (x+y)/x The golden ratio: x 2 - xy - y 2 = 0 2 - - 1 = 0 = (1 + sqrt(5))/2 = 1. 618033989… ~= Fibi/Fibi-1 9/16/2021 4

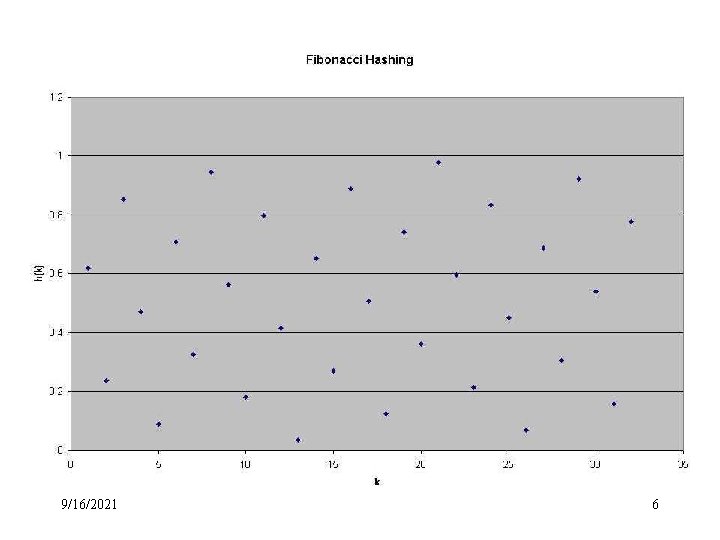
Multiplication Method (cont. ) Because of the relationship of the golden ratio to Fibonacci numbers, this particular value of A in the multiplication method is called “Fibonacci hashing. ” Some values of h(k) = m(k -1 - k -1 ) =0 9/16/2021 for k = 0. 618 m for k = 1 ( -1 = 1/ 1. 618… = 0. 618…) = 0. 236 m for k = 2 = 0. 854 m for k = 3 = 0. 472 m for k = 4 = 0. 090 m for k = 5 = 0. 708 m for k = 6 = 0. 326 m for k = 7 =… = 0. 777 m for k = 32 5

9/16/2021 6

Non-integer Keys In order to has a non-integer key, must first convert to a positive integer: h(k) = g(f(k)) with f: U int g: I {0. . m-1}/2 Suppose the keys are strings. How can we convert a string (or characters) into an integer value? 9/16/2021 7

Horner’s Rule int hash(const string &key, int tablesize) { int hashval = 0; // f(k) by Horner’s rule for (int i = 0; i < key. length(); i++) hashval = 37*hashval + key[i]; // g(k) by division method hashval %= tablesize; if (hashval < 0) hashval += tablesize; return hashval; } 9/16/2021 8

Hash. Table Class template <class Hashed. Obj> class Hash. Table { public: explicit Hash. Table(const Hashed. Obj &not. Found, size=101); Hash. Table(const Hash. Table &rhs) : ITEM_NOT_FOUND(rhs. ITEM_NOT_FOUND), the. Lists(rhs. the. Lists) { /* no code */ } const Hashed. Obj &find(const Hashed. Obj &x) const; void make. Empty(); void insert (const Hashed. Obj &x); void remove (const Hashed. Obj &x); const Hash. Table& operator=(const Hash. Table &rhs); private: vector<List<Hashed. Obj> > the. Lists; const Hashed. Obj ITEM_NOT_FOUND; }; 9/16/2021 9

Hash Table Ops const Hashed. Obj &find(const Hashed. Obj &x) const; – returns the Hashed. Obj in the table, if present – otherwise, returns ITEM_NOT_FOUND void insert (const Hashed. Obj &x); – if x already in table, do nothing. – otherwise insert it, using the appropriate hash function void remove (const Hashed. Obj &x); – remove the instance of x, if x is present – otherwise, does nothing void make. Empty(); 9/16/2021 10

Handling Collisions are inevitable. How to handle them? One possibility: separate chaining (aka open hashing) – store colliding items in a list – if m is large enough, list lengths are small Insertion of key k – hash(k) to find bucket – if k is in that list, do nothing. Else, insert k on that list. Asymptotic performance – if always inserted at head of list, and no duplicates, insert = O(1): best, worst, average 9/16/2021 11

Find Performance Find – hash k to find the bucket – do a find on that list, returns a list. Itr – if itr. is. Past. End(), return ITEM_NOT_FOUND, otherwise, return itr. retrieve() Performance – best: – worst: – average 9/16/2021 12

Remove Performance Remove k from table – hash k to find bucket – remove k from list Performance – best – worst – average 9/16/2021 13

Handling Collisions Revisited Open addressing (aka closed hashing) – all elements stored in the table itself (so table should be large. Rule of thumb: M >= 2 N) – upon collision, item is hashed to a new (open) slot. Hash function h: U x {0, 1, 2, …. } {0, 1, …, M-1} h( k, I ) = (h’ ( k ) + f( I ) ) mod m for some h’: U {0, 1, …, M-1} and f(0) = 0 Each try is called a probe 9/16/2021 14

Linear Probing Function: f(i) = ci Example: h’(k) = k mod 10 in a table of size 10 , f(i) = i U={89, 18, 49, 58, 69} 9/16/2021 15

Linear Probing (cont) Problem: Clustering – when table starts to fill up, performance O(N) Asymptotic Performance – insertion and unsuccessful find, average • # probes (½) (1+1/(1 - )2) • if 1, the denominator goes to zero and the number of probes goes to infinity 9/16/2021 16

Linear Probing (cont) Remove – Can’t just use the hash function(s) to find the object, and remove it, because objects that were inserted after x were hashed based on x’s presence. – Can just mark the cell as deleted so it won’t be found anymore. • Other elements still in right cells • Table can fill with lots of deleted junk 9/16/2021 17

Quadratic Probing Function: f(i) = c 2 i 2 + c 1 i + c 0 Example: f(i) = i 2, m=10 U={89, 18, 49, 58, 69} 9/16/2021 18

Quadratic Probing (cont. ) Advantage: – reduced clustering problem Disadvantages: – reduced number of sequences – no guarantee that empty slot will be found if lambda >= 0. 5 if table size is not prime 9/16/2021 19

Double Hashing Use two hash functions: h’ 1(k), h’ 2(k) h(k, I) = (h’ 1(k) + ih’ 2(k)) mod M Choosing h’ 2(k) – don’t allow h’ 2(k) = 0 for any k. – a good choice: • h’ 2(k) = R - (k mod R) with R a prime smaller than M Characteristics – No clustering problem – Requires a second hash function 9/16/2021 20