CMSC 341 Graphs 2 Weighted Shortest Path Problem

CMSC 341 Graphs 2

Weighted Shortest Path Problem Single-source shortest-path problem: Given as input a weighted graph, G = (V, E), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G. Use Dijkstra’s algorithm – keep tentative distance for each vertex giving shortest path length using vertices visited so far – keep vertex before this vertex (to allow printing of path) – at each step choose the vertex with smallest distance among the unvisited vertices (greedy algorithm) 2

Dijkstra’s Algorithm Vertex v, w; start. dist = 0; for (; ; ) { v = smallest unknown distance vertex; if (v. path == NOT_A_VERTEX) break; v. known = TRUE; for each w adjacent to v if (!w. known) if (v. dist + cvw < w. dist) { decrease (w. dist to v. dist + cvw); w. path = v; } } 3

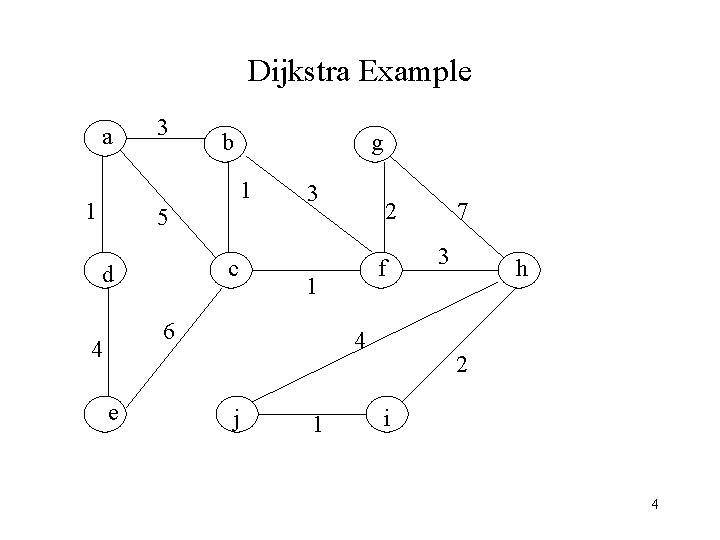
Dijkstra Example a 3 b g 1 1 5 c d 3 e f 1 6 4 2 4 j 1 7 3 h 2 i 4

Edge Types After DFS, edges can be classified into the following types: – tree edges -- a discovered vertex v 1 encounters an undiscovered vertex v 2; the edge between them is a tree edge – back edges -- a discovered vertex v 1 encounters a discovered but unfinished vertex v 2; the edge between them is a back edge. (Graph has a cycle if and only if there is a back edge. ) – forward edges (directed graphs only) -- a discovered vertex v 1 encounters a finished vertex v 2 – cross edges (directed graphs only) -- a discovered vertex v 1 encounters a finished vertex v 2 and d[v 1] > d[v 2] 5

Edge Types (after DFS completion) Condition Type of Edge (v 1, v 2) 6

Traversal Performance What is the performance of DF and BF traversal? Each vertex appears in the stack or queue exactly once. Therefore, the traversals are at least O(|V|). However, at each vertex, we must find the adjacent vertices. Therefore, df- and bf-traversal performance depends on the performance of the get. Adjacent operation. 7

get. Adjacent Method 1: Look at every vertex (except u), asking “are you adjacent to u? ” List L = new List(<class of vertex>); for (each vertex v, except u) if (is. Connected(u, v)) L. do. Insert(v); Assuming O(1) performance on is. Connected, get. Adjacent has O(|V|) performance and traversal performance is O(|V 2|); 8

get. Adjacent (cont) Method 2: Look only at the edges which impinge on u. Therefore, at each vertex, the number of vertices to be looked at is D(u), the degree of the vertex (use outdegree for directed graph). This approach is O(D(u)). The traversal performance is since get. Adjacent is done O(|V|) times. However, in a disconnected graph, we must still look at every vertex, so the performance is O(max(|V|, |E|)) = O(|V| + |E|). But, what is O(|E|) ? ? 9

Number of Edges Theorem: The number of edges in an undirected graph G=(V, E) is O(|V|2) Proof: Suppose G is fully connected. Let p =|V|. We have the following situation: vertex connected to 1 2 … p 2, 3, 4, 5, …, p 1, 2, 3, 4, …, p-1 – There are p(p-1)/2 = O(|V|2) edges. So O(|E|) = O(|V|2). 10